This Packet Belongs to Student Name Topic 8

This Packet Belongs to ____________ (Student Name) Topic 8: Measurement and Modeling in Two and Three Dimensions Unit 7– Measurement and Modeling in Two and Three Dimensions Module 18: Volume Formulas 18. 1 18. 2 18. 3 18. 4 Volume of Prisms and Cylinders Volume of Pyramids Volumes of Cones Volume of Spheres Module 19: Visualizing Solids 19. 1 Cross-Sections and Solids of Rotation 19. 2 Surface Area of Prisms and Cylinders 19. 3 Surface Area of Pyramids and Cones 19. 4 Surface Area of Spheres Module 20: Modeling and Problem Solving 20. 1 Scale Factors 20. 2 Modeling and Density 20. 3 Problem Solving with Constraints 1

Quick Access to Module Lesson. Click on desired Lesson 2

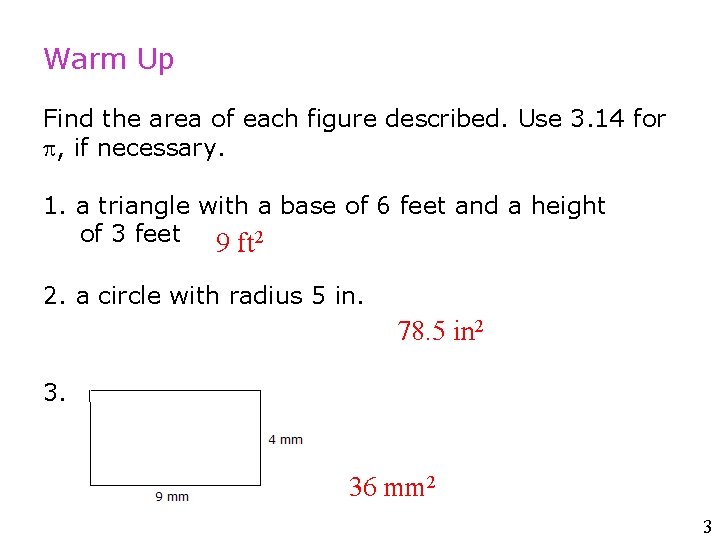
10 -2 Volume of Prisms and Cylinders Warm Up Find the area of each figure described. Use 3. 14 for , if necessary. 1. a triangle with a base of 6 feet and a height of 3 feet 9 ft 2 2. a circle with radius 5 in. 78. 5 in 2 3. 36 mm 2 Holt CA Course 1 3

Module 18 VOLUME FORMULAS Objectives Use formulas routinely for finding the perimeter and area of basic prisms, pyramids, cylinders, cones, and spheres. Vocabulary: Volume, right vs oblique Assignments: REGULAR HONORS (Pg 932)18. 1 #’s 2, 4, 16, 21 (5 questions) (Pg 943)18. 2 #’s 1, 2, 5 -7 odd, 12, 21, 22 (7 questions) (Pg 955)18. 3 #’s 2 -4, 11, 23 (6 questions) (Pg 967)18. 4 #’s 3 -7 odd, 12 (4 questions) (Pg 932)18. 1 #’s 4 -8 even, 21 (4) (Pg 943)18. 2 #’s 2, 5 -7 odd, 21, 22 (5) (Pg 955)18. 3 #’s 2 -4 even, 11 (3) (Pg 967)18. 4 #’s 3 -7 odd, 12 (4) 4

Volume • The volume of a three-dimensional figure is the number of cubes it can hold. Each cube represents a unit of measure called a cubic unit. 5

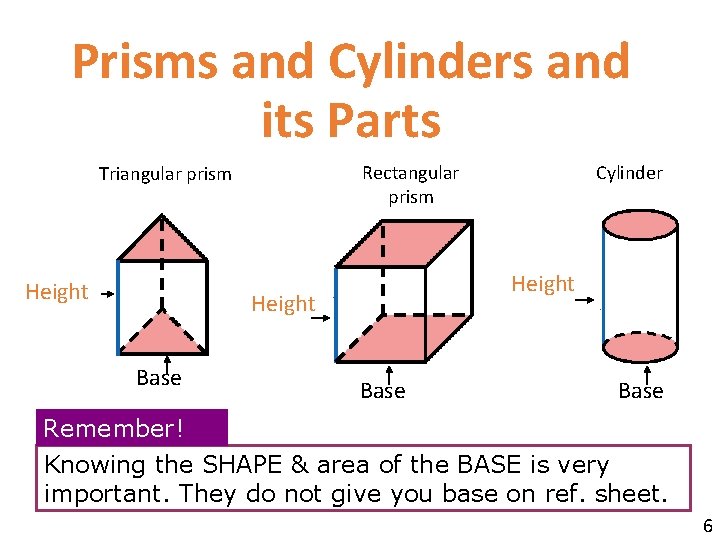
Prisms and Cylinders and its Parts Rectangular prism Triangular prism Height Base Cylinder Base Remember! Knowing the SHAPE & area of the BASE is very important. They do not give you base on ref. sheet. 6

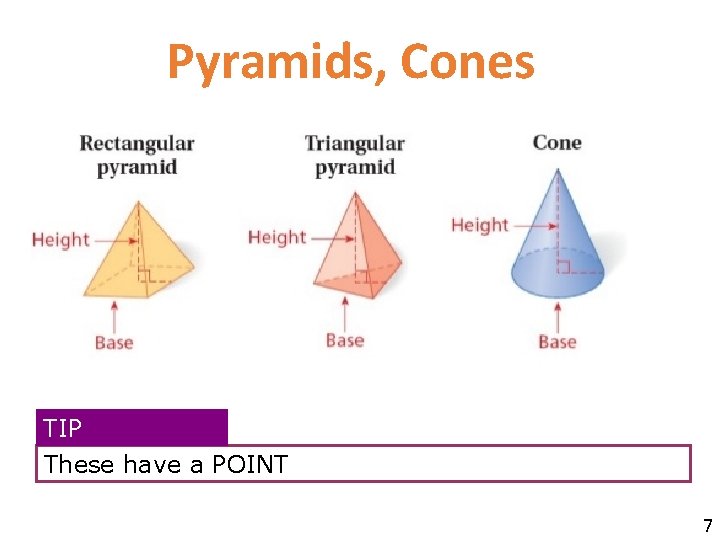
Pyramids, Cones TIP These have a POINT 7

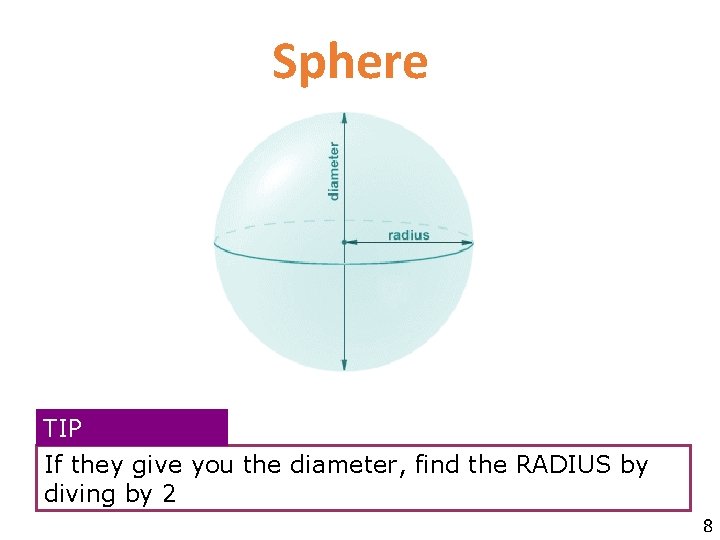
Sphere TIP If they give you the diameter, find the RADIUS by diving by 2 8

General Formula for Prism • AREAS of BASES If BASE is Rectangle/Square If BASE is Triangle If BASE is Circle What if they give you diameter? 10

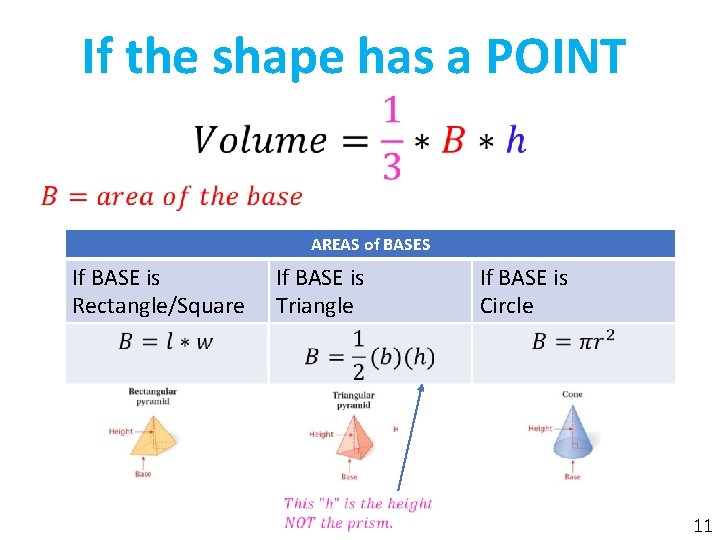
If the shape has a POINT • AREAS of BASES If BASE is Rectangle/Square If BASE is Triangle If BASE is Circle 11

Volume of a Sphere TIP! Plug in 3. 14 for PI 12

Class Activity • Identify the NAME of the figure • • • Prism (triangular or rectangular) Cylinder Pyramid ((triangular or rectangular) Sphere Cone • Give the Formula of the shape. 13

Cone 14

Rectangular Pyramid 15

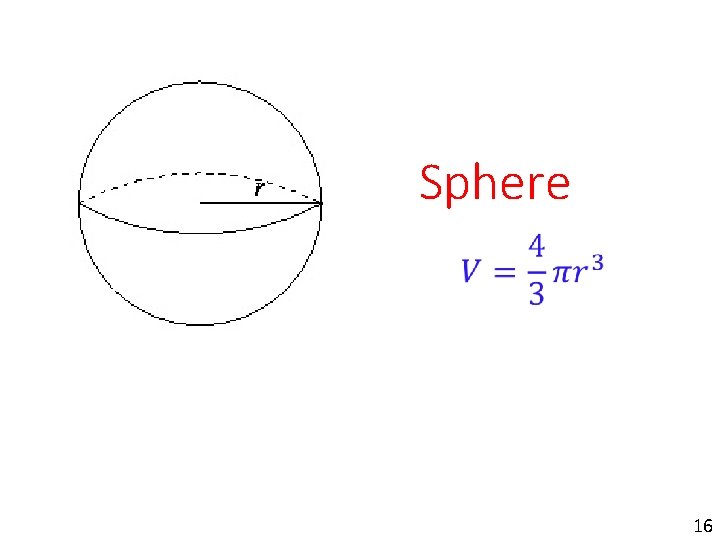
Sphere 16

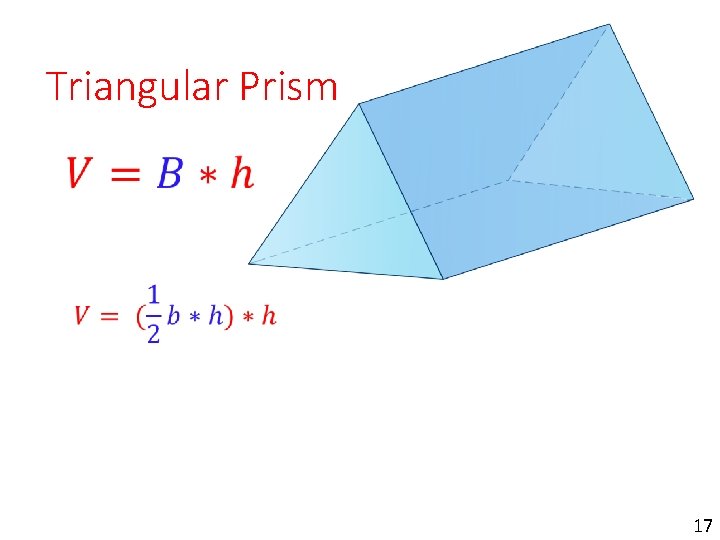
Triangular Prism 17

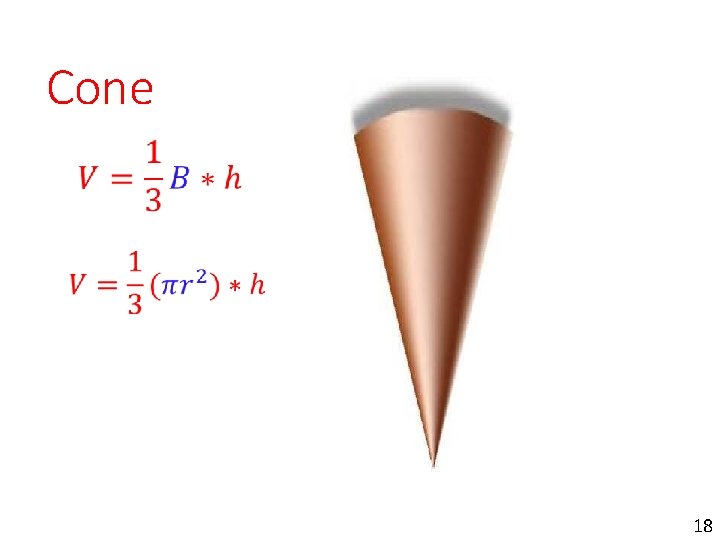
Cone 18

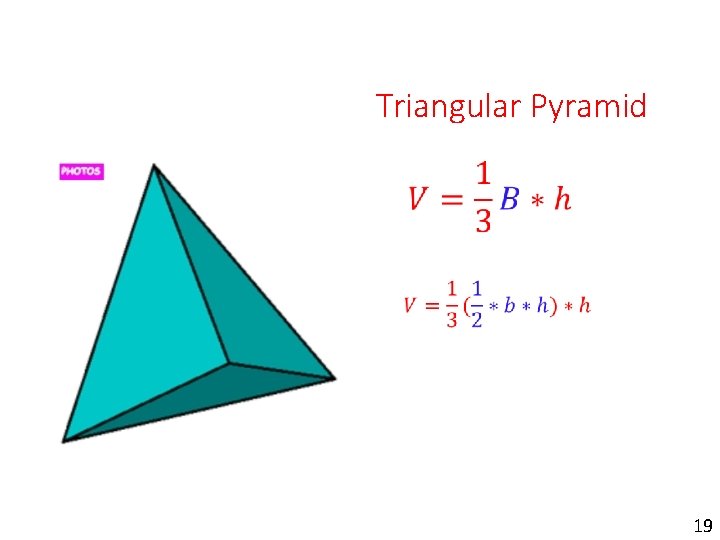
Triangular Pyramid 19

Cylinder

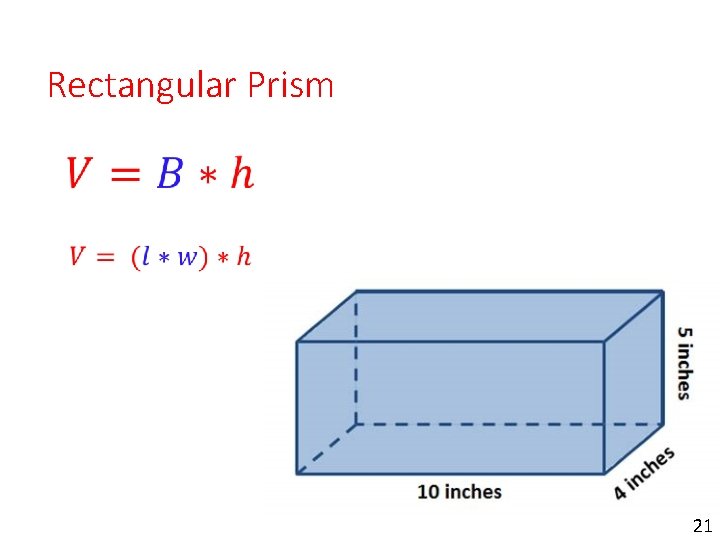
Rectangular Prism 21

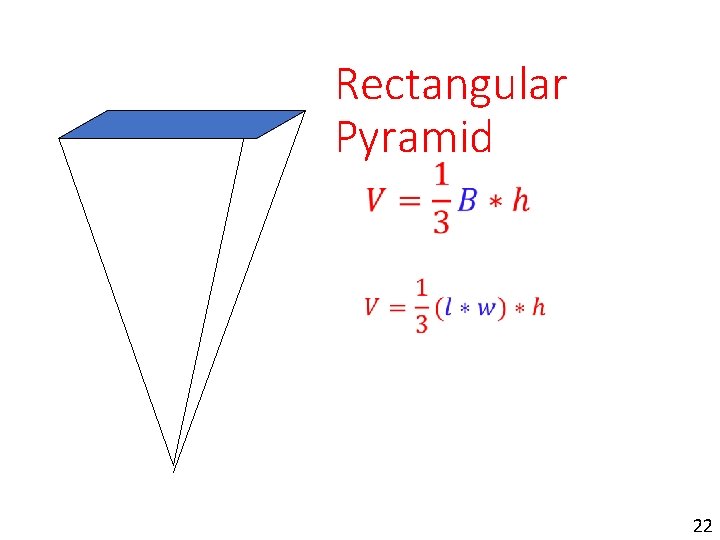
Rectangular Pyramid 22

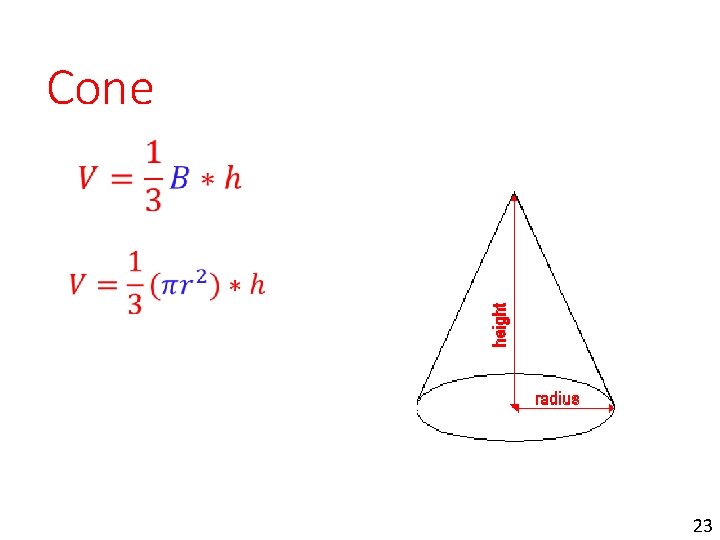
Cone 23

Rectangular Pyram 24

Sphere 25

Warm Up Multiply. Round to nearest hundredth 1. (2 ft)(3. 14)(5 ft)(10 ft) 2. (5. 5 in)(1/2 in)(3. 14) 314 ft 3 8. 64 in 2 26

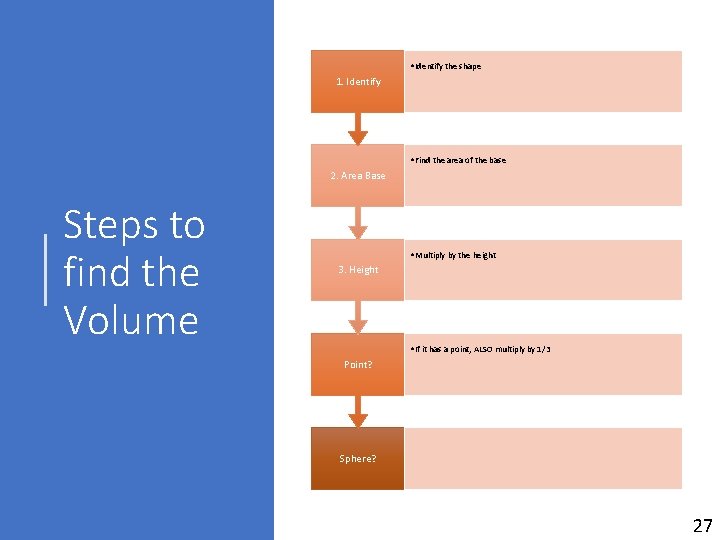
• Identify the shape 1. Identify • Find the area of the base 2. Area Base Steps to find the Volume • Multiply by the height 3. Height • If it has a point, ALSO multiply by 1/3 Point? Sphere? 27

Example 1 A: Finding the Volume of Prisms Find the volume of each figure to the nearest tenth. A. 1. Identify Shape Rectangular Prism Does it have a point? V = Bh B = 4 • 12 = 48 ft 2 2. Find Area of Base What is the Base? A rectangle V= 48 • 4 3. Multiply by Height V= 192 ft 3 4. Does it have a point? No. SO you’re done. 28

Example 1 B: Finding the Volume of a Cylinders Find the volume of the figure to the nearest tenth. Use 3. 14 for . B. 1. Identify Shape 2. Find Area of Base Cylinder What is the Base? A circle Does it have a point? B = (r 2) V = Bh B = (42) = 16 in 2 3. Multiply by Height = 16 • 12 in 4. Does it have a point? No. SO you’re done. = 192 602. 9 in 3 29

Example 1 C: Finding the Volume of Prisms Find the volume of the figure to the nearest tenth. Use 3. 14 for . 1. Identify Shape Triangular prism 2. Find Area of Base Does it have a point? V = Bh What is the Base? A triangle 3. Multiply by Height V = 15 • 7 7 ft 4. Does it have a point? No. SO you’re done. V= 105 ft 3 30

Example 3 C: Finding Volumes of Cones Find the volume of a cone. Step 1 Use the Pythagorean Theorem to find the height. 162 + h 2 = 342 h 2 = 900 h = 30 Pythagorean Theorem Subtract 162 from both sides. Take the square root of both sides. Step 2 Use the radius and height to find the volume. Volume of a cone Substitute 16 for r and 30 for h. 2560 cm 3 8042. 5 cm 3 Simplify. 31

Example 1 D: Finding the Volume of Pyramids Find the volume of the figure to the nearest tenth. Use 3. 14 for . 1. Identify Shape Rectangular Pyramid Does it have a point? 2. Find Area of Base What is the Base? A rectangle 3. Multiply by Height = 64 • 9 4. Does it have a point? 32

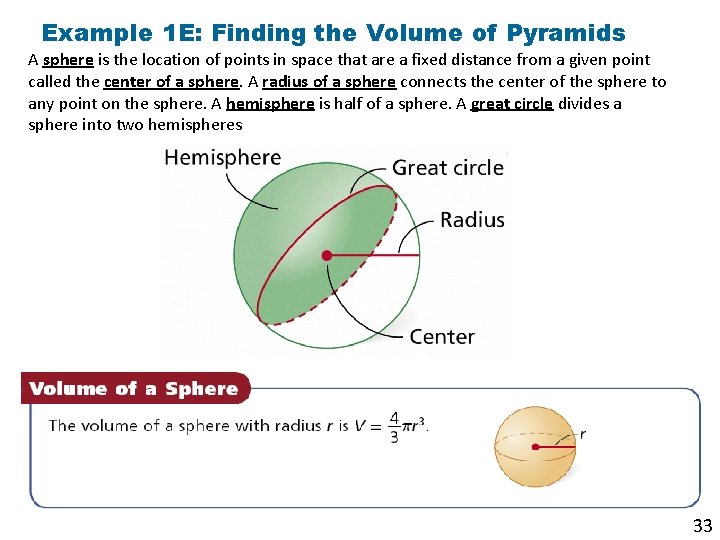
Example 1 E: Finding the Volume of Pyramids A sphere is the location of points in space that are a fixed distance from a given point called the center of a sphere. A radius of a sphere connects the center of the sphere to any point on the sphere. A hemisphere is half of a sphere. A great circle divides a sphere into two hemispheres 33

1 E. Sphere– Volume Find the volume of the sphere. Give your answer in terms of . Volume of a sphere. 12 for r. = 2304 in 3 Simplify. 34

2 E. Sphere– Diameter via Volume Find the diameter of a sphere with volume 36, 000 cm 3. Volume of a sphere. Substitute 36, 000 for V. 27, 000 = r 3 r = 30 d = 60 cm Take the cube root of both sides. d = 2 r 35

3 E. Sphere– Volume Find the volume of the hemisphere. Volume of a hemisphere Substitute 15 for r. = 2250 m 3 Simplify. 36

YOUR TURN Find the volume of the figure to the nearest tenth. Use 3. 14 for . A. 10 in. 6 in. 3 in. B = 6 • 3 = 18 in. 2 The base is a rectangle. V = Bh Volume of prism = 18 • 10 Substitute for B and h. = 180 in 3 Multiply. 37

YOUR TURN Find the volume of the figure to the nearest tenth. Use 3. 14 for . B. B = (82) The base is a circle. = 64 cm 2 8 cm Volume of a V = Bh cylinder 15 cm Substitute for B = (64 )(15) = 960 and h. 3, 014. 4 cm 3 Multiply. 38

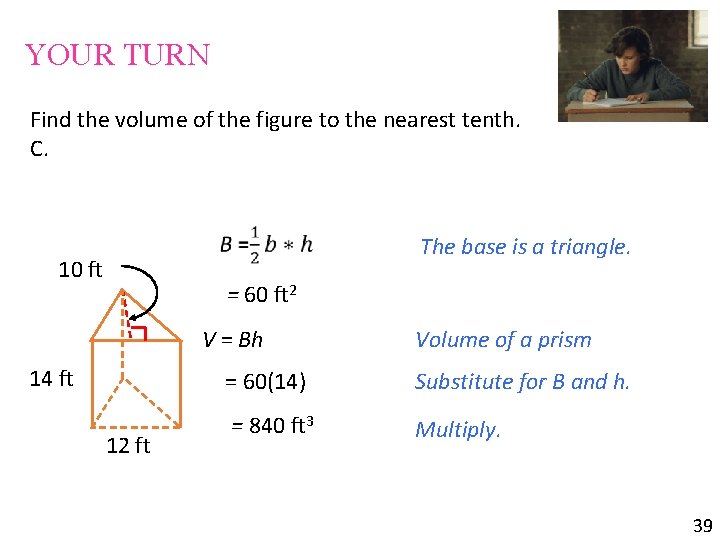
YOUR TURN Find the volume of the figure to the nearest tenth. C. 10 ft The base is a triangle. = 60 ft 2 V = Bh 14 ft = 60(14) 12 ft = 840 ft 3 Volume of a prism Substitute for B and h. Multiply. 39

Your Turn! Example E Find the Volume of the sphere. 2. Find the radius of a sphere with volume 2304 ft 3. Volume of a sphere Substitute for V. r = 12 ft Simplify. 40

41

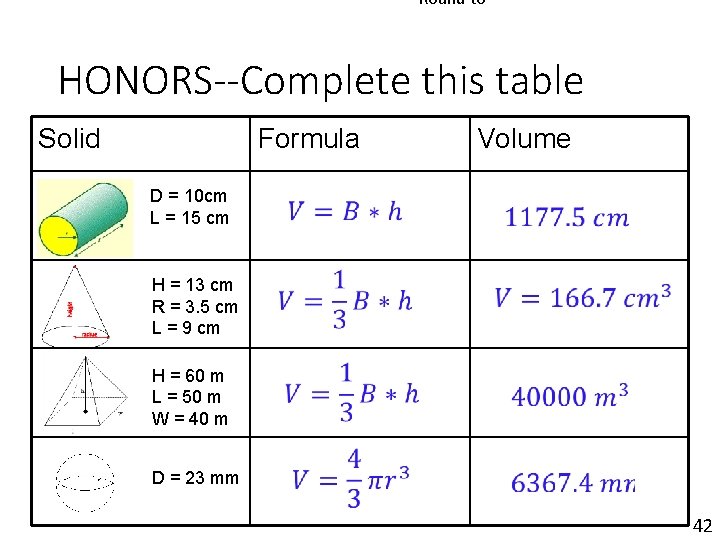
Round to HONORS--Complete this table Solid Formula D = 10 cm L = 15 cm H = 13 cm R = 3. 5 cm L = 9 cm H = 60 m L = 50 m W = 40 m D = 23 mm Volume 42

Additional Example 2: Music Application A drum company advertises a snare drum that is 4 inches high and 12 inches in diameter. Estimate the volume of the drum. 1. Identify Shape & Parts 3. Multiply by Height Cylinder V = Bh d = 12, h = 4 r=6 2. Find Area of Base What is the Base? Circle B = r 2 B = (6)2 (use 3. 14 for pi) 4. Does it have a point? No. SO you’re done. The volume of the drum is approximately 452 in 3. 43

YOUR TURN A drum company advertises a bass drum that is 12 inches high and 28 inches in diameter. Estimate the volume of the drum. d = 28, h = 12 r = 14 B = ( r 2) BASE is area of circle V = ( r 2)h = (3. 14)(14)2 • 12 Multiply by height Use 3. 14 for . = (3. 14)(196)(12) = 7385. 28 ≈ 7, 385 The volume of the drum is approximately 7, 385 in 3. 44

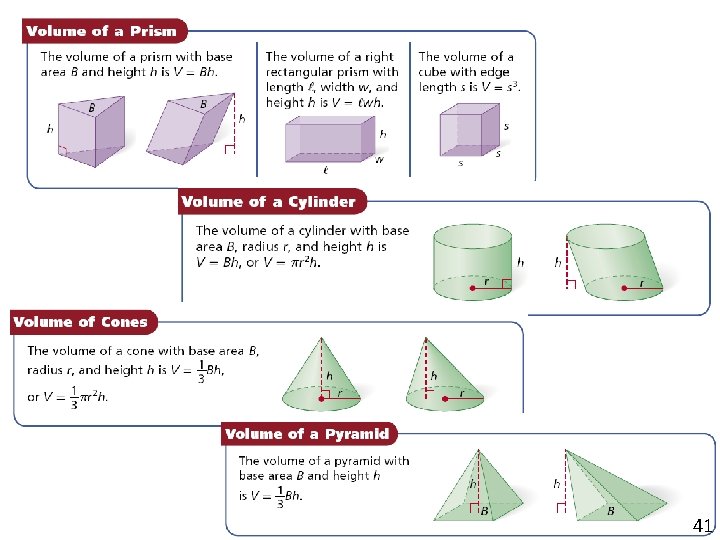
Volume Formulas Prisms and Cylinders Cube: V = x 3 Rectangular Prism: V = lwh or V = Bh Triangular Prism: V = Bh Cylinder: V = � r 2 h or V = Bh **Basically, V = Bh for any Prism or Cylinder 45

Classwork/Homework Volume HONORS (Pg 932)18. 1 #’s 2, 4, 16, 21 (5 questions) (Pg 943)18. 2 #’s 1, 2, 5 -7 odd, 12, 21, 22 (7 questions) (Pg 955)18. 3 #’s 2 -4, 11, 23 (6 questions) (Pg 967)18. 4 #’s 3 -7 odd, 12 (4 questions) REGULAR (Pg 932)18. 1 #’s 2, 4, 21 (3 questions) (Pg 943)18. 2 #’s 2, 5 -7 odd, 21, 22 (5 questions) (Pg 955)18. 3 #’s 2 -4 even, 11 (3 questions) (Pg 967)18. 4 #’s 3 -7 odd, 12 (4 questions) Click Here for LESSON QUIZ 46

Mod 18: Area of Composite figures Objectives Apply and combine the volume formulas routinely composite figures Vocabulary: Composite figures Assignments: HONORS (Pg 932)18. 1 #9, 10, 19 (3) (Pg 943)18. 2 #’s 8, 9, 18, 19 (4) (Pg 955)18. 3 #’s 7, 8, 12 (3) (Pg 967)18. 4 #’s 10, 13, 14* (3) REGULAR (Pg 932)18. 1 #9, 10, 19 (3 questions) (Pg 943)18. 2 #’s 8, 9, (2 questions) (Pg 955)18. 3 #’s 7, 8, 12 (3 questions) (Pg 967)18. 4 #’s 10, 13, (2 questions) 47

Composite Figures • A composite figure is a figure that is made up of two or more geometric figures It could be two volumes ADDED It could be two volumes SUBTRACTED OR 48

Example 4 A: Finding the Volume of Composite Figures Find the volume of the barn. Volume of barn = Volume of rectangular prism + Volume of triangular prism = 30, 000 + 10, 000 = 40, 000 ft 3 The volume of the barn is 40, 000 ft 3. 49

Example 4 B: Finding Volumes of Composite Three-Dimensional Figures Find the volume of the composite figure. Round to the nearest tenth. The volume of the rectangular prism is: V = ℓwh = (8)(4)(5) = 160 cm 3 The base area of the regular triangular prism is: The volume of the regular triangular prism is: An equilateral Triangle? Think 30 -60 -90 special Right triangle The total volume of the figure is the sum of the volumes. 50

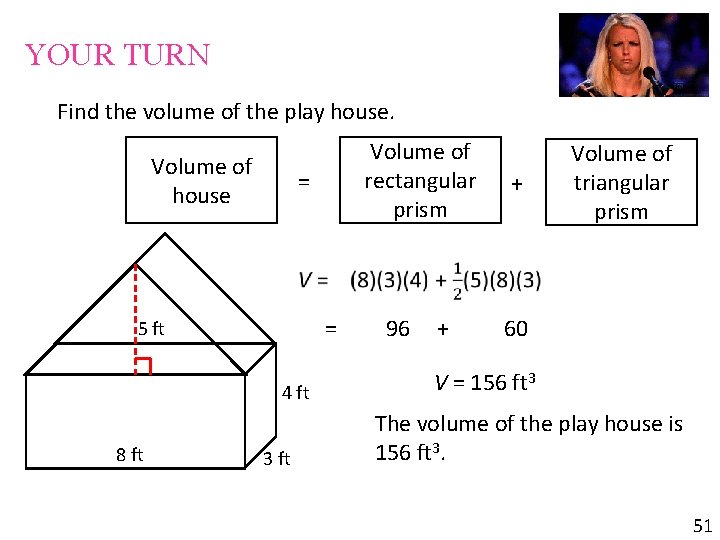
YOUR TURN Find the volume of the play house. Volume of house = Volume of rectangular prism + Volume of triangular prism = 96 + 60 5 ft 4 ft 8 ft 3 ft V = 156 ft 3 The volume of the play house is 156 ft 3. 51

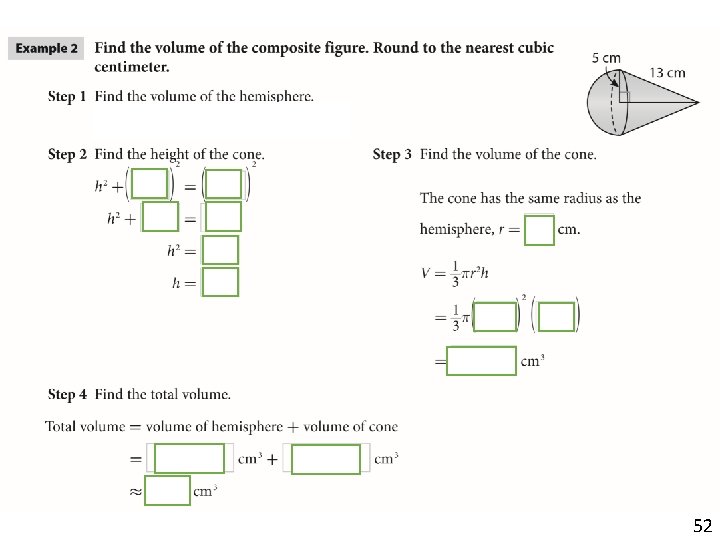
Composite Figure a cone in a cone or what not. 52

53

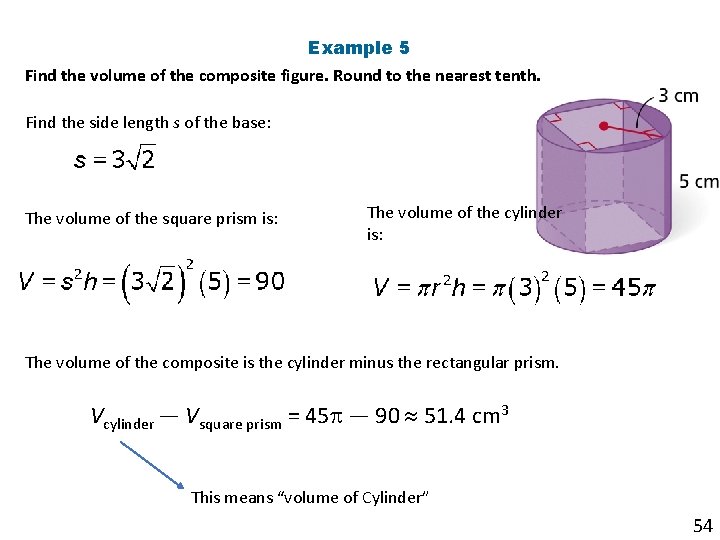
Example 5 Find the volume of the composite figure. Round to the nearest tenth. Find the side length s of the base: The volume of the square prism is: The volume of the cylinder is: The volume of the composite is the cylinder minus the rectangular prism. Vcylinder — Vsquare prism = 45 — 90 51. 4 cm 3 This means “volume of Cylinder” 54

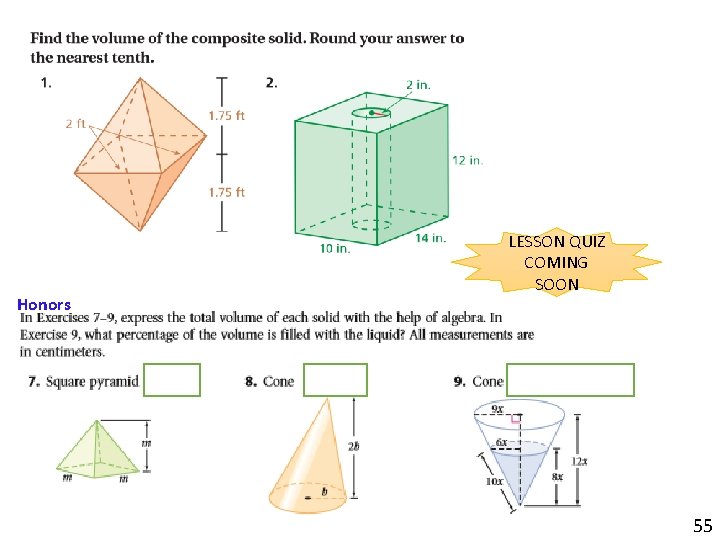
1529. 2 in 3 4. 7 ft 3 Honors LESSON QUIZ COMING SOON 55

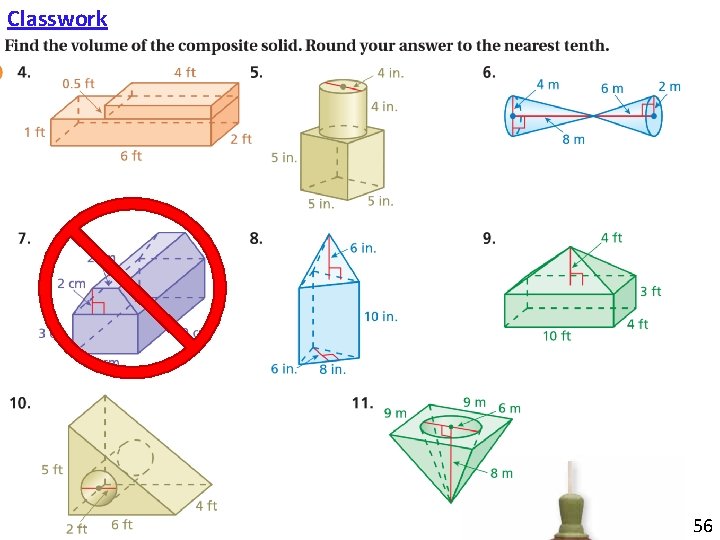
Classwork 56

Classwork/Homework Volume of Composite Figures HONORS (Pg 932)18. 1 #9, 10, 19 (3 questions) (Pg 943)18. 2 #’s 8, 9, 18, 19 (4 questions) (Pg 955)18. 3 #’s 7, 8, 12 (3 questions) (Pg 967)18. 4 #’s 10, 13, 14* (3 questions) REGULAR (Pg 932)18. 1 #9, 10, 19 (3 questions) (Pg 943)18. 2 #’s 8, 9, (2 questions) (Pg 955)18. 3 #’s 7, 8, 12 (3 questions) (Pg 967)18. 4 #’s 10, 13, (2 questions) Click Here for LESSON QUIZ 57

19. 1 Cross Sections & 3 d figures Objectives Identify cross sections of 3 D figures Draw the Vocabulary: • Cross section Assignments: HONOR #1 -9 odd, 12 -18 even (9) REGULAR (Pg 986)19. 1 #3 -9 odd, 14 -18 EVEN (7) 58

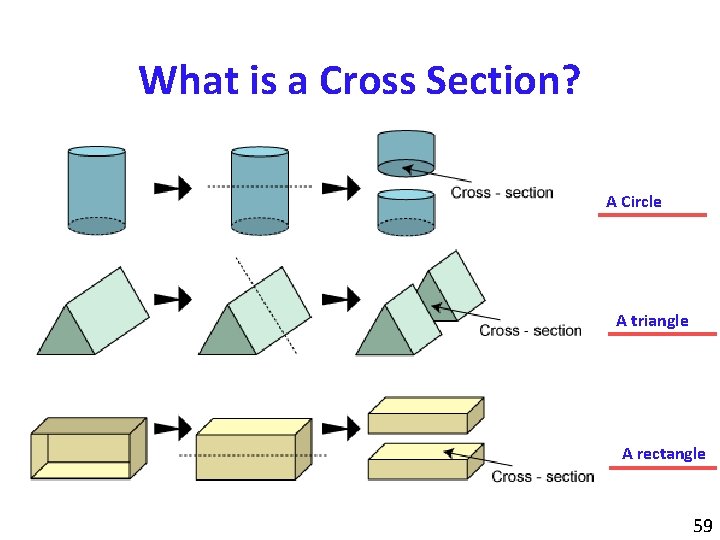
What is a Cross Section? A Circle A triangle A rectangle 59

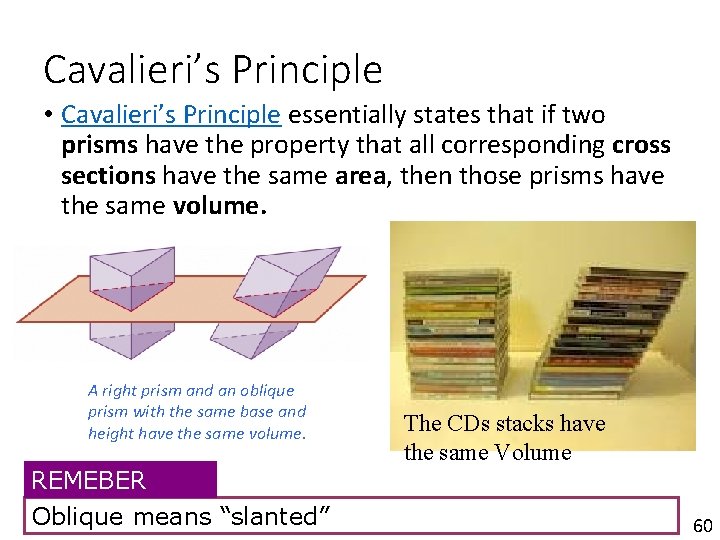
Cavalieri’s Principle • Cavalieri’s Principle essentially states that if two prisms have the property that all corresponding cross sections have the same area, then those prisms have the same volume. A right prism and an oblique prism with the same base and height have the same volume. REMEBER Oblique means “slanted” The CDs stacks have the same Volume 60

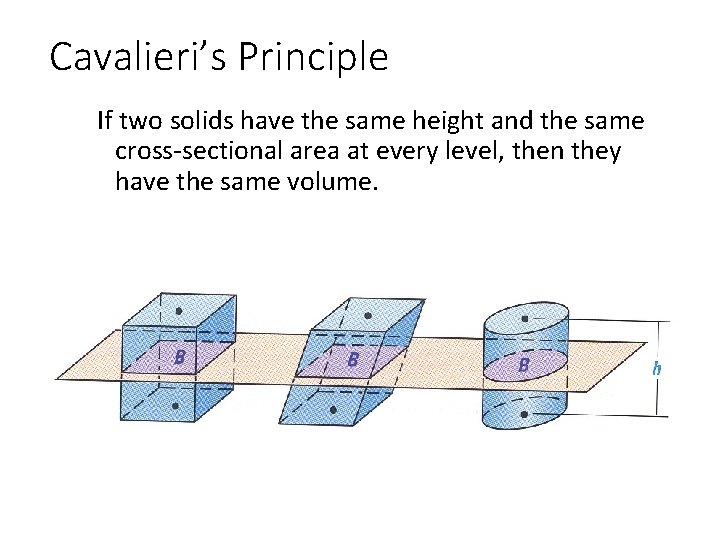
Cavalieri’s Principle If two solids have the same height and the same cross-sectional area at every level, then they have the same volume.

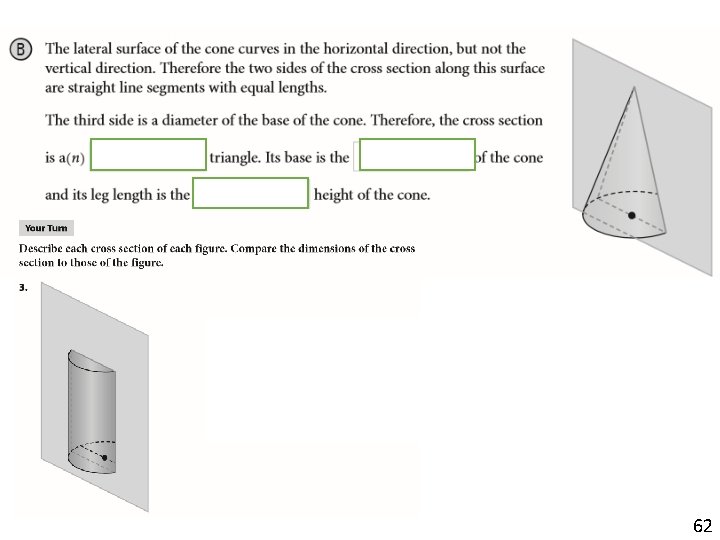
62

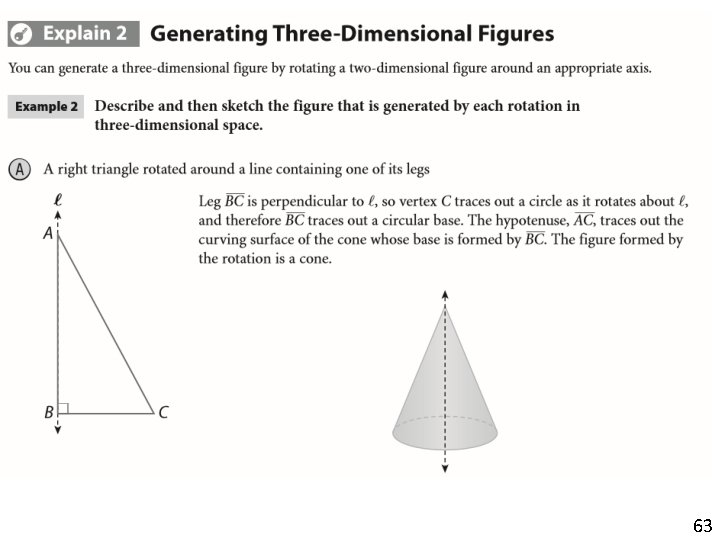
63

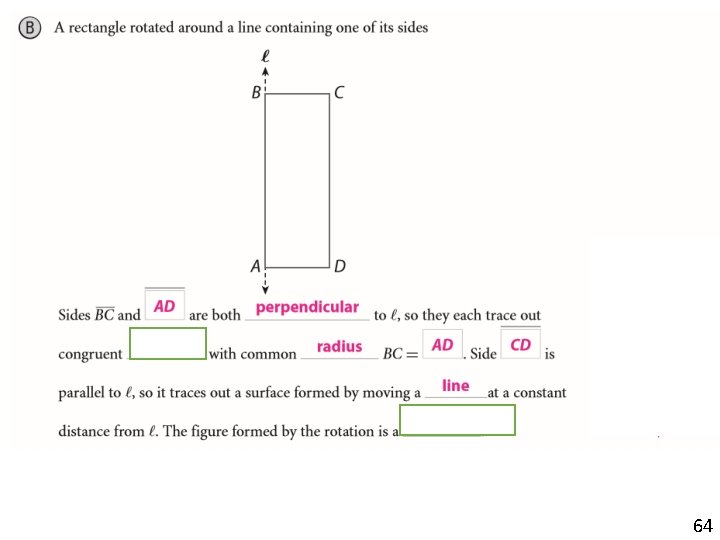
64

65

Classwork/Homework HONORS (Pg 986)19. 1 #1 -9 odd, 12 -18 even (9 questions) REGULAR (Pg 986)19. 1 #3 -9 odd, 14 -18 EVEN (6 questions) 66

Warm Up Find the perimeter and area of each polygon. 1. a rectangle with base 14 cm and height 9 cm P = 46 cm; A = 126 cm 2 2. a right triangle with 9 cm and 12 cm legs. P = 36 cm; A = 54 cm 2 3. an equilateral triangle with side length 6 cm 67

Module 19: Surface area Objectives Learn and apply the formula for the surface area of a prism, cylinder, pyramid, cones, and spheres Vocabulary: Base, lateral faces, perimeter Assignments: HONORS (Pg 999)19. 2 # 2, 5, 7 12, 14*, 15, 18, (7 questions) (Pg 1012)19. 3 #’s 5, 8 -9, 12, 13, 21* (6 questions) (Pg 1023)19. 4 #’s 2, 3, 4, 8, 14, 15, 17* (7 questions) REGULAR (Pg 999)19. 2 # 2, 7 12, 18, (4 questions) (Pg 1012)19. 3 #’s 5, 8 -9, 12, (4 questions) (Pg 1023)19. 4 #’s 3, 4, 8, 15 (4 questions) 68

Surface Area of Prisms & Cylinders. 69

Surface Area • The surface area of each of these solids is the sum of the areas of all the faces or surfaces that enclose the solid. For prisms and pyramids, the faces include the solid’s bases and its lateral faces. • How will the answer be labeled? • Units 2 because it is area! 70

Let’s start in the beginning… Before you can do surface area or volume, you have to know the following formulas. Rectangle Triangle Circle A = lw A = ½ bh A = π r² Steps for Finding Surface Area 1. Draw and label each face of the solid as if you had cut the solid apart along its edges and laid it flat. Label the dimensions. 2. Calculate the area of each face. If some faces are identical, you only need to find the area of one. 3. Find the total area of all the faces 71

What is a Geometric Net? http: //www. mathsisfun. com/definitions/net. html 72

A. Rectangular Prism – Surface Area 1. Draw and label the two congruent bases, and the four lateral faces unfolded into one rectangle. Then find the areas of all the rectangular faces. 2. Find individual areas and add 73

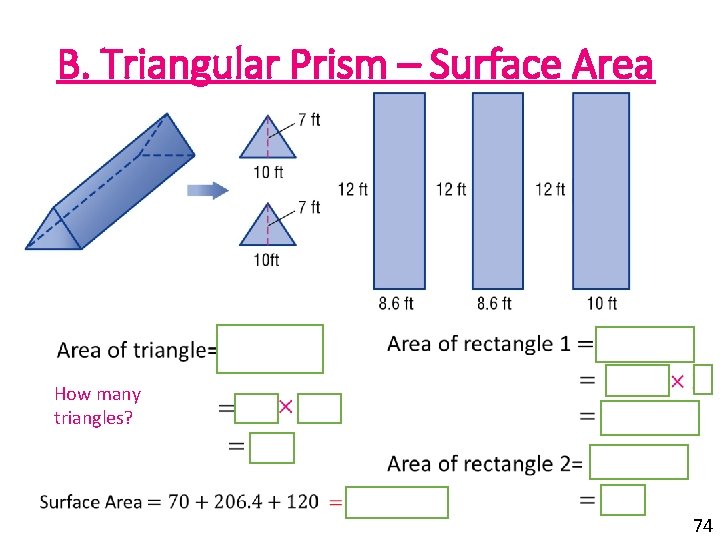
B. Triangular Prism – Surface Area How many triangles? 74

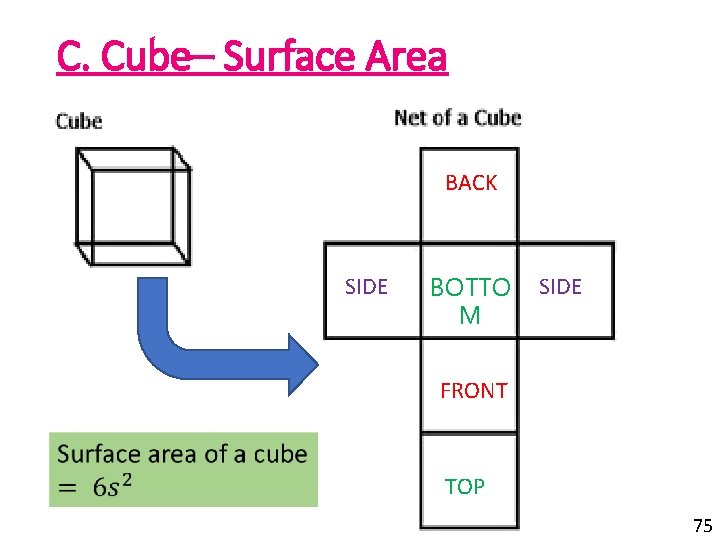
C. Cube– Surface Area BACK SIDE BOTTO M SIDE FRONT TOP 75

D. Cylinder– Surface Area Find the lateral area and surface area of the right cylinder. Give your answers in terms of . The radius is half the diameter, or 8 ft. Top Base Bottom Base Middle What parts make-up a cylinder? 10 76

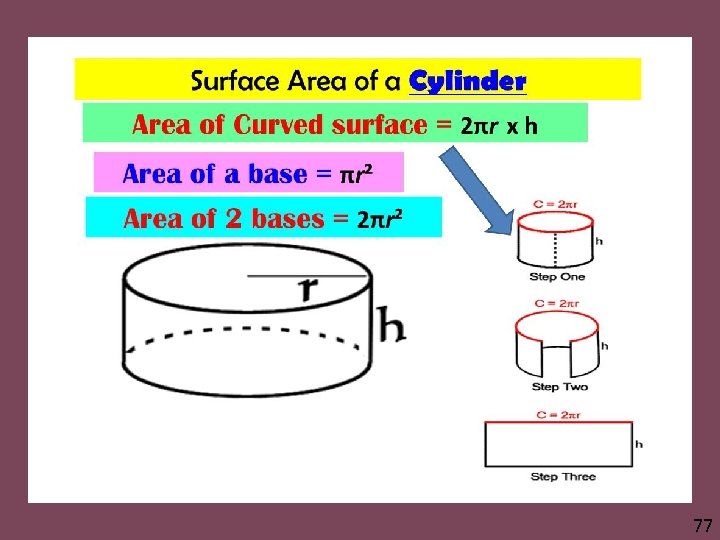
77

Surface Area general • You can find the SA of any prism by using the basic formula for SA which is • L + 2 B= SA • L= lateral Surface area • L= perimeter of the base x height of the prism • B = Area of the base SA=(Lateral Area) +2(Base Area) SA= (Base Perimeter)*height+2(Area of Base) 78

The steps to SA of Prisms 1. 2. 3. 4. 5. 6. What is the base? Find perimeter of the BASE Multiply the perimeter by the height Find the area of the BASE Multiply area of BASE by 2 Add steps 3 and 5 together. 79

General SA Formula Example SA= (Base Perimeter)*height+2(Area of Base) L = Ph P = 2(9) + 2(7) = 32 ft = 32(14) = 448 ft 2 S = Ph + 2 B = 448 + 2(7)(9) = 574 ft 2 Tip! The surface area of a right rectangular prism with length ℓ, width w, and height h can be written as S = 2ℓw + 2 wh + 2ℓh. 80

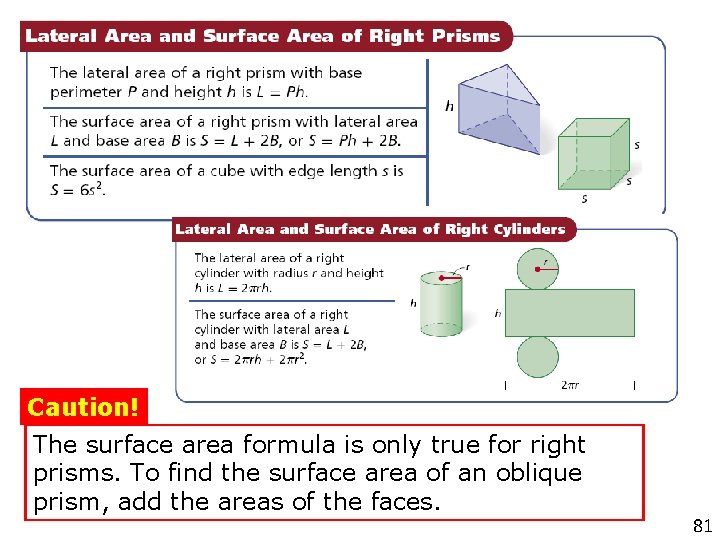
Caution! The surface area formula is only true for right prisms. To find the surface area of an oblique prism, add the areas of the faces. 81

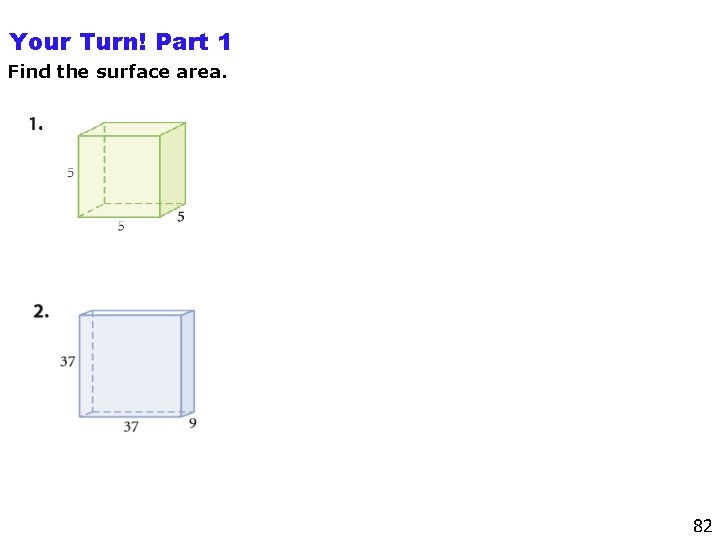
Your Turn! Part 1 Find the surface area. 82

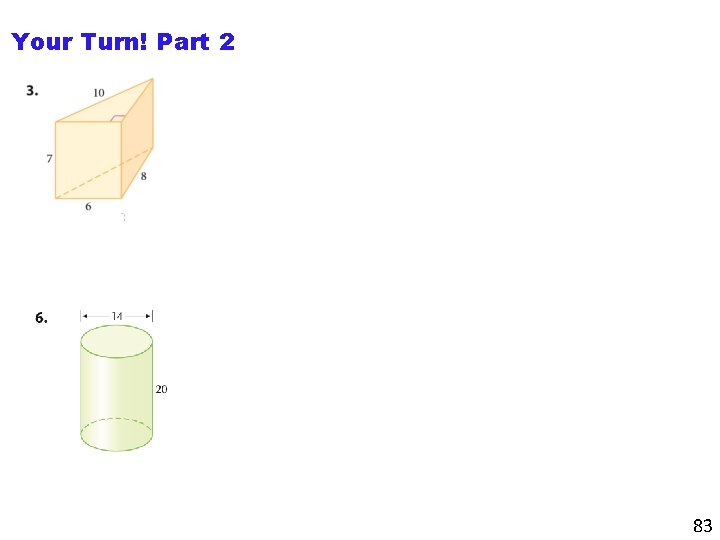
Your Turn! Part 2 83

Surface Area of Spheres 84

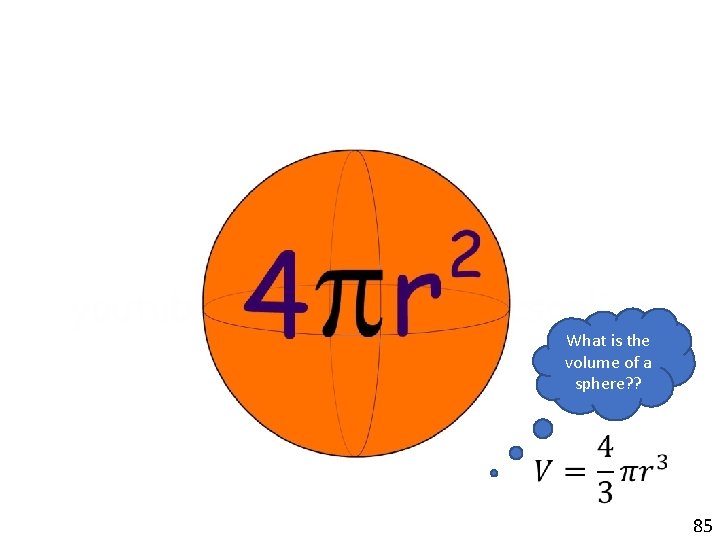
Surface Area of a Sphere What is the volume of a sphere? ? 85

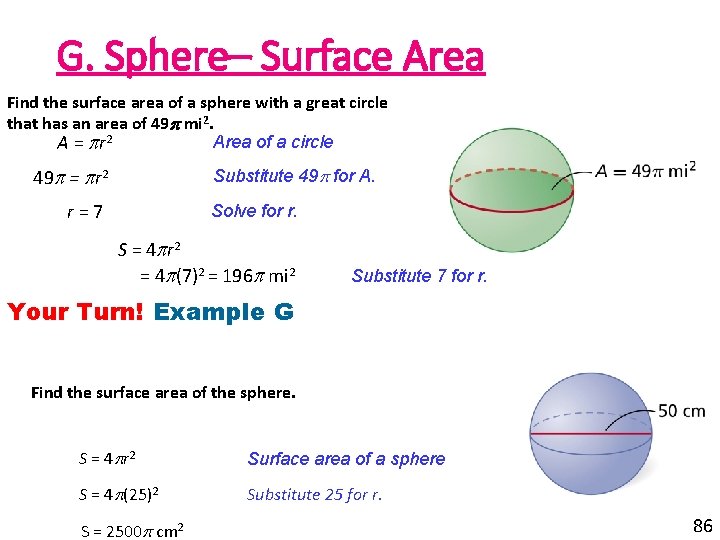
G. Sphere– Surface Area Find the surface area of a sphere with a great circle that has an area of 49 mi 2. Area of a circle A = r 2 49 = r 2 Substitute 49 for A. r = 7 Solve for r. S = 4 r 2 = 4 (7)2 = 196 mi 2 Substitute 7 for r. Your Turn! Example G Find the surface area of the sphere. S = 4 r 2 Surface area of a sphere S = 4 (25)2 Substitute 25 for r. S = 2500 cm 2 86

Surface Area of Pyramids, Cones & Spheres 87

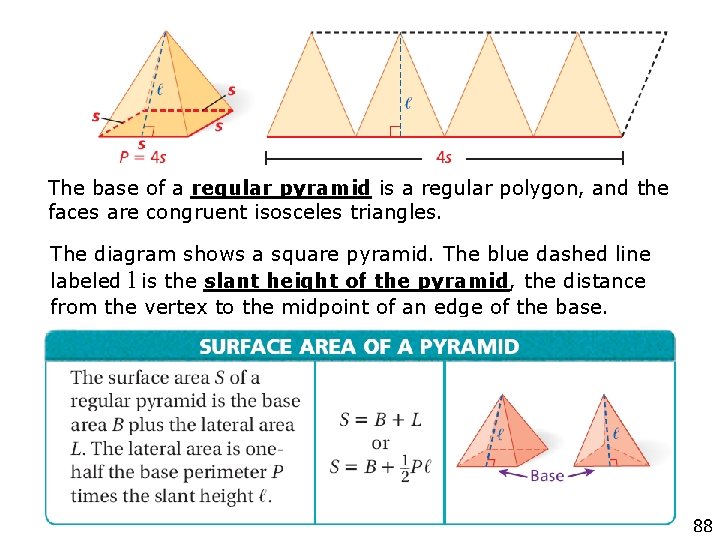
The base of a regular pyramid is a regular polygon, and the faces are congruent isosceles triangles. The diagram shows a square pyramid. The blue dashed line labeled l is the slant height of the pyramid, the distance from the vertex to the midpoint of an edge of the base. 88

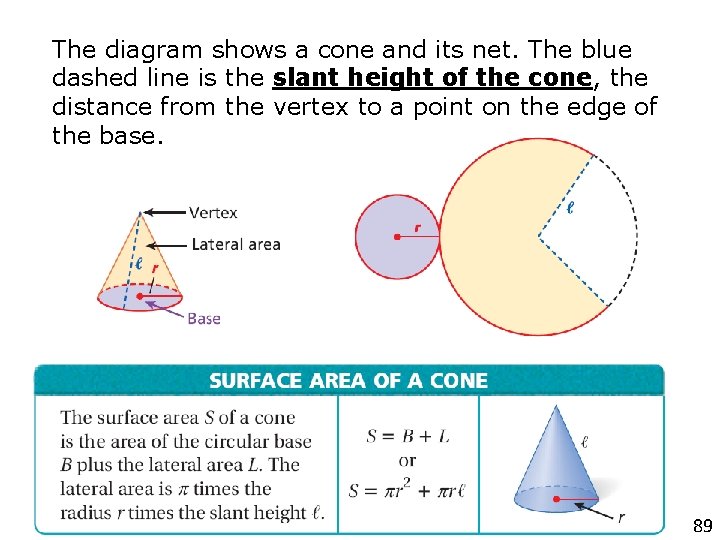
The diagram shows a cone and its net. The blue dashed line is the slant height of the cone, the distance from the vertex to a point on the edge of the base. 89

E. Right Pyramid– Surface Area Find the surface area of the pyramid. S=B+ 1 Pl 2 1 S = lw + Pl 2 S = (9 • 9) + S = 81 + 180 Use the formula. B = lw 1 (36)(10) 2 Substitute. = 4(9) = 36 P Add. S = 261 m 2 The surface area is 261 square meters. 90

F. Right Cone– Surface Area Find the surface area of the cone. Use 3. 14 for . S = r 2 + rl Use the formula. S ≈ (3. 14)(32) + (3. 14)(3)(10) Substitute. S ≈ 28. 26 + 94. 2 Multiply. S ≈ 122. 46 Add. The surface area is about 122. 46 square centimeters. 91

Your Turn! Find the surface area of each pyramid. 1 S = B + 1 Pℓ =(7)(7) + (28)(12) 2 2 S = 49 + 168 = 217 mm 2 Find the surface area of the cone. Use 3. 14 for . S = r 2 + rℓ ≈ 3. 14(2)2 + 3. 14 (2)(8) S ≈ 12. 56 + 50. 24 S ≈ 62. 8 ft 2 92

Warm Up Find the perimeter or circumference of each figure. Use 3. 14 for . 1. 2. 30 cm 138. 16 ft 93

Surface area of Composite Figures 94

Example 1: Finding Surface Areas of Composite Three-Dimensional Figures Find the surface area of the composite figure. The surface area of the rectangular prism is A right triangular prism is added to the rectangular prism. The surface area of the triangular prism is Two copies of the rectangular prism base are removed. The area of the base is B = 2(4) = 8 cm 2. 95

Example 1 Continued The surface area of the composite figure is the sum of the areas of all surfaces on the exterior of the figure. S = (rectangular prism surface area) + (triangular prism surface area) – 2(rectangular prism base area) S = 52 + 36 – 2(8) = 72 cm 2 96

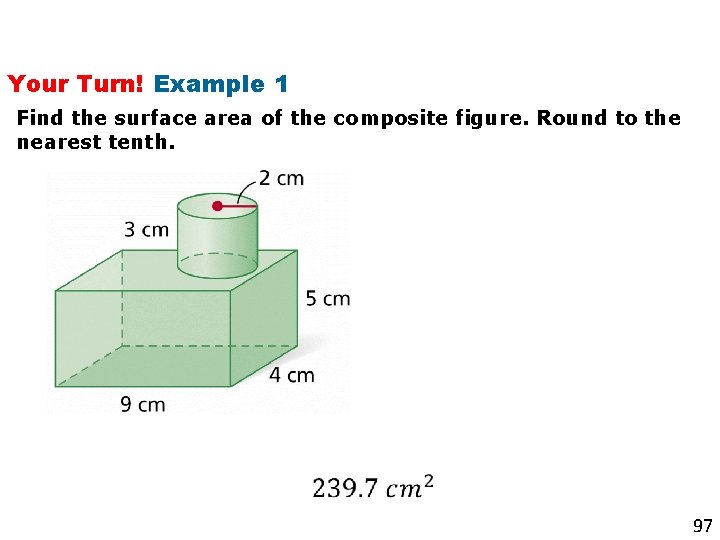
Your Turn! Example 1 Find the surface area of the composite figure. Round to the nearest tenth. 97

Example 2: Recreation Application A sporting goods company sells tents in two styles, shown below. The sides and floor of each tent are made of nylon. Which tent requires less nylon to manufacture? Pup tent: Tunnel tent: The tunnel tent requires less nylon. 98

Classwork/Homework Surface Area HONORS (Pg 999)19. 2 # 2, 5, 7 12, 14*, 15, 18, (7 questions) (Pg 1012)19. 3 #’s 5, 8 -9, 12, 13, 21* (6 questions) (Pg 1023)19. 4 #’s 2, 3, 4, 8, 14, 15, 17* (7 questions) REGULAR (Pg 999)19. 2 # 2, 7 12, 18, (4 questions) (Pg 1012)19. 3 #’s 5, 8 -9, 12, (4 questions) (Pg 1023)19. 4 #’s 3, 4, 8, 15 (4 questions) Click Here for LESSON QUIZ 101

Objectives Explore the effects of volume and surface area by changing the scale factor Vocabulary: Scale factor Assignments: HONORS 20. 1 # 5 -12, 13, 14, 22* 23* Page 944 #11, 17 (13 questions) REGULAR # 6 -12 even, 13, 14, Page 944 #11, 17 (8 questions) 102

Finding the Scale Factor • We can apply a multiplicative factor to any formula (perimeter, circumference, volume, and surface area) • Way 1: • Way 2: Plug in the multiplicator factor directly to the variable from the original formula and compare the final product to the original formula. 103

Ratio • A ratio is a comparison of two quantities

Scale • A scale is a ratio between two sets of measurements. • Examples: • Drawings: ¼ inch = 1 foot • Maps: 1 inch = 250 miles

Scale Drawing (Model) • A scale drawing (model) is a drawing that uses a scale to make an object smaller than (reduction) or larger than (enlargement) the real object.

Scale Factor • A scale factor is a ratio used to enlarge or reduce similar figures. • Examples: enlarging a piece of candy for a drawing…or the Willy Wonka Factory…

The lengths and widths of objects of a scale drawing or model are proportional to the lengths and widths of the actual object.

1. A set of landscape plans shows a flower bed that is 6. 5 inches wide. The scale on the plans is 1 inch = 4 feet. a. What is the width of the actual flower bed? 26 feet b. What is the scale factor? 1/48

2. The central chamber of the Lincoln memorial, which features a marble statue of Abraham Lincoln, has a height of 60 feet. Suppose a scale model of the chamber has a height of 4 inches. What is the scale of the model? a. Write a ratio of the height of the model to the actual height of the statue? 60 ft 15 ft 4 in 1 inch = 15 feet b. What is the scale factor? 1/180

3. Antonio is designing a room that is 20 feet long and 12 feet wide. Make a scale drawing of the room. Use the scale 0. 25 inches = 4 feet. STEP 1: Find the room’s length on the drawing (let x = length) 20 x = 4 Length = 1. 25 inches . 25 STEP 2: Find the room’s width on the drawing (let w = width) 12 x = 4. 25 Width =. 75 inches

Practice Problems: Pgs. 1043 -1044 #s 5 -17 ALL

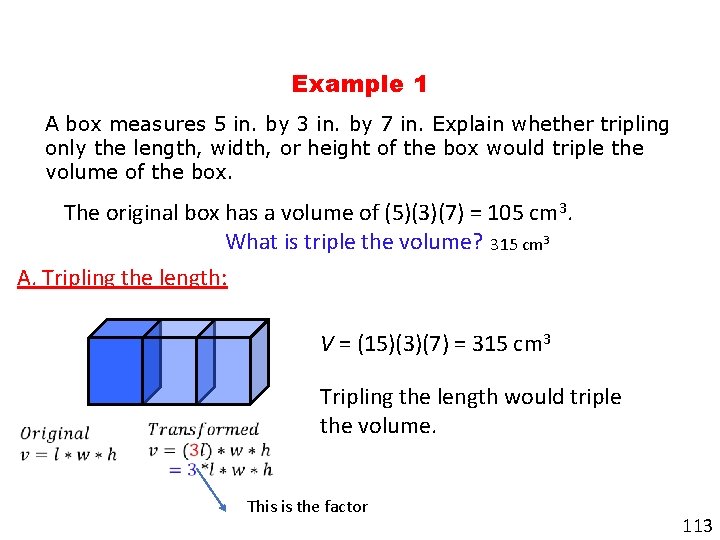
Example 1 A box measures 5 in. by 3 in. by 7 in. Explain whether tripling only the length, width, or height of the box would triple the volume of the box. The original box has a volume of (5)(3)(7) = 105 cm 3. What is triple the volume? 315 cm 3 A. Tripling the length: V = (15)(3)(7) = 315 cm 3 Tripling the length would triple the volume. This is the factor 113

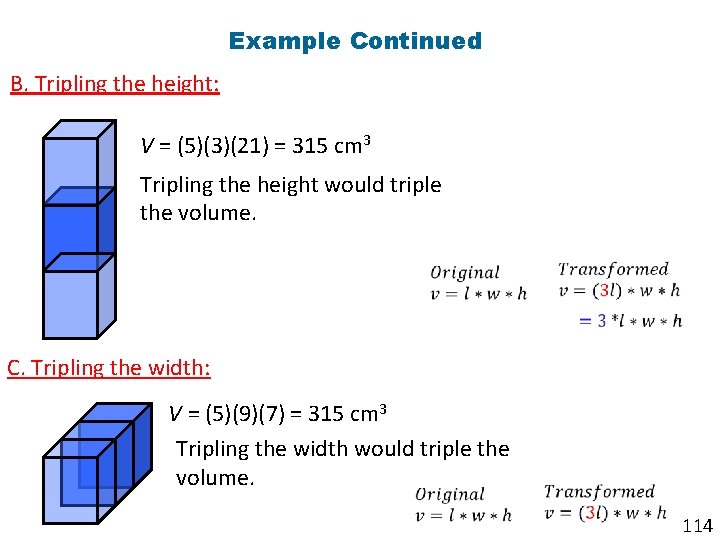
Example Continued B. Tripling the height: V = (5)(3)(21) = 315 cm 3 Tripling the height would triple the volume. C. Tripling the width: V = (5)(9)(7) = 315 cm 3 Tripling the width would triple the volume. 114

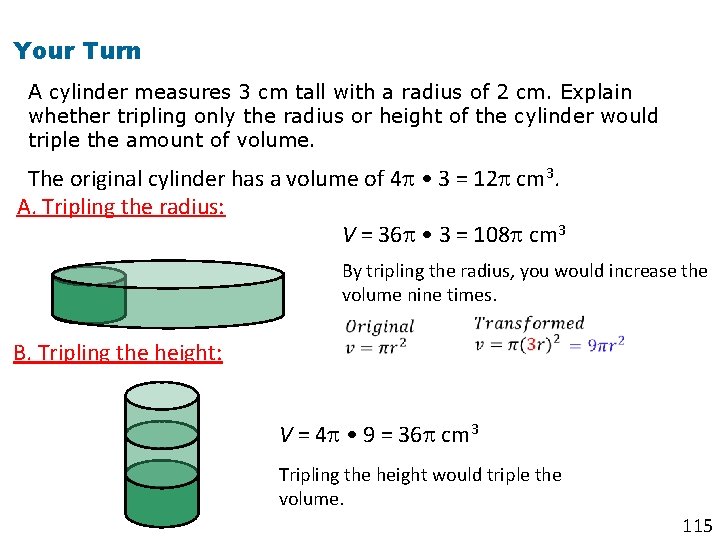
Your Turn A cylinder measures 3 cm tall with a radius of 2 cm. Explain whether tripling only the radius or height of the cylinder would triple the amount of volume. The original cylinder has a volume of 4 • 3 = 12 cm 3. A. Tripling the radius: V = 36 • 3 = 108 cm 3 By tripling the radius, you would increase the volume nine times. B. Tripling the height: V = 4 • 9 = 36 cm 3 Tripling the height would triple the volume. 115

Example 3: Exploring Effects of Changing Dimensions original dimensions: 116

Example 2: Sports Application A sporting goods store sells exercise balls in two sizes, standard (22 -in. diameter) and jumbo (34 -in. diameter). How many times as great is the volume of a jumbo ball as the volume of a standard ball? jumbo ball: standard ball: =3. 7 A jumbo ball is about 3. 7 times as great in volume as a standard ball. 117

Classwork/Homework Scale Factor Effects HONORS (Pg 1043) 20. 1 # 5 -12, 13, 14, 22* 23* Page 944 #11, 17 (13 questions) REGULAR (Pg 1043) 20. 1 # 6 -12 even, 13, 14, Page 944 #11, 17 (8 questions) 123

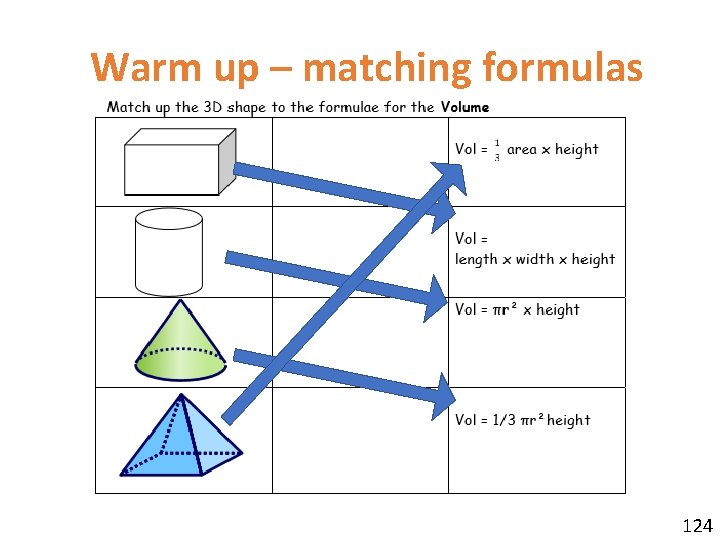
Warm up – matching formulas 124

Objectives Apply concepts of density based on area and volume in modeling situations. Vocabulary: Density, population density, BTU’s Assignments: HONORS REGULAR 20. 2 # 1, 2, 3, 4, 5, 7, 10, 12, 16 (9 questions) 20. 2 # 1, 2, 4, 5, 7, 12, (6 questions) 20. 3 # 5, 8, 14, 16 -17, 20*, 22* (7 questions) 20. 3 # 5, 8, 14, 16 -17 (5 questions) 125

• What is Density? 126

Additional Example 1: Recreational Application A swimming pool is a rectangular prism. Estimate the volume of water in the pool in gallons when it is completely full (Hint: 1 gallon ≈ 0. 134 ft 3). The density of water is about 8. 33 pounds per gallon. Estimate the weight of the water in pounds. Step 1 Find the volume of the swimming pool in cubic feet. V = ℓwh = (25)(15)(9) = 3375 ft 3 127

Example 3 Continued A swimming pool is a rectangular prism. Estimate the volume of water in the pool in gallons when it is completely full (Hint: 1 gallon ≈ 0. 134 ft 3). The density of water is about 8. 33 pounds per gallon. Estimate the weight of the water in pounds. 209, 804 pounds The swimming pool holds about 25, 187 gallons. The water in the swimming pool weighs about 209, 804 pounds. 128

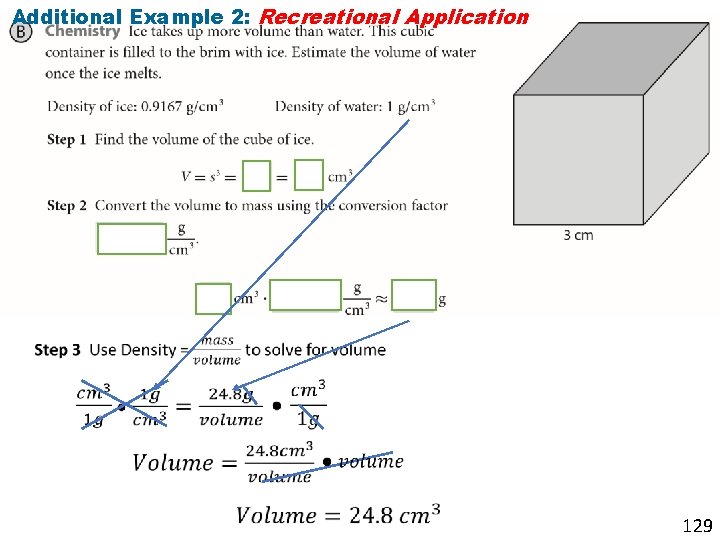
Additional Example 2: Recreational Application 129

Additional Example 3: Recreational Application 130

131

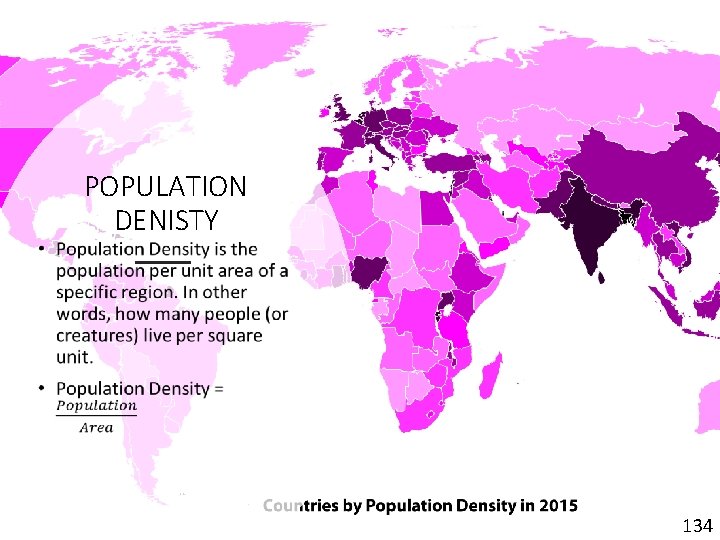
• POPULATION DENISTY 134

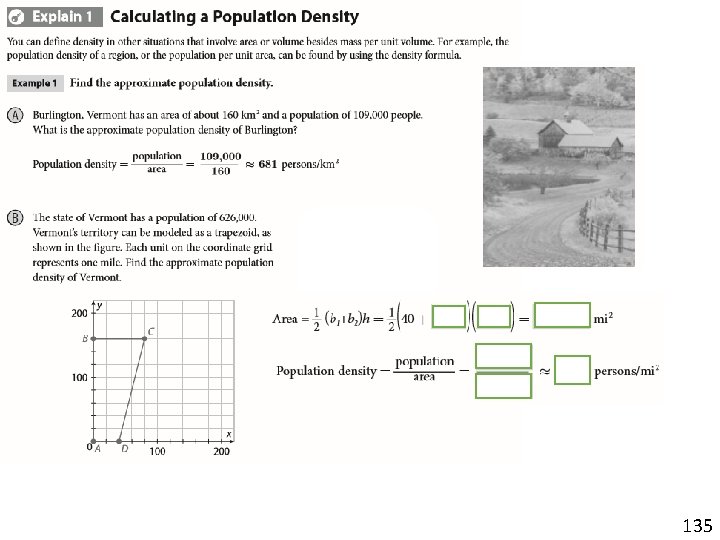
135

136

MEASURES OF ENERGY • 137

138

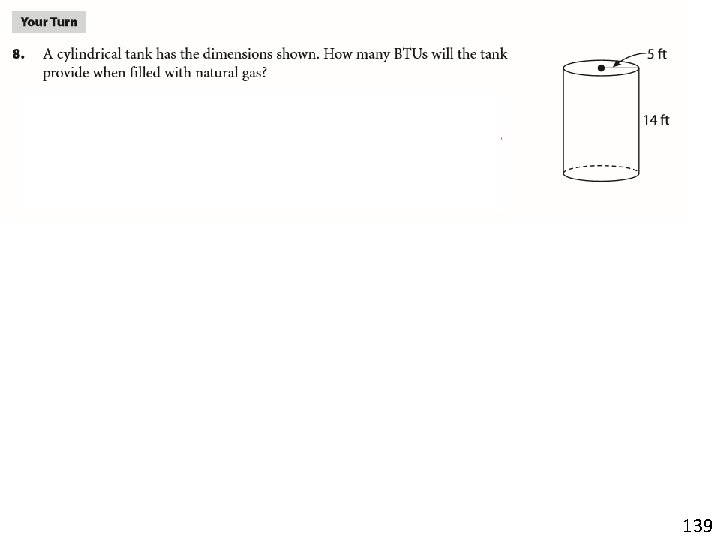
139

Classwork/Homework Density & Modeling HONORS (Pg 1051)20. 2 # 1, 2, 3, 4, 5, 7, 10, 12, 16 (9 questions) REGULAR (Pg 1051)20. 2 # 1, 2, 4, 5, 7, 12, (6 questions) 144

Starting 20. 3 What is a constraint? Constraints give you a value to be substituted into an equation relating a dimension to a volume or surface area, allowing the equation to be solved, and the dimensions found. 145

146

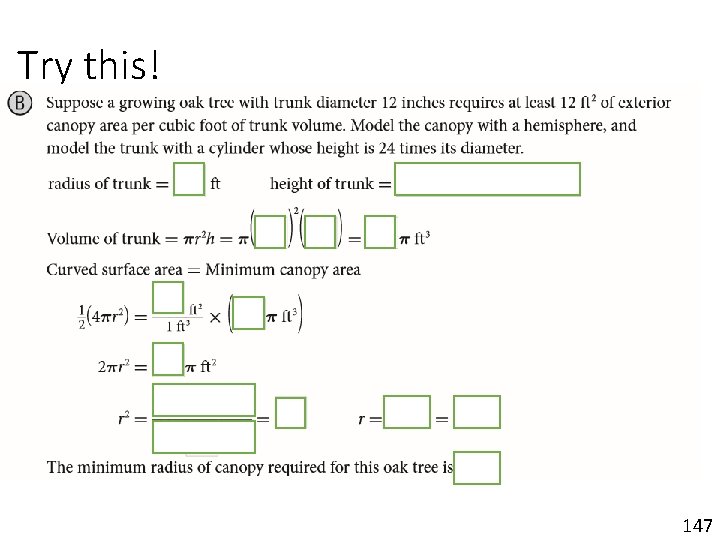
Try this! 147

Determining dimensions given a volume 148

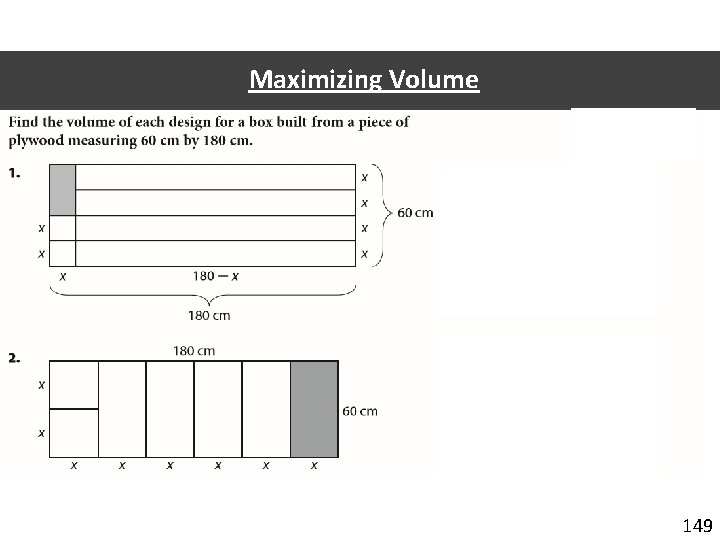
Maximizing Volume 149

Classwork/Homework Constraints HONORS (Pg 1063)20. 3 # 5, 8, 14, 16 -17, 20*, 22* (7 questions) REGULAR (Pg 1063)20. 3 # 5, 8, 14, 16 -17 (5 questions) 150