Chapter 2 Signals and Spectra All sections except































- Slides: 49

Chapter 2 Signals and Spectra (All sections, except Section 8, are covered. )

Physically Realizable Waveform 1. Non zero over finite duration (finite energy) 2. Non zero over finite frequency range (physical limitation of media) 3. Continuous in time (finite bandwidth) 4. Finite peak value (physical limitation of equipment) 5. Real valued (must be observable)

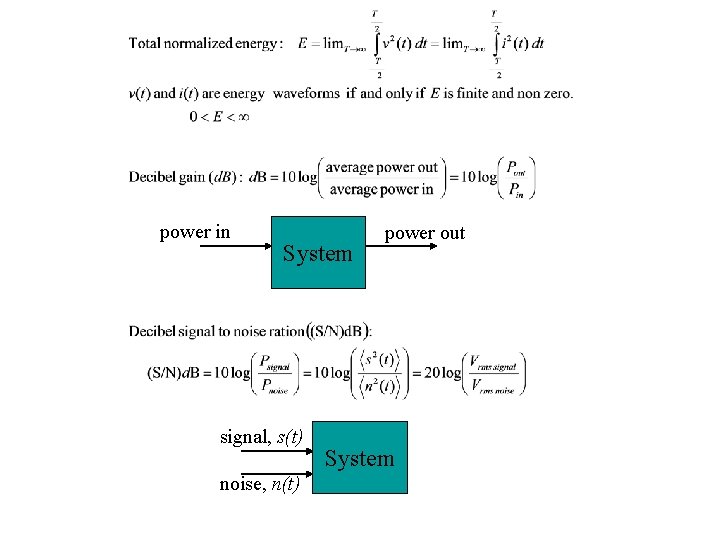
• Power Signal: finite power, infinite energy • Energy Signal: finite energy, non-zero power over limited time • All physical signals are energy signals. Nothing can have infinite power. However, mathematically it is more convenient to deal with power signals. We will use power signals to approximate the behavior of energy signals over the time intervals of interest.



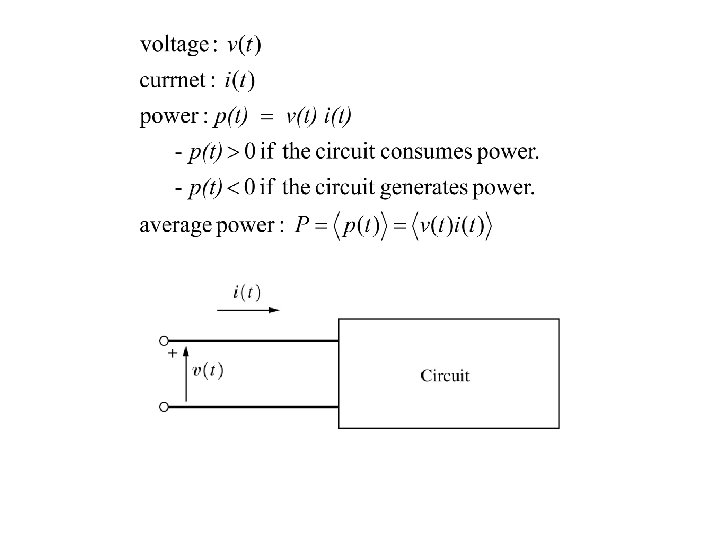
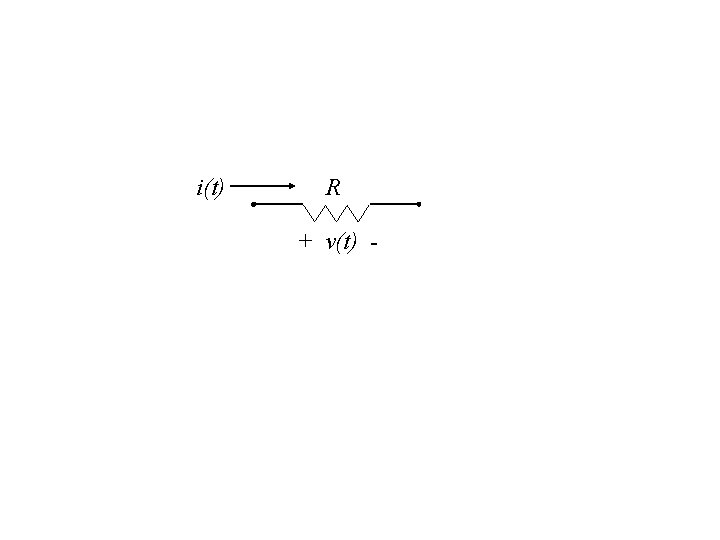
i(t) R + v(t) -

power in System signal, s(t) noise, n(t) power out System

The phasor is a complex number that carries the amplitude and phase angle information of a sinusoidal function. It does not include the angular frequency. Euler’s identify : Given


Fourier Transform Signal is a measurable, physical quantity which carries information. In time, it is quantified as w(t). Sometimes it is convenient to view through its frequency components. Fourier Transform (FT) is a mathematical tool to identify the presence of frequency component for any wave form.


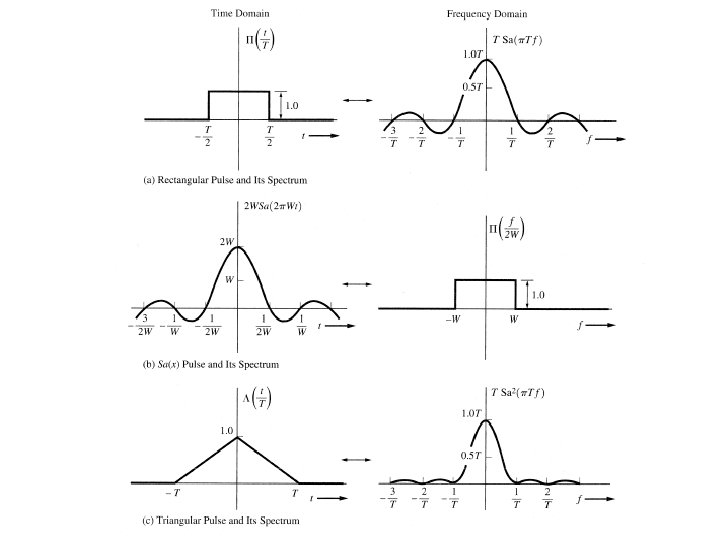
Note: It is in general difficult to evaluate the FT integrations for arbitrary functions. There are certain well known functions used in the FT along with the properties of the FT.

Properties of Fourier Transform If w(t) is real, W(-f) = W*(f). 1. 2. Linearity: a 1 w 1(t)+a 2 w 2(t) a 1 W 1(f) + a 2 W 2(f) 3. Time delay: w(t – T) = W(f) e-j 2 f. T 4. Frequency Translation: w(t) ej 2 fot W(f – fo) 5. Convolution: w 1(t)X w 2(t) W 1(f)W 2(f) 6. Multiplication: w 1(t)w 2(t) W 1(f)X W 2(f) Note: * is complex conjugate. X is convolution integral.


Parseval’s Theorem

Dirac Delta Function

Unit Step Function

More Commonly Used Functions



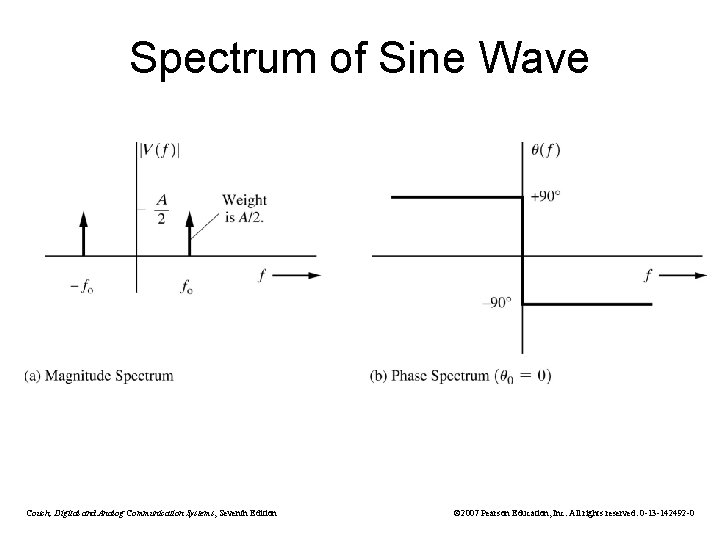
Spectrum of Sine Wave Couch, Digital and Analog Communication Systems, Seventh Edition © 2007 Pearson Education, Inc. All rights reserved. 0 -13 -142492 -0

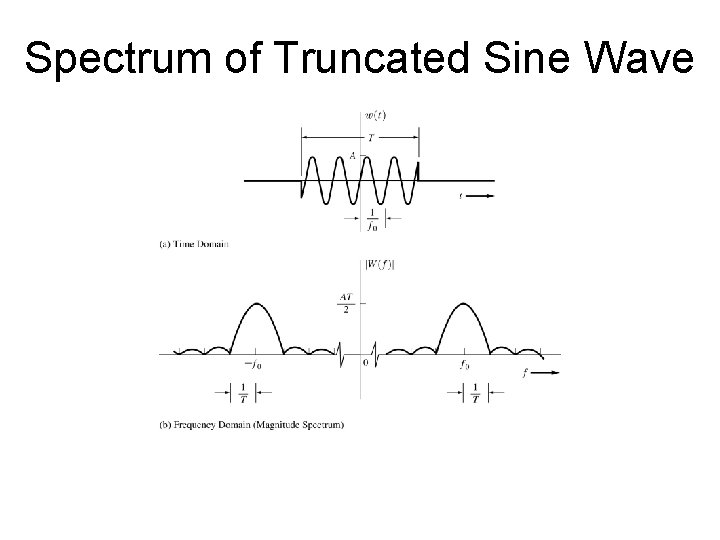
Figure 2– 8 Waveform and spectrum of a switched sinusoid. Spectrum of Truncated Sine Wave

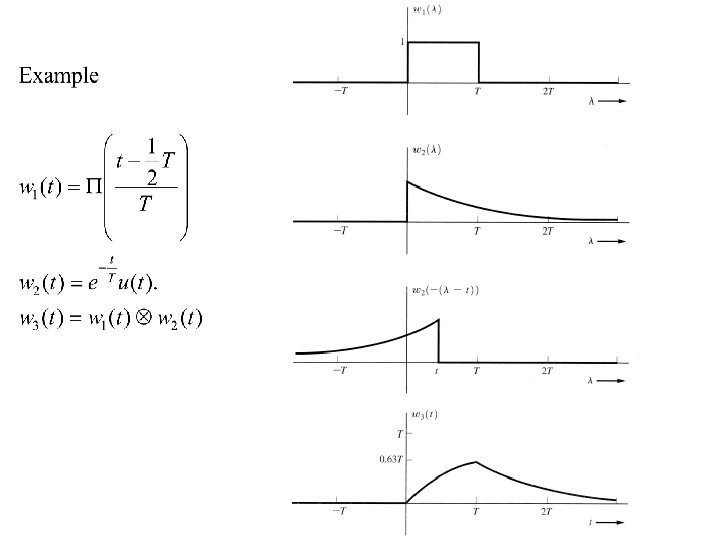
Example: Double Exponential

Convolution Supposed t is fixed at an arbitrary value. Within the integration, w 2(t- ) is a “horizontally flipped about =0, and move to the right by t version” of w 2( ). Now, multiply w 1( ) with w 2(t- ) for each point of . Then, integrate over - < < . The result is w 3(t) for this fixed value of t. Repeat this process for all values of t, - < t < .


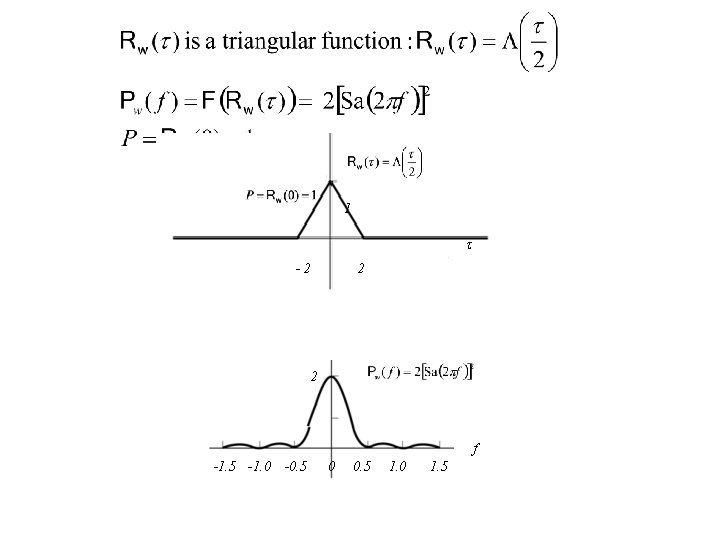
Power Spectrum Density

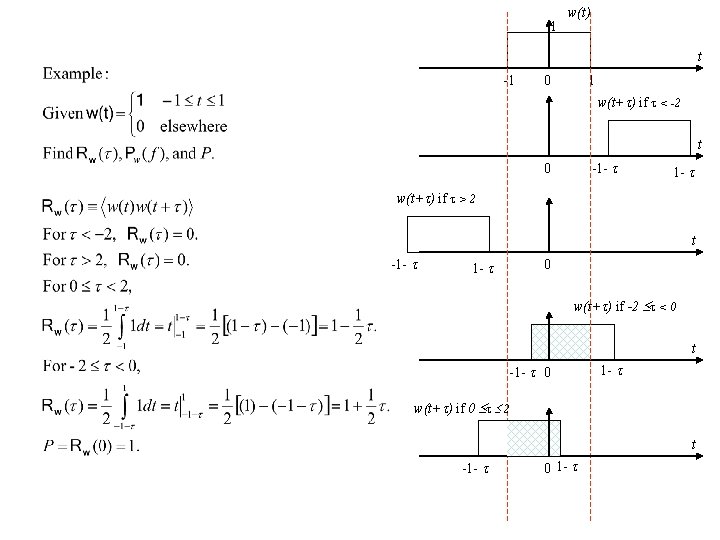
1 w(t) t -1 0 1 w(t+ ) if < -2 t -1 - 0 1 - w(t+ ) if > 2 t -1 - 0 1 - w(t+ ) if -2 < 0 t -1 - 0 1 - w(t+ ) if 0 2 t -1 - 0 1 -

1 -2 2 2 f -1. 5 -1. 0 -0. 5 0 0. 5 1. 0 1. 5

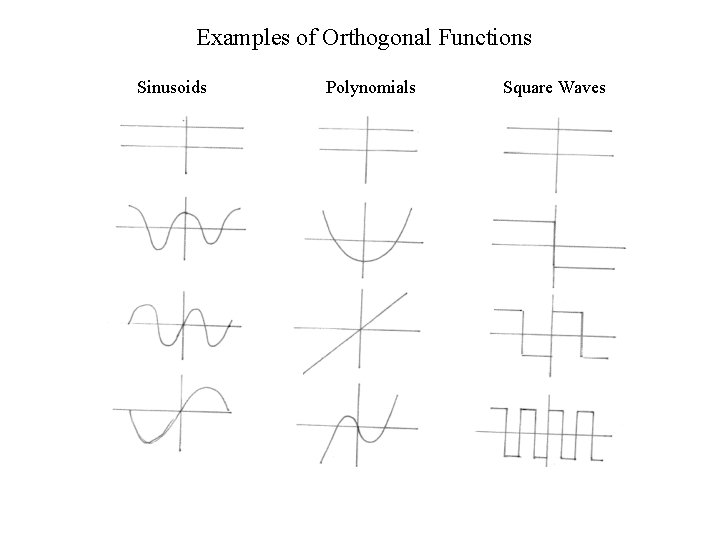
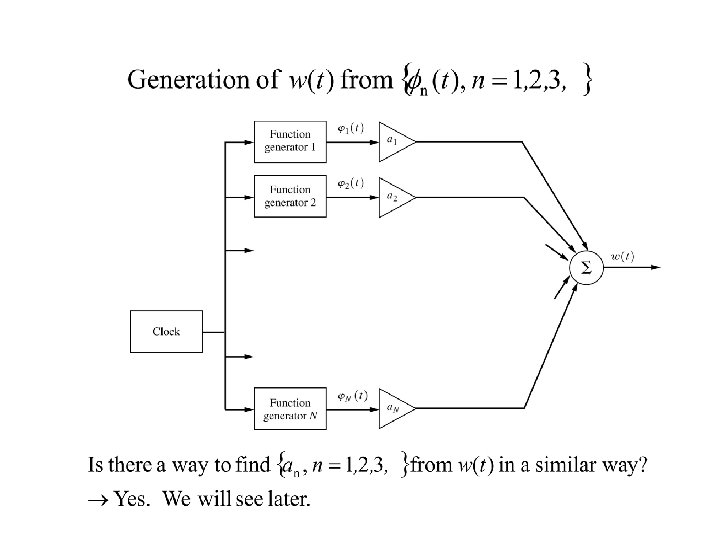
Orthogonal Series Representation


Examples of Orthogonal Functions Sinusoids Polynomials Square Waves




Fourier Series (pages 71 – 78 not covered)

Properties of Fourier Series


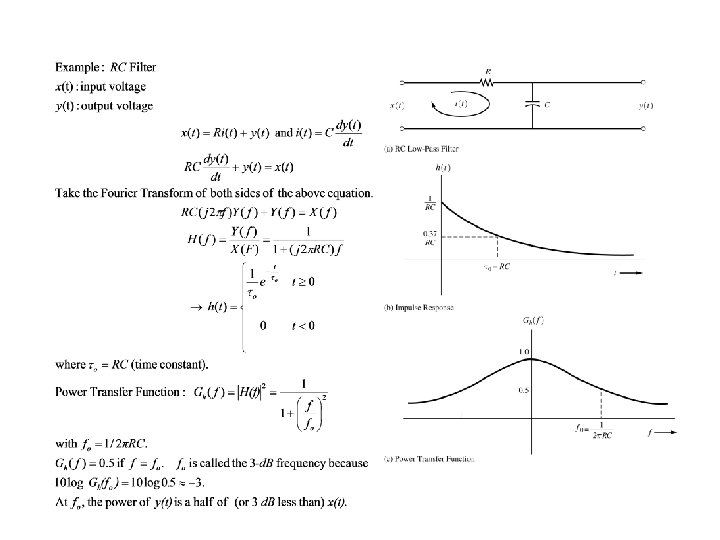
Impulse Response


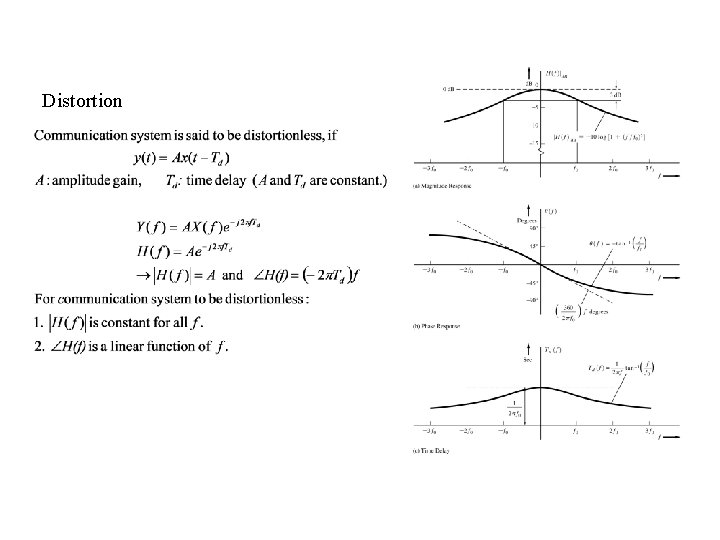
Distortion

Note: Sections 2. 7 and 2. 9 will be covered briefly. Section 2. 8 will not be covered.

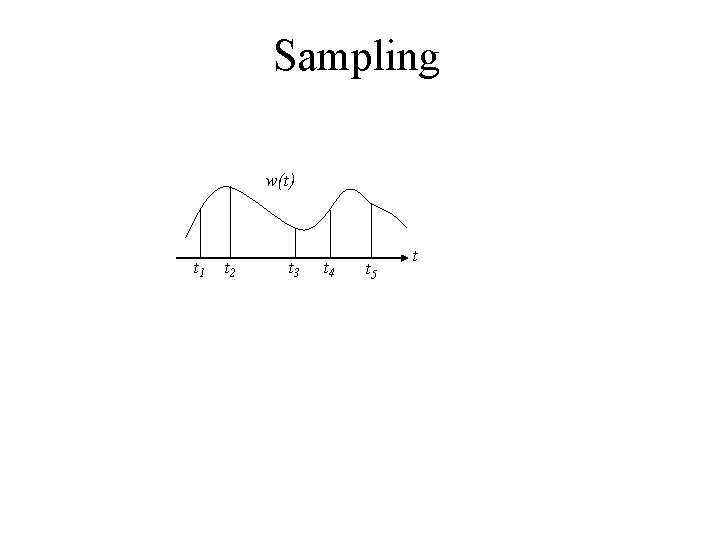
Sampling w(t) t 1 t 2 t 3 t 4 t 5 t


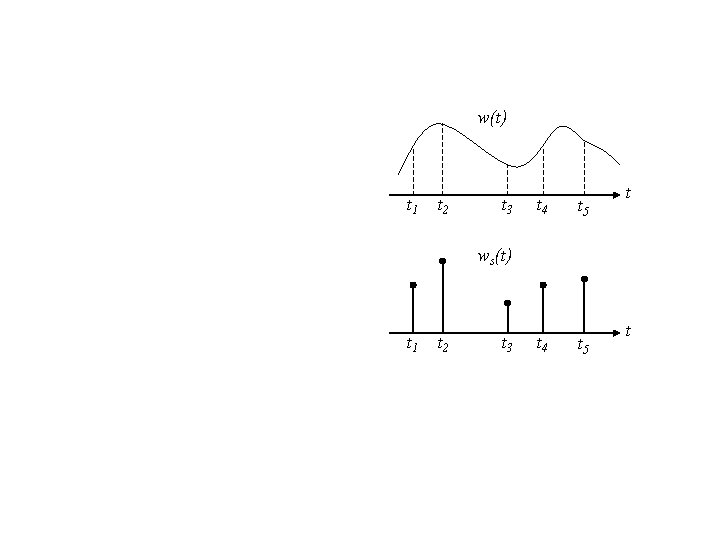
w(t) t 1 t 2 t 3 t 4 t 5 t ws(t) t 1 t 2 t 3 t 4 t 5 t

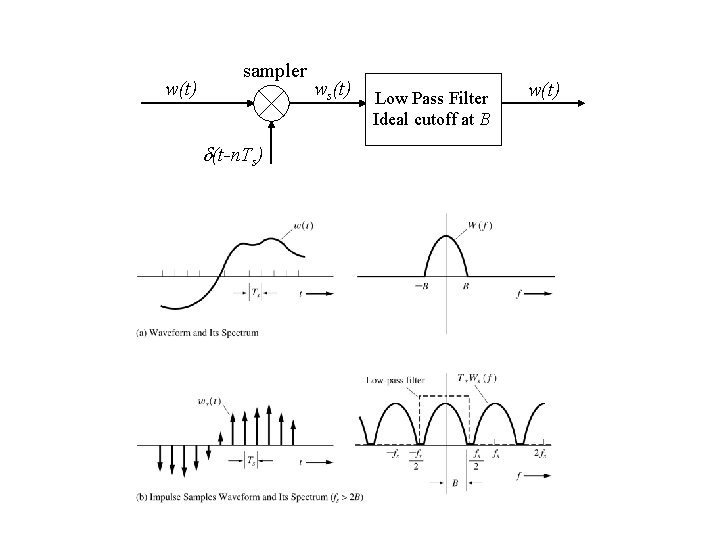
w(t) sampler (t-n. Ts) ws(t) Low Pass Filter Ideal cutoff at B w(t)

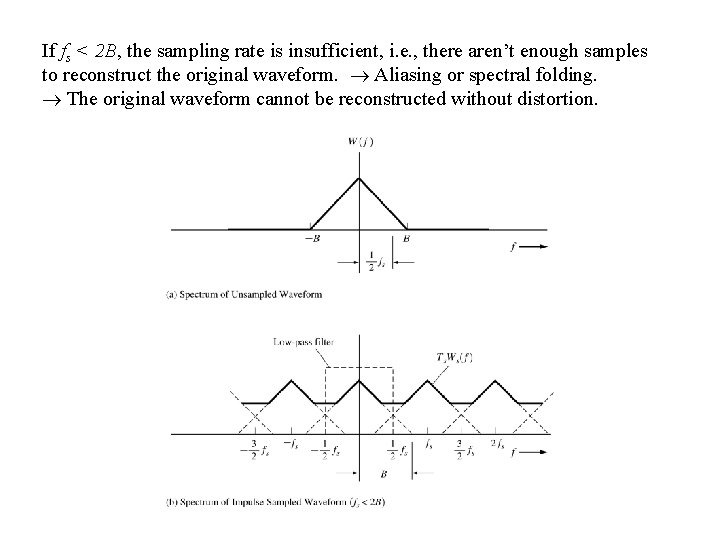
If fs < 2 B, the sampling rate is insufficient, i. e. , there aren’t enough samples to reconstruct the original waveform. Aliasing or spectral folding. The original waveform cannot be reconstructed without distortion.

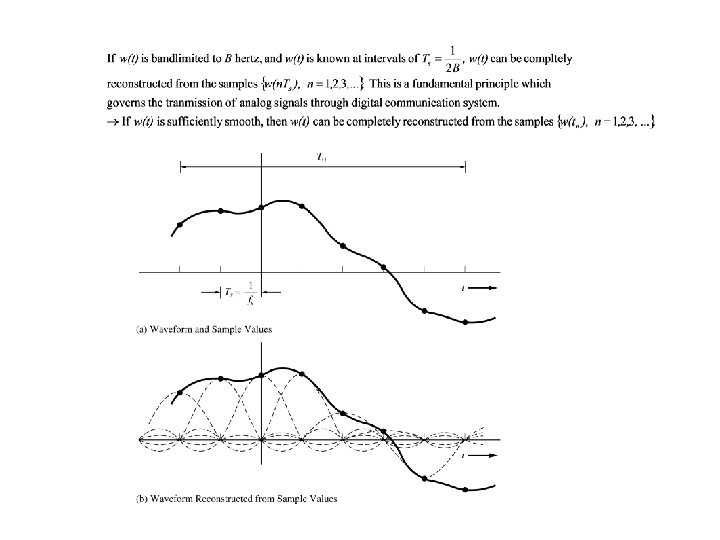
Dimensionality Theorem For a bandlimited waveform with bandwidth B hertz, if the waveform can be completely specified (i. e. , later reconstructed by an ideal low pass filter) by N=2 BTo samples during a time period of To, then N is the dimension of the wave form. Conversely, to estimate the bandwidth of a waveform, find a number N such that N=2 BTo is the minimum number of samples needed to reconstruct the waveform during a time period To. Then B follows. As To , any approximation goes to zero. A slightly modified version of this theorem is the Bandpass Dimensionality Theorem: Any bandpass waveform (with bandwidth B) can be determined by N=2 BTo samples taken during a period of To.

Data Rate Theorem (Corollary to Dimensionality Theorem) The maximum number of independent quantities which can be transmitted by a bandlimited channel (B hertz) during a time period of To is N=2 BTo. Definition. The baud rate of a digital communication system is the rate of symbols or quantities transmitted per second. From the Data Rate Theorem, the maximum baud rate of a system with a bandlimited channel (B hertz) is 2 B symbols / second. Definition. The data rate (or bit rate), R, of a system is the baud rate times the information content per symbol (H): R= 2 BH bits / second Suppose a source transmits one of M equally likely symbols. The information content of each symbol: H = log 2 (1/probablity of each symbol) = log 2 M R= 2 Blog 2 M Data rate is (also known as the Channel Capacity) is determined by (1) channel bandwidth and (2) channel SNR.

 Animals and human language chapter 2
Animals and human language chapter 2 Arbitrariness in human language and animal language
Arbitrariness in human language and animal language Communicative and informative signals
Communicative and informative signals Atomic emission spectra and the quantum mechanical model
Atomic emission spectra and the quantum mechanical model Atomic emmision spectrum
Atomic emmision spectrum Matter and materials grade 12
Matter and materials grade 12 The skin performs all of the following except
The skin performs all of the following except All of the following accurately describe hadoop
All of the following accurately describe hadoop If the creditors financial claim to property totals $1 000
If the creditors financial claim to property totals $1 000 Milady chapter 25 manicuring test answers
Milady chapter 25 manicuring test answers The two outer jovians appear bluish in color because
The two outer jovians appear bluish in color because Venus’s surface shows all of the following except
Venus’s surface shows all of the following except Diction refers to
Diction refers to This organelle contains pigments of all colors except green
This organelle contains pigments of all colors except green The man makes all the following mistakes except
The man makes all the following mistakes except Unlike other characters in the play creon displays
Unlike other characters in the play creon displays A punnett square shows all of the following except
A punnett square shows all of the following except External respiration vs internal respiration
External respiration vs internal respiration Strict constructionists favored congress exercising
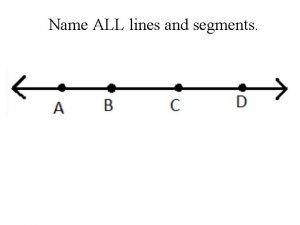
Strict constructionists favored congress exercising Name 3 points
Name 3 points Volleyball signals
Volleyball signals Vibrational spectra of metal carbonyls
Vibrational spectra of metal carbonyls Spectra tips
Spectra tips Spectra shropshire
Spectra shropshire Ethyl acetate ir spectrum
Ethyl acetate ir spectrum Fraunhoffer diffraction
Fraunhoffer diffraction Nitro group on ir
Nitro group on ir Spectroscopy equations
Spectroscopy equations Azza spectra
Azza spectra Alkanes ir spectrum
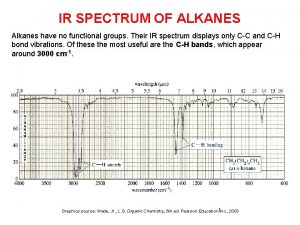
Alkanes ir spectrum Atomic emission spectra periodic table
Atomic emission spectra periodic table Periodic table of spectra
Periodic table of spectra Electronic spectra of coordination compounds
Electronic spectra of coordination compounds Electronic spectra of coordination compounds
Electronic spectra of coordination compounds Line spectra
Line spectra Why are atomic emission spectra discontinuous
Why are atomic emission spectra discontinuous Racah parameter
Racah parameter Electronic spectra of polyatomic molecules
Electronic spectra of polyatomic molecules Ir value chart
Ir value chart Vibronic spectra
Vibronic spectra Outline spectra
Outline spectra Supernova spectra
Supernova spectra What is the mulliken symbols for f spectroscopic term in
What is the mulliken symbols for f spectroscopic term in Uv spectra of dienes
Uv spectra of dienes Heisenberg uncertainty principle
Heisenberg uncertainty principle Uv spectra of dienes
Uv spectra of dienes Star spectra
Star spectra Correlation diagram in coordination chemistry
Correlation diagram in coordination chemistry Electromagnetci spectrum
Electromagnetci spectrum Spectra of diatomic molecules
Spectra of diatomic molecules