Chapter 10 Network Optimization Models 2015 Mc GrawHill

Chapter 10 Network Optimization Models © 2015 Mc. Graw-Hill Education. All rights reserved.

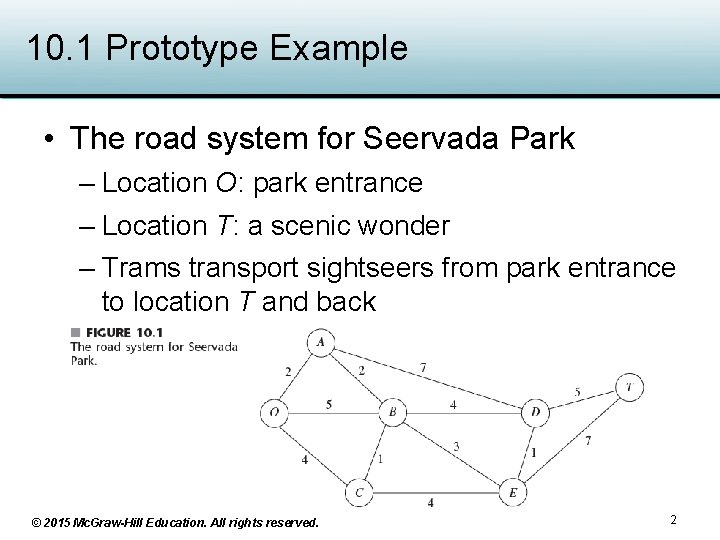
10. 1 Prototype Example • The road system for Seervada Park – Location O: park entrance – Location T: a scenic wonder – Trams transport sightseers from park entrance to location T and back © 2015 Mc. Graw-Hill Education. All rights reserved. 2

Prototype Example • Park management faces three problems – Determine the route with the smallest total distance • A shortest-path problem – Determine where telephone lines should be laid • A minimum spanning tree problem – Determine how to route tram to maximize number of trips during peak season • A maximum flow problem © 2015 Mc. Graw-Hill Education. All rights reserved. 3

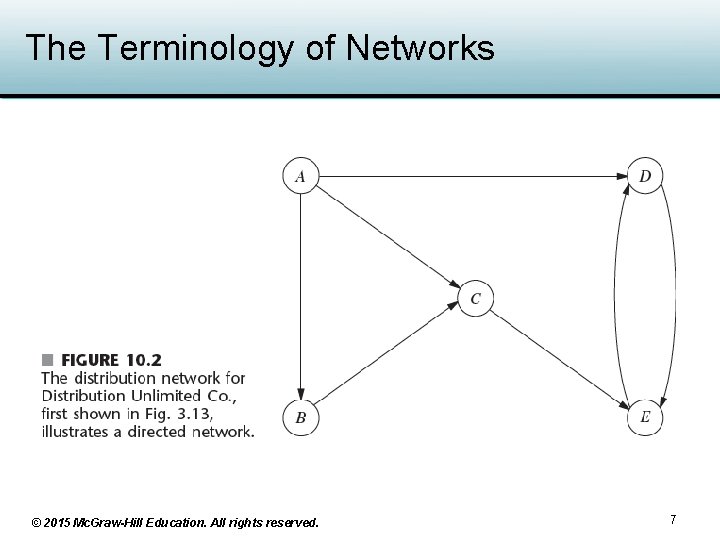
10. 2 The Terminology of Networks • Network consists of a set of points and a set of lines connecting points • Node: point (vertex) in the network • Lines: links, arcs, edges, or branches – Labeled by naming the node at each end • From node precedes the to node – Have a flow of some type through them • Directed arcs have unidirectional flow • Undirected arcs (links) allow bidirectional flow © 2015 Mc. Graw-Hill Education. All rights reserved. 4

The Terminology of Networks • Directed network – Network has only directed arcs • Undirected network – Network has only undirected arcs • Path between two nodes – A sequence of distinct arcs connecting the nodes • Directed path from node i to node j – Sequence of connecting arcs toward node j © 2015 Mc. Graw-Hill Education. All rights reserved. 5

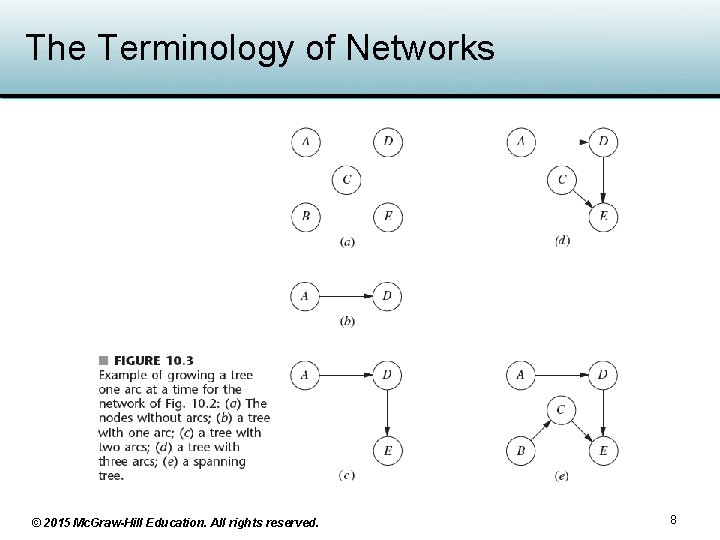
The Terminology of Networks • Undirected path from node i to node j – Sequence of connecting arcs whose direction can be with toward or away from node j • Connected network – Every pair of nodes in the network has at least one undirected path between them • Tree (spanning tree) – Connected network with no undirected cycles © 2015 Mc. Graw-Hill Education. All rights reserved. 6

The Terminology of Networks © 2015 Mc. Graw-Hill Education. All rights reserved. 7

The Terminology of Networks © 2015 Mc. Graw-Hill Education. All rights reserved. 8

The Terminology of Networks • Arc capacity – Maximum amount of flow that can be carried on a directed arc • Supply node – Flow out exceeds flow in • Demand node – Flow in exceeds flow out • Transshipment node – Flow in equals flow out © 2015 Mc. Graw-Hill Education. All rights reserved. 9

10. 3 The Shortest-Path Problem • Consider an undirected, connected network – Contains origin and destination nodes – Each link has a nonnegative distance • The problem – Find the shortest path from origin to destination © 2015 Mc. Graw-Hill Education. All rights reserved. 10

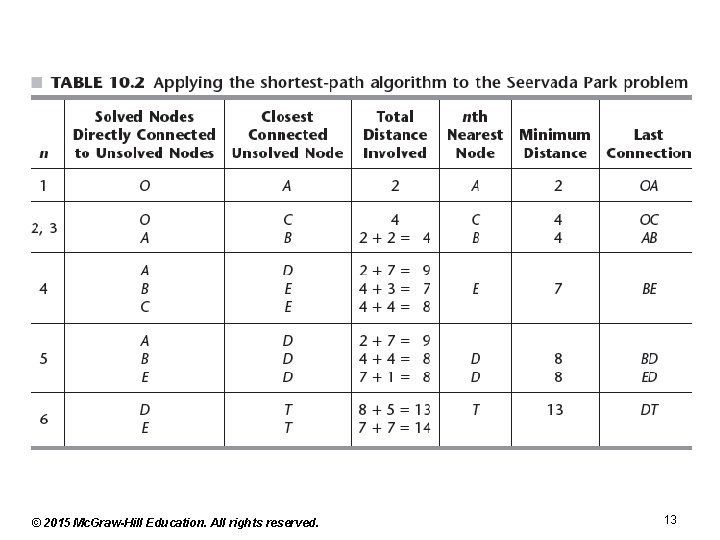
The Shortest-Path Problem • Algorithm – Objective of nth iteration: find the nth nearest node to the origin • Repeat for n = 1, 2… until destination is reached – Input for nth iteration: n − 1 nearest nodes to the origin, including shortest path and distance from the origin • These are called the solved nodes © 2015 Mc. Graw-Hill Education. All rights reserved. 11

The Shortest-Path Problem • Algorithm (cont’d. ) – Candidates for nth nearest node: unsolved node with shortest connecting link to the solved node – Calculation of nth nearest node • For each solved node and its candidate, add the distance between them and the distance of the shortest path from the origin to this solved node • Candidate with smallest total distance is the nth nearest node © 2015 Mc. Graw-Hill Education. All rights reserved. 12

© 2015 Mc. Graw-Hill Education. All rights reserved. 13

The Shortest-Path Problem • Shortest path for the Seervada park problem – Looking at last column in Table 10. 2, two potential shortest paths exist from the destination to the origin • T→ D → E → B → A → O or T→D→B→A→O • Total of 13 miles on either path © 2015 Mc. Graw-Hill Education. All rights reserved. 14

The Shortest-Path Problem • Network simplex method – An alternate option for solving shortest-path problems • Three categories of applications – Minimize total distance traveled – Minimize total cost of a sequence of activities – Minimize total time of a sequence of activities © 2015 Mc. Graw-Hill Education. All rights reserved. 15

10. 4 The Minimum Spanning Tree Problem • Given: nodes of a network, potential links, and positive length of each link if it is inserted into the network – Design the network by inserting links – A path must exist between every pair of nodes • Problem: minimize total length of links inserted into the network • Network of n nodes requires only n− 1 links – Choose the links to form a spanning tree © 2015 Mc. Graw-Hill Education. All rights reserved. 16

The Minimum Spanning Tree Problem • Applications – Design of telecommunications networks – Design of a lightly-used transportation network to minimize cost of providing links – Design network of power transmission lines – Electrical equipment wiring – Piping systems © 2015 Mc. Graw-Hill Education. All rights reserved. 17

The Minimum Spanning Tree Problem • Algorithm – Select any node arbitrarily and then add a link to connect it to its nearest node – Identify the unconnected node that is closest to a connected node, and add a link between them • Repeat until all nodes have been connected – Ties may be broken arbitrarily • There may be multiple optimal solutions © 2015 Mc. Graw-Hill Education. All rights reserved. 18

The Minimum Spanning Tree Problem • Example of graphical approach to implementing the algorithm – Problem: installing telephone lines in Seervada park – See Pages 384 -386 in the text for solution © 2015 Mc. Graw-Hill Education. All rights reserved. 19

10. 5 The Maximum Flow Problem • General problem description – All flow through a directed, connected network originates at a source, and terminates at a sink • Remaining nodes are transshipment nodes – Flow through an arc is allowed in only one direction (indicated by the arrowhead) • Maximum flow is given by arc capacity – Objective: maximize total flow from source to sink © 2015 Mc. Graw-Hill Education. All rights reserved. 20

The Maximum Flow Problem • Applications – Maximize flow through company’s distribution network from factories to customers – Maximize flow through company’s supply network from vendors to factories – Maximize oil flow through a system of pipelines – Maximize water flow through aqueducts – Maximize flow of vehicles through a transportation network © 2015 Mc. Graw-Hill Education. All rights reserved. 21

The Maximum Flow Problem • Algorithms – Simplex method can be used – Augmenting path algorithm is more efficient • Residual network – Remaining arc capacities after some flows have been assigned • Augmenting path – Directed path from source to sink in residual network such that every arc on path has positive residual capacity © 2015 Mc. Graw-Hill Education. All rights reserved. 22

The Maximum Flow Problem • Algorithm (each iteration follows these steps) – Identify an augmenting path • If none exists, net flows already constitute an optimal flow pattern – Identify the residual capacity, c* of this augmenting path • It will equal the minimum residual capacity of the arcs on this path – Increase the flow in this path by c* © 2015 Mc. Graw-Hill Education. All rights reserved. 23

The Maximum Flow Problem • Algorithm (cont’d. ) – Decrease by c* the residual capacity of each arc on this augmenting path – Increase by c* the residual capacity of each arc in the opposite direction on this augmenting path – Return to the first step • Example: Seervada park transportation problem – See Pages 390 -392 in the text © 2015 Mc. Graw-Hill Education. All rights reserved. 24

10. 6 The Minimum Cost Flow Problem • General description of the minimum cost flow problem – The network is directed and connected – At least one of the nodes is a supply node, and one of the other nodes is a demand node • All remaining nodes are transshipment nodes – Flow is only allowed in direction of the arrowhead • Arc capacity gives maximum allowable flow © 2015 Mc. Graw-Hill Education. All rights reserved. 25

The Minimum Cost Flow Problem • General description (cont’d. ) – Network has enough arcs with sufficient capacity to enable all flow generated at supply nodes to reach all demand nodes – Cost of flow through each arc is proportional to the amount of flow – Objective: minimize total cost of sending available supply through the network to meet the given demand © 2015 Mc. Graw-Hill Education. All rights reserved. 26

The Minimum Cost Flow Problem © 2015 Mc. Graw-Hill Education. All rights reserved. 27

The Minimum Cost Flow Problem • Linear programming problem formulation © 2015 Mc. Graw-Hill Education. All rights reserved. 28

The Minimum Cost Flow Problem • Feasible solutions property • Integer solutions property – For minimum cost flow problems where every bi and uij have integer values, all the basic variables in every basic feasible solution also have integer values © 2015 Mc. Graw-Hill Education. All rights reserved. 29

The Minimum Cost Flow Problem • Special cases that fit the minimum cost flow problem – The transportation problem – The assignment problem – The transshipment problem – The shortest-path problem – The maximum flow problem © 2015 Mc. Graw-Hill Education. All rights reserved. 30

The Minimum Cost Flow Problem • Network simplex method – An alternative method to solving the special cases when the special-purpose algorithms are not available © 2015 Mc. Graw-Hill Education. All rights reserved. 31

10. 7 The Network Simplex Method • Streamlined version of the simplex method – Same basic steps • Finding the entering basic variable • Determining the leaving basic variable • Solving for the new BF solution • General concepts of the method are covered in the text © 2015 Mc. Graw-Hill Education. All rights reserved. 32

The Network Simplex Method • Incorporate the upper bound technique: – To deal with the arc capacity constraints • Network representation of BF solutions – Basic arcs: arcs corresponding to basic variables • Key property: they never form undirected cycles – Nonbasic arcs: arcs corresponding to nonbasic variables © 2015 Mc. Graw-Hill Education. All rights reserved. 33

The Network Simplex Method • BF solutions can be obtained by solving spanning trees – For arcs not in the spanning tree, set the corresponding variables (xij or yij) equal to zero – For arcs in the spanning tree, solve for the corresponding variables (xij or yij) in the system of linear equations provided by the node constraints © 2015 Mc. Graw-Hill Education. All rights reserved. 34

The Network Simplex Method • Feasible spanning tree – Spanning tree whose solution from the node constraints also satisfies all the other constraints • Fundamental theorem for the network simplex method – Basic solutions are spanning tree solutions (and conversely) – BF solutions are solutions for feasible spanning trees (and conversely) © 2015 Mc. Graw-Hill Education. All rights reserved. 35

10. 8 A Network Model for Optimizing a Project’s Time-Cost Trade-off • Network based OR techniques developed in the 1950 s – PERT (Program Evaluation Review Technique) – CPM (Critical Path Method) – Both are used in project management • Concepts have merged into PERT/CPM • CPM method for time-cost tradeoff – Addresses a project with a specific deadline © 2015 Mc. Graw-Hill Education. All rights reserved. 36

A Network Model for Optimizing a Project’s Time-Cost Trade-off • CPM method for time-cost trade-off (cont’d. ) – Problem: find optimal plan for expediting activities to minimize the total cost of completing the project within the deadline • General approach – Use a network to display the various activities • And the order in which they need to be performed – Form optimization model • Solve using linear programming © 2015 Mc. Graw-Hill Education. All rights reserved. 37

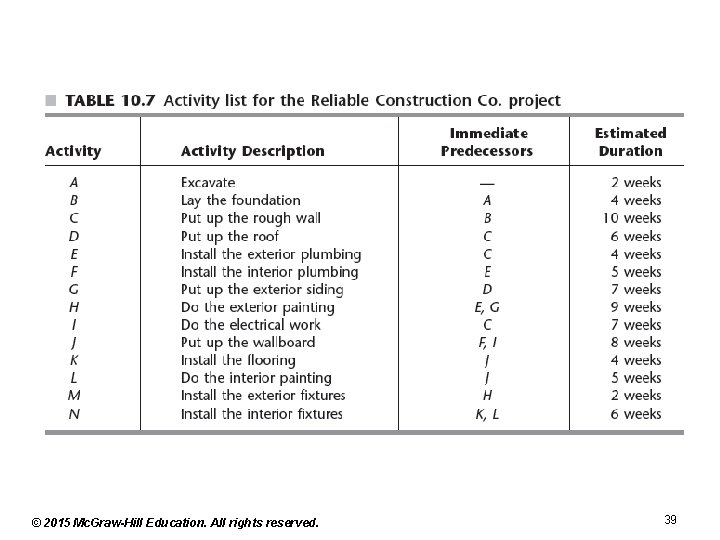
A Network Model for Optimizing a Project’s Time-Cost Trade-off • Prototype example – The Reliable Construction Co. won the contract to construct a new plant within a time period of 40 weeks – See Table 10. 7 • Project network options – Activity-on-arc (AOA) • Each activity is represented by an arc • Nodes separate activities from predecessors • Used by original versions of PERT and CPM © 2015 Mc. Graw-Hill Education. All rights reserved. 38

© 2015 Mc. Graw-Hill Education. All rights reserved. 39

A Network Model for Optimizing a Project’s Time-Cost Trade-off • Project network options (cont’d. ) – Activity-on-node (AON) • Each activity is represented by a node • Arcs show precedence relationships between activities • Has several advantages over AOA • May become the standard format for project networks © 2015 Mc. Graw-Hill Education. All rights reserved. 40

A Network Model for Optimizing a Project’s Time-Cost Trade-off • Path – One of the routes following the arcs from start to finish • The critical path – Relevant: length of each path through the network – Sum of estimated durations of activities on the path © 2015 Mc. Graw-Hill Education. All rights reserved. 41

A Network Model for Optimizing a Project’s Time-Cost Trade-off • Estimating the critical path (project duration) for the Reliable Construction Co. example – See Pages 415 -417 in the text • Crashing an activity – Taking special costly measures to reduce an activity’s duration – Crashing the project involves crashing a number of activities © 2015 Mc. Graw-Hill Education. All rights reserved. 42

A Network Model for Optimizing a Project’s Time-Cost Trade-off • Example problem: determine least expensive way to crash activities to reduce overall duration to 40 weeks • Solution methods – Marginal cost analysis • See Table 10. 10 and Table 10. 11 on Pages 419 and 420 of the text – Linear programming • Follow steps on Pages 420 -424 of the text © 2015 Mc. Graw-Hill Education. All rights reserved. 43

10. 9 Conclusions • Problems addressed with network models – Optimizing an existing network – Designing a new network • Minimum spanning tree problem • CPM method of time-cost trade-offs – Powerful way of applying network optimization to project management © 2015 Mc. Graw-Hill Education. All rights reserved. 44