Chapter 10 Estimating Means with Confidence Section 10














































- Slides: 49

Chapter 10 Estimating Means with Confidence Section 10. 1 Estimating a Population Mean

Estimating a Population Mean LEARNING TARGETS By the end of this section, you should be able to: üDETERMINE the critical value for calculating a C% confidence interval for a population mean using a table or technology. üSTATE and CHECK the Random, 10%, and Normal/Large Sample conditions for constructing a confidence interval for a population mean. üCONSTRUCT and INTERPRET a confidence interval for a population mean. Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ statistic ± (critical value)(standard deviation of the statistic) Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ statistic ± (critical value)(standard deviation of the statistic) Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ statistic ± (critical value)(standard deviation of the statistic) Unfortunately, if we don’t know the true value of µ, we rarely know the true value of σ either. Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ We can use sx as an estimate for σ, but things don’t work out as nicely as we might like. Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ We can use sx as an estimate for σ, but things don’t work out as nicely as we might like. Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ We can use sx as an estimate for σ, but things don’t work out as nicely as we might like. We used a 99% confidence level, but only 92. 5% of our 1000 intervals actually captured µ. Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ We can use sx as an estimate for σ, but things don’t work out as nicely as we might like. We used a 99% confidence level, but only 92. 5% of our 1000 intervals actually captured µ. To achieve a 99% capture rate, we need to multiply by a larger critical value. But what critical value should we use? Starnes/Tabor, The Practice of Statistics

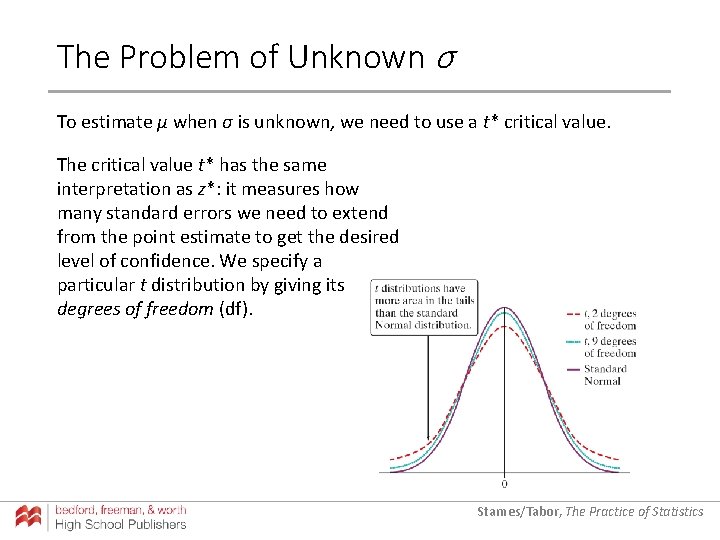
The Problem of Unknown σ To estimate µ when σ is unknown, we need to use a t* critical value. Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ To estimate µ when σ is unknown, we need to use a t* critical value. The critical value t* has the same interpretation as z*: it measures how many standard errors we need to extend from the point estimate to get the desired level of confidence. We specify a particular t distribution by giving its degrees of freedom (df). Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ Problem: What critical value t* from Table B should be used in constructing a confidence interval for the population mean in each of the following settings? Confirm your answers using technology. (a) A 95% confidence interval based on an SRS of size n = 12 (b) A 90% confidence interval from a random sample of 48 observations Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ Problem: What critical value t* from Table B should be used in constructing a confidence interval for the population mean in each of the following settings? Confirm your answers using technology. (a) A 95% confidence interval based on an SRS of size n = 12 (b) A 90% confidence interval from a random sample of 48 observations (a) t* = 2. 201 Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ Problem: What critical value t* from Table B should be used in constructing a confidence interval for the population mean in each of the following settings? Confirm your answers using technology. (a) A 95% confidence interval based on an SRS of size n = 12 (b) A 90% confidence interval from a random sample of 48 observations (b) t* = 1. 684 Starnes/Tabor, The Practice of Statistics

The Problem of Unknown σ Problem: What critical value t* from Table B should be used in constructing a confidence interval for the population mean in each of the following settings? Confirm your answers using technology. (a) A 95% confidence interval based on an SRS of size n = 12 (b) A 90% confidence interval from a random sample of 48 observations (a) inv. T(0. 025, 11), so t* = 2. 201 (b) inv. T(0. 05, 47), so t* = 1. 684 Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ 1. The Random condition is crucial for doing inference. If the data don’t come from a random sample, you can’t draw conclusions about a larger population. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ 1. The Random condition is crucial for doing inference. If the data don’t come from a random sample, you can’t draw conclusions about a larger population. 2. When sampling without replacement, the 10% condition ensures that our formula for the standard deviation is approximately correct. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ 1. The Random condition is crucial for doing inference. If the data don’t come from a random sample, you can’t draw conclusions about a larger population. 2. When sampling without replacement, the 10% condition ensures that our formula for the standard deviation is approximately correct. 3. The Normal/Large Sample condition to ensure it is appropriate to use a t distribution to calculate the t* critical value. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ Conditions for Constructing a Confidence Interval about a Mean • Random: The data come from a random sample from the population of interest. o 10%: When sampling without replacement, n < 0. 10 N. • Normal/Large sample: The population has a Normal distribution OR The sample size is large (n ≥ 30) OR If the population distribution has unknown shape and n < 30, use a graph of the sample data to assess the Normality of the population. Do not use t procedures if the graph shows strong skewness or outliers. Starnes/Tabor, The Practice of Statistics

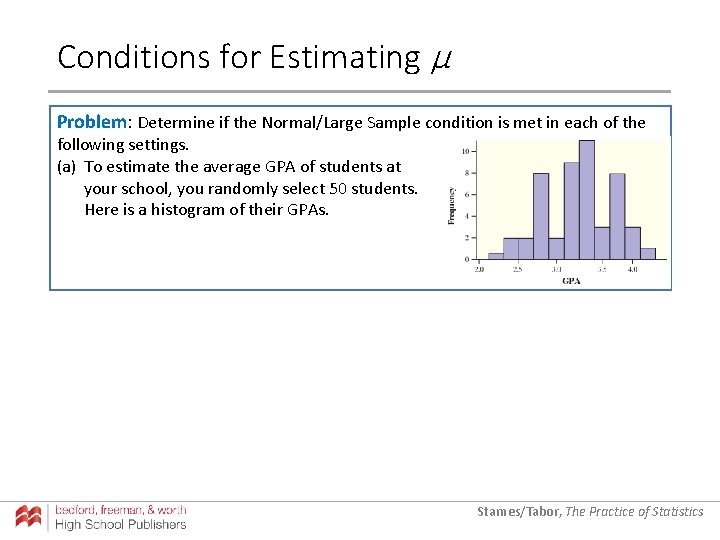
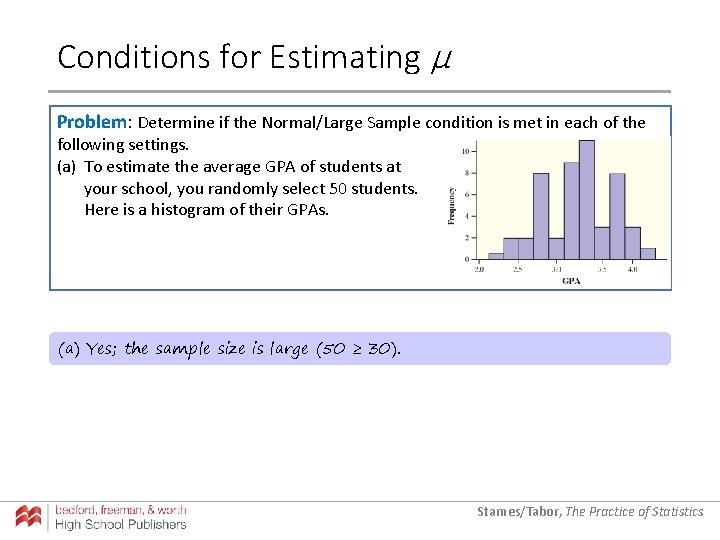
Conditions for Estimating µ Problem: Determine if the Normal/Large Sample condition is met in each of the following settings. (a) To estimate the average GPA of students at your school, you randomly select 50 students. Here is a histogram of their GPAs. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ Problem: Determine if the Normal/Large Sample condition is met in each of the following settings. (a) To estimate the average GPA of students at your school, you randomly select 50 students. Here is a histogram of their GPAs. (a) Yes; the sample size is large (50 ≥ 30). Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ Problem: Determine if the Normal/Large Sample condition is met in each of the following settings. (b) How much force does it take to pull wood apart? The stemplot shows the force (in pounds) required to pull a piece of Douglas fir apart for each of 20 randomly selected pieces. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ Problem: Determine if the Normal/Large Sample condition is met in each of the following settings. (b) How much force does it take to pull wood apart? The stemplot shows the force (in pounds) required to pull a piece of Douglas fir apart for each of 20 randomly selected pieces. (b) No; the stemplot is strongly skewed to the left with possible low outliers and n = 20 < 30. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ Problem: Determine if the Normal/Large Sample condition is met in each of the following settings. (c) Suppose you want to estimate the mean SAT Math score at a large high school. Here is a boxplot of the SAT Math scores for a random sample of 20 students at the school. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ Problem: Determine if the Normal/Large Sample condition is met in each of the following settings. (c) Suppose you want to estimate the mean SAT Math score at a large high school. Here is a boxplot of the SAT Math scores for a random sample of 20 students at the school. (c) Yes; even though n = 20 < 30, the boxplot is only moderately skewed to the right and there are no outliers. Starnes/Tabor, The Practice of Statistics

Conditions for Estimating µ AP® Exam Tip If a question on the AP® Statistics exam asks you to construct and interpret a confidence interval, all the conditions should be met. However, you are still required to state the conditions and show evidence that they are met—including a graph if the sample size is small and the data are provided. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Confidence Intervals: A Four-Step Process State: State the parameter you want to estimate and the confidence level. Plan: Identify the appropriate inference method and check conditions. Do: If the conditions are met, perform calculations. Conclude: Interpret your interval in the context of the problem. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ The One-Sample t Interval for a Population Mean Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Niloo/Shutterstock. com Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: (a) Construct and interpret a 95% confidence interval for the mean number of books read by all Americans in the previous 12 months. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: (a) Construct and interpret a 95% confidence interval for the mean number of books read by all Americans in the previous 12 months. STATE: 95% CI for µ = the true mean number of books read by all American adults in the previous 12 months. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: (a) Construct and interpret a 95% confidence interval for the mean number of books read by all Americans in the previous 12 months. STATE: 95% CI for µ = the true mean number of books read by all American adults in the previous 12 months. PLAN: One-sample t interval for µ • Random: Random sample of 1520 American adults ✓ º 10%: 1520 is less than 10% of all American adults ✓ • Normal/Large Sample: The sample size is large (n = 1520 ≥ 30). ✓ Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: (a) Construct and interpret a 95% confidence interval for the mean number of books read by all Americans in the previous 12 months. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: (a) Construct and interpret a 95% confidence interval for the mean number of books read by all Americans in the previous 12 months. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: (b) In 2011, Pew reported that American adults read an average of 14 books in the previous 12 months. Does your interval from part (a) provide convincing evidence that the 2016 mean is different than 14 books? Explain your answer. Yes; because 14 is not in the confidence interval, 14 is not a plausible value for the mean number of books read by all American adults in the previous 12 months. Starnes/Tabor, The Practice of Statistics

Problem: A manufacturer of high-resolution video terminals must control the tension on the mesh of fine wires that lies behind the surface of the viewing screen. Too much tension will tear the mesh, and too little will allow wrinkles. The tension is measured by an electrical device with output readings in millivolts (m. V). Some variation is inherent in the production process. Here are the tension readings from a random sample of 20 screens from a single day’s production: Pgiam/Getty Images Constructing a Confidence Interval for µ Construct and interpret a 90% confidence interval for the mean tension µ of all the screens produced on this day. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: Construct and interpret a 90% confidence interval for the mean tension µ of all the screens produced on this day. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: Construct and interpret a 90% confidence interval for the mean tension µ of all the screens produced on this day. STATE: 90% CI for µ = the true mean tension of all the video terminals produced this day. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: Construct and interpret a 90% confidence interval for the mean tension µ of all the screens produced on this day. STATE: 90% CI for µ = the true mean tension of all the video terminals produced this day. PLAN: One-sample t interval for µ • Random: Random sample of 20 screens produced that day ✓ º 10%: Assume that 20 is less than 10% of all video terminals produced that day. ✓ • Normal/Large Sample: The dotplot does not show strong skewness or outliers. ✓ Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: Construct and interpret a 90% confidence interval for the mean tension µ of all the screens produced on this day. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ Problem: Construct and interpret a 90% confidence interval for the mean tension µ of all the screens produced on this day. Starnes/Tabor, The Practice of Statistics

Constructing a Confidence Interval for µ AP® Exam Tip It is not enough just to make a graph of the data on your calculator when assessing Normality. You must sketch the graph on your paper to receive credit. You don’t have to draw multiple graphs—any appropriate graph will do. Starnes/Tabor, The Practice of Statistics

More About the Margin of Error In Chapter 8, you learned how different factors affect the margin of error when calculating a confidence interval for a population proportion. The lessons are the same in this section: Starnes/Tabor, The Practice of Statistics

More About the Margin of Error In Chapter 8, you learned how different factors affect the margin of error when calculating a confidence interval for a population proportion. The lessons are the same in this section: • The margin of error decreases as the sample size increases, assuming the confidence level and sample standard deviation sx remain the same. Starnes/Tabor, The Practice of Statistics

More About the Margin of Error In Chapter 8, you learned how different factors affect the margin of error when calculating a confidence interval for a population proportion. The lessons are the same in this section: • The margin of error decreases as the sample size increases, assuming the confidence level and sample standard deviation sx remain the same. • The margin of error is proportional to 1/ n, so quadrupling the sample size will cut the margin of error in half, assuming everything else remains the same. Starnes/Tabor, The Practice of Statistics

More About the Margin of Error In Chapter 8, you learned how different factors affect the margin of error when calculating a confidence interval for a population proportion. The lessons are the same in this section: • The margin of error decreases as the sample size increases, assuming the confidence level and sample standard deviation sx remain the same. • The margin of error is proportional to 1/ n, so quadrupling the sample size will cut the margin of error in half, assuming everything else remains the same. • The margin of error will be larger for higher confidence levels. This makes sense, as wider intervals will have a greater capture rate than narrower intervals. Starnes/Tabor, The Practice of Statistics

More About the Margin of Error In Chapter 8, you learned how different factors affect the margin of error when calculating a confidence interval for a population proportion. The lessons are the same in this section: • The margin of error decreases as the sample size increases, assuming the confidence level and sample standard deviation sx remain the same. • The margin of error is proportional to 1/ n, so quadrupling the sample size will cut the margin of error in half, assuming everything else remains the same. • The margin of error will be larger for higher confidence levels. This makes sense, as wider intervals will have a greater capture rate than narrower intervals. • The margin of error doesn’t account for bias in the data collection process, only sampling variability. Starnes/Tabor, The Practice of Statistics

Section Summary LEARNING TARGETS After this section, you should be able to: üDETERMINE the critical value for calculating a C% confidence interval for a population mean using a table or technology. üSTATE and CHECK the Random, 10%, and Normal/Large Sample conditions for constructing a confidence interval for a population mean. üCONSTRUCT and INTERPRET a confidence interval for a population mean. Starnes/Tabor, The Practice of Statistics
 Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Chapter 8 estimating with confidence
Chapter 8 estimating with confidence Confidence interval vs confidence level
Confidence interval vs confidence level Confidence interval z value
Confidence interval z value Estimating the difference between two means
Estimating the difference between two means Mean difference formula
Mean difference formula Confidence interval difference of means
Confidence interval difference of means Chapter 3 section 3 constitutional change by other means
Chapter 3 section 3 constitutional change by other means Quadrilateral pentagon hexagon octagon
Quadrilateral pentagon hexagon octagon Morphe means in metamorphism
Morphe means in metamorphism Meta means change and morph means heat
Meta means change and morph means heat Bio means life diversity means
Bio means life diversity means Bio means life logy means
Bio means life logy means Section quick check chapter 10 section 1 meiosis answer key
Section quick check chapter 10 section 1 meiosis answer key Chapter 19 confidence intervals for proportions
Chapter 19 confidence intervals for proportions Chapter 18 confidence intervals for proportions
Chapter 18 confidence intervals for proportions Chapter 19 confidence intervals for proportions
Chapter 19 confidence intervals for proportions When is stage fright most evident
When is stage fright most evident Chapter 7 confidence intervals and sample size
Chapter 7 confidence intervals and sample size Voyage estimating decision support system
Voyage estimating decision support system Rounding and estimating
Rounding and estimating Mcaces mii
Mcaces mii Estimating the degradation function
Estimating the degradation function Gao cost estimating guide
Gao cost estimating guide Estimation with decimals
Estimation with decimals Tendering and estimating
Tendering and estimating Falguni aggarwal
Falguni aggarwal Estimating earthwork volumes
Estimating earthwork volumes Concrete weight per cubic foot
Concrete weight per cubic foot Estimating avogadro's number lab
Estimating avogadro's number lab Electrical conduit installation estimating
Electrical conduit installation estimating Cost analysis and estimating for engineering and management
Cost analysis and estimating for engineering and management What is the point estimate of μ?
What is the point estimate of μ? 12-1 estimating limits graphically
12-1 estimating limits graphically Agile estimating and planning
Agile estimating and planning Determining time of death worksheet
Determining time of death worksheet Estimating with percents
Estimating with percents Estimating limit values from tables
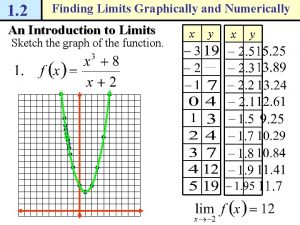
Estimating limit values from tables Finding limits graphically
Finding limits graphically Estimate whole numbers
Estimate whole numbers Hurdle principle
Hurdle principle Front end rounding decimals
Front end rounding decimals Bluebeam checkmark tool
Bluebeam checkmark tool Approximating square roots to the nearest hundredth
Approximating square roots to the nearest hundredth Estimating products of fractions
Estimating products of fractions Estimating sums and differences of fractions
Estimating sums and differences of fractions Estimating a population proportion
Estimating a population proportion Unit rate estimating
Unit rate estimating Estimating square roots word problems
Estimating square roots word problems