ESTIMATING with confidence Confidence INterval A confidence interval

ESTIMATING with confidence

Confidence INterval A confidence interval gives an estimated range of values which is likely to include an unknown population parameter, the estimated range being calculated from a given set of sample data.

CI: the Basic The admission directors at the Big City University has a novel idea. He proposes using the IQ scores of current students as a marketing tool. So the director gives the IQ test to an SRS of 50 of the university's 5000 freshmen. The mean IQ score of the sample is 112. What can the director say about the mean score of the population of all 5000 freshmen?

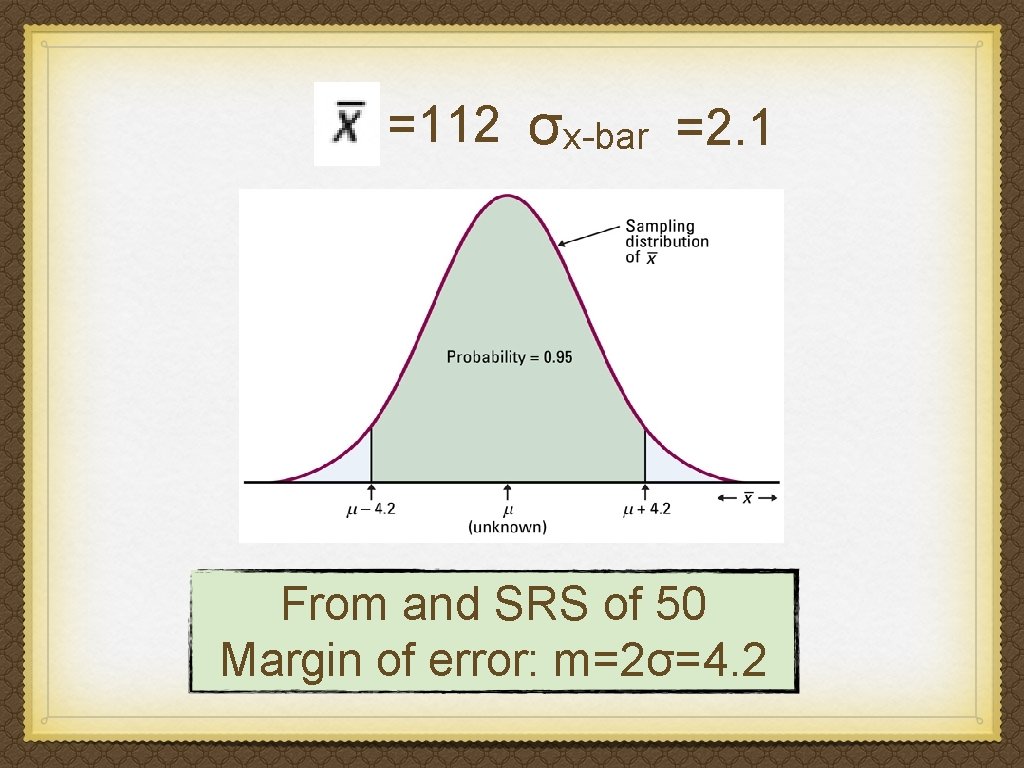
Supposed we know the standard deviation σ=15 =112 n=50 N=5 000 σx-bar = 15 / √ 50 =2. 1

=112 σx-bar =2. 1 From and SRS of 50 Margin of error: m=2σ=4. 2

Conclusion: IQ @ BCU _ Our sample of 50 - freshmen gave x = 112. The resulting interval is 112 ± 4. 2, (107. 8, 116. 2). We say that we are 95% confident that the unknown mean IQ score for all BCU freshmen is between 107. 8 and 116. 2 1. The interval between 107. 8 and 116. 2 contains the true µ. 2. Our SRS was one of the few samples for which x is not within 4. 2 points of the true µ. Only 5% of all samples give such inaccurate result

Let’s collect several sets of SRS of 50 students

EXAMPLE Bianca wanted to know the average weight of all the female students in UCLA. She went to UCLA and surveyed 50 female students in random and found out that their mean weight is 135 lbs. She estimated that the population standard deviation is about 3. 5 lbs. With all the information that she gathered, How can she estimate the true average weight of all the female students within 2 standard

Confidence INterval and Confidence Level A level C confidence interval for a parameter has 2 points: • A confidence interval calculated from the data, usually form Estimate ± margin of error • A confidence interval C which gives the probability that the interval will capture the true parameter value in repeated samples. That is, the confidence level is the success rate for the method

Conditions for Constructing the Confidence Interval for ℳ 1. The data come from SRS from the population of interest. 2. The sampling distribution of x is _ approximately Normal. 3. Individual observations are independent; when sampling without replacement, the population size N is at least 10 times the sample size of n.

AP Test TIP Common error for students taking AP Test: Failure to identify the conditions by which they are justified in constructing a confidence interval.

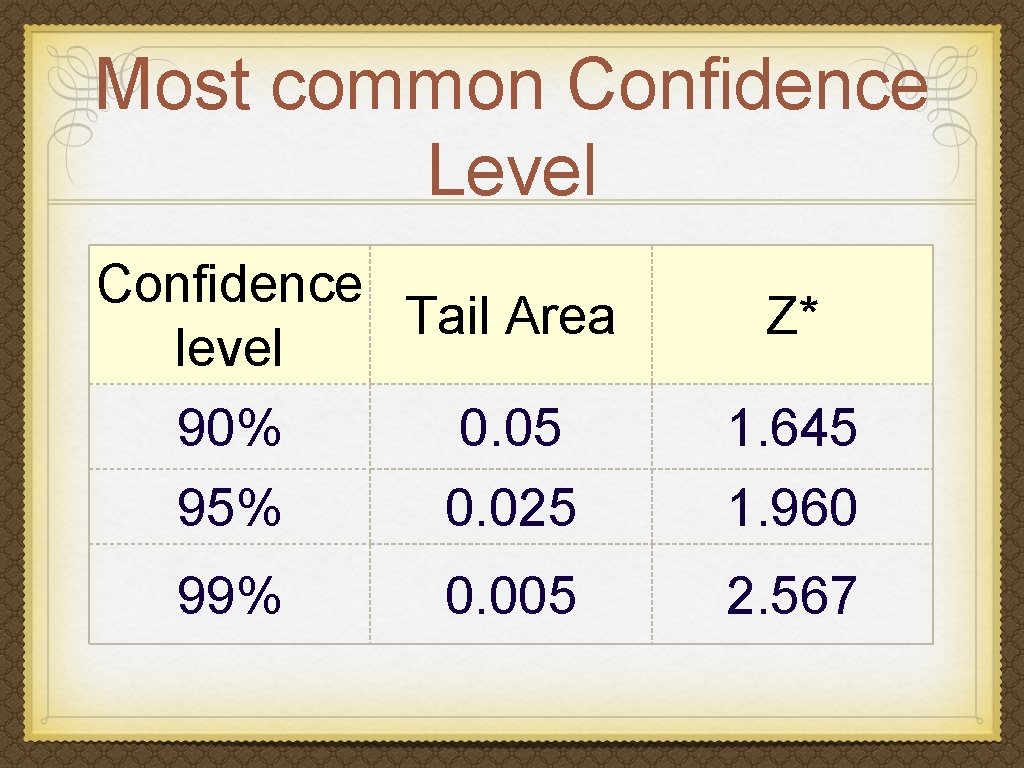
Most common Confidence Level Confidence Tail Area level Z* 90% 0. 05 1. 645 95% 0. 025 1. 960 99% 0. 005 2. 567

Confidence INterval for a populations σ MEAN ( is known) _ X ± z* σ √n

Inference toolbox Step 1: Identify the population of interest and the parameter you want to draw conclusion about. Step 2: Choose the appropriate inference procedure. Verify the conditions for using the selected procedure. CI: estimate ± margin of error Step 4: Interpret your result in the context of the problem

IQ TEST SCORES Here are the IQ test scores of 31 7 th grade girls in a midwestern school district: 114 100 104 89 102 91 114 103 105 108 130 120 132 111 128 119 86 72 111 103 74 112 107 103 98 96 112 93 - Supposed that the standard deviation of IQ scores in this population is know to be σ=15. Construct and interpret a 99% confidence interval for the mean IQ score in the population.

SRS: The data came from 7 th grade girls in a midwestern school distric Normality: Since the sample came from 31 7 th grade students, we can say that from the Central Limit Theorem that the sampling distribution of x-bar will be approximately Normal. Independence: from the 1 st rule of thumb in sample proportion, where N≧ 10, a sample size of 310 is more likely less than the population of all 7 th grade female midwestern students. The 99% CI for ℳ is: 105. 84 ± 2. 576 (15/√ 31) =105. 84 ± 6. 94 =(98. 90, 112. 78) With 99% confidence, we estimate the mean IQ score for all 7 th grade girls in the school district to be between 98. 90 and 112. 78 IQ points

Interpreting Confidence Interval

Interpreting Confidence Interval When collecting ______ samples repeatedly, we are ____ confident that the true µ will be contained in that interval.