Hypothesis Testing Objectives n Students should be able

Hypothesis Testing Objectives: n Students should be able to identify the null and alternative (research) hypotheses in a statistical test n Students should know the difference between one-and two-directional hypothesis testing n Students should know what alpha, beta, power, and p-values are n Students should be able to identify/define type I and type II errors n Students should understand the differences between statistical significance and clinical importance n Students should know how to determine statistical significance given alpha and a calculated p-value OR given alpha and a corresponding confidence interval

Hypothesis Testing The second type of inferential statistics Hypothesis testing is a statistical method used to make comparisons between a single sample and a population, or between 2 or more samples. The result of a statistical hypothesis test is a probability, called a p-value, of obtaining the results (or more extreme results) from tests of samples, if the results really weren’t true in the population.

Commonly Used Statistical Tests for quantitative data (i. e. comparing means): § Two groups: t-test (paired or 2 -sample) § Two or more groups (ANOVA: analysis of variance) Tests for categorical (nominal, ordinal) data (i. e. comparing proportions): § Chi-square, Fisher’s exact test Tests for association between two quantitative variables: § Correlation and regression

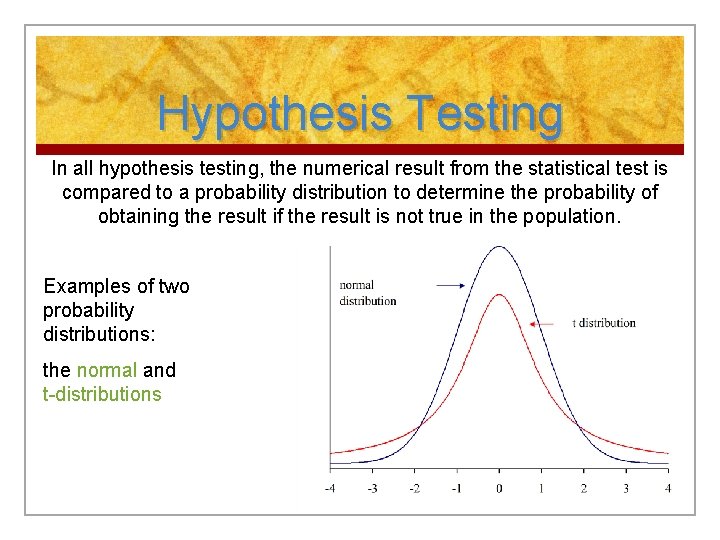
Hypothesis Testing In all hypothesis testing, the numerical result from the statistical test is compared to a probability distribution to determine the probability of obtaining the result if the result is not true in the population. Examples of two probability distributions: the normal and t-distributions

Steps in Statistical Hypothesis Testing 1. Formulate null and research hypotheses 2. Set alpha error (Type I error) and beta error (Type II error) 3. Compute statistical test and determine statistical significance 4. Draw conclusion

Step 1: Formulate Null and Research Hypotheses Null Hypothesis (H 0): There is no difference between groups; there is no relationship between the independent and dependent variable(s). Research Hypothesis (HR): There is a difference between groups; there is a relationship between the independent and dependent variable(s).

Directional vs Non-directional Hypotheses Null and research hypotheses are either non-directional (two-tailed) or directional (one-tailed): Non-directional (two-tailed): H 0: Drug A = Drug B HR: Drug A Drug B Directional (one-tailed): H 0: Drug A Drug B HR: Drug A > Drug B or H 0: Drug A Drug B HR: Drug A < Drug B

Example: Directional vs Non-directional Research question: Does age of onset of paranoid schizophrenia differ for males and females? Non-directional (two-tailed): H 0: Male Age = Female Age HR: Male Age Female Age Directional (one-tailed): H 0: Male Age Female Age HR: Male Age > Female Age (or the opposite)

Step 2: Set Alpha (Type I) and Beta (Type II) Errors Alpha ( ) is the level of significance in hypothesis testing: Alpha is a probability specified before the test is performed. Alpha is the probability of rejecting the null hypothesis when it is true. By convention, typical values of alpha specified in medical research are 0. 05 and 0. 01. Alphas have corresponding critical values, the same ones used to calculate confidence intervals – 0. 05/1. 96, 0. 01/2. 575

Step 2: Set Alpha (Type I) and Beta (Type II) Errors Beta ( ) is the probability of accepting the null hypothesis when it is false. Typical values for beta are 0. 10 to 0. 20 Beta is directly related to the power of a statistical test: Power is the probability of correctly rejecting the null hypothesis when it is false. Power = 1 - Beta A type II error occurs when a false null hypothesis is accepted.

P-values are the actual probabilities calculated from a statistical test, and are compared against alpha to determine whether to reject the null hypothesis or not. Example: alpha = 0. 05; calculated p-value = 0. 008; reject null hypothesis alpha = 0. 05; calculated p-value = 0. 110; do not reject null hypothesis A type I error occurs when a true null hypothesis is rejected.

Possible Outcomes in Statistical Testing

Post treatment mortality in CABG/PTCA study: What are the null and alternative hypotheses for a two-tailed test? Null Hypothesis (H 0) There is no difference in posttreatment mortality between the CABG and PTCA groups (the post treatment mortality is equal, i. e. P 1 = P 2) Research Hypothesis (HR) There is a difference in posttreatment mortality between the CABG and PTCA groups (the post treatment mortality is not equal, i. e. P 1 P 2)

Hypothesis Testing Step 3 Compute statistical test and determine statistical significance • Calculations for statistical tests are different depending on the type of test • All involve determining a value of a test statistic that is then converted to a probability of obtaining that test statistic if the null hypothesis is true. • The value of a test statistic is determined from the measurement being tested, and the variability of the measurement in the sample (the SE of the measurement).

Example of a statistical test: two-sample t test Does age of onset of paranoid schizophrenia differ for males and females? H 0: Male Age = Female Age HR: Male Age Female Age Male Female Test statistic: n 12 12 mean age 26. 8 29. 6 SD 5. 8 6. 2

Example of a statistical test: two-sample t test Does age of onset of paranoid schizophrenia differ for males and females? calculated test statistic: t = -1. 142 Critical value of t for alpha = 0. 05: + 1. 960 The computed value of t does not exceed the critical value so the null hypothesis of no difference in age is not rejected (the p value is greater than 0. 05) Conclusion: The mean age of onset is not different for males versus females

Is the post treatment mortality different for patients receiving CABG compared to patients receiving PTCA? There a number of statistical tests that can be used: 2 examples are 1) chi-square test, or 2) z test for proportions. The resulting p values will be the same regardless of the test used. The researchers used a z test: the p value from the test was 0. 3508. If alpha = 0. 05, what did they conclude?

Is the post treatment mortality different for patients receiving CABG compared to patients receiving PTCA? The p value is 0. 3508… this is >0. 05, so the conclusion from the study is that there is no difference If there is truly no difference between CABG and PTCA, the probability of obtaining the difference of 0. 6% is ~35%

Hypothesis Testing Step 4 Draw conclusion about the population based on the results of the statistical test on the sample Statistical conclusion: the results either are or are not statistically significant……… BUT You need to interpret the results in a meaningful (and not just statistical) way

Principles for Statistical Significance 1. The size of a p value does not indicate importance of the result. 2. Interpret nonsignificance cautiously. a. finding no difference may be important b. statistically nonsignificant clinically unimportant 3. Results may be statistically significant but clinically trivial.

P Values vs. Confidence Intervals • There is a direct relationship between levels of alpha set for a statistical test and the level set for constructing a confidence interval. For example, alpha = 0. 05 for a 2 -sided statistical test is equivalent to a 95% confidence interval

P Values vs. Confidence Intervals Statistical significance can be obtained from a confidence interval as well as a hypothesis test AND Confidence intervals convey more information than p values For this reason, most medical journals now prefer that results be presented with confidence intervals rather than p values. If the NULL VALUE for a statistical hypothesis test using alpha = 0. 05 is contained within the 95% confidence interval, we can conclude NO statistical significance at alpha = 0. 05 without doing the hypothesis test:

P Values vs. Confidence Intervals Example: For differences between means or proportions, the null hypothesis is that the difference is equal to zero: If the 95% CI includes the value zero, the differences are not statistically significant at alpha = 0. 05. For the test comparing the ages of males and females for onset of paranoid schizophrenia, the null hypothesis is that the difference in age is zero years.

P Values vs. Confidence Intervals Example: Male Female n 12 12 mean age 26. 8 29. 6 SD 5. 8 6. 2 The difference in age obtained from the sample is: 26. 8 -29. 6 = -2. 8 years The standard error of the difference is 2. 45 (calculation not shown) The 95% confidence interval is: -2. 8 +/- 2(2. 45) = -2. 8 +/- 4. 9 = -7. 7 to 2. 1 years

P Values vs. Confidence Intervals The 95% confidence interval is: -2. 8 +/- 2(2. 45) = -2. 8 +/- 4. 9 = -7. 7 to 2. 1 years This means that the true population mean difference in age is somewhere between males being 7. 7 years younger to males being 2. 1 years older than females The 95% CI includes 0 years, so there is no statistically significant difference in age. In addition, we have information about the precision of our estimate of the difference, which cannot be obtained from p values alone. Note: This is a relatively wide confidence interval because the sample size is small

P Values vs. Confidence Intervals For the CABG/PTCA result: The 95% CI is – 0. 6% to 1. 7% We can be 95% confident that the true difference in mortality between CABG and PTCA is between – 0. 6% and +1. 7% This confidence interval contains the value zero; therefore, we could have concluded that the mortality is not different based on the confidence interval alone.

P Values vs. Confidence Intervals For ratio variables, such as relative risk and odds ratio, the value one represents equality. The null hypothesis is that the ratio is equal to one: If the 95% CI includes the value one, the difference is not statistically significant at alpha = 0. 05.