AZ INFORMATIKA LOGIKAI ALAPJAI INCK 401 Elad Dr

AZ INFORMATIKA LOGIKAI ALAPJAI INCK 401 Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2014/2015. I. félév 2. gyakorlat

Tartalom � Logikai műveletek - ismétlés � Formalizálás � A logika feladata � Példák helyes és helytelen következtetésekre � Feladatok az induktív definíció alkalmazására

Érvelések

Következtetés Premissza: � a következtetés valamely kiinduló állítása (lásd kicsit később) � azon állítások, amelyek igazságának feltételezése mellett kívánjuk a konklúzió igazságát biztosítani Konklúzió: � a következtetés eredményeként kapott állítás � a következtetés kimenete (outputja)

A logika feladata A premisszák és a konklúzió közötti összefüggés tanulmányozása. Helyes következtetés: ha a premisszák igaz volta esetén a konklúzió is igaz. Például: � premissza 1: Erika Sándornak a felesége. � premissza 2: Katalin Sándornak az édesanyja. � konklúzió: Katalin Erikának az anyósa. � pótpremissza: Ha x y-nak a felesége és z y-nak az édesanyja, akkor z x-nek az anyósa.

Helytelen (hibás) következtetés (P 1): Ha a benzin elfogyott, az autó megáll. (P 2): Nem fogyott el a benzin. (K): Az autó nem áll meg. Betűk használatával (mint a matematikában): � Ha A, akkor B. � Nem A. � Nem B.

Logika - Hofi p: //www. youtube. com/watch? v=AEZikzeji 2 A

Következtetés logikai vizsgálata logikai szavak: � nem ¬ negáció � és ∧ konjunkció � vagy ∨ diszjunkció � ha… akkor… ⊃ implikáció � minden ∀ univerzális kvantor � van ∃ egzisztenciális kvantor a mondatrészek, szavak jelentése közömbös, helyettük: � atomi formulák � termek

Formalizálás Állítás: Egy kijelentő mondat állítás, ha egyértelmű információt hordoz és igazságértékkel bír. Egy állítás igaz, ha az információtartalom a valóságnak megfelelő, egyébként hamis, függetlenül tudásunktól.

Ítélet (állítás) Ítéleten olyan értelmes, zárt kijelentő mondatot értünk, amely egyértelműen igaz vagy hamis. A fenti definícióban az egyértelműségi követelmény klasszikus és bővebb megfogalmazásban a következő feltételek teljesülését jelenti: � � � Egy ítélet nem lehet egyszerre igaz és hamis. (ellentmondástalanság elve) Nincs olyan ítélet, amely se nem igaz, se nem hamis. (kizárt harmadik elve) Ha egy ítélet nem hamis (nem igaz, hogy nem igaz), akkor az az ítélet igaz. (kettős tagadás elve) Összefoglalva, ítélet vagy igaz és ekkor nem hamis, vagy hamis és ekkor nem igaz, más lehetőség (másféle ítélet) nincs.

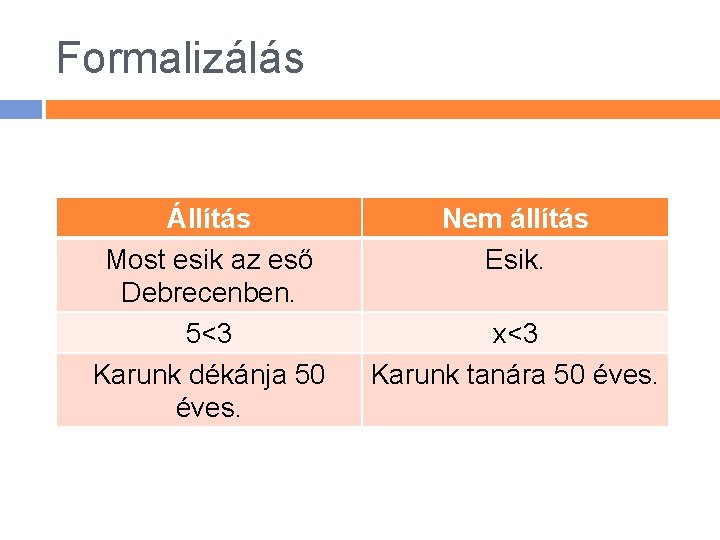
Formalizálás Állítás Most esik az eső Debrecenben. 5<3 Karunk dékánja 50 éves. Nem állítás Esik. x<3 Karunk tanára 50 éves.

Formalizálás Gyakran az egyszerű állítások szerkezetét is fel kell tárnunk: Dezső postás. Amália és Bella testvérek. Az Erzsébet híd összeköti Budát Pesttel. predikátum + objektumnevek

A negáció ¬p 0 1 1 0 igazságtáblázata Tipikus természetes nyelvi alakja: 'Nem igaz, hogy. . . ' Legyen A∈Form. ¬A kiolvasása: � Nem igaz, hogy A. � Non A. � Negáció A. p Kettős negáció törvénye: ¬¬A⇔A

Példák A: „Alfréd diák. ” Alfréd nem diák: ¬A É: „Éva szőke. ” Éva nem szőke: ¬É

A konjunkció ∧ 0 1 0 0 0 1 igazságtáblázata Tipikus természetes nyelvi alakja: . . . és. . . Legyen A, B∈Form. (A∧B) kiolvasása: � A és B. � A konjunkció B.

A konjunkció tulajdonságai Felcserélhető (kommutatív): (A∧B)⇔(B∧A) Csoportosítható (asszociatív): (A∧(B∧C))⇔((A∧B)∧C) Idempotens: (A∧A)⇔A (A∧B)⊨A, (A∧B)⊨B Az ellentmondás törvénye: ⊨¬(A∧¬A)

Példák A: „Amália kertész. ” B: „Bella kertész. ” Amália és Bella kertészek: A∧B P: „Péntek van. ” L: „Logikát tanulunk. ” Péntek van és logikát tanulunk: P∧L

A diszjunkció ∨ 0 1 0 0 1 1 igazságtáblázata Tipikus természetes nyelvi alakja: . . . vagy. . . (megengedő értelemben) Legyen A, B∈Form. (A∨B) kiolvasása: � A vagy B. � A diszjunkció B.

A diszjunkció tulajdonságai Felcserélhető (kommutatív): (A∨B)⇔(B∨A) Csoportosítható (asszociatív): (A∨(B∨C))⇔((A∨B)∨C) Idempotens: (A∨A)⇔A A⊨(A∨B) {(A∨B), ¬A}⊨B A kizárt harmadik törvénye. ⊨(A∨¬A)

Példák E: „Esik az eső. ” F: „Fúj a szél. ” Esik az eső, vagy fúj a szél: E∨F S: „Sikeres félévet zárok logikából” Sikeres félévet zárok logikából vagy nem zárok sikeres félévet logikából: S∨¬S

Az implikáció ⊃ 0 1 1 1 0 1 igazságtáblázata Tipikus természetes nyelvi alakja: Ha. . . , akkor. . . Legyen A, B∈Form. (A⊃B) kiolvasása: � Ha A, akkor B. � Amennyiben A, úgy B. � A implikáció B. � A implikálja B-t.

Az implikáció tulajdonságai ⊨(A⊃A) Modus ponens (leválasztási szabály): {(A⊃B), A}⊨B Modus tollens (indirekt cáfolás sémája): {(A⊃B), ¬B}⊨¬A Láncszabály: {(A⊃B), (B⊃C)}⊨(A⊃C) Redukció ad abszurdum: {(A⊃B), (A⊃¬B)}⊨¬A ¬A⊨(A⊃B) B⊨(A⊃B)

Az implikáció tulajdonságai Áthelyezési törvény: ((A∧B)⊃C)⇔(A⊃(B⊃C)) Kontrapozíció: (A⊃B)⇔(¬B⊃¬A) (A⊃¬A)⊨¬A (¬A⊃A)⊨A (A⊃(B⊃C))⇔((A⊃B)⊃(A⊃C)) ⊨(A⊃(¬A⊃B)) ((A∨B)⊃C)⇔((A⊃C)∧(B⊃C))

Példák M: „Megtanulom a leckét. Ö: „Ötösre felelek. ” Ha megtanulom a leckét, akkor ötösre felelek: M⊃Ö E: „Esik a hó. ” T: „Tél van. ” Ha esik a hó, akkor tél van: E⊃T

≡ 0 1 0 1 0 igazságtáblázata Tipikus természetes nyelvi alakja: . . . akkor és csak akkor, ha. . . Legyen A, B∈Form. (A≡B) kiolvasása: 1 A (materiális) ekvivalencia � A akkor és csak akkor, ha B. � A ekvivalens B(-vel). � A materiálisan ekvivalens B(-vel). A materiális jelzőt gyakran elhagyjuk. Szerepeltetését pusztán az indokolja, hogy megkülönböztessük a (materiális) ekvivalencia műveletét a logikai ekvivalencia relációjától.

A (materiális) ekvivalencia tulajdonságai ⊨(A≡A) ⊨¬(A≡¬A) Kommutatív: (A≡B)⇔(B≡A) Asszociatív: (A≡(B≡C))⇔((A≡B)≡C)

Példák P: „A kettő prímszám. ” O: „Hat osztható hárommal. ” A kettő prímszám akkor és csak akkor, ha a hat osztható hárommal: P≡O

Formalizálás Univerzális kvantor: Amália mindegyik testvére lány. Egzisztenciális kvantor: Amáliának van testvére.

A konjunkció és a diszjunkció Kétoldali disztributivitás: � (A∨(B∧C))⇔((A∨B)∧(A∨C)) (A diszjunkció disztributív a konjunkcióra nézve. ) � (A∧(B∨C))⇔((A∧B)∨(A∧C)) (A konjunkció disztributiv a diszjunkcióra nézve. ) Elnyelési tulajdonság: � (A∧(B∨A))⇔A � (A∨(B∧A))⇔A

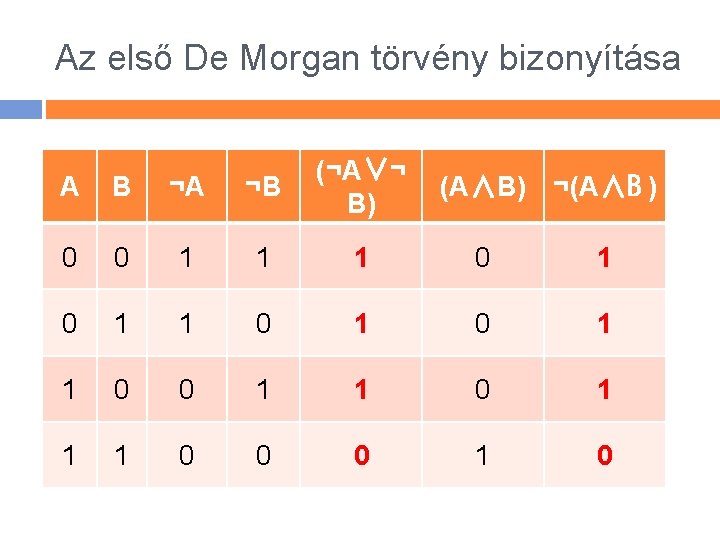
A konjunkció és a diszjunkció De Morgan törvények Mit állítunk akkor, amikor egy konjunkciót tagadunk? � ¬(A∧B)⇔(¬A∨¬B) Mit állítunk akkor, amikor egy diszjunkciót tagadunk? � ¬(A∨B)⇔(¬A∧¬B)

Az első De Morgan törvény bizonyítása A B ¬A ¬B (¬A∨¬ B) 0 0 1 1 1 0 1 0 1 1 0 0 1 1 1 0 0 0 1 0 (A∧B) ¬(A∧B )

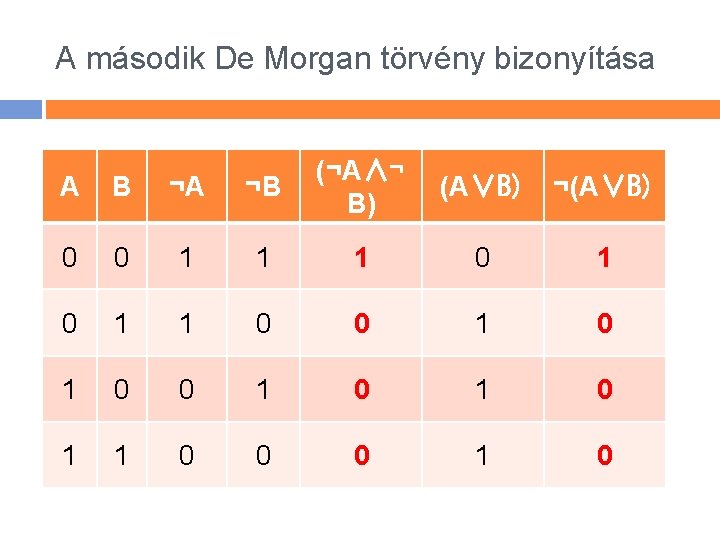
A második De Morgan törvény bizonyítása A B ¬A ¬B (¬A∧¬ B) 0 0 1 1 1 0 0 1 0 1 0 1 1 0 0 0 1 0 (A∨B) ¬(A∨B)

Nulladrendű nyelv – Formalizálás 1. 2. 3. 4. 5. Péter nem ment haza. Éva nem szőke. Nem igaz, hogy Péter nem ment haza. Nem áll, hogy nem igaz, hogy Éva nem szőke. Péter vagy nem ment haza, vagy nem maradt otthon, de nem áll, hogy otthon van.

Elsőrendű nyelv - Formalizálás 1. 2. 3. 4. Gábor pék. Ha Gábor pék, akkor Kriszta is az. Vannak pékek. Minden ember pék.

Elsőrendű nyelv - Formalizálás K(x) jelentse azt, hogy „x – használtautó kereskedő” T(x) jelentse azt, hogy „x – tisztességes ember” Mit jelentenek ekkor a a) ∃x. K(x) b) ∀x(K(x) ⊃¬T(x)) c) ∃x(K(x)∧T(x)) d) ∃x(T(x) ⊃K(x)) formulák?

Az alábbi állításokban vezessünk be új változókat és jelöljük ki a kvantorokat! Használjuk szükség szerint a negációjelet! 1. 2. 3. 4. 5. 6. 7. 8. Mindenki szeret valakit. Mindenkit szeret valaki. Mindenki szeret mindenkit. Mindenki szereti önmagát. Van, aki mindenkit szeret. Van, akit mindenki szeret. Van, aki szereti önmagát. Senki sem szeret mindenkit.

Induktív definíció I. Egy sajátos és nagyon megbízható definíciós módszer. Elsősorban halmazok, függvények és sorozatok definiálására használható. A definíció két fő részből áll: A bázis megadása A szabály, vagy szabályok megadása

Rekurzív (induktív) definíció* A fogalom definíciója olyan, hogy definiáljuk a fogalom egy részfogalmát, részhalmazát, majd a további definíciónál erre a már definiált részhalmazra is hivatkozunk. Leggyakrabban sorozatok definiálására használjuk, például "a 1 : = 2; an+1 : = 2 an" nem más, mint rekurzív definíció az {an} : = 2 n sorozatra. Így először az első tag mibenlétét (mint a sorozat egy részhalmazát) definiáljuk, majd megmutatjuk, az előző tagok ismeretében hogyan lehet a következőket kiszámolni. *http: //hu. wikipedia. org/wiki/Meghatározás

Rekurzív (induktív) definíció* Az első lépést bázisnak, a másodikat bővítési szabálynak szokás nevezni, és a definíció (általában implicit módon) tartalmaz egy ún. záradékot is, ami azért felelős, hogy más ne tartozzon a fogalom alá. [4] *http: //hu. wikipedia. org/wiki/Meghatározás

[4] Röviden és informálisan tehát az an sorozat rekurzív definíciója: Bázis: A 2 eleme az an sorozatnak. Bővítési szabály: Ha valami eleme az an sorozatnak, akkor a kétszerese is eleme az an sorozatnak. Záradék: Más nem eleme az an sorozatnak.

Példa 1. A hárommal osztható természetes számok halmazát (jelöljük ezt A-val) például megadhatjuk az alábbi induktív definícióval: Bázis: 3 eleme A-nak Bővítési szabály: Ha valami eleme az A-nak, akkor a 3 -mal növelt szám is eleme A-nak.

Példa 2. Az ab- jelsorozatok halmazát az alábbi induktív defínicóval adhatjuk meg: Bázis: a b Bővítési szabályok: X->Xa X->Xb (ahol X tetszőleges jel)

Idenpotencia A �� A = A Kommutativitás A �� B = B �� A Asszociativitás (A �� B) �� C = A �� (B �� C) (A �� B) �� C = A Disztributivitás A �� (B �� C) = (A �� B) �� (A �� C) A �� (B � De Morgan-képletek A�� B �� A�� B http: //www. math. klte. hu/~kovacsa/Halmaz. pdf

Feladatok 1. Adjuk meg az a-val kezdődő és b-re végződő jelsorozatok halmazát induktív definícióval!

Segédletek logikából Dr. Mihálydeák Tamás: � http: //www. inf. unideb. hu/~mihalydeak/Logika_html_2011_11_15. zip � http: //www. inf. unideb. hu/~mihalydeak/Logika_my_twt-treeview. html � http: //www. inf. unideb. hu/~mihalydeak/Inf_log_ea_06_07_1. pdf Dr. Várterész Magda: � http: //www. inf. unideb. hu/~varteres/logika/Logikafo. pdf � http: //www. inf. unideb. hu/~varteres/logika_peldatar/matlog. pdf � http: //www. inf. unideb. hu/~varteres/logika_peldatar/megoldas. pdf Lengyel Zoltán: � http: //www. inf. unideb. hu/~lengyelz/docs/logika. pdf