Anlisis Matemtico I Ing Antonio Crivillero Men Principal

Análisis Matemático I Ing. Antonio Crivillero

Menú Principal n Particiones. n Definición: Integral Definida. n Teorema (Condición Necesaria y suficiente para existencia de ). n Teorema (Condición Suficiente para la existencia de ). n Propiedades Básicas de la Integral Definida n Definición: Media n Teorema (Primer Teorema del Valor Medio del Cálculo Integral). n Teorema (Primer Teorema Fundamental del Cálculo Integral). n Teorema (Regla de Barrow). n Definición: Integral Indefinida. n Aplicaciones Geométricas de la Integral

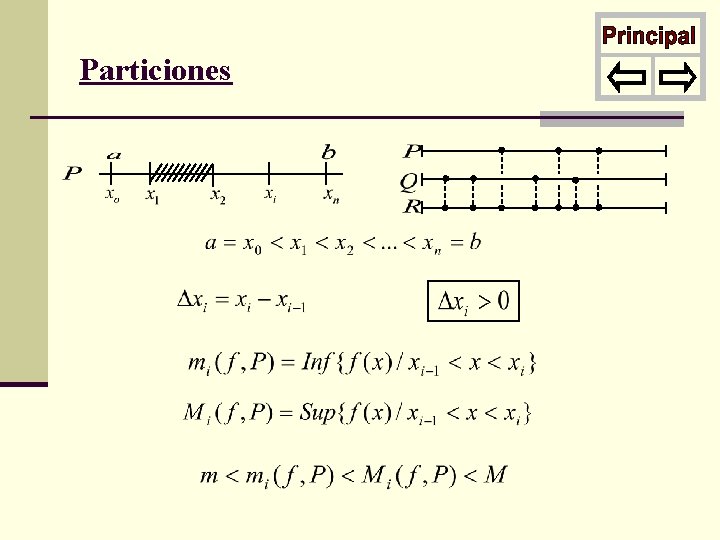
Particiones

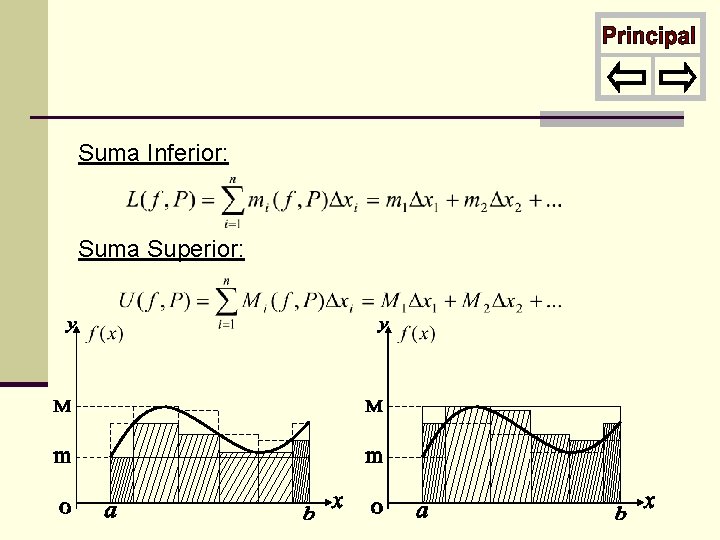
Suma Inferior: Suma Superior:

Propiedades: Si Q es posterior a P

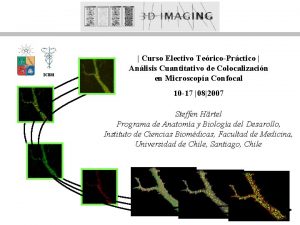
Definición: Integral Definida Sea acotada, diremos que f es integrable sobre [a, b] si y sólo si En este caso se denota y se dice que este número es la integral definida de f sobre [a, b].

Teorema (Condición Necesaria y suficiente para existencia de ) Si f está acotada sobre [a, b], entonces f es integrable sobre ese intervalo si y sólo si para todo existe una partición P de [a, b] tal que: Demostración: Supongamos que para cada. Entonces De donde se sigue que sobre [a, b]. tal que , y f es integrable

Teorema (Condición Necesaria y suficiente para existencia de ) Recíprocamente, supongamos que f es integrable sobre [a, b]. Entonces Por lo tanto es el supremo del conjunto y el ínfimo del conjunto. Por la definición de ínfimo y supremo, para cada existen particiones tales que P/ ínfimos y P/ supremos

Teorema (Condición Necesaria y suficiente para existencia de ) Sumando estas desigualdades, obtenemos Sea , entonces P es un refinamiento tanto de P 1 como de P 2. Por lo tanto,

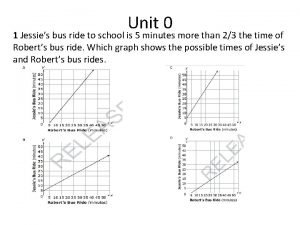
Teorema (Condición suficiente para existencia de ) Si sobre [a, b]. es continua, entonces f es integrable Demostración: La continuidad f continua sobre [a, b] implica que f es uniformemente continua sobre [a, b], y f acotada sobre [a, b], por lo tanto f tiene un máximo y mínimo sobre cada intervalo de [a, b]. Para cada partición P de [a, b] existen que y. tales

Teorema (Condición suficiente para existencia de ) Tenemos entonces La continuidad uniforme de f sobre [a, b] implica que para cada tal que si y se tiene Por lo tanto implica Por el teorema (Condición necesaria y suficiente para la existencia de ) entonces, se sigue que f es integrable. -

Propiedades Básicas de la Integral Definida A continuación enunciamos una serie de propiedades básicas de la integral definida. Si f y g son integrables en [a, b], entonces f + g es integrable en [a, b] y Si f y g son integrables en [a, b], y f(x) ≤ g(x) para todo Entonces

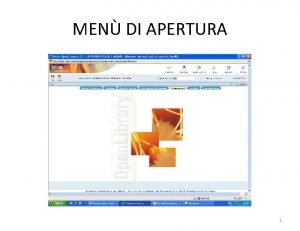
Propiedades Básicas de la Integral Definida Si f es integrable en [a, b], entonces | f | es integrable en [a, b] y Si f es integrable en el intervalo J y si entonces con a<b Si f es integrable en [a, b] y c una constante, entonces cf es integrable en [a, b] y

Definición de Media Dado un conjunto de n números , la media o promedio aritmético de ellos está dado por La integral definida nos permite extender este concepto a los valores de una función sobre un intervalo.

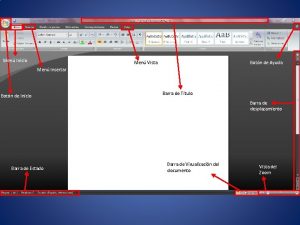
Definición de Media Definición: Si f es integrable en un intervalo [a, b], la media de f sobre [a, b] se define como Esta media tiene la siguiente interpretación geométrica: si Es el área bajo la gráfica de la función f, como

Definición de Media Esto quiere decir que es la altura de un rectángulo con base b-a cuya área es El Teorema siguiente establece un resultado relacionado con la media de una función continua.

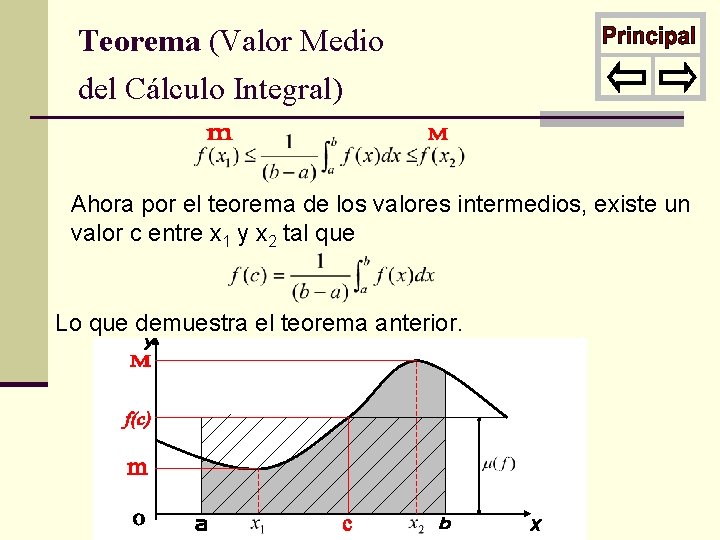
Teorema (Valor Medio del Cálculo Integral) Sea tal que continua. Entonces existe un número . Demostración: Como f es continua existen tales que para todo entre a y b tenemos que y dividiendo por (b - a) . Integrando

Teorema (Valor Medio del Cálculo Integral) Ahora por el teorema de los valores intermedios, existe un valor c entre x 1 y x 2 tal que Lo que demuestra el teorema anterior.

Teorema (Teorema fundamental del Cálculo Integral) Sea continua y sea definida por . Entonces G es derivable en (a, b) y Para todo Demostración: Sea que y tal que por un lado . Queremos ver

Teorema (Teorema fundamental del Cálculo Integral) Usando esto último tenemos que Y aplicando el teorema del valor medio del cálculo integral del último límite podemos escribir Donde está entre Cuando y , y como f es continua y tenemos

Teorema (Primer teorema fundamental del Cálculo Integral) Esto es, lo que completa la demostración.

Teorema (Regla de Barrow) Sea f continua en un intervalo [a, b]. Si F es derivable en [a, b] y si para todo , entonces Demostración: Como F es primitiva de f, entonces F’(x)=f(x) Sea G función integral Por el primer Teorema fundamental G’=f sobre [a, b]. Por lo tanto G’=F’ sobre [a, b], lo que indica que G y F difieren en una constante, esto es,

Teorema (Regla de Barrow) Como , de donde , por lo tanto

Definición: Integral Indefinida Si F es una función primitiva de f, se llama integral indefinida de f a la expresión: donde, f es la función integrando, es el elemento de integración y es el símbolo integral. Como la expresión no determina un único resultado, da lugar a dos distintas interpretaciones: n es una primitiva arbitraria de f. n es el conjunto formado por todas las primitivas de f.

Aplicaciones Geométricas de la Integral Longitud de una curva Área entre dos curvas

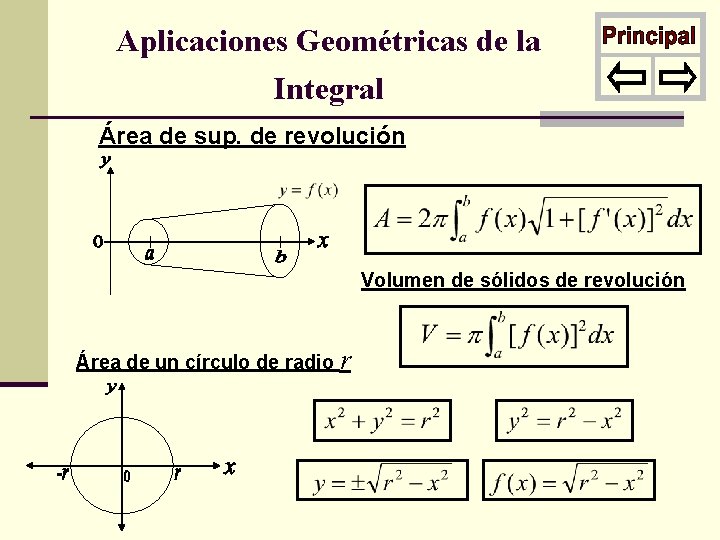
Aplicaciones Geométricas de la Integral Área de sup. de revolución Volumen de sólidos de revolución Área de un círculo de radio r