Anlise de Algoritmos Estruturas de Dados e Algoritmos

Análise de Algoritmos Estruturas de Dados e Algoritmos II Prof. Ricardo Linden Análise de Algoritmos

Notação para análise de complexidade ð Quando estamos analisando a complexidade de um algoritmo, estamos interessados mais no comportamento geral do que nos pequenos detalhes (que variam de máquina para máquina) ð Nós gostaríamos de saber quão rápido a complexidade de um algoritmo cresce conforme aumentamos um parâmetro do problema (n - normalmente o tamanho da entrada). ð O que realmente nos interessa é a eficiência assintótica dos algoritmos em máquinas que operam no modelo de acesso aleatório Análise de Algoritmos 2

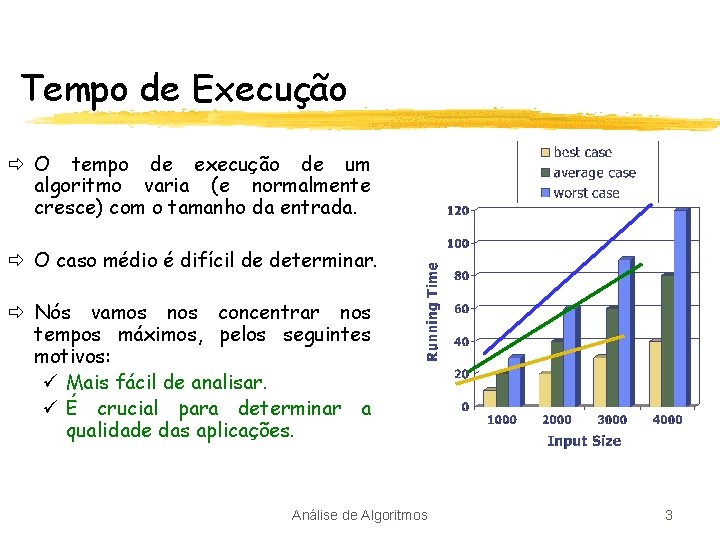
Tempo de Execução ð O tempo de execução de um algoritmo varia (e normalmente cresce) com o tamanho da entrada. ð O caso médio é difícil de determinar. ð Nós vamos nos concentrar nos tempos máximos, pelos seguintes motivos: ü Mais fácil de analisar. ü É crucial para determinar a qualidade das aplicações. Análise de Algoritmos 3

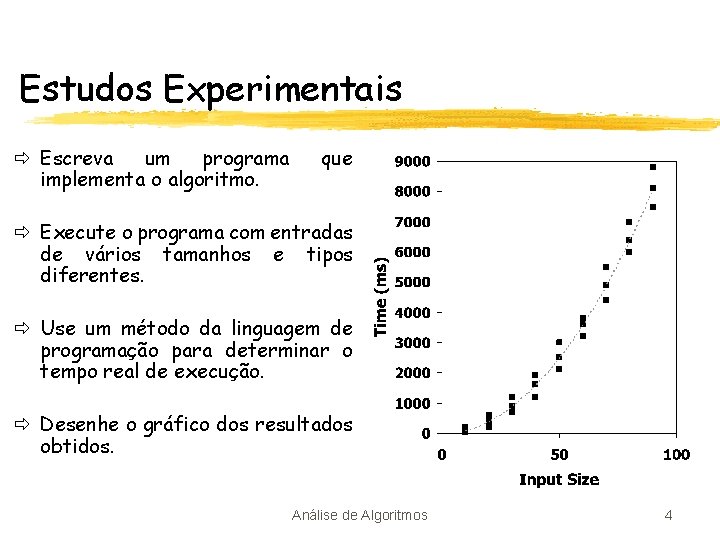
Estudos Experimentais ð Escreva um programa implementa o algoritmo. que ð Execute o programa com entradas de vários tamanhos e tipos diferentes. ð Use um método da linguagem de programação para determinar o tempo real de execução. ð Desenhe o gráfico dos resultados obtidos. Análise de Algoritmos 4

Análise Teórica ð Leva em consideração todos os tipos de entrada possíveis. ð Permite que avaliemos a velocidade do algoritmo de forma independente do ambiente de hardware e software Análise de Algoritmos 5

Operações Primitivas ð Computações básicas realizadas por um algoritmo. ð Definição exata não é importante ð Contadas como executando em tempo unitário, apesar de obviamente serem diferentes. ð Exemplos: ü ü ü Avaliando uma expressão. Atribuindo um valor para ma vaiável. Chamando uma função Escrevendo na tela Etc. Análise de Algoritmos 6

Contando Operações Primitivas ð Inspecionando o código, nós podemos determinar o número máximo de operações executados por um algoritmo, como função do tamanho da entrada. int array. Max(int A[], int n) { current. Max = A[0]; for(i=1; i<n; i++) { if (A[i] current. Max) current. Max A[i]; } return current. Max # operations 1 1+ (repete n-1 vezes) [ teste(1) e incremento (1) 1 1 ] 1 Total } Análise de Algoritmos (n-1)*4 + 3 = 4 n - 1 7

Estimando o tempo de execução ð O algoritmo array. Max executa 4 n 1 operações primitivas no pior caso ð Definimos: ü a Tempo levado pela operação primitiva mais rápida ü b Tempo levado pela operação primitiva mais lenta ð Seja T(n) o verdadeiro tempo de execução de pior caso da função array. Max calculado anteriormente. Nós temos: a (4 n 1) T(n) b(4 n 1) ð Logo, o tempo de execução T(n) é limitado por duas funções lineares Análise de Algoritmos 8

Taxa de crescimento do tempo de execução ð Mudando o ambiente de hardware/ software ü Afeta T(n) por um fator constante ü Não altera a taxa de crescimento de T(n) ð A taxa de crescimento linear de T(n) é uma propriedade intrínseca do algoritmo array. Max Todo algoritmo tem uma taxa de crescimento que lhe é intrínseca - o que varia de ambiente para ambiente é o apenas o tempo absoluto de cada execução, que é absolutamente dependente de fatores como poder de processamento Análise de Algoritmos 9

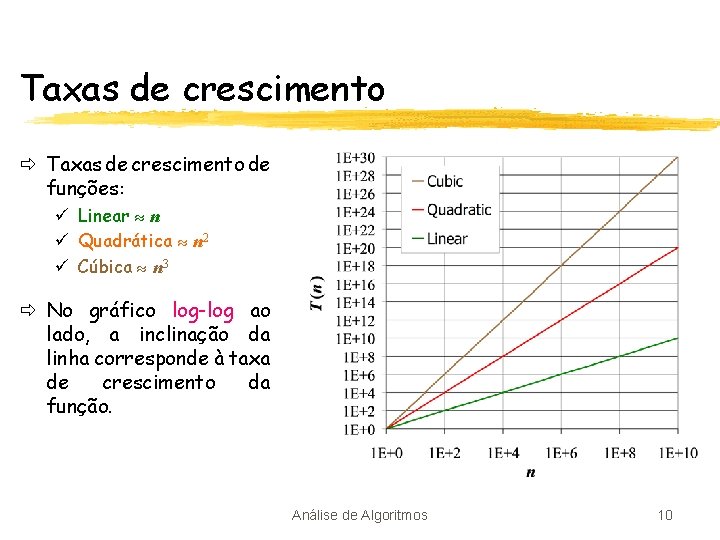
Taxas de crescimento ð Taxas de crescimento de funções: ü Linear n ü Quadrática n 2 ü Cúbica n 3 ð No gráfico log-log ao lado, a inclinação da linha corresponde à taxa de crescimento da função. Análise de Algoritmos 10

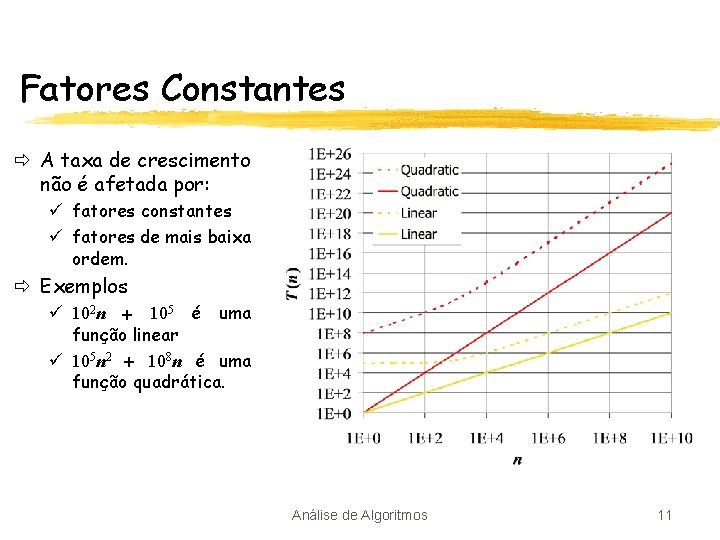
Fatores Constantes ð A taxa de crescimento não é afetada por: ü fatores constantes ü fatores de mais baixa ordem. ð Exemplos ü 102 n + 105 é uma função linear ü 105 n 2 + 108 n é uma função quadrática. Análise de Algoritmos 11

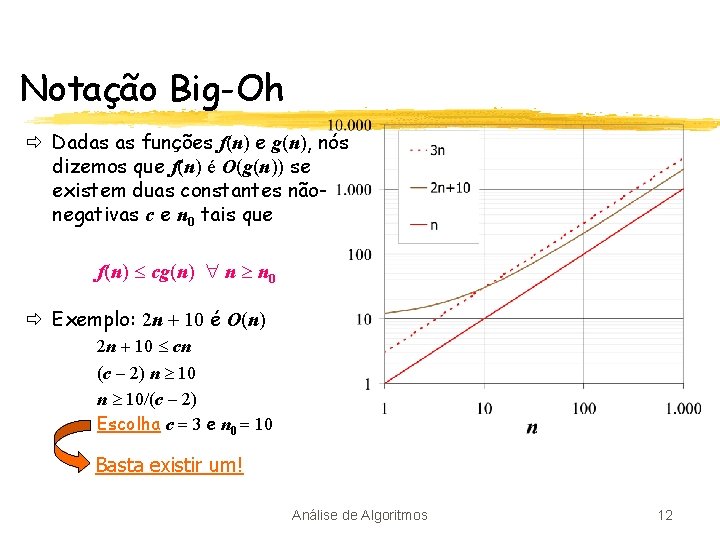
Notação Big-Oh ð Dadas as funções f(n) e g(n), nós dizemos que f(n) é O(g(n)) se existem duas constantes nãonegativas c e n 0 tais que f(n) cg(n) n n 0 ð Exemplo: 2 n + 10 é O(n) 2 n + 10 cn (c 2) n 10/(c 2) Escolha c = 3 e n 0 = 10 Basta existir um! Análise de Algoritmos 12

Notação Big-Oh Isto é, uma função f(n) é O(g(n)) se após um determinado ponto n 0 f(n) não é maior que cg(n) Análise de Algoritmos 13

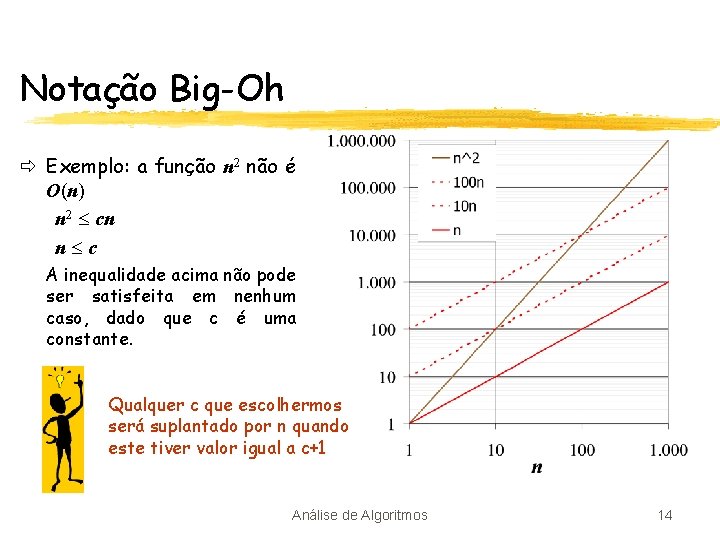
Notação Big-Oh ð Exemplo: a função n 2 não é O(n) n 2 cn n c A inequalidade acima não pode ser satisfeita em nenhum caso, dado que c é uma constante. Qualquer c que escolhermos será suplantado por n quando este tiver valor igual a c+1 Análise de Algoritmos 14

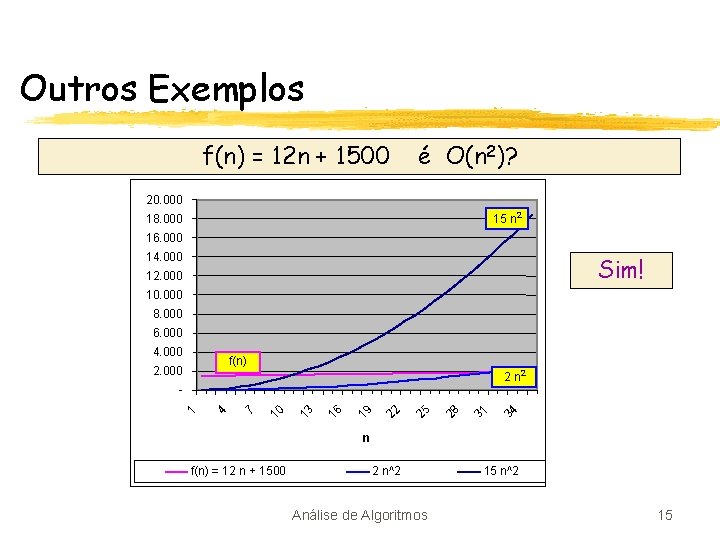
Outros Exemplos f(n) = 12 n + 1500 é O(n 2)? 20. 000 15 n 2 18. 000 16. 000 14. 000 Sim! 12. 000 10. 000 8. 000 6. 000 4. 000 f(n) 2. 000 31 28 25 22 19 16 13 10 7 4 1 - 34 2 n f(n) = 12 n + 1500 2 n^2 Análise de Algoritmos 15 n^2 15

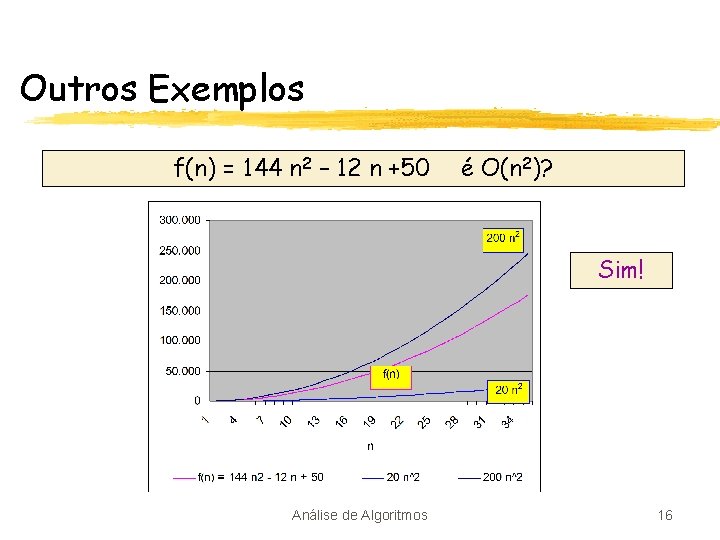
Outros Exemplos f(n) = 144 n 2 – 12 n +50 é O(n 2)? Sim! Análise de Algoritmos 16

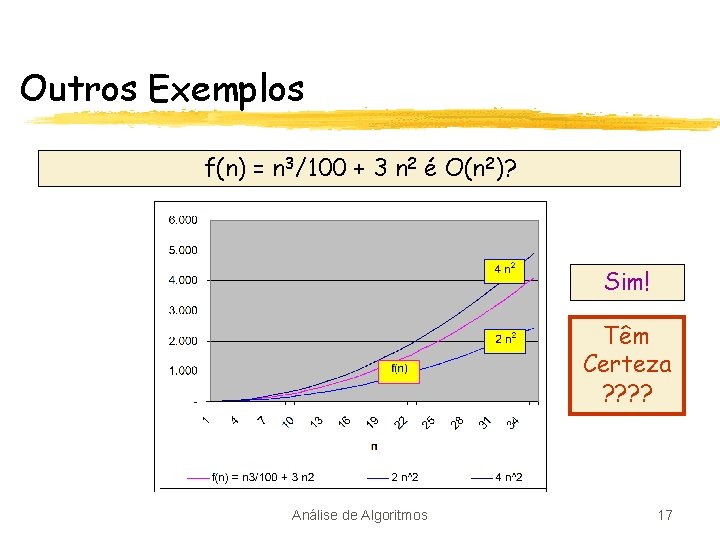
Outros Exemplos f(n) = n 3/100 + 3 n 2 é O(n 2)? Sim! Têm Certeza ? ? Análise de Algoritmos 17

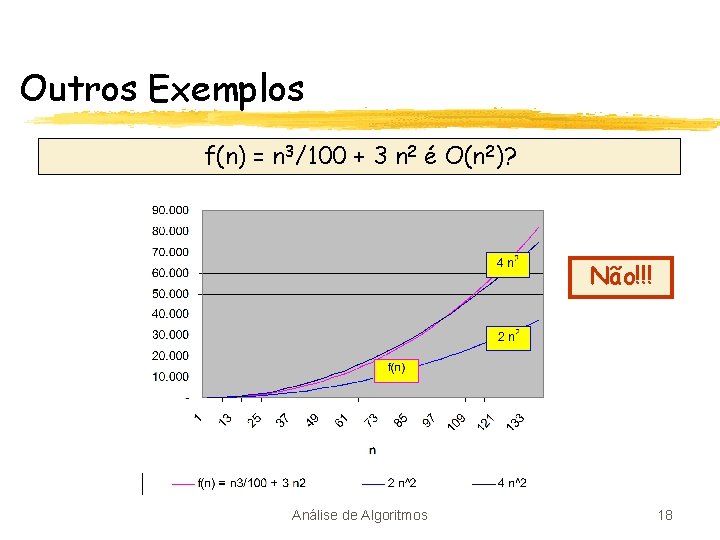
Outros Exemplos f(n) = n 3/100 + 3 n 2 é O(n 2)? Não!!! Análise de Algoritmos 18

Mais exemplos ð 6 n 4 + 12 n 3 + 12 O(n 4) O(n 5) O(n 3) ð 3 n 2 + 12 n log n O(n 2) O(n 5) O(n) ð 5 n 2 + n (log n)2 + 12 O(n 2) O(n 5) ð log n + 4 O(log n) Análise de Algoritmos O(n) 19

Big-Oh e taxa de crescimento ð A notação big-Oh fornece um limite superior para a taxa de crescimento da função ð A afirmação “f(n) é O(g(n))” significa que a taxa de crescimento de f(n) não é maior que a taxa de crescimento de g(n) ð Nós usamos a notação big-Oh para ordenar as funções de acordo com sua taxa de crescimento g(n) cresce mais f(n) cresce mais Mesma taxa f(n) é O(g(n)) ? g(n) é O(f(n)) ? Sim Não Sim Análise de Algoritmos 20

Classes de Funções ð Seja {g(n)} o conjunto de funções que são O(g(n)) ð Nós temos então o seguinte: {n} {n 2} {n 3} {n 4} {n 5} … (note que cada um dos conjuntos está estritamente contido no seguinte da hierarquia) {n 3} {n 2} {n} Análise de Algoritmos 21

Classes de Funções ð Isto quer dizer que toda função O(n) também é O(n 2), toda função O(n 2) também é O(n 3), e assim por diante. ð Isto é uma decorrência óbvia do fato de n ser sempre não negativo e na verdade nós estarmos procurando valores grandes de n (n ) Análise de Algoritmos 22

Muita atenção ð O sinal de igualdade aqui não tem o significado habitual!!! 10 n 2 + 10 log n = O(n 2) 2 n 2 – 3 = O(n 2) 10 n 2 + 10 log n = 2 n 2 – 3 Análise de Algoritmos 23

Regras do cálculo Big-Oh ð Se f(n) é uma função polinomial de grau d, então f(n) é O(nd), isto é: ü Descarte termos de menor ordem ü Descarte termos constantes. ð Use o menor conjunto possível. ü Diga “ 2 n é O(n)” em vez de “ 2 n é O(n 2)” ð Use a expressão mais simples da classe ü Diga “ 3 n + 5 é O(n)” em vez de “ 3 n + 5 é O(3 n)” Análise de Algoritmos 24

Análise ð operações consecutivas - some seus tempos: for ( int x = 1; x < N; x++ O(N) ) <operação qualquer>; for ( int x = 1; x < N; x++ ) for ( int y = 1; O(N y <2) N; y++ ) <operação qualquer>; ð tempo total : N + N 2 O(N 2) Algorithm Analysis 25

Análise ð condicional - Nunca maior que o tempo do teste somando ao maior dos tempos dos blocos de operações do condicional if ( x == y ) do. Something(); else do. Something. Else(); Big-Oh de do. Something() ou de do. Something. Else() (a maior) ð Chamadas de função : conte o tempo de execução da função (e não 1, que é o tempo da chamada) Análise de Algoritmos 26

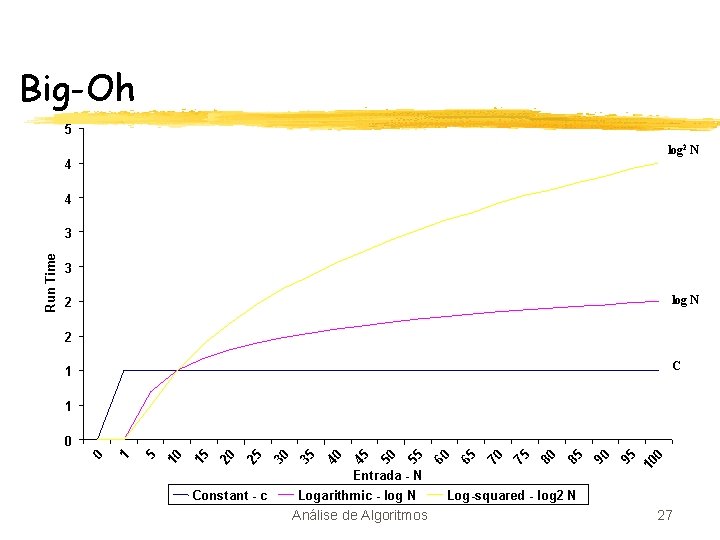
Big-Oh 5 log 2 N 4 4 3 log N 2 2 C 1 1 Constant - c Logarithmic - log N Análise de Algoritmos 0 95 10 Entrada - N 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 1 0 0 Run Time 3 Log-squared - log 2 N 27

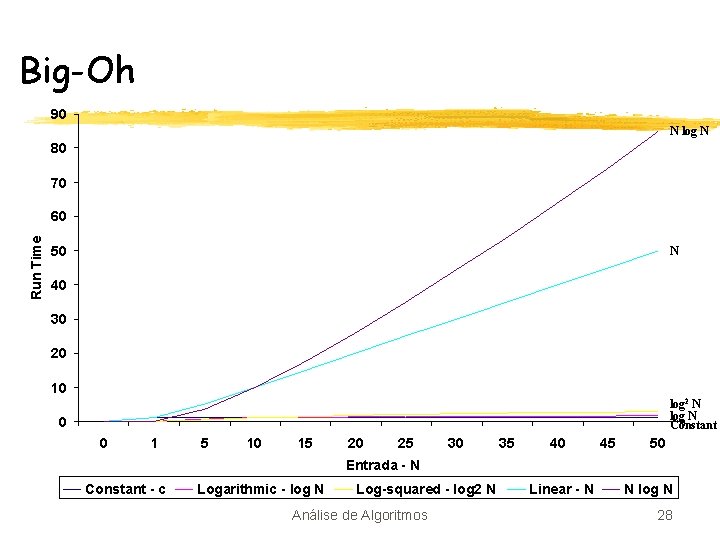
Big-Oh 90 N log N 80 70 Run Time 60 50 N 40 30 20 10 log 2 N log N Constant 0 0 1 5 10 15 20 25 30 35 40 45 50 Entrada - N Constant - c Logarithmic - log N Log-squared - log 2 N Análise de Algoritmos Linear - N N log N 28

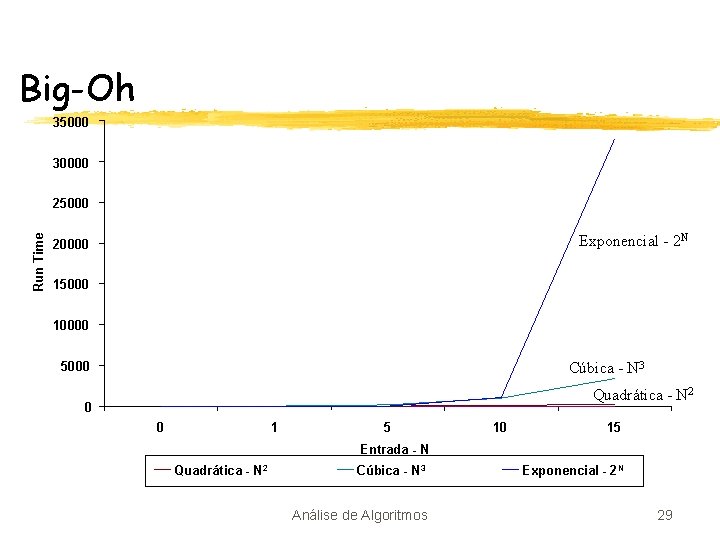
Big-Oh 35000 30000 Run Time 25000 Exponencial - 2 N 20000 15000 10000 Cúbica - N 3 5000 Quadrática - N 2 0 0 1 5 10 15 Entrada - N Quadrática - N 2 Cúbica - N 3 Análise de Algoritmos Exponencial - 2 N 29

Big-Oh Baseados nos gráficos, vemos que podemos classificar as funções em ordem crescente de tempo de execução ð Esta ordem pode ser dada por: ü ü ü ü Constante Logarítmica Log-quadrada Linear N log N Quadrática Cúbica Exponencial O(c) log N log 2 N N N log N N 2 N 3 2 N Análise de Algoritmos 30

Análise Assintótica de Algoritmos ð A análise assintótica de algoritmos descreve o tempo de execução em notação big-Oh ð Para realizar a análise assintótica: ü Calculamos o número de operações primitivas executadas como função do tamanho da entrada. ü Expressamos esta função na notação big-Oh ð Exemplo: ü Determinamos que o algoritmo array. Max executa no máximo 4 n 1 operações primitivas ü Logo, dizemos que o algoritmo array. Max “executa em tempo O(n)” Análise de Algoritmos 31

Análise Assintótica de Algoritmos ð Com a notação Big-Oh nós só estamos preocupados com o termo dominante. Por exemplo: ü Quadrática - provavelmente é C 1 N 2 + C 2 N + C 3 ü Cúbica - provavelmente é C 1 N 3 + C 2 N 2 + C 3 N + C 4 ð Novamente, nossa preocupação com os tempos só passa a ser relevante quando o n cresce muito e: lim n (n/n 2) = 0 (por L’Hôpital) Análise de Algoritmos 32

Análise Assintótica de Algoritmos ð É da aplicação de limites que tiramos os fundamentos teóricos para determinação de f(n) ser ou não g(n). ð Basicamente, podemos determinar que f(n) é O(g(n)) se e somente se: lim n (f(n)/g(n)) = c Note que alguns livros usam 0 ao invés de c mas isto faria com que f(n) não fosse da ordem de f(n), o que é um erro. Análise de Algoritmos 33

Limites inferiores ð A notação O fornece limites superiores para o crescimento de nossas funções, mas existem outras notações que podem fornecer mais informações interessantes sobre o crescimento do tempo de execução de nossos algoritmos. ð Seja (g(n)) o conjunto de funções f(n) para as quais existem constantes não negativas c e n 0 tais que: f(n) cg(n) n n 0 g(n) fornece um limite inferior para o crescimento de f(n) Análise de Algoritmos 34

Exemplos ð f(n) = 12 n 2 – 10 (1) ð f(n) = 12 n 2 – 10 (n 2) ð Entretanto f(n) = 12 n 2 – 10 (n 3) Análise de Algoritmos 35

Na prática … ð Para g(n) nós usamos a maior função que seja adequada Dizer que f(n) = 3 n 2 + 10 = (1) é correto, , mas não nos fornece muita informação sobre f(n)! ðPara g(n) nós usamos o termo de crescimento mais rápido em f(n) ðNós escrevemos f(n) = (g(n)) ao invés do mais correto f(n) (g(n)) Análise de Algoritmos 36

Quando os limites inferiores e superiores coincidem. . . ð Quando uma função pertence simultaneamente a O(g(n)) e a (g(n)) dizemos que f(n) (g(n)) f(n) = (g(n)) Mais precisamente, o conjunto (g(n)) é o conjunto de todas as funções para as quais existem constantes não negativas c 1, c 2, n 0 tais que: c 1 g(n) f(n) c 2 g(n) Análise de Algoritmos n n 0 37