Analytick vyjadrenie priamky v rovine Lenka Rotrov III

Analytické vyjadrenie priamky v rovine Lenka Roštárová III. F 2010/2011

ANALYTICKÁ GEOMETRIA je časť matematiky, v ktorej sú geometrické útvary vyjadrené pomocou čísel analytická geometria predstavuje prevedenie geometrických úloh na úlohy algebrické jej začiatky utvorili okolo roku 1635 francúzski matematici Piere de Fermat a René Descartes zaviedli súradnice bodov, ale nepoznali pojem vektor

Súradnicová sústava najčastejšie používaným súradným systémom je Karteziánska súradnicová sústava tiež ju voláme Euklidovsky dvojrozmerná súradnicová sústava označujeme ju E 2 pomocou KSS vieme každému bodu v rovine jednoznačne pridať usporiadanú dvojicu reálnych čísel túto dvojicu voláme súradnice daného bodu Súradnice bodov zapisujeme takto: A = [x, y], B = [a, b]. . .

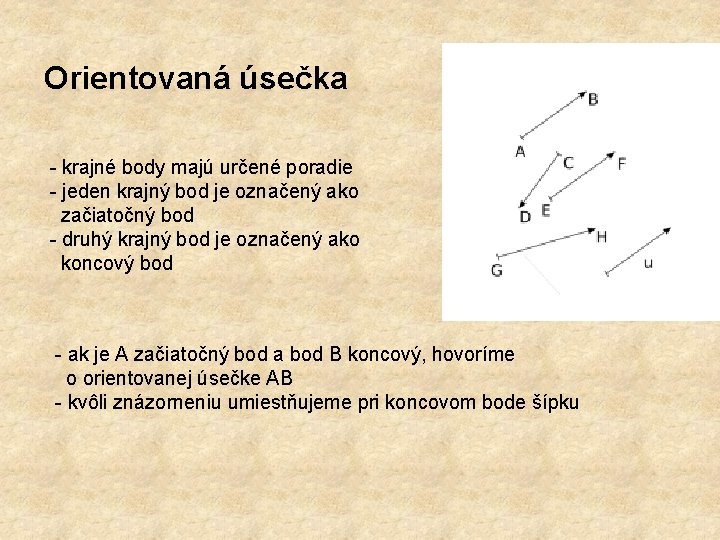
Orientovaná úsečka krajné body majú určené poradie jeden krajný bod je označený ako začiatočný bod druhý krajný bod je označený ako koncový bod ak je A začiatočný bod a bod B koncový, hovoríme o orientovanej úsečke AB kvôli znázorneniu umiestňujeme pri koncovom bode šípku

Vektory určený dĺžkou, smerom a orientáciou predstavujeme si ho ako orientovanú úsečku dve rôzne orientované úsečky, ktoré majú zhodnú dĺžku, smer aj orientáciu, predstavujú ten istý vektor nazývame aj množinou všetkých súhlasne orientovaných úsečiek s rovnakou dĺžkou označujeme malými písmenami a nad ne umiestňujeme šípku A[a 1, a 2] a bod B[b 1, b 2] AB = B – A = [b 1, b 2] – [a 1, a 2] = (b 1 a 1; b 2 a 2) = a Súradnice vektora zapisujeme takto: a (a, b), c (c 1, c 2). . .

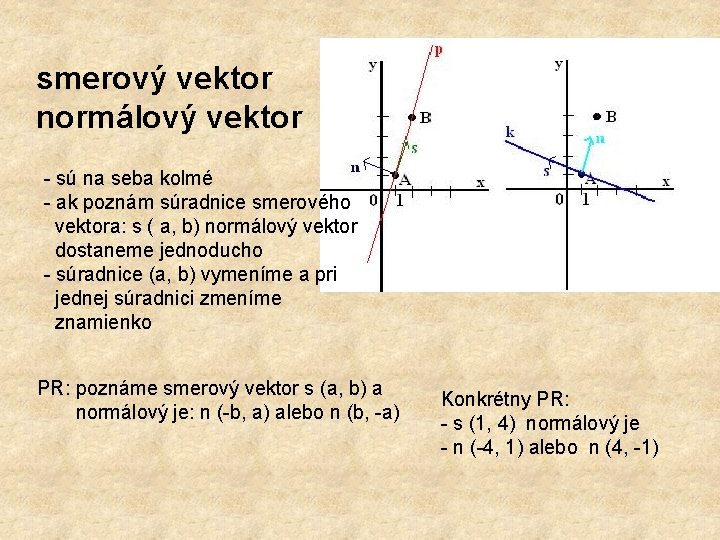
smerový vektor normálový vektor sú na seba kolmé ak poznám súradnice smerového vektora: s ( a, b) normálový vektor dostaneme jednoducho súradnice (a, b) vymeníme a pri jednej súradnici zmeníme znamienko PR: poznáme smerový vektor s (a, b) a normálový je: n ( b, a) alebo n (b, a) Konkrétny PR: s (1, 4) normálový je n ( 4, 1) alebo n (4, 1)

ROVNICE VYJADRUJÚCE PRIAMKU V ROVINE parametrická rovnica priamky v rovine všeobecná rovnica priamky v rovine smernicový tvar rovnice priamky v rovine úsekový tvar rovnice priamky v rovine

Parametrická rovnica priamky v rovine P[x 1, y 1] a bod Q[x 2, y 2], ktoré patria priamke p PQ = Q – P = [x 2, y 2] – [x 1, y 1] = (x 2 x 1; y 2 y 1)=s má nasledovný tvar p: x = x 1+ (x 2 x 1)t y = y 1+ (y 2 y 1)t Každá priamka sa dá parametricky vyjadriť!

Konkrétny príklad bod P[1, 2] a bod Q[3, 5], ktoré partia priamke p spravíme orientovanú úsečku PQ z orientovanej úsečky PQ vieme smerový vektor PQ = Q – P = [3, 5] – [1, 2] = (3 1; 5 2) = (2; 3) = s - Parametrická rovnica priamky v rovine má potom takýto tvar p 1: x = 1 + 2 t alebo( keď použijeme bod Q) p 2: x = 3 + 2 t y = 2 + 3 t y = 5 + 3 t Príklad 1: Napíšte parametrické vyjadrenie priamky p v rovine, ktorá prechádza bodmi A[6, 5], B[2, 8]. Riešenie: Poznáme body, ktoré patria priamke. Vypočítame si smerový vektor z vektora AB. AB = B – A = [2, 8] – [6, 5] = ( 4, 3) = s p: x = 6 – 4 t alebo p: x = 2 – 4 t y = 5 + 3 t y = 8 + 3 t

Príklad 2: Priamka je parametricky vyjadrená p: x = 4 + 7 t Vypočítajte bod, ktorým priamka y = 3 – 6 t. prechádza. Riešenie: Vieme, že bod Z[4, 3] patrí priamke p a smerový vektor tejto priamky je: s (7, 6). Potrebujem si dopočítať bod F, ktorého súradnice nepoznám. Postupujem ZF = F – Z = [x, y] – [4, 3] = (7, 6) (x – 4, y – 3) = (7, 6) x – 4 = 7 y – 3 = 6 x = 11 y = 3 F[11, -3] Príklad 3: Máme danú priamku p: x = 3 – t Napíšte param. vyjad. priamky q, tak aby q y = 2 + 3 t bola rovnobežná s priamkou p. Priamke q patrí bod Q[1, 10]. Riešenie: Z priamky p vieme, že smerový vektor je s( 1, 3). Aby boli priamky rovnobežné musia mať rovnaký smerový vektor. Keďže máme smerový vektor a poznáme aj súradnice bodu, ktorým priamka q prechádza, vieme jednoducho napísať parametrické vyjadrenie q. q: x = 1 – t y = 10 + 3 t

Všeobecná rovnica priamky v rovine získame vylúčením parametra z parametrického vyjadrenia Všeobecná rovnica priamky má potom tvar p: ax + by + c = 0 Konkrétny príklad A[1, 2] a bod B[5, 9] z dvoch bodov vieme vypočítať a vyjadriť všeobecnú rovnicu z bodov A, B vypočítame smerový vektor: AB = B – A = [5, 9] – [1, 2] = (4, 7) = s normálový vektor je: n 1 = ( 7, 4) alebo n 2 = (7, 4) dosadím do všeobecnej rovnici priamky: 7 x + 4 y + c = 0 dosadzujem bod A[1, 2] do rovnice: 7 x + 4 y + c = 0 7*1 + 4*2 + c = 0 7 + 8 + c = 0 c = 1 konečná všeobecná rovnica priamky v rovine je : -7 x + 4 y – 1 = 0

Príklad 1: Priamka p je určená bodmi C[2, 3], D[5, 1]. Urči jej všeobecnú rovnicu. Riešenie: vypočítame smerový vektor : CD = D – C = [5, 1] – [2, 3] = (3, 2) = s Zo smerového vypočítame normálový vektor: n = (2, 3) – dosadíme do tvaru všeobecnej rovnice: 2 x + 3 y + c = 0 Dosadíme súradnice bodu C[2, 3] : 2*2 + 3*3 + c = 0 4 + 9 + c = 0 c = 13 Koeficient c dosadíme do pôvodnej rovnice : 2 x + 3 y – 13 = 0 Príklad 2: Priamka p je určená param. vyjadrením p: x = 7 + 3 t Určte jej všeobecnú rovnicu. y = 5 – 2 t Riešenie: poznáme smerový vektor s = (3, 2). Z neho si vieme spraviť normálový vektor: n = (2, 3). Normálový vektor dosadíme: 2 x + 3 y + c = 0. Dosadíme si bod [7, 5] : 2*7 + 3*5 + c = 0 14 + 15 + c = 0 c = – 29 Dosadíme do rovnice: 2 x + 3 y – 29 = 0

Smernicový tvar rovnice priamky v rovine Smernicový tvar získame zo všeobecnej rovnice priamky p: ax + by + c = 0, ak b je rôzne od nuly, potom môžeme celú rovnicu deliť b čkom a po úprave dostanem : y = – a/b*x – c/b , kde k = – a/b , q = – c/b Smernicový tvar rovnice priamky p : y = kx + q Smernica k definovaná ako k = tg α Uhol α patrí uzavretému intervalu 0 až 180 stupňov α nemôže byť 90 stupňov, lebo vtedy by bola priamka rovnobežná s y osou a vtedy nevieme napísať smernicový tvar. Ale ak je priamka rovnobežná s osou x, tak vieme napísať smernicový tvar priamky.

Smernicu priamky vieme vypočítať aj iným spôsobom. Ak má priamka smerový vektor u = [u 1, u 2], kde u 1 je rôzne od nuly, tak má smernicu k = u 2/u 1. Ak u 1 = 0, potom priamka nemá smernica. Príklad 1: Určte smernicu a napíšte smernicový tvar rovnice priamky, ktorá je daná všeobecnou rovnicou 2 x – 3 y – 7 = 0. Riešenie: Ide len o algebrickú úpravu rovnice, lebo vieme, že smernicový tvar dostaneme zo všeobecného. Vyjadríme si jednoducho y: 2 x – 3 y – 7 = 0 3 y = 2 x – 7 y = 2/3*x – 7/3 Smernicový tvar je teda: y = 2/3*x – 7/3 a smernica je : k = 2/3

Príklad 2: Určte smernicu priamky, ktorá prechádza bodmi A [3, 5], B[2, 1]. Riešenie: Keďže poznáme súradnice ľahko si vyjadríme všeobecnú rovnicu priamky a to nasledovne: AB = B – A = [2, 1] – [3, 5] = ( 1, 4) = s. Zo smerového vieme normálový vektor: n = (4, 1). Napíšeme všeobecnú rovnicu: 4 x – y + c = 0 a dosadíme bod B[2, 1] 4*2 – 1 + c = 0 8 – 1 + c = 0 c = – 7 Všeobecná rovnica má tvar: 4 x – y – 7 = 0. Vyjadríme si smernicový tvar: y = 4 x – 7 a zo základného tvaru p : y = kx + q vieme, že k = 4. Alebo: Tento príklad sa dal vypočítať aj nasledovne: Máme smerový vektor s = ( 1, 4), kde 1 je rôzne od nuly (je splnená podmienka), tak smernica má potom tvar: k = u 2/u 1 k = 4/ 1 k = 4

Príklad 3: Napíšte všeobecnú rovnicu priamky, ktorá má smernicu k = 2 a prechádza bodom D[3, 1]. Riešenie: Pomocou smernicového tvaru y = kx + q vieme, že y = – 2 x + q. Z tohto tvaru si vieme vyjadriť všeobecný tvar: 2 x + y – q = 0. Dosadím si bod D[3, 1] 2*3 + 1 –q = 0 q = 7 Všeobecná rovnica potom vyzerá takto: 2 x + y + 7 = 0

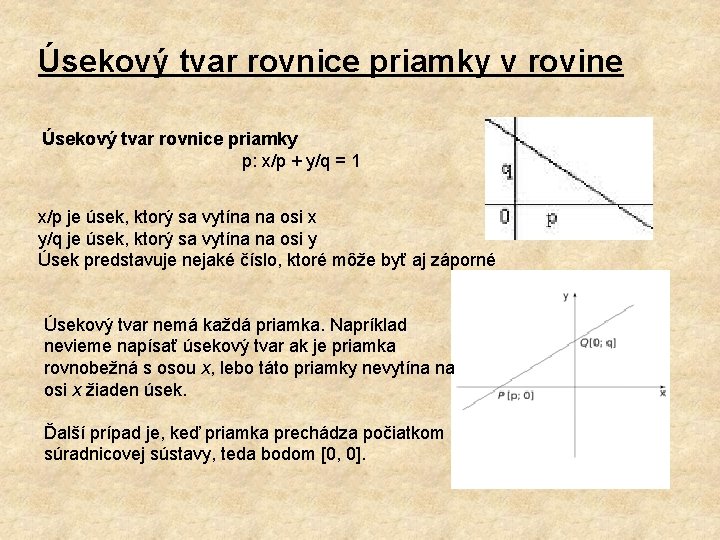
Úsekový tvar rovnice priamky v rovine Úsekový tvar rovnice priamky p: x/p + y/q = 1 x/p je úsek, ktorý sa vytína na osi x y/q je úsek, ktorý sa vytína na osi y Úsek predstavuje nejaké číslo, ktoré môže byť aj záporné Úsekový tvar nemá každá priamka. Napríklad nevieme napísať úsekový tvar ak je priamka rovnobežná s osou x, lebo táto priamky nevytína na osi x žiaden úsek. Ďalší prípad je, keď priamka prechádza počiatkom súradnicovej sústavy, teda bodom [0, 0].

Príklad 1: Všeobecnú rovnicu 3 x – y + 1 = 0 prepíšte na úsekový tvar. Riešenie: Vieme, že musíme dostať tvar: x/p + y/q = 1, preto si rovnicu jednoducho algebricky upravíme: 3 x – y + 1 = 0 3 x – y = 1 3 x + y = 1 – x/(1/3) + y/1 = 1 Príklad 2: Prepíšte úsekový tvar: x/ ( 1/3) + y/ ( 5/2) = 1 na všeobecný tvar rovnice. Riešenie: Rovnicu len upravujeme: x/ ( 1/3) + y/ ( 5/2) = 1 3 x – 2 y/5 – 1 = 0 /*5 15 x – 2 y – 5 = 0 15 x + 2 y + 5 = 0

ÚLOHA Priamka p je daná dvoma bodmi, A[2, 3] a B[ 2, 5]. Zostavte parametrickú a všeobecnú rovnicu, zapíšte priamku v smernicovom a úsekovom tvare , ak tieto tvary existujú. Riešenie: AB = B – A = [ 2, 5] – [2, 3] = (– 4, – 8) = s s = (– 4, – 8) n = (8, – 4) parametrická rovnica: x = 2 – 4 t y = 3 – 8 t všeobecná rovnica: 8 x – 4 y + c = 0 c = – 4 8*2 – 4*3 + c = 0 8 x – 4 y – 4 = 0 /: 4 16 – 12 + c = 0 2 x – y – 1 = 0 smernicový tvar: úsekový tvar: 2 x – y – 1 = 0 2 x – y = 1 y = 2 x – 1 x/ (1/2) + y/ 1 = 1

Pracovný list 1. Čo je úlohou analytickej geometrie? Jej úlohou je vyjadriť geometrické úlohy pomocou čísel. Predstavuje prevedenie geometrických útvarov na úlohy algebrické. 2. Ako sa volá najčastejšie používaný súradný systém? Uveďte aj druhé pomenovanie, ktoré sa používa. Karteziánsky súradný systém, nazývame ho aj Euklidovsky dvojrozmerný súradný systém. 3. Množina všetkých súhlasne orientovaných úsečiek s rovnakou dĺžkou je? vektor 4. V akom vzťahu je smerový vektor a normálový vektor? Smerový a normálový vektor sú vo vzťahu kolmosti = sú na seba kolmé.

5. Poznáme štyri rovnice na vyjadrenie priamky v rovine. Ktoré sú to ? parametrická rovnica priamky v rovine všeobecná rovnica priamky v rovine smernicový tvar rovnice priamky v rovine úsekový tvar rovnice priamky v rovine 7. Dá sa každá priamka parametricky vyjadriť? (správne zakrúžkuj!) áno – nie 8. Priamka p je daná bodom A[4, 2] a smerovým vektorom s = (2, 1). Zostavte jej parametrickú a všeobecnú rovnicu, zapíšte priamku v smernicovom a úsekovom tvare, pokiaľ tieto tvary existujú. parametrická rovnica smernicový tvar x = 4 + 2 t 2 y = – x + 8 /: 2 y = 2 – t y = –x/2 + 4 všeobecná rovnica úsekový tvar x + 2 y + c = 0 x + 2 y = 8 /: 8 4*1 + 2*2 + c = 0 x/8 + y/ 4 = 1 c = – 8 x + 2 y – 8 = 0

Ďakujem za pozornosť!