Priamka v rovine Analytick geometria linernych tvarov m

Priamka v rovine Analytická geometria lineárnych útvarov

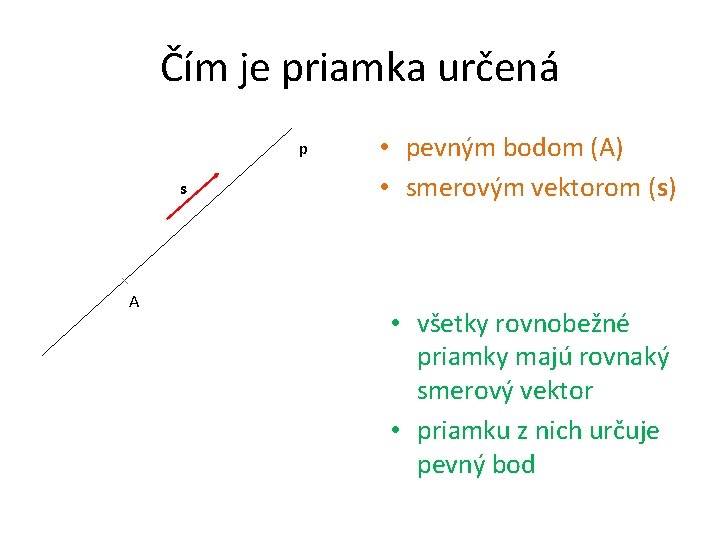
Čím je priamka určená p s A • pevným bodom (A) • smerovým vektorom (s) • všetky rovnobežné priamky majú rovnaký smerový vektor • priamku z nich určuje pevný bod

Ako priamku vyjadriť 1. Parametrickým vyjadrením (PVP) 2. Všeobecnou rovnicou (VRP) a) Základný tvar b) Smernicový tvar

Parametrické vyjadrenie priamky s p PVP: X = A + t. s, t R A[a 1; a 2] podľa súradníc: p: x = a 1 + t. s 1 y = a 2 + t. s 2 A s = (s 1; s 2)

Príklad 1 Napíšte PVP priamky, ktorá prechádza bodom A[1, -3] a má smerový vektor s = (2, -4) p: x = a 1 + t. s 1 y = a 2 + t. s 2 p: x = 1 + 2 t y = -3 – 4 t

Príklad 2 Napíšte PVP priamky, ktorá prechádza bodmi A[2, -4] a B[-3, -1] p: x = 2 – 5 t y = -4 + 3 t p: x = a 1 + t. s 1 y = a 2 + t. s 2 alebo p: x = -3 – 5 t y = -1 + 3 t

Príklady 1. Napíšte PVP priamky, ktorá prechádza bodom F[-2, 6] a má smerový vektor s = (-8, 9). 2. Napíšte PVP priamky, ktorá prechádza bodom H[5, -7] a má smerový vektor s = (0, 2). 3. Napíšte PVP priamky, ktorá prechádza bodmi S[-3, -3] a T[7, -6]. 4. Napíšte PVP priamky, ktorá prechádza bodmi E[0, 4] a F[4, 5]. riešenie

Príklady 5. Napíšte PVP priamky, ktorá prechádza bodom K[-3, -3] a je rovnobežná s priamkou p: x=1+3 t, y=4 -5 t. 6. Zistite, či body G[-2, 1], H[7, -6] ležia na priamke p: x=1+3 t, y=4 -5 t. 7. Napíšte PVP priamky, ktorá prechádza bodom E[0, 4] a je rovnobežná s priamkou, ktorá prechádza bodmi F[4, 5] a G[-3, -2]. riešenie

Príklady učebnica M 5 – riešené 49/Pr. 36 - 40 – neriešené 51/1 - 4

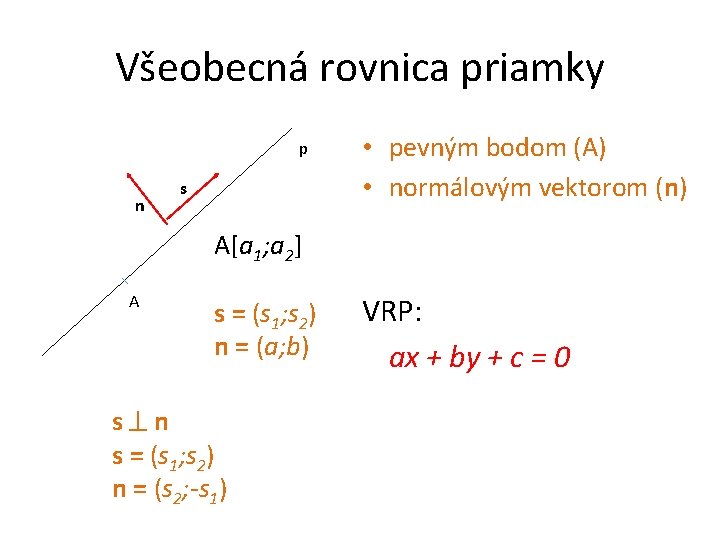
Všeobecná rovnica priamky p n s • pevným bodom (A) • normálovým vektorom (n) A[a 1; a 2] A s = (s 1; s 2) n = (a; b) s n s = (s 1; s 2) n = (s 2; -s 1) VRP: ax + by + c = 0

Príklad 3 Napíšte VRP priamky, ktorá prechádza bodom A[2, -4] a má normálový vektor n=(-3, -1) p: ax + by + c = 0

Príklad 4 Napíšte VRP priamky, ktorá prechádza bodmi A[2, -4] a B[-3, -1] p: ax + by + c = 0

Príklad 5 Napíšte PVP priamky, ktorá má rovnicu x – 2 y + 3 = 0 p: x = a 1 + t. s 1 y = a 2 + t. s 2 p: x = 1 + 2 t y= 2+t

Príklady 8. Napíšte VRP priamky, ktorá prechádza bodom F[-2, 6] a má normálový vektor n = (-8, 9). 9. Napíšte VRP priamky, ktorá prechádza bodom H[5, -7] a má smerový vektor s = (0, 2). 10. Napíšte VRP priamky, ktorá je kolmá na priamku, ktorá prechádza bodmi S[-3, -3] a T[7, -6]. 11. Napíšte VRP priamky, ktorá prechádza bodmi E[0, 4] a F[4, 5]. riešenie

Príklady 12. Nájdite bod a oba vektory priamky s vyjadrením p: x = 2 + 3 t, y = -3 – 5 t. 13. Napíšte VRP priamky, ktorá má vyjadrenie p: x = 4 t; y = 4 + 1 t. 14. Napíšte PVP priamky, ktorá má rovnicu p: 2 x -3 y+6=0 riešenie

Príklady učebnica M 5 – riešené 53/Pr. 41 - 44 – neriešené 55/1 - 6

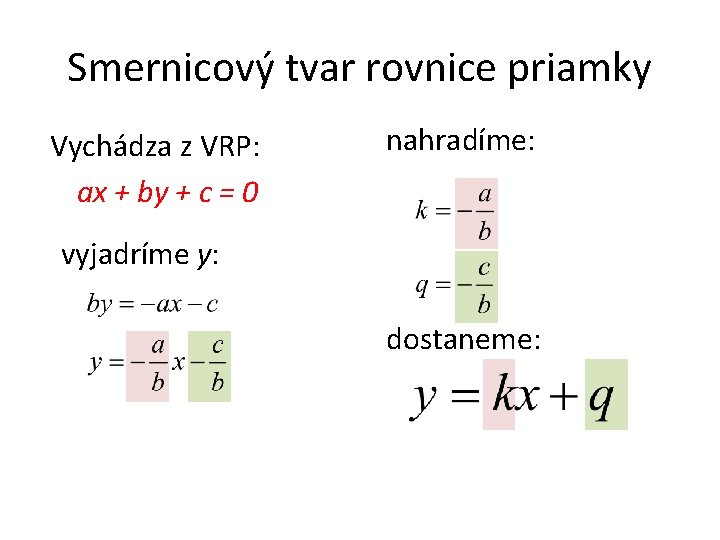
Smernicový tvar rovnice priamky Vychádza z VRP: ax + by + c = 0 nahradíme: vyjadríme y: dostaneme:

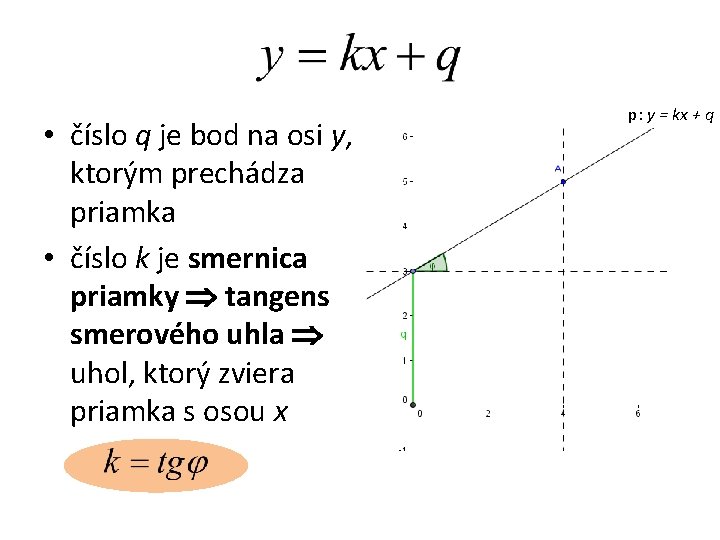
• číslo q je bod na osi y, ktorým prechádza priamka • číslo k je smernica priamky tangens smerového uhla uhol, ktorý zviera priamka s osou x p: y = kx + q

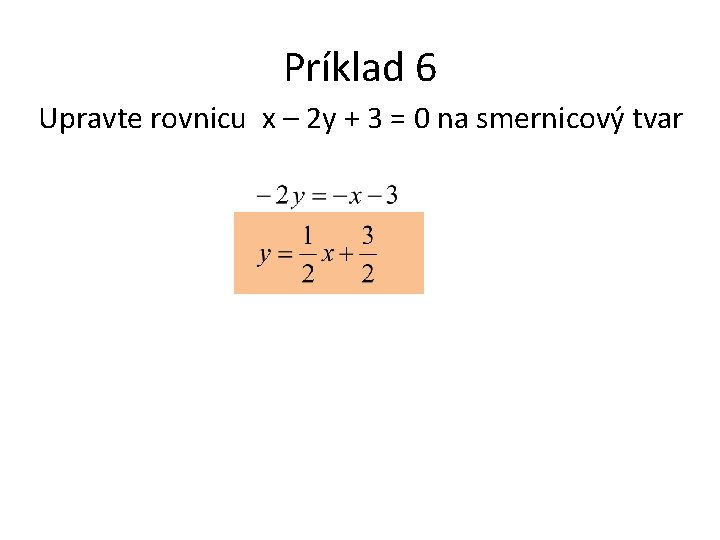
Príklad 6 Upravte rovnicu x – 2 y + 3 = 0 na smernicový tvar

Príklad 7 Napíšte smernicový tvar rovnice priamky a jej všeobecnú rovnicu, ak prechádza bodom A[-2, 3] a s osou x zviera uhol 45.

Príklady učebnica M 5 – riešené 56/Pr. 45, 58/Pr. 46 – 49 – neriešené 60/1 – 8

koniec

Riešenia 1. 2. 3. 4. 5. 6. 7. p: x = -2 – 8 t; y = 6 + 9 t p: x = 5; y = -7 + 2 t p: x = -3 + 10 t; y = -3 – 3 t p: x = 4 t; y = 4 + 1 t p: x = -3 + 3 t, y = -3 – 5 t bod G neleží, bod H leží p: x = – 7 t, y = 4 – 7 t

Riešenia 8. p: 8 x – 9 y + 70 = 0 9. 2 x – 10 = 0 10. 10 x – 3 y + 21 = 0 11. x – 4 y + 16 = 0 12. A[2; -3], s = (3; -5), n = (5; 3) alebo n = (-5; -3) 13. y – 4 = 0 14. napr: p: x = 3 t, y = 2+2 t späť