Analtisk eometrija Datorikas nodaas 2 kurss 1998 gada

Analītiskā ģeometrija Datorikas nodaļas 2. kurss 1998. gada rudenī 2. daļa. Figūras

Figūru vienādojumi: Priekšvārds Figūras analītiskajā ģeometrijā apraksta ar tajās ietilpstošo punktu koordinātēm. Punktu koordinātes var apmierināt kādu vienādojumu F(x, y)=0, šis vienādojums var būt atrisināts pret x vai y, vai arī abas koordinātes var būt izteiktas ar parametriem. Ģeometrisko figūru īpašības un attiecības aizstāj figūru vienādojumi un to attiecības. Vienādojumus var būt ērti pētīt ar algebriskām metodēm, jo tad nav jārūpējas par katra starprezultāta ģeometrisko jēgu. Pēc vienādojuma izskata izšķir 1. un 2. kārtas algebriskās līnijas un virsmas: taišņu un plakņu vienādojumiem ir 1. kārta, bet, piemēram, elipses, parabolas un hiperbolas vienādojumiem ir 2. kārta. Šīs figūras jāpēta nevis tādēļ, ka tās ir “vajadzīgākās”, bet tādēļ, ka citas ar tik vienkāršām metodēm nevar izpētīt: Pazudušais naudasmaks jāmeklē tur, kur ir gaišāks.

Taisnes parametriskais v-ms Problēma: Aprakstīt taisni, kas iet caur punktu vektora virzienā. Izvēlamies kādu citu punktu M’ uz taisnes. Vektors ir kolineārs tātad kādam Punkta Tad , rādiusvektoru apzīmējam ar - taisnes parametriskais vienādojums. Koordinātu formā:

Taisnes kanoniskais v-ms Izslēdzam parametru Iegūstam: no taisnes parametriskā vienādojuma. Taisnes 3 D kanoniskais vienādojums. Taisnes 2 D kanoniskais vienādojums. Piezīme: Ja, piemēram, (taisne paralēla prasām, lai kanoniskajā vienādojumā. Analoģiski, ja vai. plaknei ),

Taisne caur 2 punktiem Problēma: Doti divi punkti kas iet caur tiem. Reducējam problēmu uz parametrisko vienādojumu ar virziena vektoru O Kanoniskajā formā kur un

2 D taisne ar determinantu Kanoniskais vienādojums 2 D taisnei, kas iet caur punktiem un : Izvairāmies no speciālgadījumiem Pārrakstām kā determinantu: vai :

Taisnes vienādojums un trijstūra laukums Determinants reizinājumu kur izsaka pseidoskalāro , , , Trijstūra S Nav brīnums, ka determinants ir. . laukums ir (ar pretēju zīmi, ja doti pulksteņa rādītāju kustības virzienā). atrodas uz taisnes tikai tad, ja

2 D Taisnes vispārīgais vienādojums Savelkot locekļus, kas satur un vienādojumā , iegūstam Apzīmējam , , Taisnes virziena vektors ir ortogonāli pārbaude ar skalāro reizinājumu, un vektors

2 D taisnes normālais v-ms Problēma: Dots vektors un skaitlis ; aprakstīt taisni, kas perpendikulāra normāles vektoram un atrodas attālumā no koordinātu sākumpunkta Izvēlamies punktu uz taisnes. Tā rādiusvektora r proekcija uz vektora ir. Tātad - taisnes normālais vienādojums. Koordinātu formā:

Taisnes vispārīgais un normālais v-mi Vispārīgais vienādojums atgādina normālo: tikai ir papildprasība: , Vispārīgo vienādojumu izdalot ar , t. i. vektora garumu, tas kļūst par normālo: jeb Arī , kur ir taisnes normāles vektors, tikai nav nonormēts.

Taisnes v-ms asu nogriežņos Problēma: Dota taisne, kas nav paralēla nevienai no koordinātu asīm, neiet caur sākumpunktu; atrast tās vispārīgo vienādojumu pēc grafika vai grafiku pēc vispārīgā vienādojuma. Ja taisne uz asīm un atšķeļ nogriežņus un , tad tās vienādojums ir: (to apmierina punkti un tādeļ arī citi punkti uz taisnes) Otrādi: taisne ar vienādojumu atšķeļ uz asīm nogriežņus un ,

Plaknes parametriskais v-ms Problēma: Aprakstīt plakni, kas iet caur punktu paralēla vektoriem un ir un Izvēlamies kādu citu punktu šajā plaknē. Tad izsakās ar un : Tādēļ . rādiusvektors Tas ir plaknes parametriskais vienādojums ar diviem parametriem

Plakne caur 3 punktiem Problēma: Aprakstīt plakni, kas iet caur punktiem Problēmu var pārrakstīt kā parametrisko vienādojumu virzienu vektoriem un

Plakne caur 3 punktiem ar determinantu Lai punkts un atrastos vienā plaknē ar vajag lai vektori būtu komplanāri, t. i. jauktais reizinājums Vispārīgā gadījumā šis deteminants ir seškārtīgs tetraedra tilpums (ar + vai - zīmi atkarībā no vektoru orientācijas).

Plaknes vispārīgais vienādojums Savelkot determinanta izteiksmē koeficientus pie iegūsim plaknes vispārīgais vienādojums. Vektors ir perpindikulārs plaknes virziena vektoriem un , tādēļ tas perpendikulārs pašai plaknei.

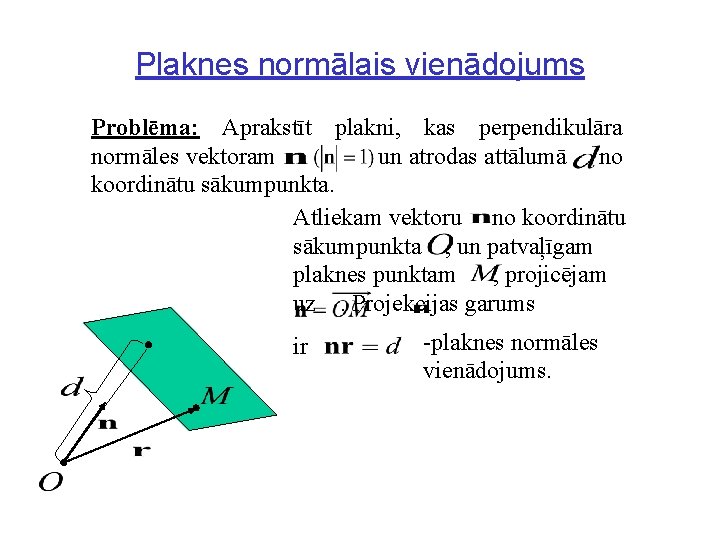
Plaknes normālais vienādojums Problēma: Aprakstīt plakni, kas perpendikulāra normāles vektoram un atrodas attālumā no koordinātu sākumpunkta. Atliekam vektoru no koordinātu sākumpunkta , un patvaļīgam plaknes punktam , projicējam uz. Projekcijas garums ir -plaknes normāles vienādojums.

Plaknes vispārīgais un normālais v-mi Vispārīgajā vienādojumā vektors arī ir normāles vektors, tikai nav normēts. Pārrakstām vispārīgo vienādojumu: , kur . Izdalām abas puses ar Iegūstam Tas ir normālais vienādojums, ja apzīmē un .

Plaknes v-ms asu nogriežņos Problēma: Aprakstīt plakni, kas nav paralēla koordinātu asīm un neiet caur koordinātu sākumpunktu, ja dots tās grafiks. Otrādi: atrast grafiku no vispārīgā vienādojuma. Ja plakne iet caur punktiem tad tās vienādojums ir Otrādi: ja dots vispārīgais plaknes vienādojums: , to pārraksta , kur ir nogriežņi, ko plakne atšķeļ uz asīm.

Taisnes uzdošana ar divām plaknēm Ja un nav kolineāri, tad abas plaknes ar šiem normāles vektoriem nav paralēlas, t. i. tās krustojas pa taisni. Šīs taisnes vektors ir perpendikulārs gan , gan tādēļ var izvēlēties Ja, piemēram, tad var atrisināt sistēmu tādejādi atrodot punktu Gadījumi vai uz taisnes ir analoģiski. .

Elipses jēdziens D Elipse ir figūra, ko kādā ortonormētā koordinātu sistēmā apraksta vienādojums Elipses kanoniskais vienādojums sauc par elipses pusasīm; izvēlamies Ja pieder elipsei, tad arī , un pieder elipsei. Tādēļ elipse ir simetriska pret abām asīm un koordinātu sākumpunktu

Elipses fokālā īpašība - I Elipsei apzīmējam – fokusu pusattālums. Punktus fokusiem. Ja un sauc par elipses (elipse ir rinķis), abi fokusi sakrīt. T (Elipses fokālā īpašība) Punkts pieder elipsei tad un tikai tad, ja

Elipses fokālā īpašība - II Pierādīsim, ka elipses punktam un Tā, kā elipses punktiem. Izteiksmi izpildās . Iegūstam un , tad pierāda analoģiski.

Elipses direktoriālā īpašība - II D Skaitli Elipsei D Taisnes sauc par elipses ekscentritāti. , riņķa līnijai un . sauc par elipses direktrisēm. Riņķa līnijai tās nav definētas. T (Elipses direktoriālā īpašība) Katram elipses punktam attālumu attiecība līdz fokusam un atbilstošajai direktrisei vienāda ar.

Elipses direktoriālā īpašība - II Aplūkosim fokusu un atbilstošo direktrisi ar vienādojumu Kā redzējām iepriekš, patvaļīgam punktam uz elipses Attālums no M līdz vertikālajai taisnei ir Iegūstam Otram fokusam un direktrisei pierādījums ir analoģisks.

Elipses optiskā īpašība T Patvaļīgā elipses punktā vilkta pieskare veido vienādus leņķus ar nogriežņiem un kas to savieno ar elipses fokusiem. Ja elipses iekšējā virsma atstaro gaismu un vienā fokusā ir gaismas avots, tad visi stari fokusējas otrā fokusā.

Parabolas kanoniskais v-ms D Parabola ir figūra, ko kādā ortonormētā koordinātu sistēmā apraksta vienādojums: (parabolas kanoniskais vienādojums) sauc parabolas parametru. Ja pieder parabolai, tad arī pieder parabolai. Tādēļ parabola ir simetriska pret abscisu asi.

Parabolas direktoriālā īpašība - I D Parabolai fokusu, bet taisni punktu sauc par direktrisi. T (Parabolas direktoriālā īpašība). Katram parabolas punktam tā attālumi līdz fokusam un direktrisei ir vienādi (t. i. , to attiecîba ir 1, ko var uzskatît parabolas ekscentritāti).

Parabolas direktoriālā īpašība - II Pierādīsim, ka patvalīgam parabolās punktam izpildas Tā kā visiem parabolas punkiem Viegli redzēt, ka arī attālums no līdz vertikālai taisnei ir , tad

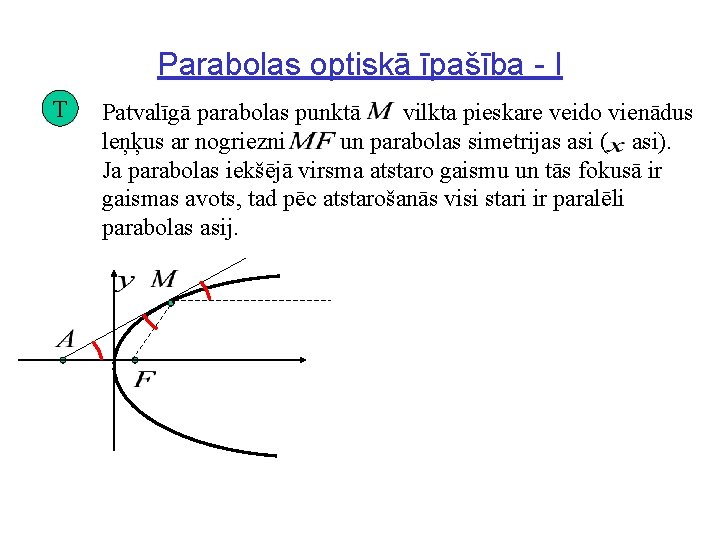
Parabolas optiskā īpašība - I T Patvalīgā parabolas punktā vilkta pieskare veido vienādus leņķus ar nogriezni un parabolas simetrijas asi ( asi). Ja parabolas iekšējā virsma atstaro gaismu un tās fokusā ir gaismas avots, tad pēc atstarošanās visi stari ir paralēli parabolas asij.

Parabolas optiskā īpašība - II Funkcijai punktā vilktajai pieskarei ir vienādojums Ja parabolas punkts atrodas virs funkcijas vienādojums ass, tad un atvasinājums Tātad pieskares vienādojums ir jeb , jeb Pieskare krusto asi punktā. Attālums no turienes līdz fokusam ir t. i. tāds pat kā. Tātad ir vienādsānu trijstūris.

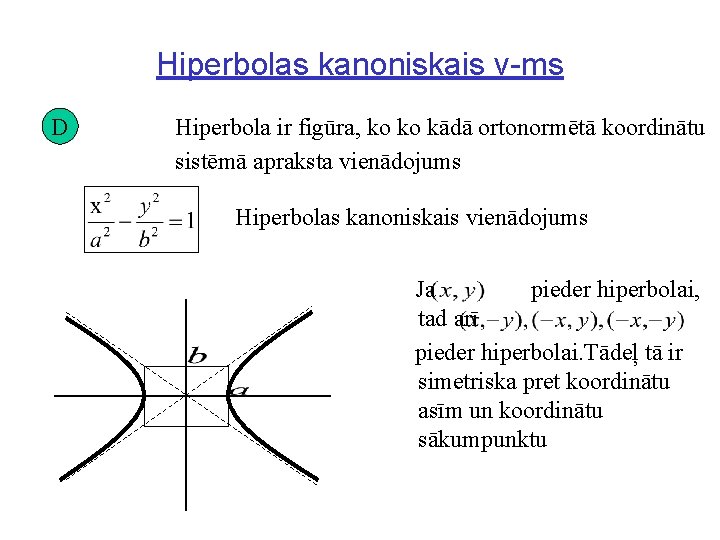
Hiperbolas kanoniskais v-ms D Hiperbola ir figūra, ko ko kādā ortonormētā koordinātu sistēmā apraksta vienādojums Hiperbolas kanoniskais vienādojums Ja pieder hiperbolai, tad arī pieder hiperbolai. Tādeļ tā ir simetriska pret koordinātu asīm un koordinātu sākumpunktu

Hiperbolas fokālā īpašība - I Hiperbolai apzīmējam - fokusu pusattālums Punktus un sauc par hiperbolas fokusiem. T (Hiperbolas fokālā īpašība) Punkts pieder hiperbolai tad un tikai tad, ja Izteiksmei ir dažādas zīmes uz dažādiem hiperbolas zariem.

Hiperbolas fokālā īpašība - II Pierādīsim, ka hiperbolas punktam un attālums , kur “+” zīme ir labajam hiperbolas zaram, bet “-” zīme - kreisajam. Izteiksme modulī ir pozitīva labajam zaram un negtīva krejsajam. izteiksmi pierāda analoģiski.

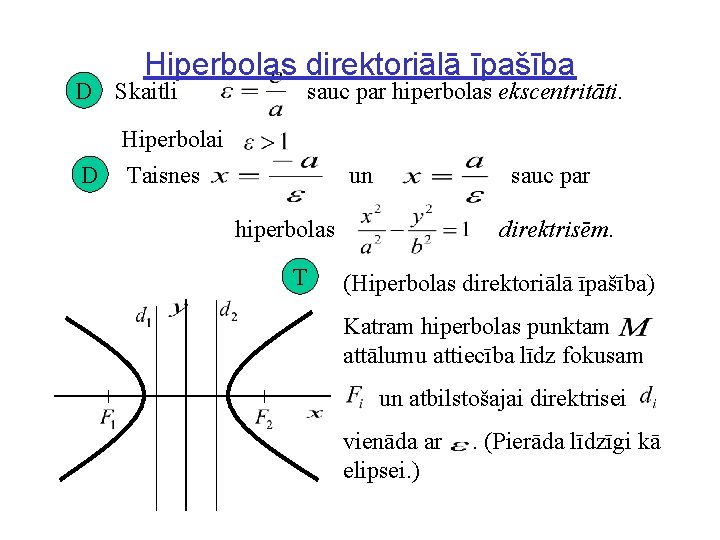
Hiperbolas direktoriālā īpašība D Skaitli sauc par hiperbolas ekscentritāti. Hiperbolai D Taisnes un sauc par hiperbolas T direktrisēm. (Hiperbolas direktoriālā īpašība) Katram hiperbolas punktam attālumu attiecība līdz fokusam un atbilstošajai direktrisei vienāda ar elipsei. ) . (Pierāda līdzīgi kā

Hiperbolas optiskā īpašība T Patvaļīgā hiperbolas punktā M vilkta pieskare veido vienādus leņķus ar nogriežņiem, kas to savieno ar elipses fokusiem. (Bez pierādījuma. ) Ja kāda hiperbolas zara iekšējā virsma atstaro gaismu un atbilstošajā fokusā ir gaismas avots, tad pēc atstarošanas izskatās, ka gaisma nāk no otra fokusa.

Vienādsānu hiperbola Ja , tad hiperbolu sauc par vienādsānu hiperbolu. No koordinātēm pārejam uz citām koordinātēm ar pagriezienu par Tad vienādojumu Tātad var pārrakstīt sekojoši: t. i. hiperbola ir apgrieztās proporcionalitātes grafiks. :

Riņķa līnijas parametrizācija Punktu M(x, y) uz vienības riņķa līnijas x 2 + y 2 = 1 var izteikt ar trigonometriskajām funkcijām no leņķa , ko OM veido ar x asi. Apzīmējam: Tad Universālā trigometriskā substitūcija

Riņķa racionālā parametrizācija , pie kam Šī parametrizācija neapraksta punktu L(-1, 0), kas arī atrodas uz riņķa līnijas, jo tam nav definēts. Katram citam punktam M(x, y) uz vienības riņķa, parametrs t ir puse no KM , kur M ir taisnes LM un x = 1 krustpunkts.

Pitagora trijnieki - I D Ir Pitagora trijnieks, ja skaitļi, un. Punkts ir vesali atrodas uz vienības riņķa līnijas , jo Punktam jo atbilst racionāla parametra un un ir racionāli. vērtība,

Pitagora trijnieki - II Ja , kur Tātad varam izvēlēties un ir vesali skaitļi, tad

Fermā teorēma T Vienādojumam veselos skaitļos, ja (Bez pierādījuma). Vienādojumam daudz atrisinājumu: nav atrisinājumu ir naturāls un Piemēram, kad (t. i. toties ir bezgalīgi iegūstam atrisinājumu (3, 4, 5). Kad , iegūstam (5, 12, 13). un ),

Hiperboliskās funkcijas Aplūkojam vienādsānu hiperbolu Punkts atrodas uz hiperbolas. Apzīmējam laukumu, ko ierobežo ass, un hiperbolas zars ar. . T Katram hiperbolas punktam ir spēkā sakarības: (hiperboliskais kosinuss) kur (hiperboliskais sinuss) Viegli pārliecināties, ka katram ir spēkā

Vienādsānu hiperbolas parametrizācija Aplūkojam funkciju un ieviešam parametru . Tad , kur Šī sistēma apraksta visus punktus uz hiperbolas labā zara.