ANALISI E INTERPRETAZIONE DATI ANALISI DEI DATI SE

ANALISI E INTERPRETAZIONE DATI

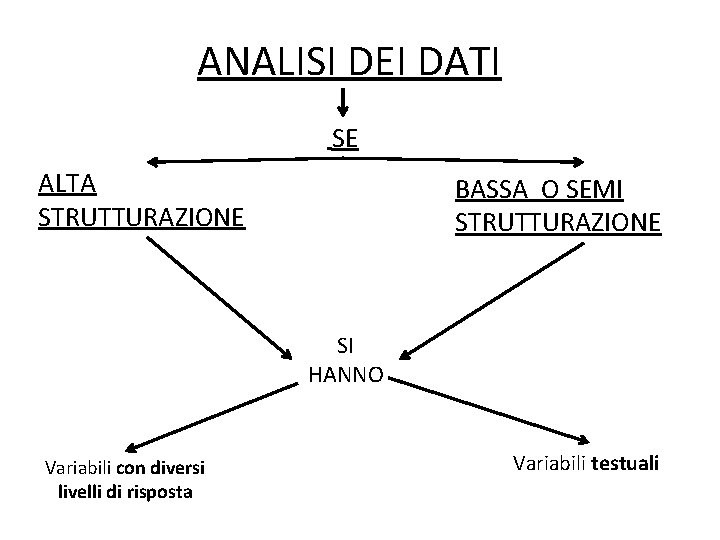
ANALISI DEI DATI SE ALTA STRUTTURAZIONE BASSA O SEMI STRUTTURAZIONE SI HANNO Variabili con diversi livelli di risposta Variabili testuali

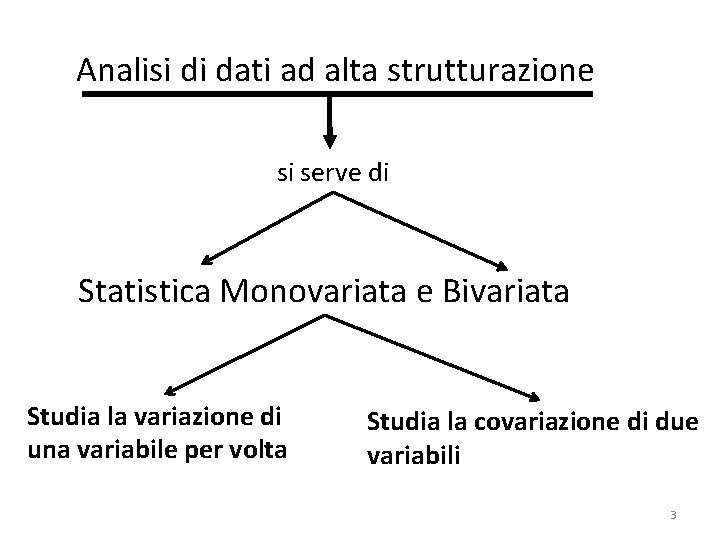
Analisi di dati ad alta strutturazione si serve di Statistica Monovariata e Bivariata Studia la variazione di una variabile per volta Studia la covariazione di due variabili 3

La statistica monovariata Può essere: Descrittiva descrive una data realtà educativa attraverso dei parametri quantitativi che ricavo dal campione Inferenziale inferisce parametri della popolazione a partire da quelli quantitativi del campione. 4 Nella statistica monovariata viene utilizzata la distribuzione di frequenza cioè come si distribuiscono i casi del campione nelle categorie delle variabili 4

SEMPLICE La distribuzione di frequenza CUMULATA Risposte possibili QUAL E’ IL VOSTRO TITOLO DI STUDIO? frequenze SEMPLICE frequenze CUMULATE (n 1; n 2; n 3. . ) Ni=n 1+n 2+…+ni elementari 30 30 medie 50 30+50=80 diploma 80 30+50+80=160 laurea 40 30+50+80+40=200

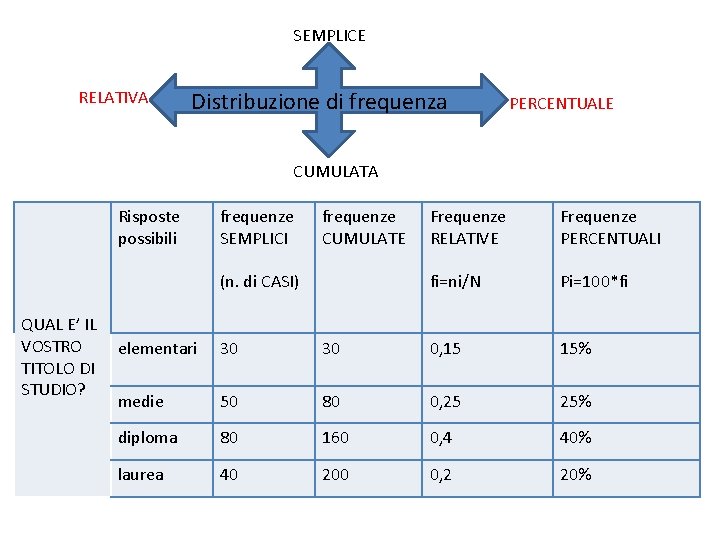
SEMPLICE RELATIVA Distribuzione di frequenza PERCENTUALE CUMULATA Risposte possibili frequenze SEMPLICI frequenze CUMULATE (n. di CASI) QUAL E’ IL VOSTRO TITOLO DI STUDIO? Frequenze RELATIVE Frequenze PERCENTUALI fi=ni/N Pi=100*fi elementari 30 30 0, 15 15% medie 50 80 0, 25 25% diploma 80 160 0, 4 40% laurea 40 200 0, 2 20%

Per vedere come si distribuiscono, complessivamente, i casi nei valori che la variabile può assumere utilizziamo gli indici di tendenza centrale e gli indici di dispersione. Ci permettono di misurare quanto e come si disperdono i dati. Sono: • SQUILIBRIO • CAMPO DI VARIAZIONE • DIFFERENZA INTERQUARTILICA • VARIANZA e DEVIAZIONE STANDARD Servono a stabilire come e dove si addensano i dati a nostra disposizione. Sono: • MEDIA • MODA • MEDIANA

Indici di tendenza centrale

MEDIA • È la somma dei valori assunti da tutti i casi diviso per il numero dei casi. Ha significato quando il numero dei casi è piuttosto alto. TOTALE CASI ESAMI SOSTENUTI 1 8 1 7 1 10 1 15 1 13 5 ES 1. 8, 7, 10, 15, 13 (esami sostenuti da cinque ragazzi) 8+7+10+15+13= 53 Media= 53(somma dei valori)/5 (numero dei casi) = 10, 6 media degli esami sostenuti

MEDIA ES 2. TOTALE CASI ESAMI SOSTENUTI 1 8 4 7 2 10 6 15 1 13 14 MEDIA= Totale esami sostenuti /Totale N. dei casi Media ES 2: [(8*1)+(7*4)+(10*2)+(15*6)+(13*1) ]/ 14= (8+28+20+90+13)/14 = 159/14= 11, 35

MODA • è la categoria con la frequenza più alta (nella quale si addensa il numero maggiore di casi), non in senso assoluto, ma relativo (non è necessario cioè che contenga il 50% dei casi, è sufficiente che sia quella con il numero maggiore di casi rispetto alle altre). ES 1. 8, 7, 10, 15, 13 In questo caso la MODA non esiste ES 2. 3, 7, 8, 7, 15, 13 7 è la moda perché è il valore che ricorre più volte N. DI CASI VALORI 1 3 2 7 1 8 1 13 1 15

MEDIANA • è il punto centrale delle distribuzione ordinata e divide il campione in due parti. CASI ES 1. 8, 7, 10, 15, 13 La serie deve essere disposta in ordine crescente 7, 8, 10, 13, 15 M=10 TOTA LE ES 2. 7, 8, 10, 13 M = 4 /2 = 2 La Mediana si posiziona tra la seconda e la terza riga (seconda posizione rispetto alla frequenza cumulata), corrispondente a 9 ((10+8)/2 = 9) TOTALE ESAMI SOSTENUTI 1 1 7 1 2 8 1 3 10 1 4 13 1 5 15 5 CASI Freq. cumulata ESAMI SOSTENUTI 1 1 7 1 2 8 1 3 10 1 4 13 4

MEDIANA ES 3. TOTALE CASI Freq. cumulata ESAMI SOSTENUTI 2 2 7 1 3 8 3 6 13 2 8 15 8 M= 8/ 2= 4 La Mediana si posiziona nella terza riga (quarta posizione rispetto alla frequenza cumulata), in corrispondenza del 13 ((13+13) /2 = 13)

ATTENZIONE!!! La MODA Vale solo per variabili cardinali e categoriali e non è utilizzabile per i dati a bassa strutturazione. La MEDIANA Può essere applicata alle variabili cardinali ed alle variabili ordinate.

Indici di dispersione

LO SQUILIBRIO 1/2 • È la somma delle proporzioni al quadrato per ciascuna modalità della variabile. ES 1. ES. Pi=(30/90)* 100 ES. Pi=(33, 3/100) N. Di studenti (casi) Voto Percentuale Trasformazioni in proporzioni rispetto all’unità Quadrato delle proporzioni 30 21 33, 3% 0, 33² 0, 1089 5 25 5, 5% 0, 05² 0, 0025 35 27 38. 8% 0, 39² 0, 1521 5 29 5, 5% 0, 05² 0, 0025 15 30 16, 6% 0, 17² 0, 0289 TOT: 90 ~100%

LO SQUILIBRIO 2/2 ES 1. Quadrato delle proporzioni 0, 1089 0, 0025 0, 1521 SQUILIBRIO= 0, 1089+0, 0025 +0, 1521+0, 0025+0, 0289= 0, 0025 0, 0289 0. 2949 • La somma dei quadrati delle proporzioni è lo squilibrio e in questo caso è 0, 2949. • Il massimo squilibrio possibile è 1 mentre il minimo squilibrio è 1/k, dove k è la categoria. • Il minimo squilibrio lo abbiamo quando tutte le categorie hanno la stessa frequenza.

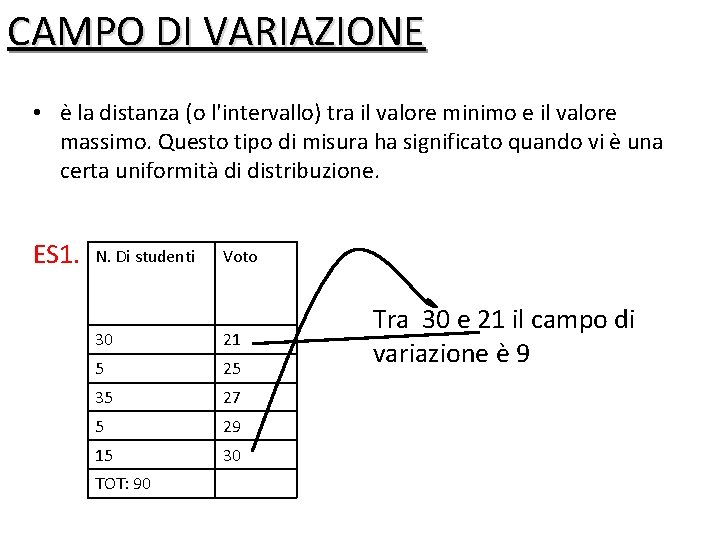
CAMPO DI VARIAZIONE • è la distanza (o l'intervallo) tra il valore minimo e il valore massimo. Questo tipo di misura ha significato quando vi è una certa uniformità di distribuzione. ES 1. N. Di studenti Voto 30 21 5 25 35 27 5 29 15 30 TOT: 90 Tra 30 e 21 il campo di variazione è 9

DIFFERENZA INTERQUARTILICA 1/2 • i quartili sono misure di posizione con cui dividiamo la nostra distribuzione in parti uguali pari al 25% del totale (si definisce in percentuale: 25%). I quartili dividono la popolazione in quattro parti: 25%, 50%, 75% e 100%. La differenza interquartilica è la distanza del valore posizionato sul 75% della distribuzione dal valore posizionato sul 25% della distribuzione. Consente di escludere i valori che si posizionano agli estremi della distribuzione di frequenza che possono essere significativamente differenti dal resto della distribuzione, perciò risulta spesso più efficace del campo di variazione.

DIFFERENZA INTERQUARTILICA 2/2 ES 1. N. Di studenti Voto Percentuale 30 21 33, 3% 5 25 5, 5% 38, 8% 35 27 38. 8% 77, 6% 5 29 5, 5% 83, 1% 15 30 16, 6% 99, 7% TOT: 90 Percentuale cumulata 33, 3+ 5, 5 =PC 33, 3% primo quartile Terzo quartile ~100% Distanza tra valore posizionato sul 75% della distribuzione e valore posizionato sul 25%. Quindi la differenza tra 27 e 21 è 6

DEVIAZIONE STANDARD 1/2 • è la radice della somma delle differenze di ciascun valore rispetto alla media elevato al quadrato e rapportato al numero di casi. Questo indice è in grado di indicare lo scostamento medio dei soggetti dalla media, ovvero il grado di eterogeneità o omogeneità delle risposte (quanto, mediamente, i punteggi/valori si discostano dalla media complessiva). Viene chiamata varianza quando non viene riportata sotto radice. ES 1. N. Di studenti Voto 30 21 5 25 35 27 5 29 15 30 TOT: 90 MEDIA= [ (21*30)+(25*5)+(27*35)+(29*5)+(30*15) ]/ 90= (630+125+945+145+450) /90= 2295/90= 25, 5

DEVIAZIONE STANDARD 2/2 ES 1. N. Di studenti Voto 30 21 5 25 35 27 5 29 15 30 MEDIA=25, 5 VARIANZA • è uguale alla deviazione standard, senza la radice TOT: 90 ∂= √{ [(21 - 25, 5)² *30] + [(25 - 25, 5)²*5] + [(27 - 25, 5)² *35]+ [(29 - 25, 5)² *5 ]+ [(30 - 25, 5)² *15 ] /90 }= √ [(20, 25*30) + ( 0, 25* 5) + (2, 25*35)+ (12, 25*5)+(20, 25*15)/ 90]= √ [(607, 5+1, 25+ 78, 75+ 61, 25+ 303, 75)/ 90 ] = √ (1052, 5/90) = √ 11, 69= 3, 42

ATTENZIONE!!! Lo SQUILIBRIO Vale solo per variabili cardinali e categoriali. Il CAMPO DI VARIAZIONE Vale solo per le variabili categoriali, cardinali e ordinate. La DIFFERENZA INTERQUARTILICA E’ possibile solo per le variabili categoriali ordinate e cardinali La DEVIAZIONE STANDARD Vale solo per le variabili cardinali

La statistica bivariata Individua la relazione tra due variabili. Una volta individuata la presenza di una relazione occorre precisarne la natura e quindi: Per verificare se una relazione tra variabili è significativa si può utilizzare il test del Chi quadro (χ2) • che direzione assume la relazione; • se si tratta di relazione positiva (ovvero se al crescere di x cresce anche y); • se si tratti, invece, di relazione negativa (opposta alla precedente); • se si tratta di relazione simmetrica o asimmetrica; • l'intensità e la forza della relazione che viene misurata attraverso specifici indici che misurano come si combina e con quale forza la variazione dei fenomeni che stiamo 24 esaminando.

CHI QUADRO • è dato dalla somma delle frequenze osservate nella realtà alle quali vengono sottratte le frequenze teoriche al quadrato e rapportate alle frequenze teoriche. Le frequenze teoriche si ottengono con i totali marginali di riga e di colonna. Per calcolarle si effettua una moltiplicazione e una divisione per ogni cella: si moltiplicano i due totali marginali corrispondenti e si divide per N (numero totale dei casi).

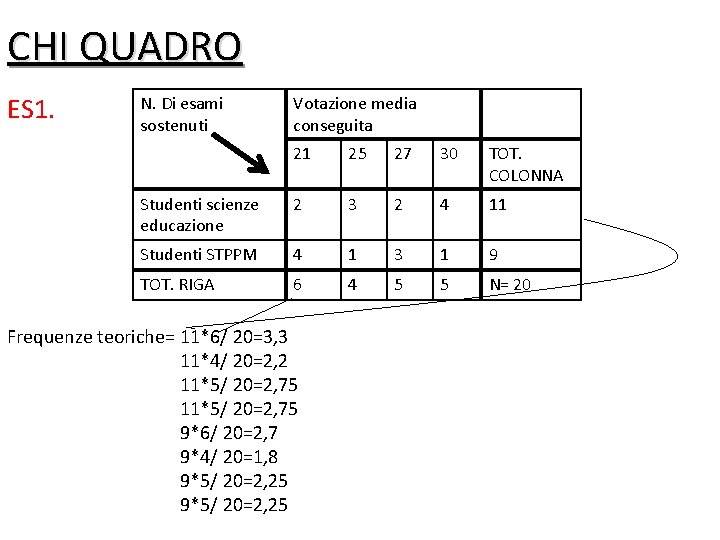
CHI QUADRO ES 1. N. Di esami sostenuti Votazione media conseguita 21 25 27 30 TOT. COLONNA Studenti scienze educazione 2 3 2 4 11 Studenti STPPM 4 1 3 1 9 TOT. RIGA 6 4 5 5 N= 20 Frequenze teoriche= 11*6/ 20=3, 3 11*4/ 20=2, 2 11*5/ 20=2, 75 9*6/ 20=2, 7 9*4/ 20=1, 8 9*5/ 20=2, 25

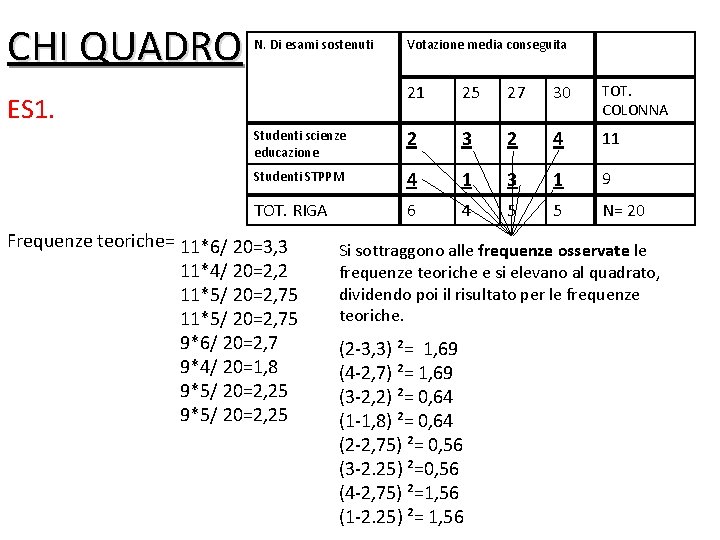
CHI QUADRO N. Di esami sostenuti Votazione media conseguita 21 25 27 30 TOT. COLONNA Studenti scienze educazione 2 3 2 4 11 Studenti STPPM 4 1 3 1 9 TOT. RIGA 6 4 5 5 N= 20 ES 1. Frequenze teoriche= 11*6/ 20=3, 3 11*4/ 20=2, 2 11*5/ 20=2, 75 9*6/ 20=2, 7 9*4/ 20=1, 8 9*5/ 20=2, 25 Si sottraggono alle frequenze osservate le frequenze teoriche e si elevano al quadrato, dividendo poi il risultato per le frequenze teoriche. (2 -3, 3) ²= 1, 69 (4 -2, 7) ²= 1, 69 (3 -2, 2) ²= 0, 64 (1 -1, 8) ²= 0, 64 (2 -2, 75) ²= 0, 56 (3 -2. 25) ²=0, 56 (4 -2, 75) ²=1, 56 (1 -2. 25) ²= 1, 56

CHI QUADRO ES 1. (2 -3, 3) ²= 1, 69 / 3, 3 =0, 51 (4 -2, 7) ²= 1, 69 /2, 7= 0, 62 (3 -2, 2) ²= 0, 64 /2, 2=0, 29 (1 -1, 8) ²= 0, 64/ 1, 8= 0, 35 (2 -2, 75) ²= 0, 56/ 2, 75=0, 21 (3 -2. 25) ²=0, 56/ 2. 25=0, 25 (4 -2, 75) ²=1, 56/ 2, 75=0, 57 (1 -2. 25) ²= 1, 56/ 2. 25=0, 69 χ2 =0, 51+0, 62+0, 29+0, 35+0, 21+0, 25+0, 57+0, 69= 3, 49 Un χ2 superiore a zero esclude l'ipotesi nulla, ma questo non ha molto significato in quanto esiste quasi sempre (o molto spesso) una qualche differenza tra le frequenze teoriche e le frequenze assegnate.

CHI QUADRO ES 1. Per vedere se il nostro chi quadro identifichi o meno una relazione significativa occorre calcolare i gradi di libertà che dipendono dal numero di celle contenute in una tabella. N. Di esami sostenuti g. d. l. = (r-1) (c-1) dove g = n dei gradi di libertà r = n delle righe C = n delle colonne Votazione media conseguita 21 25 27 30 TOT. COLONNA Studenti scienze educazione 2 3 2 4 11 Studenti STPPM 4 1 3 1 9 TOT. RIGA 6 4 5 5 N= 20 Nel nostro caso si avrà allora: g. d. l. = (2 -1) * (4 -1) =3

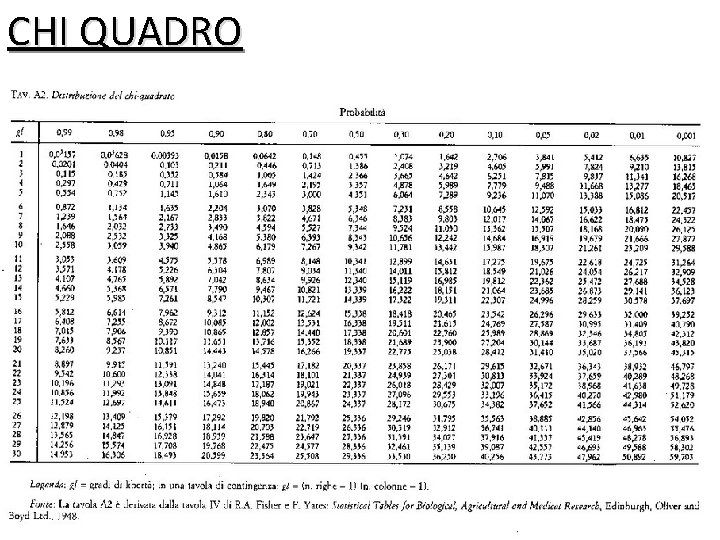
CHI QUADRO ES 1. Il livello di significatività viene solitamente stabilito a 0, 05. Dobbiamo adesso andare a vedere le tavole del χ2 considerando che i nostri g. d. l. sono 3

CHI QUADRO

CHI QUADRO Con 3 gradi di libertà, il valore di 3, 49 è inferiore al valore-limite previsto di 7, 815 e dunque la relazione non è statisticamente significativa avendo, appunto, un χ2 non significativo.