Also called generalized conformal supersymmetry with tensorial central

(Also called: generalized conformal supersymmetry with tensorial central charges; conformal M-algebra; osp spacetime supersymmetry) Particle content of models with parabose spacetime symmetry Igor Salom Institute of physics, University of Belgrade

Talk outline • What is this supersymmetry? • Connection with Poincaré (and super-conformal) algebras and required symmetry breaking • Unitary irreducible representations – What are the labels and their values? – How can we construct them and “work” with them? • Simplest particle states: – massless particles without “charge” – simplest “charged” particles

What is supersymmetry {Qa, Qb} = -2 i (gm)ab Pm, b generated by [symmetry Mmn, Qa] = -1/4 ([g m, gn])a Qb, [Pma , Q(Lie) a] = 0 superalgebra supersymmetry = ? ruled out in LHC? = Poincaré supersymmetry! HLS theorem – source of confusion?

But what else? {Qa, Qb }=0 {Qa, Qb }= 0 • in 4 spacetime dimensions: Tensorial central charges • in 11 spacetime dimensions: this is known as M-theory algebra • can be extended to super conformal case

+ supersymmetry: [Mmn, Qa] = -1/4 ([gm, gn])ab Qb, [Pm, Qa] = 0, {Qa, Qb} = -2 i (gm)ab Pm Simplicity as motivation? Poincaré space-time: Something Parabose algebra: else? + conformal symmetry: [Mmn, Mlr] = i (hnl Mmr + hmr[Mmn, Sa] = -1/4 ([gm, gn]) Mnl - hml Mnr - hnr Mml), {Sa, Sb} = -2 i (gm)ab Km, [Mmn, Pl] = i (- hnl Pm + hml Pn), [Km, Sa] = 0, [P m , P n ] = 0 hmn = 1 0 0 0 0 -1 b. S , a b + tens of additional relations spin • mass (momentum), • usual massless particles • “charged” particles carrying SU(2) x U(1) numbers • “elementary” composite particles from up to 3 charged subparticles mass (momentum), spin • a sort of parity asymmetry • …. (flavors, . . . )?

Parabose algebra • Algebra of n pairs of mutually adjoint operators satisfying: , and relations following from these. • Generally, but not here, it is related to parastatistics. • It is generalization of bose algebra:

Close relation to orthosymplectic superalgebra • Operators form osp(1|2 n) superalgebra. • osp generalization of supersymmetry first analyzed by C. Fronsdal back in. From 1986 now on n = 4 • Since then appeared in different context: higher spin models, bps particles, branes, M-theory algebra • mostly n=16, 32 (mostly in 10 or 11 space-time dimensions) • we are interested in n = 4 case that corresponds to d=4.

Change of basis - step 1 of 2 • Switch to hermitian combinations consequently satisfying “para-Heisenberg” algebra:

Change of basis - step 2 of 2 • define new basis for expressing parabose anticommutators: • we used the following basis of 4 x 4 real matrices: – 6 antisymmetric: , , – 10 symmetric matrices: ,

Generalized conformal superalgebra Connection with standard conformal algebra: of Y 1 = Y 2 = N 11 = N 21 = P 11 = P 21 = K 11 = KChoice 21 ≡ 0 basis {Qa, Qb }={Sa, Sb }= 0 + bosonic part of algebra

Unitary irreducible representations • only “positive energy” UIRs of osp appear in parabose case, spectrum of operator is bounded from below. Yet, they were not completely known. • states of the lowest E value (span “vacuum” subspace) are annihilated by all , and carry a representation of SU(n) group generated by (traceless) operators. • thus, each parabose UIR is labeled by an unitary irreducible representation of SU(n), labels s 1, s 2, s 3, and value of a (continuous) parameter – more often it is so called “conformal weight” d than E. • allowed values of parameter d depend upon SU(n) labels, and were not completely known – we had to find them!

Allowed d values expressions • In general, d has continuous and discrete parts ofthat must vanish and thus turn spectrum: into equations of motion within representation – continuous: d > d 1 ← LW Verma module is airreducible – discrete: d = d 1, d 2, d 3, … dk ← submodules must be factored out • points in discrete spectrum may arrise due to: – singular vectors ← quite understood, at known values of d – subsingular vectors ← exotic, did require computer analysis! • Discrete part is specially interesting for (additional) equations of motion, continuous part might be nonphysical (as in Poincare case)

Verma module structure • superalgebra structure: osp(1|2 n) root system, positive roots , defined PBW ordering • – lowest weight vector, annihilated by all negative roots • Verma module: • some of vectors – singular and subsingular – again “behave” like LWV and generate submodules • upon removing these, module is irreducible

s 1=s 2=s 3=0 (zero rows) e. g. this one will turn into and massless Dirac equation! • d = 0, trivial UIR • d = 1/2, these vectors are of zero (Shapovalov) norm, and thus must be factored out, i. e. set to zero to get UIR • d = 1, • d = 3/2, • d > 3/2 3 discrete “fundamentally scalar” UIRs In free theory (at least) should be no motion equations put by hand

s 1=s 2=0, s 3>0 (1 row) this UIR class will turn out to have additional SU(2)x. U(1) quantum numbers, the rest are still to be investigated • d = 1 + s 3/2, • d = 3/2 + s 3/2, • d = 2 + s 3/2, • d > 2 + s 3/2 3 discrete families of 1 -row UIRs, in particular 3 discrete “fundamental spinors” (first, i. e. s 3=1 particles).

s 1=0, s 2>0, s 3 ≥ 0 (2 rows) • d = 2 + s 2/2 + s 3/2, • d = 5/2 + s 2/2 + s 3/2, • d > 5/2 + s 2/2 + s 3/2 2 discrete families of 2 -rows UIRs

s 1>0, s 2 ≥ 0, s 3 ≥ 0 (3 rows) • d = 3 + s 1/2 + s 2/2 + s 3/2, • d > 3 + s 1/2 + s 2/2 + s 3/2 single discrete familiy of 3 -rows UIRs (i. e. discrete UIR is determined by Young diagram alone)

How to do “work” with these representations? • solution: realize UIRs in Green’s ansatz! • automatically: (sub)singular vectors vanish, unitarity guaranteed • for “fundamentally scalar” (unique vacuum) UIRs Greens ansatz was known • we generalized construction for SU nontrivial UIRs

Green’s ansatz representations • Now we have only ordinary Green’s ansatz of order p (combined with Klain’s transformation): bose operators and everything commutes! • we introduced 4 p pairs of ordinary bose operators: • and “spinor inversion” operators that can be constructed as 2 pi rotations in the factor space: • all live in product of p ordinary 4 -dim LHO Hilbert spaces: • p = 1 is representation of bose operators

“Fundamentally scalar UIRs” • d = 1/2 p = 1 – this parabose UIR is representation of ordinary bose operators – singular vector identically vanishes • d=1 p=2 – vacuum state is multiple of ordinary bose vacuums in factor spaces: • d = 3/2 p = 3 – vacuum:

1 -row, d = 1 + s 3/2 UIR This class of UIRs exactly constitutes p=2 Green’s ansatz: • Define: • – two independent pairs of bose operators • are “vacuum generators”: s 3 • All operators will annihilate this state:

“Inner” SU(2) action • Operators: generate an SU(2) group that commutes with action of the Poincare (and conformal) generators. • Together with the Y 3 generated U(1) group, we have SU(2) x U(1) group that commutes with observable spacetime symmetry and additionally label the particle states.

1 -row, other UIRs • Other “families” are obtained by increasing p: – d = 3/2 + s 3/2, p = 3, s 3 – d = 2 + s 3/2, p = 4 s 3 • Spaces of these UIRs are only subspaces of p = 3 and p = 4 Green’s ansatz spaces

2 -rows UIRs • Two “vacuum generating” operators must be antisymmetrized we need product of two p=2 spaces. • To produce two families of 2 -rows UIRs act on a natural vacuum in p=4 and p=5 by:

3 -rows UIRs • Three “vacuum generating” operators must be antisymmetrized we need product of three p=2 spaces. • Single family of 3 -rows UIRs is obtained by acting on a natural vacuum in p=6 by:

Conclusion so far • All discrete UIRs can be reproduced by combining up to 3 “double” 1 -row spaces (those that correspond to SU(2)x. U(1) labeled particles)

Simplest nontrivial UIR - p=1 • Parabose operators act as bose operators and supersymmetry generators Qa and Sb satisfy 4 -dim Heisenberg algebra. • Hilbert space is that of 4 -dim nonrelativistic quantum mechanics. We may introduce equivalent of coordinate or momentum basis: • Yet, these coordinates transform as spinors and, when symmetry breaking is assumed, three spatial coordinates remain.

Simplest nontrivial UIR - p=1 • Fiertz identities, in general give: • where: • since generators Q mutually comute in p=1, all states are massless: • in p=1, Y 3 becomes helicity: • states are labeled by 3 -momentum and helicity:

Simplest nontrivial UIR - p=1 • introduce “field states” as vector coherent states: source of equations of motion can be traced back to the corresponding • derive familiar results: singular vector

Next more complex class of UIR: p=2 • Hilbert space is mathematically similar to that of two (nonidentical) particles in 4 -dim Euclidean space • However, presence of inversion operators in complicates eigenstates. • In turn, mathematically most natural solution becomes to take complex values for Qa and Sa.

Space p=2 • Fiertz identities: • where: • only the third term vanishes, leaving two mass terms! Dirac equation is affected.

Space p=2 • Massive states are labeled by Poincare numbers (mass, spin square, momentum, spin projection) but also Y 3 value, and q. numbers of SU(2) group generated by T 1 , T 2 and T 3. • square of this “isospin” coincides with square of spin. • Similarly, massless states also have additional U(1)x. SU(2) quantum numbers.

Conclusion • • Simple in statement but rich in properties Symmetry breaking of a nice type Promising particle structure Many predictions but yet to be calculated A promising type of supersymmetry!

Thank you for your attention!

A simple relation in a complicated basis

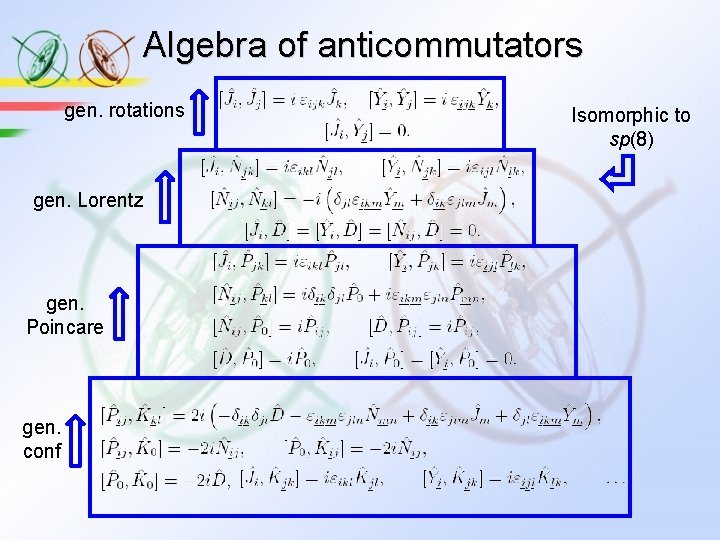
Algebra of anticommutators gen. rotations gen. Lorentz gen. Poincare gen. conf Isomorphic to sp(8)

Symmetry breaking J 1 J 2 J 3 Y 1 N 12 N 13 Y 2 N 21 N 22 N 23 Y 3 N 31 N 32 N 33 D P 0 {Q, Q} {Q, S} operators K 0 P 11 P 12 P 13 K 11 K 12 K 13 P 21 P 22 P 23 K 21 K 22 K 23 P 31 P 32 P 33 K 31 K 32 K 33 operators {S, S} operators

Symmetry breaking D J 1 J 2 J 3 {Q, S} operators ? Potential ~(Y 3)2 P 0 {Q, Q} operators P 1 Y 3 N 1 N 2 C(1, 3) conformal algebra N 3 K 0 P 2 P 3 {S, S} K 1 operators K 2 K 3