The decimal system also called the base 10

The decimal system, also called the base 10 number system is based on ten numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. All the numbers are formed by combination of these 10 numbers -> to form a 2 digit number, the second digit is multiplied by 10. 15 is equal to (1 X 10) + 5. To form a 3 -digit number, the third digit is multiplied by 100. This concept continues with the next digit multiplied by 1000, the next by 10, 000, and so on. A number like 8679 would be calculated as (8 X 1000) + (6 X 100) + (7 X 10) + (9 X 1). Or More generally, decimal or base 10 notation is based on the fact that any positive integer can be written uniquely as sum of products of the form Where each n is a nonnegative integer (0 and above) and each d is one of the 10 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 This concept is easy to grasp, because we use the decimal system in every day applications. Kavita Hatwal Fall 2002 1

But the computers use base 2 or binary notation. The signals used in modern electronics are always in one of only two states->0, 1. Just like in decimal any positive integer can be written uniquely as sum of products of the form where 10 is the base Similarly in binary or base 2 notation, any positive integer can be written uniquely as sum of products of the form where 2 is the base Example Kavita Hatwal Fall 2002 2

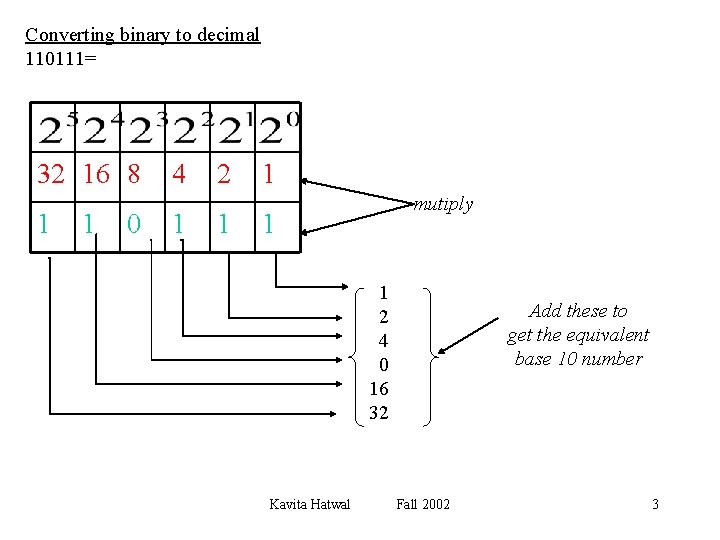
Converting binary to decimal 110111= 32 16 8 1 1 0 4 1 2 1 1 mutiply 1 1 2 4 0 16 32 Kavita Hatwal Add these to get the equivalent base 10 number Fall 2002 3

Converting decimal to binary To convert a base 10 number into base 2, repeatedly divide the number by 2 till the quotient is 0 and keep collecting the remainders at each step Divisor Quotient Remainder 2 35 1 2 17 1 2 8 0 2 4 0 2 2 0 2 1 1 Collect these starting from the bottom So the binary equivalent of 35 is 100011 0 Kavita Hatwal Fall 2002 4

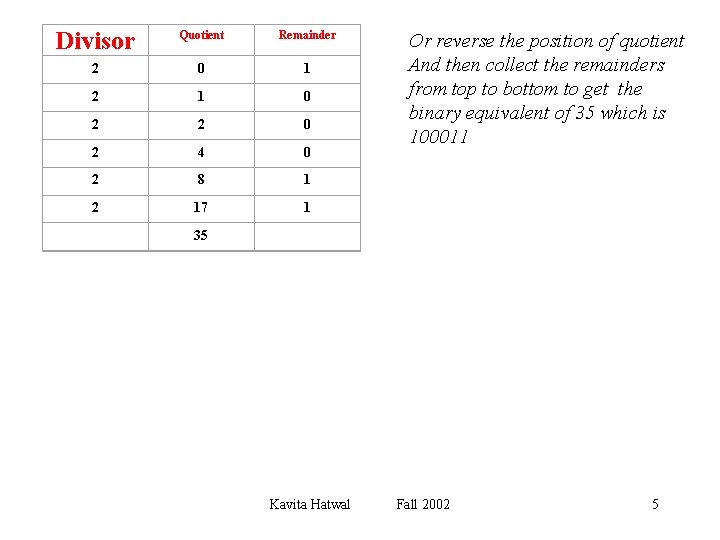
Divisor Quotient Remainder 2 0 1 2 1 0 2 2 0 2 4 0 2 8 1 2 17 1 Or reverse the position of quotient And then collect the remainders from top to bottom to get the binary equivalent of 35 which is 100011 35 Kavita Hatwal Fall 2002 5

Binary addition is similar to decimal addition in the sense that you start adding the addends proceeding from right to left. But the numbers that you’re allowed to use are only 0 and 1. Rules for binary addition 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 0, carry over 1 1+1+1 = 1, carry over 1 Add 10101 + 11100 If the carry goes on beyond the maximum number of bits, then an overflow has occurred. Page 73, # 14 Kavita Hatwal Fall 2002 6

Negative number representation in binary notation Earlier it was decided to make the leftmost bit the sign bit ->1 denotes a negative number and 0 in that bit position indicates a positive number. So 6 = 0110 (in binary) and -6 = 1110 But this led to complications like if we add 6 and – 6, we should get 0, but what do we get? Try it out To avoid this and many other complications like non unique representation of 0, adding a negative and a positive number etc, an easier way called the two’s complement was adopted in which leading 0’s means a positive number and leading 1’s means a negative number. So in two’s complement land, for a fixed 4 -bit space, we read for negative integers Page 73, #25 Kavita Hatwal Fall 2002 7

To find the 8 -bit two’s complement of a positive integer a that is at most 255 • Write the 8 -bit binary representation for a. • Switch all the 1’s to 0’s and 0’s to 1’s • Add 1 in binary notation. Page 74, # 21 Two’s complement is extra handy when representing negative integers and performing addition and subtraction on signed integers. The 8 -bit binary representation for a This knowledge comes handy when we’ve to do subtraction or addition of two different signed numbers • Convert both integers to their 8 bit representations. • Add using binary addition • Truncate any leading 1’s that occur in the rightmost (2^8) position. • Convert the sum back to decimal form interpreting leading o’s as +ve and leading 1’s as -ve Page 73, # 31 Kavita Hatwal Fall 2002 8

Hexadecimal notation The cool thing about Hexadecimal (base 16) is that we save space writing long binary numbers and also it is very easy to convert from hexadecimal to binary, since almost all computer data are multiples of 4. Similarly in hexadecimal or base 16 notation, any positive integer can be written uniquely as sum of products of the form To convert from hexadecimal to binary and vice versa just remember table 1. 5. 3 on page 71. Use that table to convert • E 0 D into binary • 011011111000101 into hexadecimal E 0 D 1110 0000 1101 0011 0111 1100 0101 3 7 C 5 Juxtapose the results Kavita Hatwal Fall 2002 9