Algorithmes et structures de donnes avances Cours 123

Algorithmes et structures de données avancées Cours 1+2+3 Patrick Reuter maître de conférences http: //www. labri. fr/~preuter

Déroulement • CM mardi 8 h 30 – 9 h 30 • TD/TP en alternance mardi de 10 h 00– 11 h 30

Motivation • Niklaus Wirth, ETH Zuerich, 1976 « Algorithms + Data Structures = Programs »

Motivation Structure de donnée: p. ex. fantôme - couleur - position - direction - aggressif ou pas ? Algorithmes: p. ex. mettre a jour le meilleur score

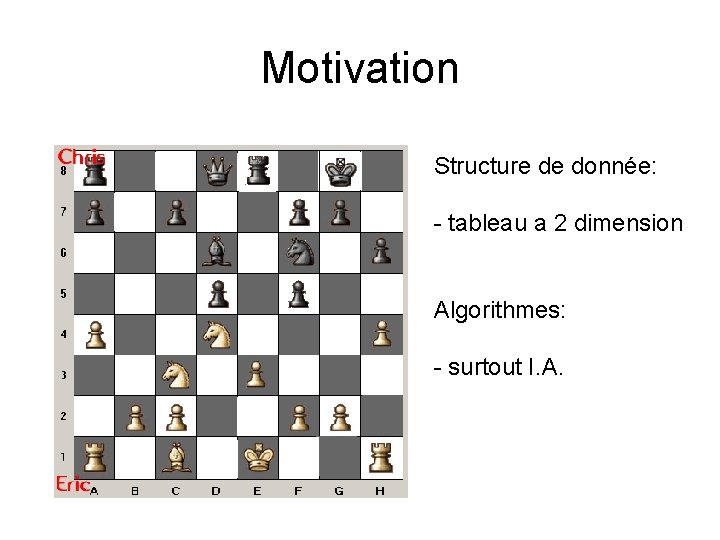
Motivation Structure de donnée: - tableau a 2 dimension Algorithmes: - surtout I. A.

Motivation Structure de donnée : Pile LIFO (Last In First Out)

Motivation Structure de donnée : File FIFO (First In First Out) Aussi: File à priorité

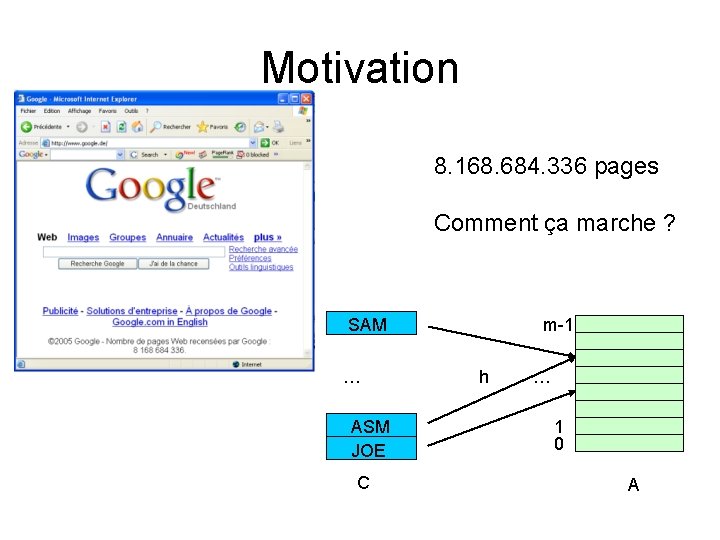
Motivation 8. 168. 684. 336 pages Comment ça marche ? SAM … ASM JOE C m-1 h … 1 0 A

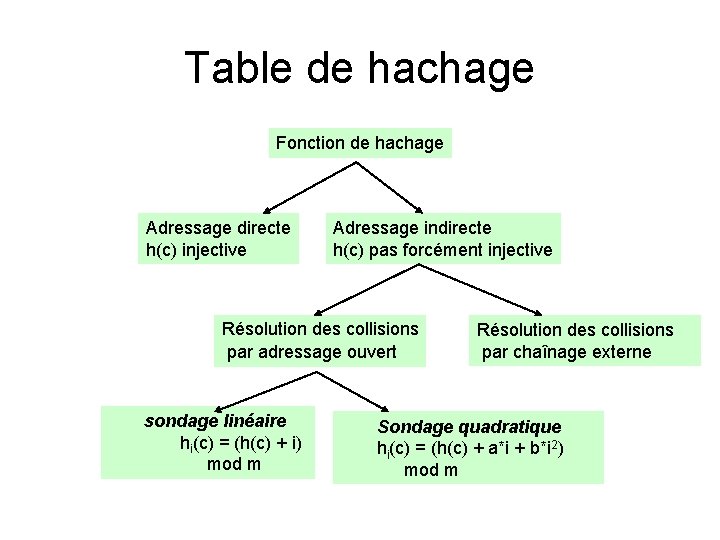
Table de hachage Fonction de hachage Adressage directe h(c) injective Adressage indirecte h(c) pas forcément injective Résolution des collisions par adressage ouvert sondage linéaire hi(c) = (h(c) + i) mod m Résolution des collisions par chaînage externe Sondage quadratique hi(c) = (h(c) + a*i + b*i 2) mod m

ASDA • Nouvelles structures de données – Arbres – Graphes • Preuves • Récursivité/Récurrence • Théorie de la complexité • …

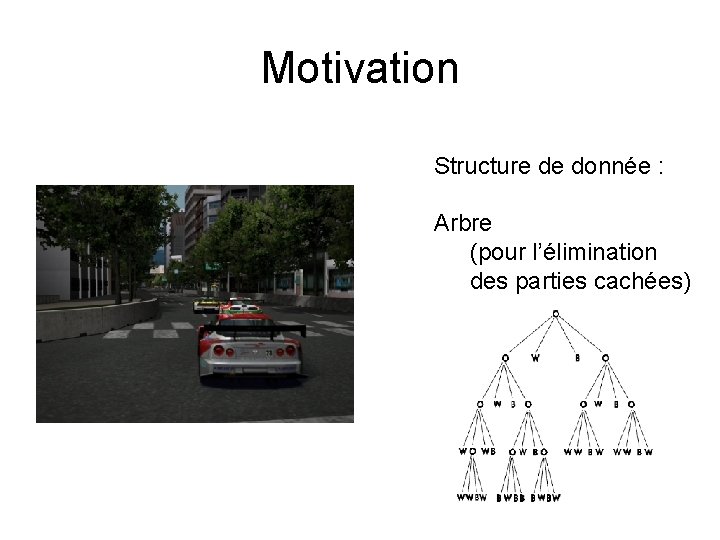
Motivation Structure de donnée : Arbre (pour l’élimination des parties cachées)

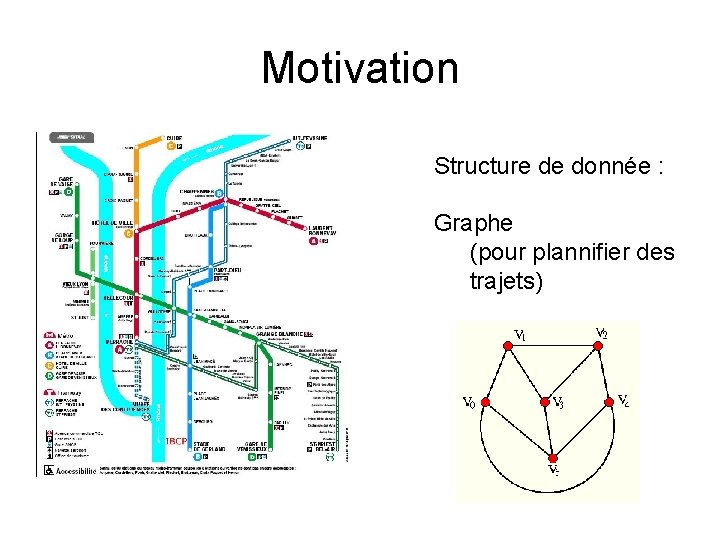
Motivation Structure de donnée : Graphe (pour plannifier des trajets)

Rappel sur la récurrence

Factoriel • • 0! = 1 1! = 1 2! = 1*2 3! = 1*2*3 4! = 1*2*3*4 5! = 1*2*3*4*5 6! = 1*2*3*4*5*6 n! = 1*2*3*4*5*6*. . * (n-1) * n

Factoriel • Deux manières de faire : – Itératif – Récursif

Itératif fonction factoriel. Boucle(n : integer): integer; var i, res : integer; début res : = 1; i : = 1; tant que i<=n faire res : = res * i; i : = i + 1; fin tant que result : = res; fin

Rappel Fonction définie par récurrence Une fonction définie par récurrence se caractérise par deux propriétes : • La fonction est définie par elle-meme, c-à-d. la fonction appelle-meme dans le corps de la fonction • L’appel (ou les appels) de la fonction par ellememe est isolé par une condition, la condition d’arret, pour éviter les appels infinis.

Sondage function factoriel(n : integer) : integer; var resultat : integer; begin if (n = 0) OR (n = 1) then resultat : = 1 else resultat : = n * factoriel(n-1); result : = resultat; end;

Sondage function factoriel(n : integer) : integer; var resultat : integer; begin if (n = 0) OR (n = 1) then resultat : = 1 else resultat : = n * factoriel(n-1); result : = resultat; end;

Sondage function factoriel(n : integer) : integer; var resultat : integer; begin Condition d’arrêt : la fonction n’est plus appelé par elle-même if (n = 0) OR (n = 1) then resultat : = 1 else resultat : = n * factoriel(n-1); result : = resultat; end;

Sondage function factoriel(n : integer) : integer; var resultat : integer; begin Condition d’arrêt : la fonction n’est plus appelé par elle-même if (n = 0) OR (n = 1) then resultat : = 1 else resultat : = n * factoriel(n-1); result : = resultat; Appel de la fonction par elle-même end;

Sondage function factoriel(n : integer) : integer; var resultat : integer; begin Write. Ln(‘debut de fonction : n = ‘, n); if (n = 0) OR (n = 1) then resultat : = 1 else resultat : = n * factoriel(n-1); Write. Ln(‘fin de fonction : resultat = ‘, resultat); result : = resultat; end

• Appel de fonction : factoriel(5); • • • factoriel : = 5 * factoriel(5 - 1); factoriel : = 5 * (4 * factoriel(4 - 1)); factoriel : = 5 * (4 * (3 * factoriel(3 - 1))); factoriel : = 5 * (4 * (3 * (2 * factoriel(2 - 1)))); factoriel : = 5 * (4 * (3 * (2 * (1 ))));

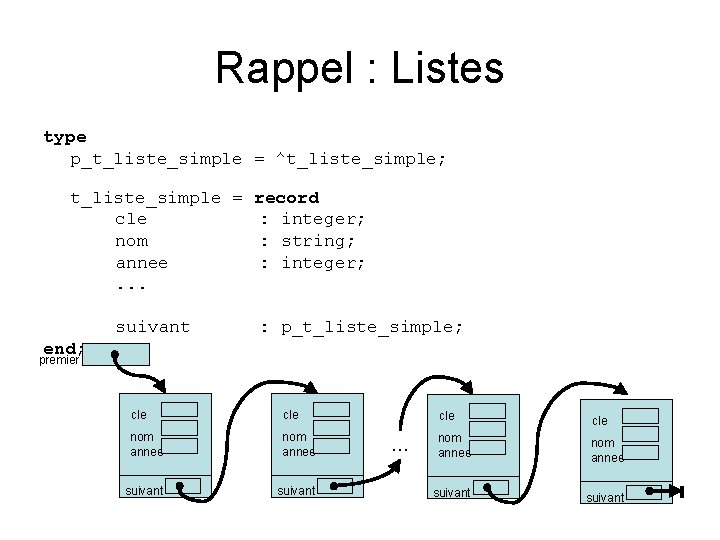
Rappel : Listes type p_t_liste_simple = ^t_liste_simple; t_liste_simple = record cle : integer; nom : string; annee : integer; . . . suivant : p_t_liste_simple; end; premier cle nom annee suivant … cle nom annee suivant

Afficher tous les éléments • Itératif • Récursif

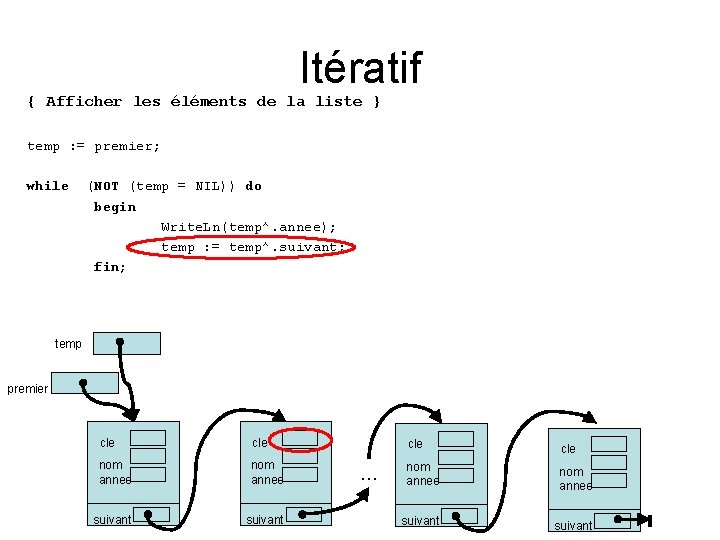
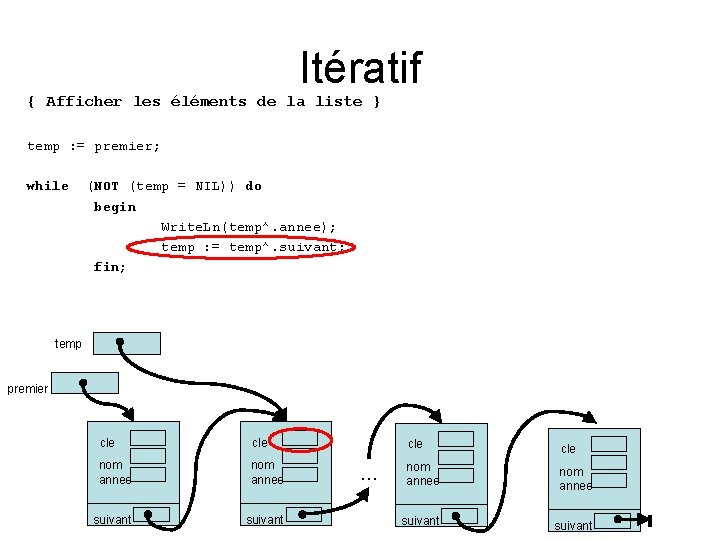
Itératif { Afficher les éléments de la liste } temp : = premier; while (NOT (temp = NIL)) do begin Write. Ln(temp^. annee); temp : = temp^. suivant; fin; temp premier cle nom annee suivant … cle nom annee suivant

Itératif { Afficher les éléments de la liste } temp : = premier; while (NOT (temp = NIL)) do begin Write. Ln(temp^. annee); temp : = temp^. suivant; fin; temp premier cle nom annee suivant … cle nom annee suivant

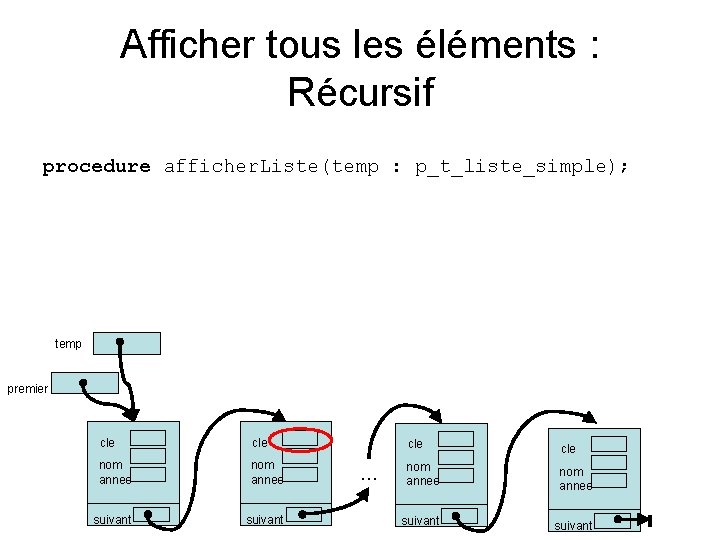
Afficher tous les éléments : Récursif procedure afficher. Liste(temp : p_t_liste_simple); temp premier cle nom annee suivant … cle nom annee suivant

Afficher tous les éléments procedure afficher. Liste(temp : p_t_liste_simple); begin if (temp <> NIL) then begin Write. Ln('Element annee : ', temp^. annee); afficher. Liste(temp^. suivant); end;

Sondage … • Recherche linéare dans un tableau non-trié – O(n) • Recherche linéare dans une liste non-trié – O(n) • Recherche dans un tableau trié – O(log n) (par dichotomie) • Recherche dans une liste triée – O(n) • Table de Hachage HT – Suivant la fonction de hachage h(t), au mieux O(1), au pire O(n)

Complexité asymptotique Chercher Ajouter Enlever Tableau non trié: O(n) O(1) O(lg n) O(n) O(1) Liste non triée: Tableau trié: Liste trié : Arbre binaire:

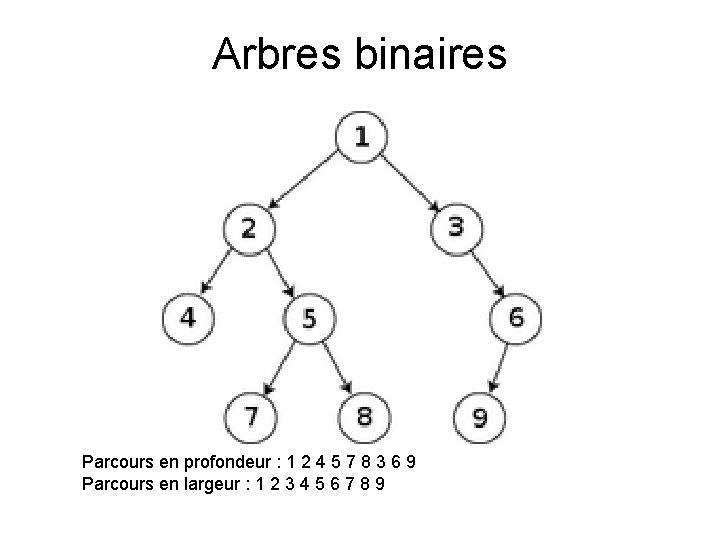
Arbres binaires Parcours en profondeur : 1 2 4 5 7 8 3 6 9 Parcours en largeur : 1 2 3 4 5 6 7 8 9

Arbres binaires - structure de données qui peut se représenter sous la forme d'une hiérarchie - chaque élément est appelé nœud - le nœud initial est appelé racine. - chaque nœud possède au plus deux éléments fils au niveau inférieur, habituellement appelés fils gauche et fils droit. - l'élément d’un nœud fils au niveau supérieur est appelé père. - au niveau le plus élevé, il y a donc un nœud racine. - un nœud n'ayant aucun fils est appelé feuille. - les nœuds ayant au moins un fils sont appelés nœuds internes. - le nombre de niveaux total, autrement dit la distance entre la feuille la plus éloignée et la racine est appelé profondeur ou hauteur de l'arbre. Autrement dit : La hauteur d'un arbre est la longueur du plus grand chemin de la racine à une feuille. -

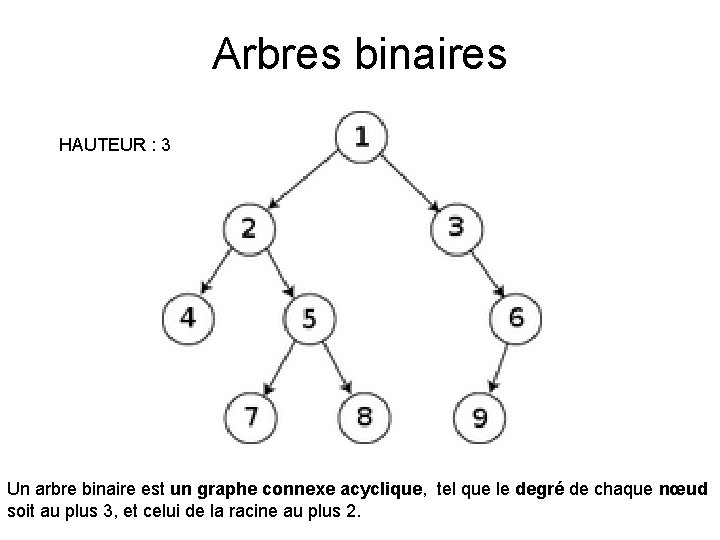
Arbres binaires HAUTEUR : 3 Un arbre binaire est un graphe connexe acyclique, tel que le degré de chaque nœud soit au plus 3, et celui de la racine au plus 2.

Arbres binaires • Arbre binaire entier est un arbre dont tous les nœuds possèdent zéro ou deux fils. • Arbre binaire parfait (complet) est un arbre binaire entier dans lequel toutes les feuilles sont à la même distance de la racine. – – • Un arbre binaire complet de hauteur h contient donc 2 h+1 -1 nœuds, et son nombre de feuilles est : Fh = 2 h. Arbre binaire dégénéré est un arbre binaire dans lequel tous ses noeuds n'ont qu'un seul descendant.

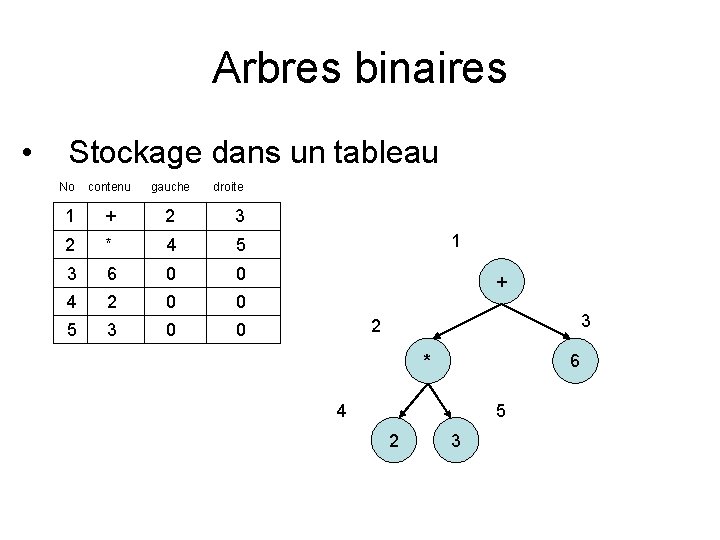
Arbres binaires • Stockage dans un tableau No contenu gauche droite 1 + 2 3 2 * 4 5 3 6 0 0 4 2 0 0 5 3 0 0 1 + 3 2 * 6 4 5 2 3

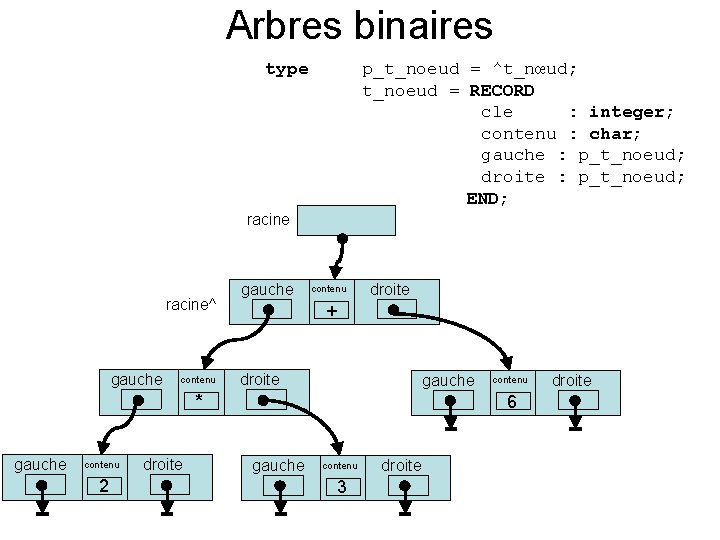
Arbres binaires type p_t_noeud = ^t_nœud; t_noeud = RECORD cle : integer; contenu : char; gauche : p_t_noeud; droite : p_t_noeud; END; racine^ gauche contenu +2 contenu +* droite 3 gauche contenu ++ droite 3 droite gauche 3 gauche contenu +3 droite 3 contenu +6 droite 3

Arbres binaires Méthode d'itération des arbres binaires • • • Préfixe, Postfixe, Infixe

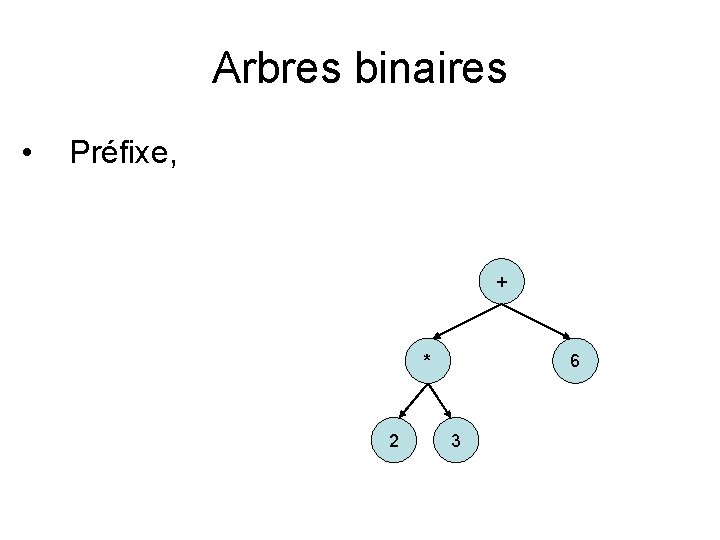
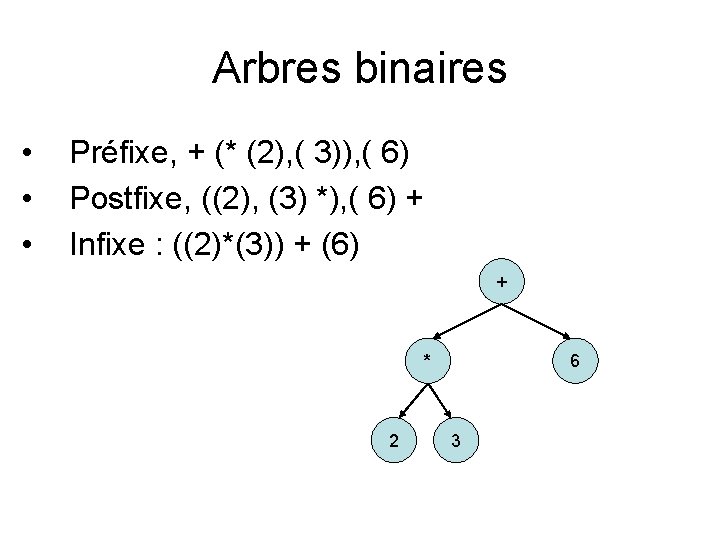
Arbres binaires • Préfixe, + * 2 6 3

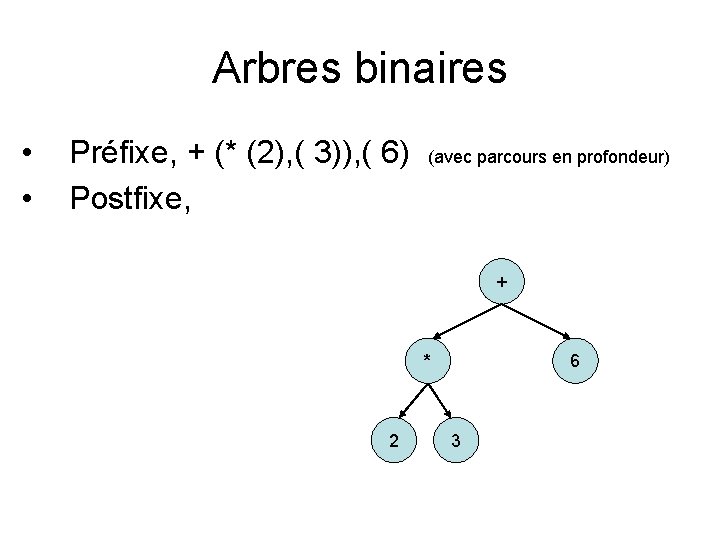
Arbres binaires • • Préfixe, + (* (2), ( 3)), ( 6) Postfixe, (avec parcours en profondeur) + * 2 6 3

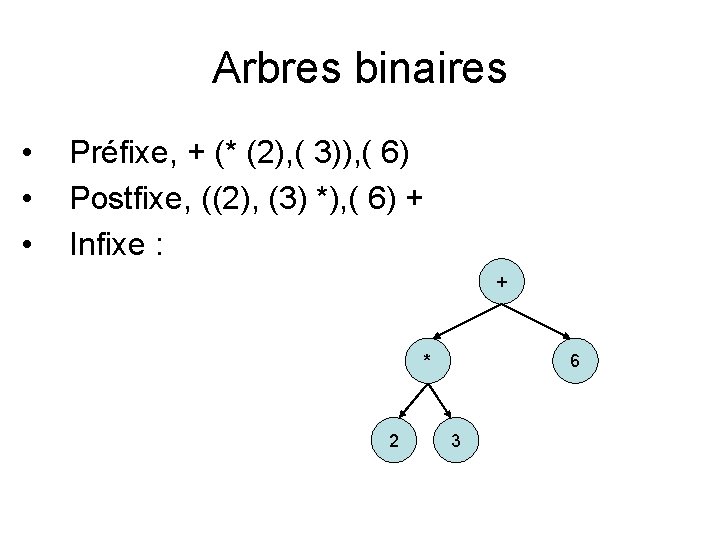
Arbres binaires • • • Préfixe, + (* (2), ( 3)), ( 6) Postfixe, ((2), (3) *), ( 6) + Infixe : + * 2 6 3

Arbres binaires • • • Préfixe, + (* (2), ( 3)), ( 6) Postfixe, ((2), (3) *), ( 6) + Infixe : ((2)*(3)) + (6) + * 2 6 3

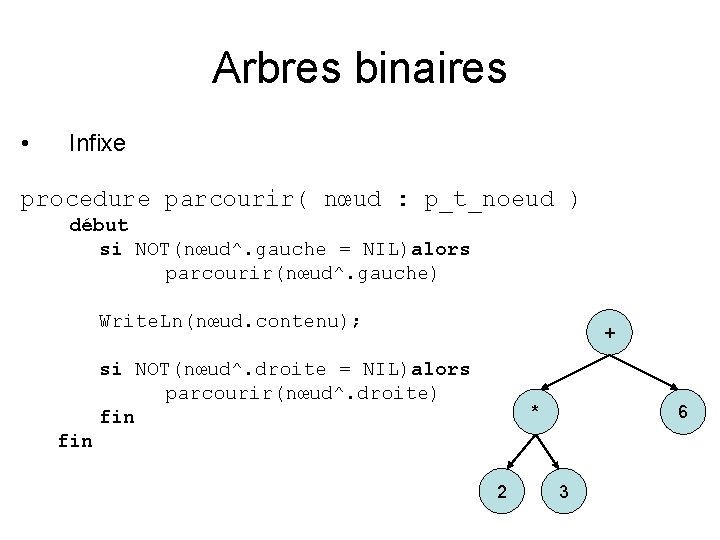
Arbres binaires • Infixe procedure parcourir( nœud : p_t_noeud ) début si NOT(nœud^. gauche = NIL)alors parcourir(nœud^. gauche) Write. Ln(nœud. contenu); + si NOT(nœud^. droite = NIL)alors parcourir(nœud^. droite) fin * 6 fin 2 3

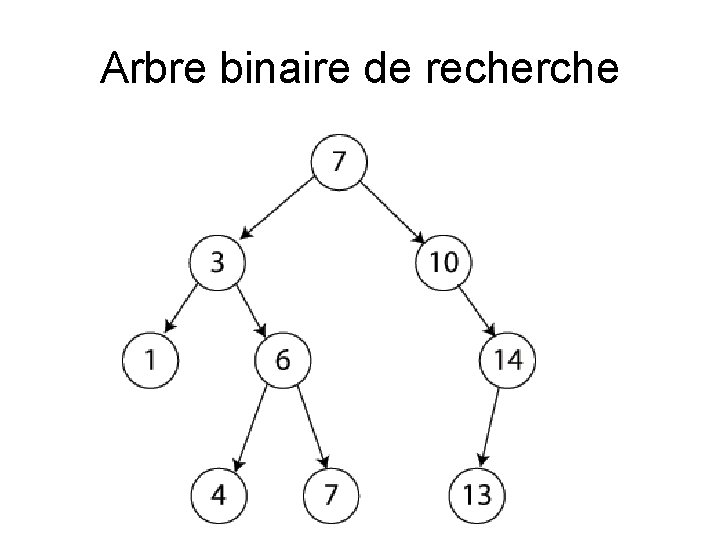
Arbre binaire de recherche

Arbre binaire de recherche • un arbre binaire dans lequel – chaque nœud possède une clé, – telle que chaque nœud du sous-arbre gauche ait une clé inférieure ou égale à celle du nœud considéré, – et que chaque nœud du sous-arbre droit possède une clé supérieure ou égale à celle-ci – Les nœuds que l'on ajoute deviennent des feuilles de l'arbre. – on pourra interdire ou non des clés de valeur égale.

Complexité asymptotique Arbre balancé AVL Arbre non balancé Trouver: O(lg n) O(n) Insérer: O(lg n) O(n) Enlever: O(lg n) O(n)

Arbre binaire balancé • Arbre balancé AVL – nommé selon ses auteurs – [Andelson-Velskii et Landis, 1962] – Pour chaque nœud, la hauteur du sous-arbre gauche (SAG) et du sous-arbe droite (SAD) diffèrent au plus de un

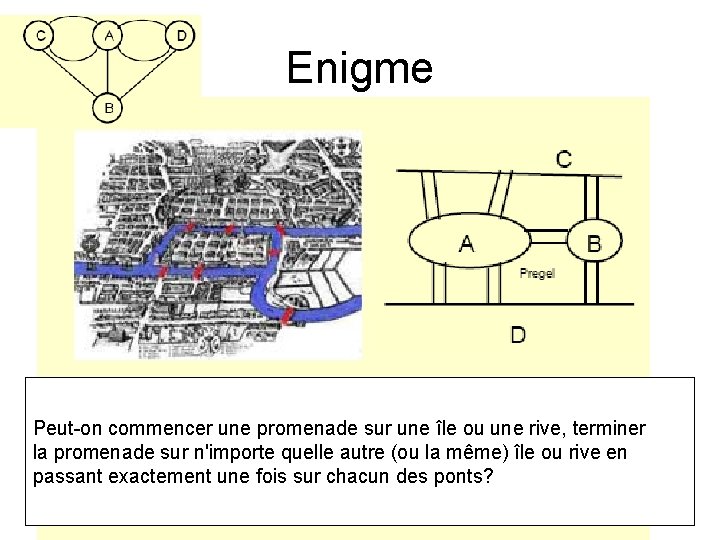
Enigme Peut-on commencer une promenade sur une île ou une rive, terminer la promenade sur n'importe quelle autre (ou la même) île ou rive en passant exactement une fois sur chacun des ponts?