Algorithmes et structures de donnes avances Cours 7

Algorithmes et structures de données avancées Cours 7 Patrick Reuter http: //www. labri. fr/~preuter

Les graphes • Un graphe G = (V, E) un couple de deux ensembles – Un ensemble V(G) = {v 1, v 2, …, vn} de sommets (anglais : one vertex, two vertices) – Un ensemble E(G) V x V d’arêtes (anglais : edges)

Définitions • Orientation : – les graphes non orientés – les graphes orientés • degré • boucle • parité (sommets pairs et impairs) • adjacence, voisin et voisinage • sommet isolé • sous-graphe, clique • Graphe régulier • Graphe complet • Isomorphisme • Chaîne, chaîne simple, cycle • Connexité • Stockage des graphes

Matrice d’adjacence • Pour des graphes orientés et non-orientés • Soit G = (V, E) avec V = {s 1, s 2, …, sn} • La matrice d’adjacence A est une matrice quadratique binaire de taille n x n avec Ai, k = 1 si (si, sk) E, Ai, k = 0 sinon • La matrice d’adjacence d’un graphe non orienté est symétrique • Suivant l’ordre des nœuds, il y a plusieurs matrice d’adjacence du même graphe

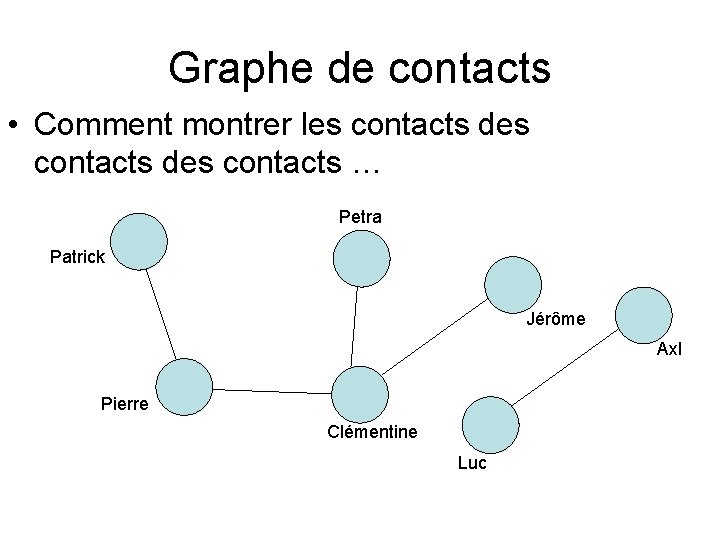
Graphe de contacts • Comment montrer les contacts des contacts … Petra Patrick Jérôme Axl Pierre Clémentine Luc

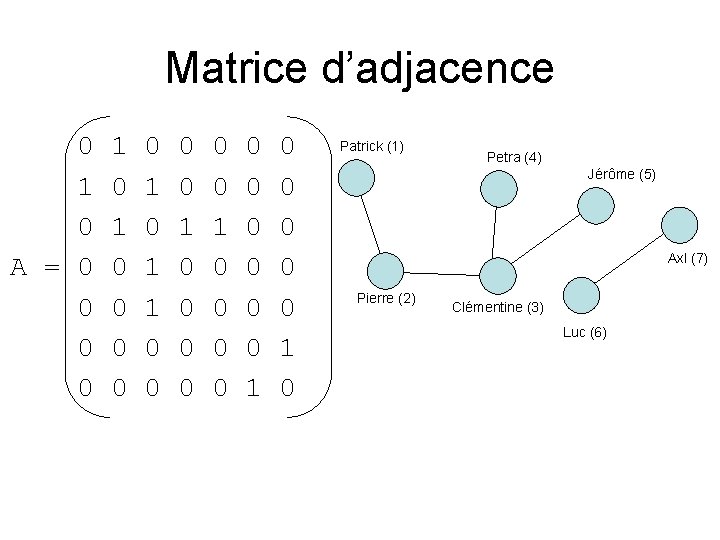
Matrice d’adjacence 0 1 0 A = 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0 Patrick (1) Petra (4) Jérôme (5) Axl (7) Pierre (2) Clémentine (3) Luc (6)

Fermeture transitive • La fermeture transitive d’un graphe G est le Graphe G* = (V, E* ), où une arête (i, j) є E ssi il y a une chaîne de i à j. + + + • Si les chaînes de longueur 0 sont aussi considérées, le résultat est la fermeture transitive et réflexive G*.

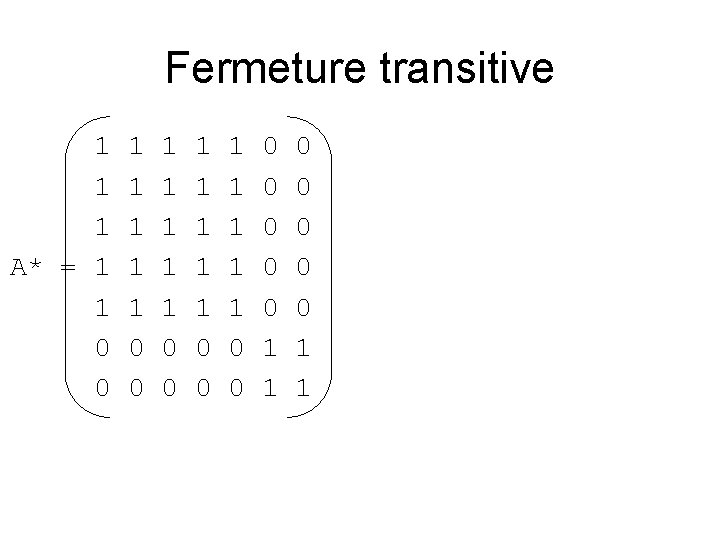
Fermeture transitive 1 1 1 A* = 1 1 0 0 1 1 1 1 1 0 0 0 0 1 1

Fermeture transitive • • A : Matrice d’adjacence Pour une chaîne maximale de longueur n Matrice d’adjacence de la fermeture transitive

• G(V, E) : (Matrice d’adjacence A): – Ai, k = 1 si (si, sk) E, Ai, k = 0 sinon • G*(V, E*) : Fermeture transitive de G (Matrice d’adjacence A*) – A*i, k = 1 ssi il y a une chaîne de si à sk.

Logiciels pour le calcul scientifique – Maple – Matlab – Mathematica – Mupad – Scilab –…

Mu. Pad • Démonstration

Algorithme de Warshall • permet de construire la fermeture transitive d'un graphe orienté ou non orienté.

Algorithme de Warshall • À partir de la matrice d'adjacence A du graphe G(V, E), on va calculer la matrice d'adjacence A* de G*(V, E*) • On suppose que Ak[i, j] représente l'existence d'une chaîne de i à j passant uniquement par des sommets inférieurs ou égaux à k. Ak[i, j]=Ak-1[i, j] OU (Ak-1[i, k] ET Ak-1[k, j]) • Il existe donc une chaîne de i à j passant seulement par des sommets inférieurs ou égaux à k – s'il existe une chaîne de i à j passants seulement par des sommets inférieurs ou égaux à k-1 – ou alors s'il existe une chaîne de i à k passant par des sommets inférieurs ou égaux à k-1 ET une chaîne de k à j passant par des sommets inférieurs ou égaux à k-1 • Matrice d’adajcence de G*: An[i, j]

Algorithme de Warshall Entrée : Matrice d’adjacence A pour k de 1 à |V(G)| faire pour i de 1 à |V(G)| faire pour j de 1 à |V(G)| faire if (A[i][j]=1 OU (A[i][k]=1 ET A[k][j]=1)) A[i][j]=1 else A[i][j]=0 A[i][j] = A[i][j] OU (A[i][k] ET A[k][j]) Sortie : A est la matrice décrivant la fermeture transitive

Algorithme de Warshall • Complexité – O(n 3) – il peut être intéressant de construire la fermeture transitive d'un graphe une fois pour toute, on peut savoir si les sommets si et sj appartiennent à la même composante connexe en un temps constant

• Peut-on utiliser la fermeture transitive pour tester si un graphe est connexe ?

Connexité • La notion de connexité exprime la possibilité d'aller de n'importe quel sommet du graphe à n'importe quel autre sommet du graphe. Plus formellement : • Un graphe G est connexe si et seulement si s, t V(G), il existe une chaîne entre s et t.

Graphe connexe/complet • Un graphe G est connexe si et seulement si s, t V(G), il existe une chaîne entre s et t. • Un graphe G est complet si et seulement si s, t V(G), il existe une arête entre s et t.

Récapitulatif des preuves • Preuve par récurrence • Preuve par contradiction • Preuve par construction

Preuve par induction ou preuve par récurrence • Une preuve par induction contient deux parties : – le cas de base – et la partie d'induction.

Preuve par contradiction Raisonnement par l’absurde : L’idée d’une telle preuve est de supposer que l’énoncé est fausse, puis de montrer que cette supposition conduit à une contradiction. Puisque la logique ne peut être contradictoire , c’est la supposition qui est fausse, et par conséquent l’énoncé est vrai.

Preuve par construction • Cette preuve nous prouve non seulement l'existence d'un objet, mais aussi une méthode pour le trouver • Une telle preuve est toujours plus appréciée par un informaticien qu'une preuve qui indique seulement qu'un objet existe. • La raison est que l'informaticien peut souvent convertir une preuve constructive en un algorithme pour trouver l'objet. • De manière générale, une preuve constructive est toujours plus convaincante qu'une preuve d'existence.

• Preuve No. 1 – Par récurrence

Théorème : • s V(G) d(s) = 2 | E(G) | « La somme de degrés de tous les sommets est égal à deux fois le nombre d’arêtes »

Technique de preuve par induction Preuve : • Vérifier que s V(G) d(s) = 2 | E(G) | pour un graphe sans arête • Supposer que s V(G) d(s) = 2 | E(G) | pour n'importe quel graphe avec au plus k arêtes, • Prouver que si s V(G) d(s) = 2 | E(G) | est vrai pour n'importe quel graphe avec au plus k arêtes, c'est aussi vrai pour n'importe quel graphe avec k+1 arêtes.

La preuve du théorème (1/2) • Par induction sur le nombre d'arêtes dans le graphe. – (cas de base) La propriété est trivialement vraie pour un graphe avec |E| = 0, car le degré de chaque sommet du graphe est 0. – (hypothèse d'induction) On suppose que pour un graphe G avec au moins un sommet et au plus k arêtes, s V(G) d(s) = 2 | E(G) |

La preuve du théorème (2/2) • (induction) Nous construisons un graphe G' en rajoutant une arête à G. • Les sommets extrémités de la nouvelle arête, disons s 1 et s 2 (il est possible que s 1 et s 2 soient le même sommet), vont avoir leur degré augmenté de 1 chacun. • Il est donc vrai que s V(G’) d(s) = s V(G) d(s) + 2. De plus, nous avons rajouté une arête dans G'. Par conséquent |E(G')| = |E(G)| + 1. • Donc, s V(G’) d(s) = s V(G) d(s) + 2 = 2|E(G)|+ 2 = 2(|E(G)| + 1) = 2|E(G')|. • Nous avons donc s V(G’) d(s) = 2|E(G')| Nous avons donc prouvé la propriété par récurrence.