Actors actor composition and an actor language describing

Actors, actor composition, and an actor language describing the semantics of (some) visual languages Jörn W. Janneck The Ptolemy Group University of California at Berkeley

credits Johan Eker, Lund University – language design, C code generation Yang Zhao, UCB – action-level scheduling Chris Chang, UCB – type system, program transformations Lars Wernli, ETH Zurich – Java code generation, generic code generation infrastructure Jörn W. Janneck 2 The Ptolemy Group University of California at Berkeley

What's an actor? u entity that has. . . – state – ports u . . . and is defined by. . . – outputs in response to inputs – state transition in response to inputs u data packaged into tokens Jörn W. Janneck 3 The Ptolemy Group University of California at Berkeley
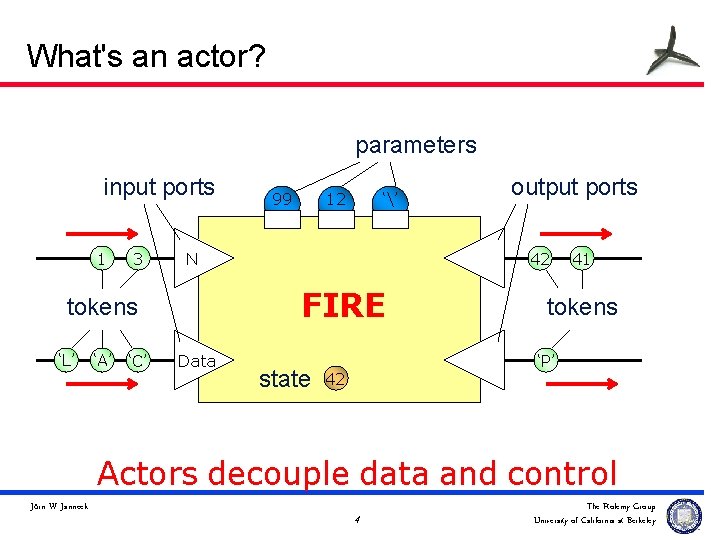
What's an actor? parameters input ports 1 3 ‘A’ ‘C’ 12 ‘’ N Data output ports 42 Actor FIRE tokens ‘L’ 99 state 41 tokens ‘P’ 42 Actors decouple data and control Jörn W. Janneck 4 The Ptolemy Group University of California at Berkeley
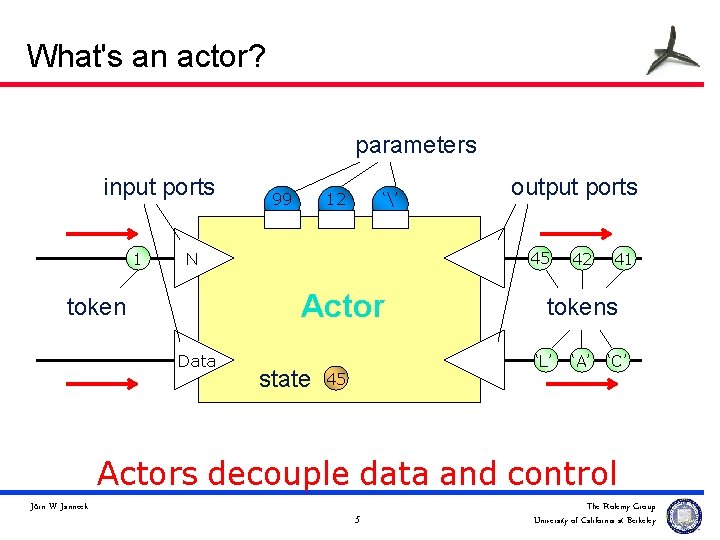
What's an actor? parameters input ports 1 99 12 ‘’ 45 2 N Actor token Data output ports state 41 tokens ‘P’ ‘L’ 45 42 4 ‘A’ ‘C’ Actors decouple data and control Jörn W. Janneck 5 The Ptolemy Group University of California at Berkeley
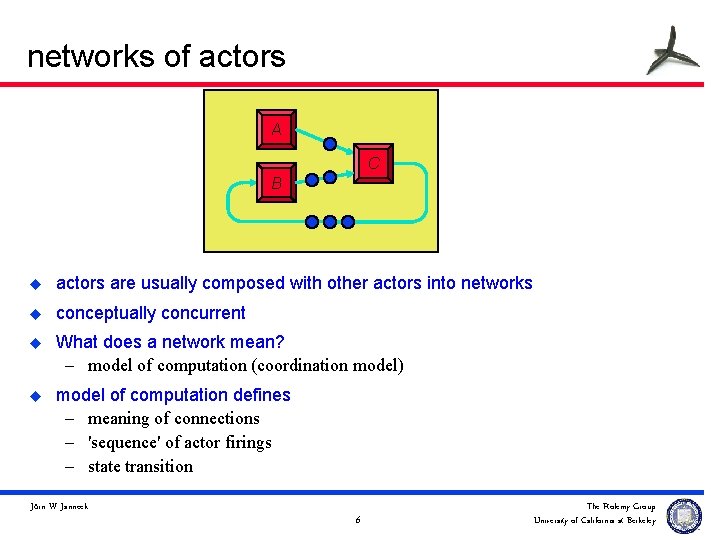
networks of actors A C B u actors are usually composed with other actors into networks u conceptually concurrent u What does a network mean? – model of computation (coordination model) u model of computation defines – meaning of connections – 'sequence' of actor firings – state transition Jörn W. Janneck 6 The Ptolemy Group University of California at Berkeley

actors and visual languages u actor networks are often represented using visual languages Þ actor models of computation natural match for (many) VL semantics Jörn W. Janneck 7 The Ptolemy Group University of California at Berkeley

specifying VL semantics 1. semantics of an actor • define an actor syntax first! • then describe what it means 2. semantics of an actor composition • again, syntax first • composition operator actors + network actor • Jörn W. Janneck the composition operator is the model of computation! 8 The Ptolemy Group University of California at Berkeley

semantics of actor compositions u the operational approach – describe a generic abstract machine – actors are 'machines' that interact with their generic environment – a special instance of that environment is a model of computation – examples: Ptolemy, Metropolis u two issues: – generic machine needs to anticipate the facilities needed by models of computation – actors become specific to models of computation Jörn W. Janneck 9 The Ptolemy Group University of California at Berkeley
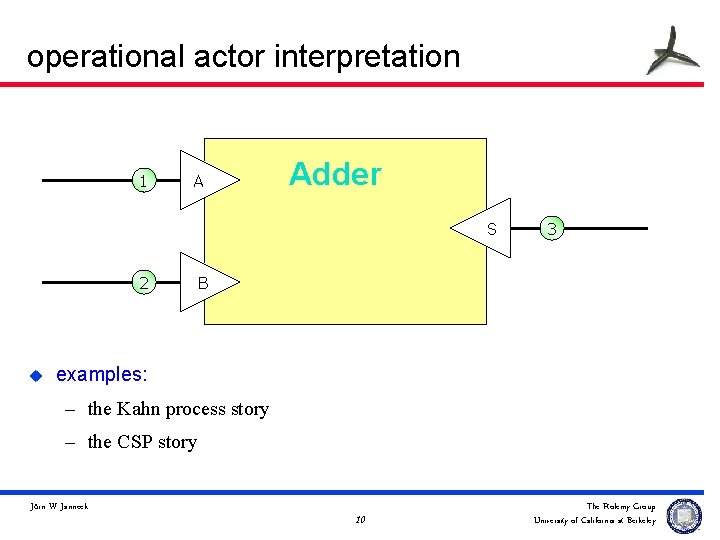
operational actor interpretation 1 A Adder S 2 u 3 B examples: – the Kahn process story – the CSP story Jörn W. Janneck 10 The Ptolemy Group University of California at Berkeley

semantics of actor composition actor Adder () Double A, Double B ==> Double S: action [a], [b] ==> [a + b] end u the language approach – consider an actor description a constraint on all possible behaviors u models of computation compose those descriptions – they may interpret an actor specification – thereby adding constraints to it, specializing it Jörn W. Janneck 11 The Ptolemy Group University of California at Berkeley

What is CAL? CAL is a (textual) language for writing actors. u supports a variety of platforms and models of computation – by supporting a variety of interpretations – by proserving lots of static structure in the actor description » token rates » dependencies u designed as a domain-specific language – it is intentionally incomplete u part of the Ptolemy project Jörn W. Janneck 12 The Ptolemy Group University of California at Berkeley

a simple example actor A (Double k) Double Input 1, Double Input 2 ==> Double Output: action [a], [b] ==> [k * (a + b)] end Jörn W. Janneck 13 The Ptolemy Group University of California at Berkeley

another example actor B () Double Input ==> Double Output: Integer n : = 0; Double sum : = 0; action [a] ==> [sum / n] do n : = n + 1; sum : = sum + a; end Jörn W. Janneck 14 The Ptolemy Group University of California at Berkeley

the CAL vision u provide flexible platform for expressing a wide range of actor functionality u generate (operational) implementations for specific platforms – Ptolemy/Java, C, Moses, . . . – bridge between modeling environments and implementation u serve as platform for composing actors – express models of computation as syntactic transformations in CAL – this makes models of computation portable to any CAL platform! u profiles for portability Jörn W. Janneck 15 The Ptolemy Group University of California at Berkeley

Some language features Jörn W. Janneck 16 The Ptolemy Group University of California at Berkeley
![multiple actions, action conditions actor C () Double Input ==> Double Output: action [a] multiple actions, action conditions actor C () Double Input ==> Double Output: action [a]](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-17.jpg)
multiple actions, action conditions actor C () Double Input ==> Double Output: action [a] ==> [a] guard a >= 0 end action [a] ==> [-a] guard a < 0 end actor D () Double Input ==> Double Output: action [a] ==> [abs(a)] end Jörn W. Janneck 17 The Ptolemy Group University of California at Berkeley
![nondeterminism actor E () Double Input ==> Double Output: action [a] ==> [a] end nondeterminism actor E () Double Input ==> Double Output: action [a] ==> [a] end](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-18.jpg)
nondeterminism actor E () Double Input ==> Double Output: action [a] ==> [a] end action [a] ==> [-a] end • • More than one action may be firable. Caltrop does not specify how this is resolved. It allows deterministic as well as non-deterministic implementations. Often, determinism can be ascertained statically. Jörn W. Janneck 18 The Ptolemy Group University of California at Berkeley
![port patterns actor Pairwise. Swap [T] () T Input ==> T Output: action [a, port patterns actor Pairwise. Swap [T] () T Input ==> T Output: action [a,](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-19.jpg)
port patterns actor Pairwise. Swap [T] () T Input ==> T Output: action [a, b] ==> [b, a] end u examples – [a, b, c] – [a, b, c | s] – [| s] Jörn W. Janneck 19 The Ptolemy Group University of California at Berkeley
![repeated patterns actor Reverse. Prefix [T] (Integer n) T Input ==> T Output: action repeated patterns actor Reverse. Prefix [T] (Integer n) T Input ==> T Output: action](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-20.jpg)
repeated patterns actor Reverse. Prefix [T] (Integer n) T Input ==> T Output: action [a] repeat n ==> [reverse(a)] repeat n end Jörn W. Janneck 20 The Ptolemy Group University of California at Berkeley
![multiports, channel selectors actor Switch [T] () multi T Data, Integer Select ==> T multiports, channel selectors actor Switch [T] () multi T Data, Integer Select ==> T](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-21.jpg)
multiports, channel selectors actor Switch [T] () multi T Data, Integer Select ==> T Output: action [a] i, [i] ==> [a] end Jörn W. Janneck 21 The Ptolemy Group University of California at Berkeley
![port tags actor Switch [T] () multi T Data, Integer Select ==> T Output: port tags actor Switch [T] () multi T Data, Integer Select ==> T Output:](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-22.jpg)
port tags actor Switch [T] () multi T Data, Integer Select ==> T Output: action Data: [a] i, Select: [i] ==> [a] end actor Switch [T] () multi T Data, Integer Select ==> T Output: action Select: [i], Data: [a] i ==> [a] end Jörn W. Janneck 22 The Ptolemy Group University of California at Berkeley
![action tags, action selectors actor Fair. Merge [T] () T Input 1, T Input action tags, action selectors actor Fair. Merge [T] () T Input 1, T Input](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-23.jpg)
action tags, action selectors actor Fair. Merge [T] () T Input 1, T Input 2 ==> T Output: A: action Input 1: [a] ==> [a] end B: action Input 2: [a] ==> [a] end selector (AB)* end other selectors are conceivable, e. g. • (AB)* | (BA)* • ( (AB) | (BA) )* Jörn W. Janneck 23 The Ptolemy Group University of California at Berkeley
![action conditions, state actor Fair. Merge [T] () T Input 1, T Input 2 action conditions, state actor Fair. Merge [T] () T Input 1, T Input 2](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-24.jpg)
action conditions, state actor Fair. Merge [T] () T Input 1, T Input 2 ==> T Output: Integer s : = 1; action Input 1: [a] ==> [a] guard s = 1 do s : = 2; end action Input 2: [a] ==> [a] guard s = 2 do s : = 1; end Jörn W. Janneck 24 The Ptolemy Group University of California at Berkeley
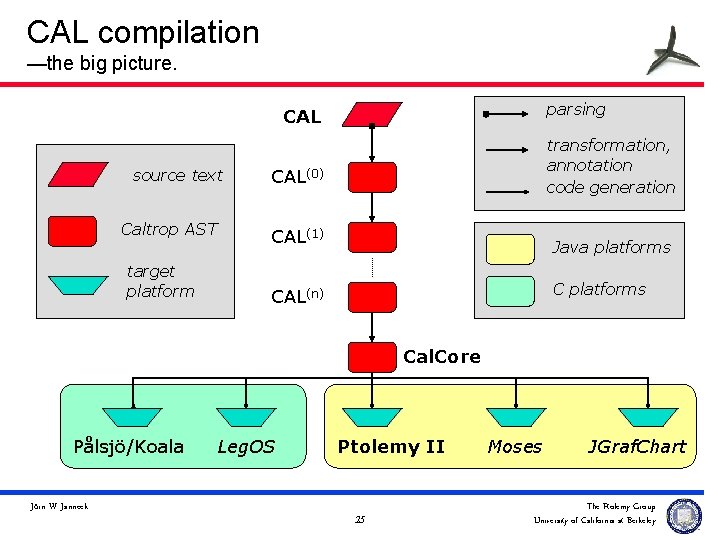
CAL compilation —the big picture. parsing CAL source text Caltrop AST target platform transformation, annotation code generation CAL(0) CAL(1) Java platforms CAL(n) Cal. Core Pålsjö/Koala Jörn W. Janneck Leg. OS Ptolemy II 25 Moses JGraf. Chart The Ptolemy Group University of California at Berkeley
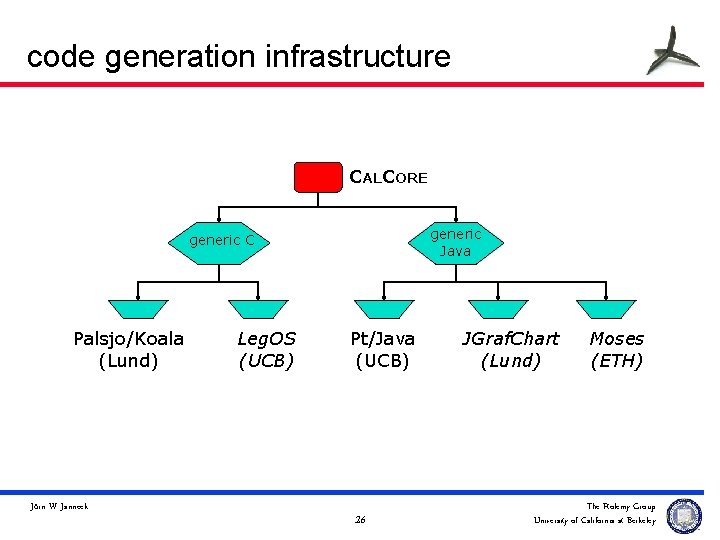
code generation infrastructure CALCORE generic Java generic C Palsjo/Koala (Lund) Jörn W. Janneck Leg. OS (UCB) Pt/Java (UCB) 26 JGraf. Chart (Lund) Moses (ETH) The Ptolemy Group University of California at Berkeley
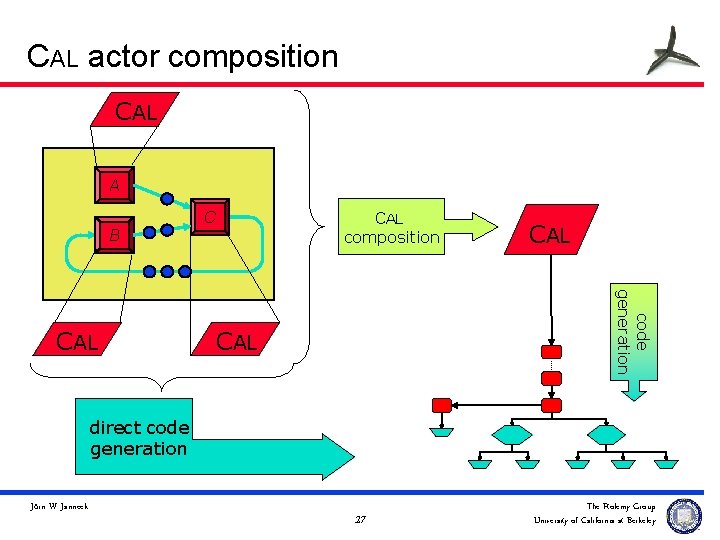
CAL actor composition CAL A CAL composition C B code generation CAL CAL direct code generation Jörn W. Janneck 27 The Ptolemy Group University of California at Berkeley

project status u We have. . . – the language definition » including an informal semantics – Java code generator » generic + Ptolemy » usable, but not complete » ongoing work on porting Ptolemy actor library – C code generator » » generic + Palsjo usable, but not complete Lund University uses it for writing control software for robot Swedish company wants to use the language for writing DSP applications – some work on static scheduling of actor networks – some work on actor composition Jörn W. Janneck 28 The Ptolemy Group University of California at Berkeley

project status u We would like. . . – formal actor semantics – composition and composition language – more extensive code generation » » more complete more platforms more languages larger function libraries – larger actor libraries u . . . but most of all. . . Collaborators! Jörn W. Janneck 29 The Ptolemy Group University of California at Berkeley

Thanks. www. gigascale. org/caltrop Jörn W. Janneck 30 The Ptolemy Group University of California at Berkeley
Jörn W. Janneck 31 The Ptolemy Group University of California at Berkeley

Motivation Writing simple actors should be simple. u But: The Ptolemy API is very rich, and writing actors in it requires considerable skill. u However: Many Ptolemy actors have considerable commonalities - they are written in a stylized format. Jörn W. Janneck 32 The Ptolemy Group University of California at Berkeley

Motivation We should generate many actors from a more abstract description. u Benefits: – reduces amount of code to be written – makes writing actors more accessible – reduces error probability – makes code more versatile » actors may be retargeted to other platforms, or new versions of the Ptolemy API Jörn W. Janneck 33 The Ptolemy Group University of California at Berkeley

Overview of the implementation general architecture aspects of the Pt/Java implementation Jörn W. Janneck 34 The Ptolemy Group University of California at Berkeley
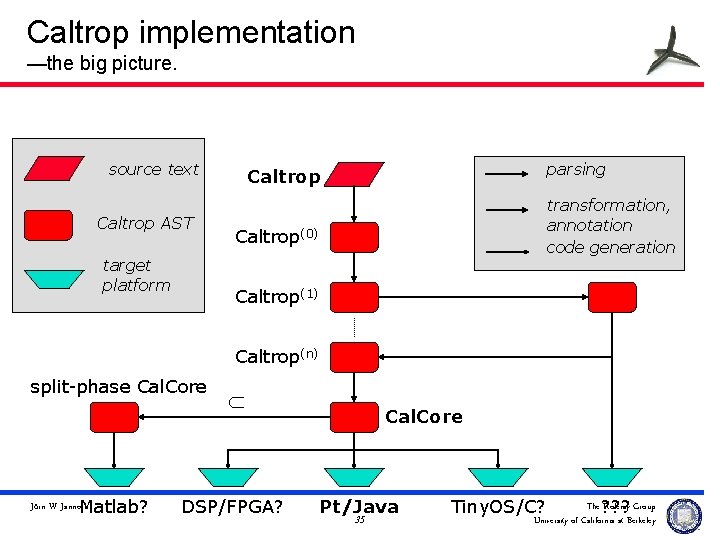
Caltrop implementation —the big picture. source text Caltrop AST target platform parsing Caltrop transformation, annotation code generation Caltrop(0) Caltrop(1) Caltrop(n) split-phase Cal. Core Jörn W. Janneck Matlab? Ì DSP/FPGA? Cal. Core Pt/Java 35 Tiny. OS/C? The ? ? ? Ptolemy Group University of California at Berkeley

Caltrop implementation u many small modules – transformers, annotaters, checkers u transforming Caltrop into some language subset u Cal. Core – small, semantically complete subset – minimal language for code generation, analysis, transformation – built on functional and procedural closures Jörn W. Janneck 36 The Ptolemy Group University of California at Berkeley

Transformers & annotators u replace control structures u replace port patterns u sort variable declarations u replace operators u propagate type information u check static properties u tag port patterns u . . . Jörn W. Janneck 37 The Ptolemy Group University of California at Berkeley

Caltrop implementation u Benefits: – Much of the ‘hard’ stuff can be done on the same data structure, exploiting the regularities of the Caltrop/Cal. Core semantics and the existing software infrastructure. – Code generators becomes relatively small, thus making retargeting easier. – Intermediate results are valid Caltrop programs, making debugging a lot easier. » We can look at them easily. » We can use the parser and the well-formedness/type checkers themselves as debugging tools! Jörn W. Janneck 38 The Ptolemy Group University of California at Berkeley
![Switch in Cal. Core* actor Switch [T] () multi T Data, Integer Select ==> Switch in Cal. Core* actor Switch [T] () multi T Data, Integer Select ==>](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-39.jpg)
Switch in Cal. Core* actor Switch [T] () multi T Data, Integer Select ==> T Output : action Select: : [|G 0], Data: : [|G 2] all ==> Output: : [a] where G 1, G 3 with Boolean G 1 : = available(G 0, 1), Integer i : = if G 1 then G 0[0] else null end, Integer G 4 : = i, Boolean G 3 : = available(G 2[G 4], 1), Integer a : = if G 3 then G 2[G 4][0] else null end end *Actually, we are cheating here; Cal. Core is in fact even Jörn W. Janneck primitive. And even less readable. . . The Ptolemy Group more 39 University of California at Berkeley

Cal. Core ==> Pt/Java u different programming models – single atomic action vs prefire/firen/postfire – referentially transparent access to channels vs. token consuming read methods – stateful computation vs state-invariant fire Jörn W. Janneck 40 The Ptolemy Group University of California at Berkeley
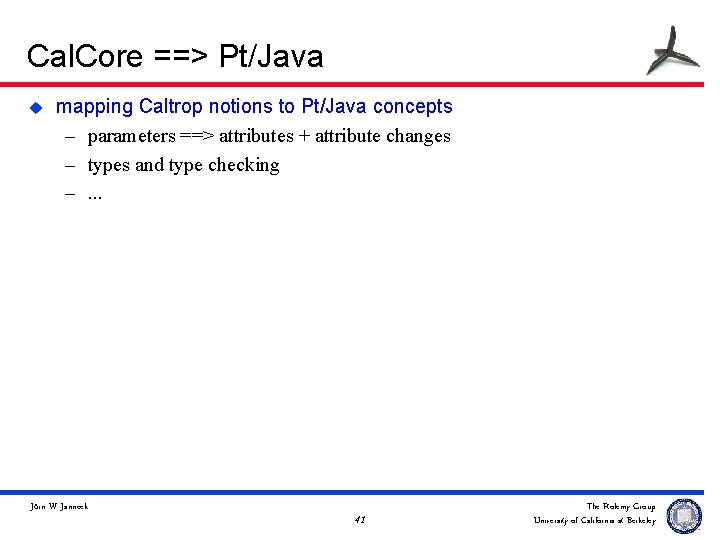
Cal. Core ==> Pt/Java u mapping Caltrop notions to Pt/Java concepts – parameters ==> attributes + attribute changes – types and type checking –. . . Jörn W. Janneck 41 The Ptolemy Group University of California at Berkeley
![What goes into prefire()? actor Switch [T] () multi T Data, Integer Select ==> What goes into prefire()? actor Switch [T] () multi T Data, Integer Select ==>](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-42.jpg)
What goes into prefire()? actor Switch [T] () multi T Data, Integer Select ==> T Output : action Select: : [|G 0], Data: : [|G 2] all ==> Output: : [a] where G 1, G 3 with Boolean G 1 : = available(G 0, 1), Integer i : = if G 1 then G 0[0] else null end, Integer G 4 : = i, Boolean G 3 : = available(G 2[G 4], 1), Integer a : = if G 3 then G 2[G 4][0] else null end end All computation that is required in order to decide firability? Just the part of it before the first token access? Jörn W. Janneck 42 The Ptolemy Group University of California at Berkeley

prefire/fire u aggressive vs defensive condition evaluation u incrementally computing conditions u reusing computation done in prefire u Should tokens read in prefire be kept if prefire returns false? Jörn W. Janneck 43 The Ptolemy Group University of California at Berkeley
![fire/postfire action Input 1: : [a] ==> [a] where s = 1 : s fire/postfire action Input 1: : [a] ==> [a] where s = 1 : s](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-44.jpg)
fire/postfire action Input 1: : [a] ==> [a] where s = 1 : s : = 2; end prefire postfire action Input 1: : [|G 0] ==> Output: : [a] where equals(s, 1), G 1 with Boolean G 1 : = available(G 0, 1), T a : = if G 1 then G 0[0] else null end : s : = 2; end Computation that does not affect the output Jörn W. Janneck be done in postfire. The Ptolemy Group can University of California at Berkeley 44

State management If state needs to be changed in order to compute output, it needs to be shadowed. u safe state management – referentially transparent expressions – no aliasing of stateful structures Jörn W. Janneck 45 The Ptolemy Group University of California at Berkeley

State management actor B () Double Input ==> Double Output: Integer n : = 0; Double sum : = 0; action [a] ==> [sum / n] : n : = n + 1; sum : = sum + a; end The division between fire and postfire can be expressed in Caltrop (btw, this is a non-Cal. Core transformation) using action tags and selectors. Jörn W. Janneck The Ptolemy Group 46 University of California at Berkeley

State management actor B () Double Input ==> Double Output: Integer n : = 0; Integer n$shadow; Double sum : = 0; Double sum$shadow; fire: action [a] ==> [sum$shadow / n$shadow] : n$shadow : = n; sum$shadow : = sum; n$shadow : = n$shadow + 1; sum$shadow : = sum$shadow + a; end postfire: action ==> : n : = n$shadow; sum : = sum$shadow; end selector (fire+ postfire)* end Jörn W. Janneck 47 The Ptolemy Group University of California at Berkeley

Things we need to do. . . Jörn W. Janneck 48 The Ptolemy Group University of California at Berkeley

Short term “grunt” work u well-formedness checks u type system, type checking u split-phase analyses u interpreter (+ wrapper for Pt/Java) u optimizations, big and small u other transformers, annotators Jörn W. Janneck 49 The Ptolemy Group University of California at Berkeley

Fun mid-term projects u static analysis of actor properties (data rates, dependency on state, parameters, input, . . . ) u relation to Mo. C (e. g. BDF) u computing interface automata from actor descriptions u code generators to other platforms and languages u code generation for composite actors? Jörn W. Janneck 50 The Ptolemy Group University of California at Berkeley

Even funner long-term projects u generic code generation framework – maybe based on Calif? u extending the language – higher-order constructs – domains/directors+receivers u a formal semantics, a framework for actor analysis Jörn W. Janneck 51 The Ptolemy Group University of California at Berkeley

Caltrop resources www. gigascale. org/caltrop Meeting: Tuesdays, 1: 30 pm, DOP Center Library (We need Caltroopers!) Jörn W. Janneck 52 The Ptolemy Group University of California at Berkeley

Other slides Jörn W. Janneck 53 The Ptolemy Group University of California at Berkeley

What is CAL? CAL is a textual syntax for representing dataflow actors. u formal semantics u easily retargetable to different tools and environments Jörn W. Janneck 54 The Ptolemy Group University of California at Berkeley

What can we do with CAL? We can formally manipulate actor descriptions. u actor transformation u code generation – to Java, C u actor composition Jörn W. Janneck 55 The Ptolemy Group University of California at Berkeley
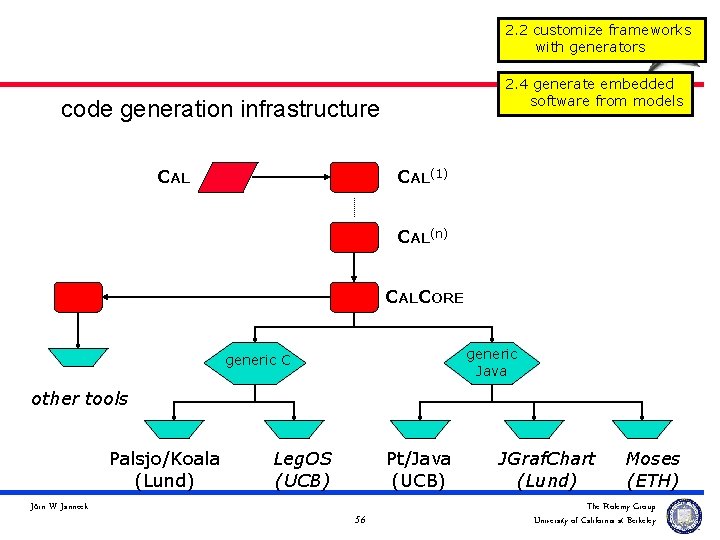
2. 2 customize frameworks with generators 2. 4 generate embedded software from models code generation infrastructure CAL(1) CAL(n) CALCORE generic Java generic C other tools Palsjo/Koala (Lund) Jörn W. Janneck Leg. OS (UCB) Pt/Java (UCB) 56 JGraf. Chart (Lund) Moses (ETH) The Ptolemy Group University of California at Berkeley

CAL snippets Jörn W. Janneck 57 The Ptolemy Group University of California at Berkeley

Can you guess what this does? actor A (Double k) Double Input 1, Double Input 2 ==> Double Output: action [a], [b] ==> [k*(a + b)] end Jörn W. Janneck 58 The Ptolemy Group University of California at Berkeley

Or this? actor B () Double Input ==> Double Output: Integer n : = 0; Double sum : = 0; action [a] ==> [sum / n] : n : = n + 1; sum : = sum + a; end Jörn W. Janneck 59 The Ptolemy Group University of California at Berkeley
![Multiple actions, action conditions actor C () Double Input ==> Double Output: action [a] Multiple actions, action conditions actor C () Double Input ==> Double Output: action [a]](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-60.jpg)
Multiple actions, action conditions actor C () Double Input ==> Double Output: action [a] ==> [a] where a >= 0 end action [a] ==> [-a] where a < 0 end actor D () Double Input ==> Double Output: action [a] ==> [abs(a)] end Jörn W. Janneck 60 The Ptolemy Group University of California at Berkeley
![Nondeterminism actor E () Double Input ==> Double Output: action [a] ==> [a] end Nondeterminism actor E () Double Input ==> Double Output: action [a] ==> [a] end](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-61.jpg)
Nondeterminism actor E () Double Input ==> Double Output: action [a] ==> [a] end action [a] ==> [-a] end • More than one action may be firable. • Caltrop does not specify how this is resolved. • It allows deterministic as well as nondeterministic implementations. • Often, determinism can be ascertained Jörn W. Janneck statically. The Ptolemy Group 61 University of California at Berkeley
![Port patterns actor Pairwise. Swap [T] () T Input ==> T Output: action [a, Port patterns actor Pairwise. Swap [T] () T Input ==> T Output: action [a,](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-62.jpg)
Port patterns actor Pairwise. Swap [T] () T Input ==> T Output: action [a, b] ==> [b, a] end u examples – [a, b, c] – [a, b, c | s] – [| s] Jörn W. Janneck 62 The Ptolemy Group University of California at Berkeley
![Repeated patterns actor Reverse. Prefix [T] (Integer n) T Input ==> T Output: action Repeated patterns actor Reverse. Prefix [T] (Integer n) T Input ==> T Output: action](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-63.jpg)
Repeated patterns actor Reverse. Prefix [T] (Integer n) T Input ==> T Output: action [a] repeat n ==> [reverse(a)] repeat n end Jörn W. Janneck 63 The Ptolemy Group University of California at Berkeley
![Channel selectors actor Switch [T] () multi T Data, Integer Select ==> T Output: Channel selectors actor Switch [T] () multi T Data, Integer Select ==> T Output:](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-64.jpg)
Channel selectors actor Switch [T] () multi T Data, Integer Select ==> T Output: action [a] i, [i] ==> [a] end Jörn W. Janneck 64 The Ptolemy Group University of California at Berkeley
![Action tags, action selectors actor Fair. Merge [T] () T Input 1, T Input Action tags, action selectors actor Fair. Merge [T] () T Input 1, T Input](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-65.jpg)
Action tags, action selectors actor Fair. Merge [T] () T Input 1, T Input 2 ==> T Output: A: action Input 1: : [a] ==> [a] end B: action Input 2: : [a] ==> [a] end selector (AB)* end Jörn W. Janneck other selectors are conceivable, e. g. • (AB)* | (BA)* • ( (AB) | (BA) )* 65 The Ptolemy Group University of California at Berkeley
![Action conditions, state actor Fair. Merge [T] () T Input 1, T Input 2 Action conditions, state actor Fair. Merge [T] () T Input 1, T Input 2](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-66.jpg)
Action conditions, state actor Fair. Merge [T] () T Input 1, T Input 2 ==> T Output: Integer s : = 1; action Input 1: : [a] ==> [a] where s = 1: s : = 2; end action Input 2: : [a] ==> [a] where s = 2: s : = 1; end Jörn W. Janneck 66 The Ptolemy Group University of California at Berkeley

Motivation Writing simple actors should be simple. u But: The Ptolemy API is very rich, and writing actors in it requires considerable skill. u However: Many Ptolemy actors have considerable commonalities - they are written in a stylized format. Jörn W. Janneck 67 The Ptolemy Group University of California at Berkeley

Motivation We should generate many actors from a more abstract description. u Benefits: – reduces amount of code to be written – makes writing actors more accessible – reduces error probability – makes code more versatile » actors may be retargeted to other platforms, or new versions of the Ptolemy API Jörn W. Janneck 68 The Ptolemy Group University of California at Berkeley

Why is Caltrop useful for me? u For Ptolemy users: – Makes it easier to write atomic actors. – Makes Ptolemy accessible to a wider audience. u For Ptolemy ‘hackers’: – Reduces possibilities for bugs. – Makes actors more reusable. – Enables analysis and efficient code generation. Jörn W. Janneck 69 The Ptolemy Group University of California at Berkeley

Transformers & annotators u replace control structures u replace port patterns u sort variable declarations u replace operators u propagate type information u check static properties u tag port patterns u . . . Jörn W. Janneck 70 The Ptolemy Group University of California at Berkeley

CAL implementation u highly modular – transformers, annotaters, checkers u transforming Cal into some language subset u Cal. Core – small, semantically complete subset – minimal language for code generation, analysis, transformation – built on functional and procedural closures Jörn W. Janneck 71 The Ptolemy Group University of California at Berkeley

CAL implementation u Benefits: – Much of the ‘hard’ stuff can be done on the same data structure, exploiting the regularities of the Caltrop/Cal. Core semantics and the existing software infrastructure. – Code generators becomes relatively small, thus making retargeting easier. – Intermediate results are valid Caltrop programs, making debugging a lot easier. » We can look at them easily. » We can use the parser and the well-formedness/type checkers themselves as debugging tools! Jörn W. Janneck 72 The Ptolemy Group University of California at Berkeley
![Port tags actor Switch [T] () multi T Data, Integer Select ==> T Output: Port tags actor Switch [T] () multi T Data, Integer Select ==> T Output:](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-73.jpg)
Port tags actor Switch [T] () multi T Data, Integer Select ==> T Output: action Data: : [a] i, Select: : [i] ==> [a] end actor Switch [T] () multi T Data, Integer Select ==> T Output: action Select: : [i], Data: : [a] i ==> [a] end Jörn W. Janneck 73 The Ptolemy Group University of California at Berkeley

Overview of the implementation general architecture aspects of the Pt/Java implementation Jörn W. Janneck 74 The Ptolemy Group University of California at Berkeley
![Switch in Cal. Core* actor Switch [T] () multi T Data, Integer Select ==> Switch in Cal. Core* actor Switch [T] () multi T Data, Integer Select ==>](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-75.jpg)
Switch in Cal. Core* actor Switch [T] () multi T Data, Integer Select ==> T Output : action Select: : [|G 0], Data: : [|G 2] all ==> Output: : [a] where G 1, G 3 with Boolean G 1 : = available(G 0, 1), Integer i : = if G 1 then G 0[0] else null end, Integer G 4 : = i, Boolean G 3 : = available(G 2[G 4], 1), Integer a : = if G 3 then G 2[G 4][0] else null end end *Actually, we are cheating here; Cal. Core is in fact even Jörn W. Janneck primitive. And even less readable. . . The Ptolemy Group more 75 University of California at Berkeley

Cal. Core ==> Pt/Java u different programming models – single atomic action vs prefire/firen/postfire – referentially transparent access to channels vs. token consuming read methods – stateful computation vs state-invariant fire Jörn W. Janneck 76 The Ptolemy Group University of California at Berkeley
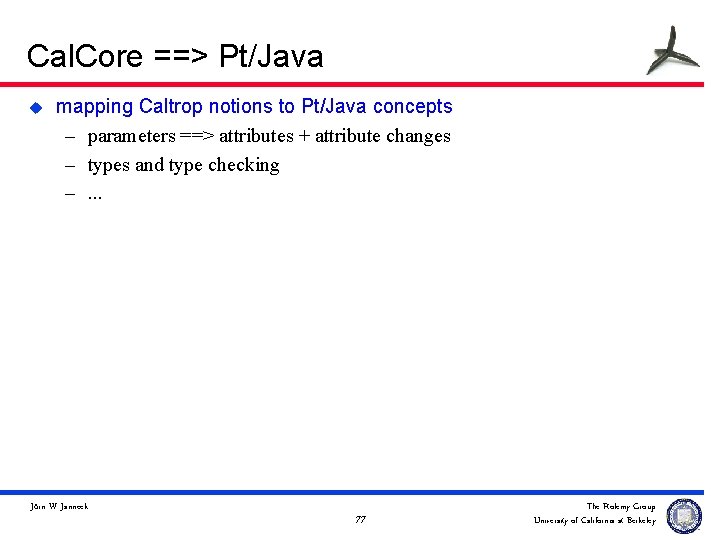
Cal. Core ==> Pt/Java u mapping Caltrop notions to Pt/Java concepts – parameters ==> attributes + attribute changes – types and type checking –. . . Jörn W. Janneck 77 The Ptolemy Group University of California at Berkeley
![What goes into prefire()? actor Switch [T] () multi T Data, Integer Select ==> What goes into prefire()? actor Switch [T] () multi T Data, Integer Select ==>](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-78.jpg)
What goes into prefire()? actor Switch [T] () multi T Data, Integer Select ==> T Output : action Select: : [|G 0], Data: : [|G 2] all ==> Output: : [a] where G 1, G 3 with Boolean G 1 : = available(G 0, 1), Integer i : = if G 1 then G 0[0] else null end, Integer G 4 : = i, Boolean G 3 : = available(G 2[G 4], 1), Integer a : = if G 3 then G 2[G 4][0] else null end end All computation that is required in order to decide firability? Just the part of it before the first token access? Jörn W. Janneck 78 The Ptolemy Group University of California at Berkeley

prefire/fire u aggressive vs defensive condition evaluation u incrementally computing conditions u reusing computation done in prefire u Should tokens read in prefire be kept if prefire returns false? Jörn W. Janneck 79 The Ptolemy Group University of California at Berkeley
![fire/postfire action Input 1: : [a] ==> [a] where s = 1 : s fire/postfire action Input 1: : [a] ==> [a] where s = 1 : s](http://slidetodoc.com/presentation_image_h/0eb7533257ad7c1f68ecd10d63cf01a3/image-80.jpg)
fire/postfire action Input 1: : [a] ==> [a] where s = 1 : s : = 2; end prefire postfire action Input 1: : [|G 0] ==> Output: : [a] where equals(s, 1), G 1 with Boolean G 1 : = available(G 0, 1), T a : = if G 1 then G 0[0] else null end : s : = 2; end Computation that does not affect the output Jörn W. Janneck be done in postfire. The Ptolemy Group can University of California at Berkeley 80

State management If state needs to be changed in order to compute output, it needs to be shadowed. u safe state management – referentially transparent expressions – no aliasing of stateful structures Jörn W. Janneck 81 The Ptolemy Group University of California at Berkeley

State management actor B () Double Input ==> Double Output: Integer n : = 0; Double sum : = 0; action [a] ==> [sum / n] : n : = n + 1; sum : = sum + a; end The division between fire and postfire can be expressed in Caltrop (btw, this is a non-Cal. Core transformation) using action tags and selectors. Jörn W. Janneck The Ptolemy Group 82 University of California at Berkeley

State management actor B () Double Input ==> Double Output: Integer n : = 0; Integer n$shadow; Double sum : = 0; Double sum$shadow; fire: action [a] ==> [sum$shadow / n$shadow] : n$shadow : = n; sum$shadow : = sum; n$shadow : = n$shadow + 1; sum$shadow : = sum$shadow + a; end postfire: action ==> : n : = n$shadow; sum : = sum$shadow; end selector (fire+ postfire)* end Jörn W. Janneck 83 The Ptolemy Group University of California at Berkeley

Things we need to do. . . Jörn W. Janneck 84 The Ptolemy Group University of California at Berkeley

Short term “grunt” work u well-formedness checks u type system, type checking u split-phase analyses u interpreter (+ wrapper for Pt/Java) u optimizations, big and small u other transformers, annotators Jörn W. Janneck 85 The Ptolemy Group University of California at Berkeley

Fun mid-term projects u static analysis of actor properties (data rates, dependency on state, parameters, input, . . . ) u relation to Mo. C (e. g. BDF) u computing interface automata from actor descriptions u code generators to other platforms and languages u code generation for composite actors? Jörn W. Janneck 86 The Ptolemy Group University of California at Berkeley

Even funner long-term projects u generic code generation framework – maybe based on Calif? u extending the language – higher-order constructs – domains/directors+receivers u a formal semantics, a framework for actor analysis Jörn W. Janneck 87 The Ptolemy Group University of California at Berkeley

Caltrop resources www. gigascale. org/caltrop Meeting: Tuesdays, 1: 30 pm, DOP Center Library (We need Caltroopers!) Jörn W. Janneck 88 The Ptolemy Group University of California at Berkeley
- Slides: 88