5 TwoDimensional Geometric Transformations Contents o o o

5 Two-Dimensional Geometric Transformations

Contents o o o Preliminary Basic transformations Homogeneous coordinate System Composite transformations Reflection and Shearing Transformations between coordinate systems Geometric Transformation

Geometric Transformation o Geometric Transformation v 물체의 좌표를 바꾸는 것 v Translation, Rotation, Scaling o Motivation - Why do we need transformations in computer graphics? v As a viewing aid v As a modeling tool v As an image manipulation tool Geometric Transformation

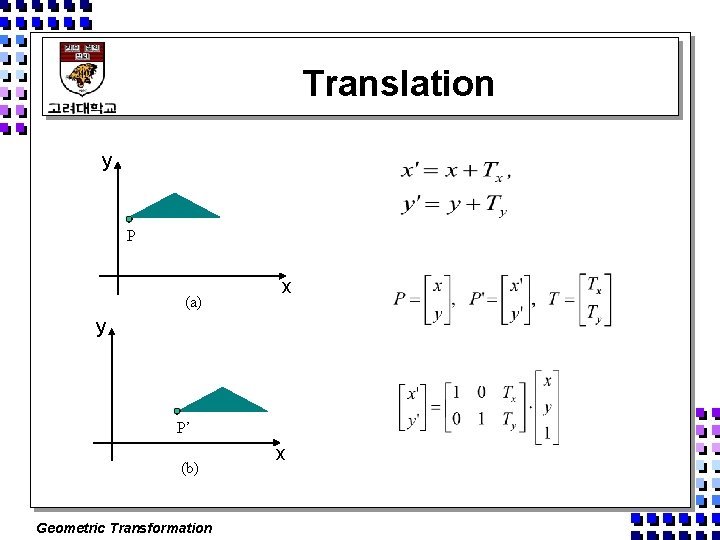
Translation y P (a) x y P’ (b) Geometric Transformation x

Homogeneous Coordinates In basic Transformations, ( Addition ) Only Translation is treated differently ( Multiplication ) How can we represent the composite transformaiton into a single matrix? M Geometric Transformation

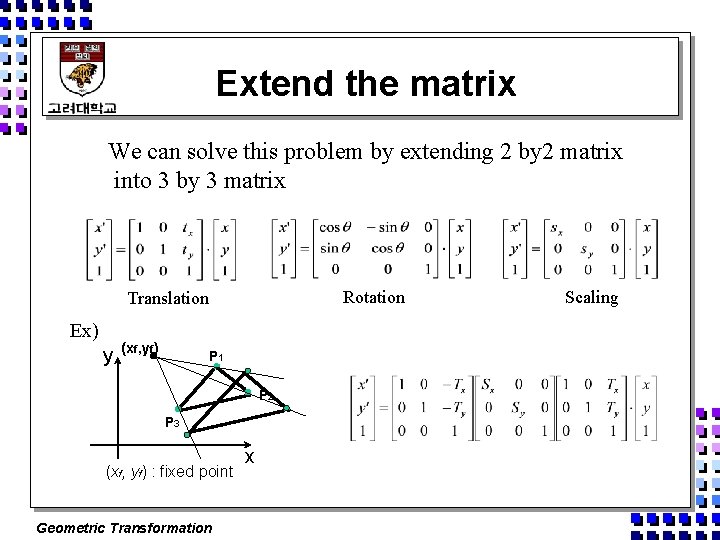
Extend the matrix We can solve this problem by extending 2 by 2 matrix into 3 by 3 matrix Rotation Translation Ex) y (xf, yf) P 1 P 2 P 3 (xf, yf) : fixed point Geometric Transformation x Scaling

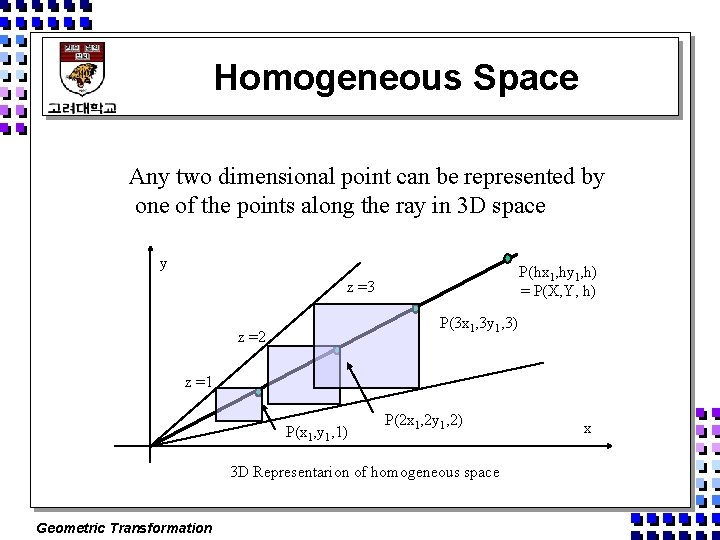
Homogeneous Space Any two dimensional point can be represented by one of the points along the ray in 3 D space y P(hx 1, hy 1, h) = P(X, Y, h) z =3 P(3 x 1, 3 y 1, 3) z =2 z =1 P(x 1, y 1, 1) P(2 x 1, 2 y 1, 2) 3 D Representarion of homogeneous space Geometric Transformation x

Point at Infinity The points with h=0 are called points at infinity, and this will not appear very often. Ex) [ X Y h ] = [ 4 3 1] Geometric Transformation

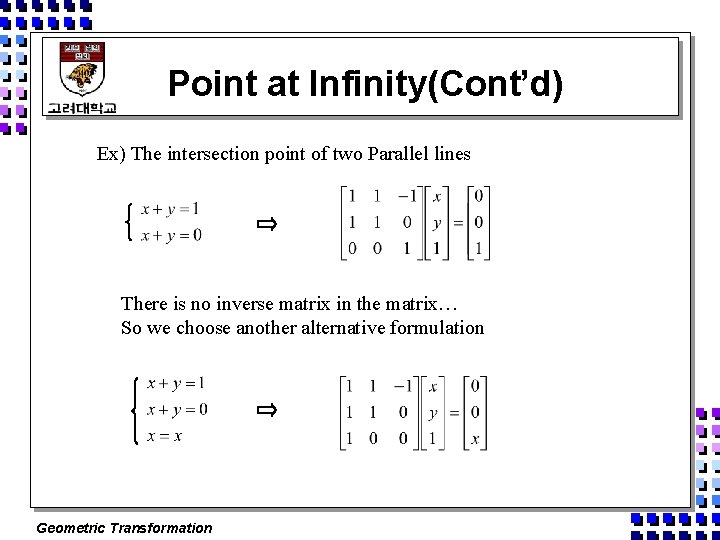
Point at Infinity(Cont’d) Ex) The intersection point of two Parallel lines There is no inverse matrix in the matrix… So we choose another alternative formulation Geometric Transformation

Point at Infinity(Cont’d) The resulting homogeneous coordinates [1 -1 0] represent the ‘point of intersection’ for the two parallel lines, i. e. a point at infinity. Geometric Transformation

Why Homogeneous? B A Two Lines are intersect each other if they are not parallel Non-Homogeneous treatment !! Geometric Transformation

General 2 D Transformation Matrix Rotation Scaling Translation Perspective transformation Where, Geometric Transformation

Composite Transformation Matrix Geometric Transformation

Composite Transformation o 연속적인 두 번 평행이동 (5 -23) P’ = T(tx 2, ty 2) · {T (tx 1, ty 1)·P} = {T(tx 2, ty 2) · T (tx 1, ty 1)} · P (5 -24) (5 -25) T(tx 2, ty 2) · T (tx 1, ty 1) = T(tx 1 + tx 2, ty 1 + ty 2) o 연속적인 두 번 회전 (5 -26) P’ = R( 2) · {R( 1) · P} = {R( 2) · R( 1)} · P (5 -27) R( 2) ·R( 1) = R( 2+ 1) (5 -28) P’ = R( 2+ 1) · P Geometric Transformation

Composite Transformation (계속) o 연속적인 두 번 신축 (5 -29) (5 -30) S(sx 2, sy 2) · S (sx 1, sy 1) = S(sx 1· sx 2, sy 1 · sy 2) Geometric Transformation

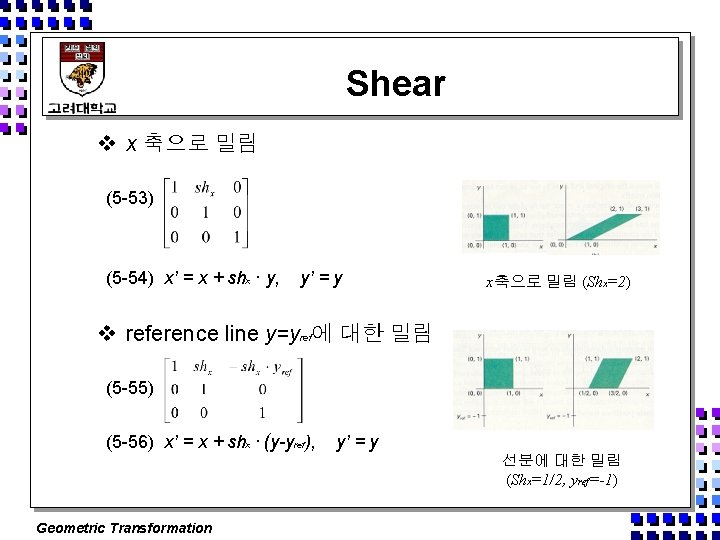
Shear v x 축으로 밀림 (5 -53) (5 -54) x’ = x + shx · y, y’ = y x축으로 밀림 (Shx=2) v reference line y=yref에 대한 밀림 (5 -55) (5 -56) x’ = x + shx · (y-yref), y’ = y 선분에 대한 밀림 (Shx=1/2, yref=-1) Geometric Transformation

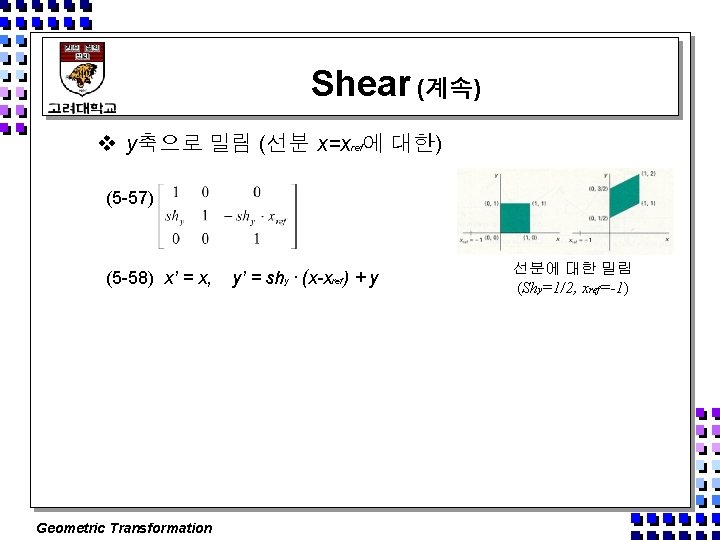
Shear (계속) v y축으로 밀림 (선분 x=xref에 대한) (5 -57) (5 -58) x’ = x, Geometric Transformation y’ = shy · (x-xref) + y 선분에 대한 밀림 (Shy=1/2, xref=-1)

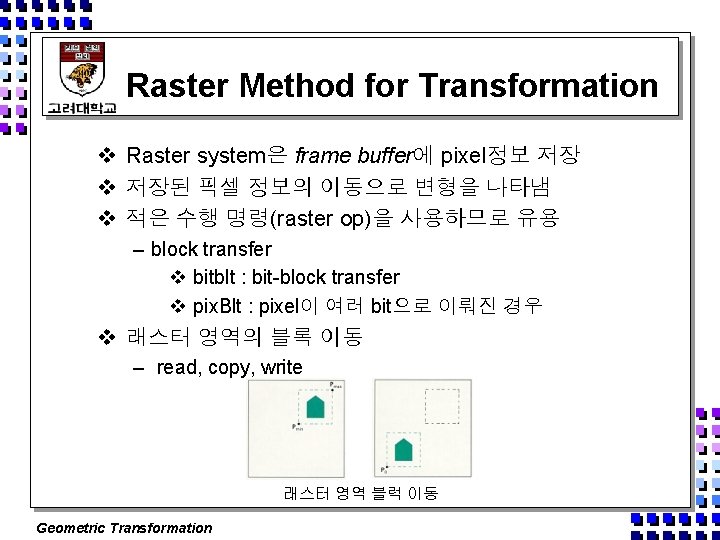
Raster Method for Transformation v Raster system은 frame buffer에 pixel정보 저장 v 저장된 픽셀 정보의 이동으로 변형을 나타냄 v 적은 수행 명령(raster op)을 사용하므로 유용 – block transfer v bitblt : bit-block transfer v pix. Blt : pixel이 여러 bit으로 이뤄진 경우 v 래스터 영역의 블록 이동 – read, copy, write 래스터 영역 블럭 이동 Geometric Transformation