Geometric Transformations General Transformations n A transformation maps























![Idle and Mouse callbacks void spin. Cube() { theta[axis] += 2. 0; if( theta[axis] Idle and Mouse callbacks void spin. Cube() { theta[axis] += 2. 0; if( theta[axis]](https://slidetodoc.com/presentation_image_h2/52785e4be79baa5d65501c0bc7f79a58/image-33.jpg)
![Display callback void display() { gl. Clear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); gl. Load. Identity(); gl. Rotatef(theta[0], Display callback void display() { gl. Clear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); gl. Load. Identity(); gl. Rotatef(theta[0],](https://slidetodoc.com/presentation_image_h2/52785e4be79baa5d65501c0bc7f79a58/image-34.jpg)




- Slides: 38

Geometric Transformations

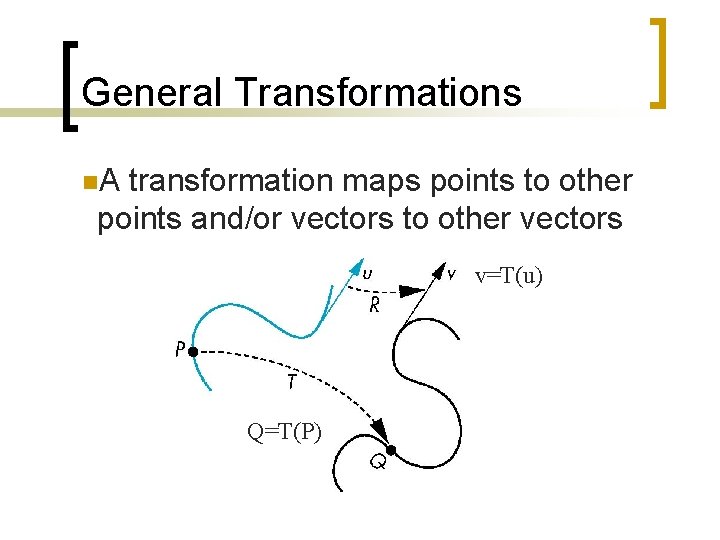
General Transformations n. A transformation maps points to other points and/or vectors to other vectors v=T(u) Q=T(P)

Affine Transformations n. Line preserving n. Characteristic of many physically important transformations ¡ Rigid body transformations: rotation, translation ¡ Scaling, shear n. Importance in graphics is that we need only transform endpoints of line segments and let implementation draw line segment between the transformed endpoints

Notation We will be working with both coordinate-free representations of transformations and representations within a particular frame P, Q, R: points in an affine space u, v, w: vectors in an affine space a, b, g: scalars p, q, r: representations of points -array of 4 scalars in homogeneous coordinates u, v, w: representations of points -array of 4 scalars in homogeneous coordinates

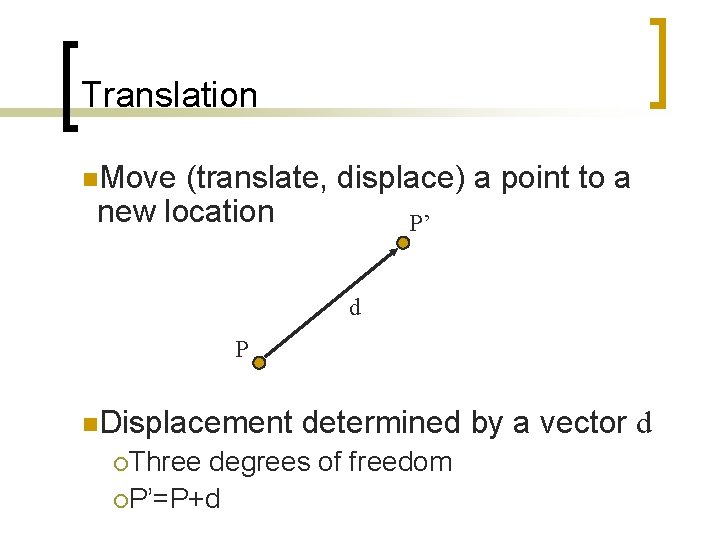
Translation n. Move (translate, displace) a point to a new location P’ d P n. Displacement ¡Three determined by a vector d degrees of freedom ¡P’=P+d

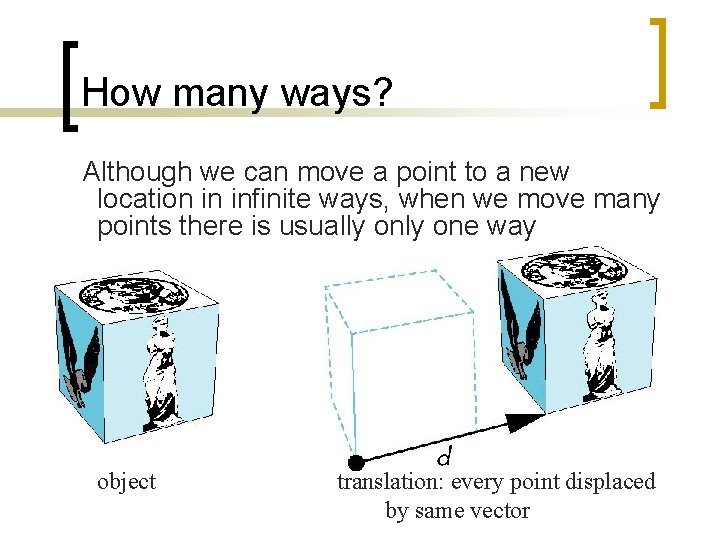
How many ways? Although we can move a point to a new location in infinite ways, when we move many points there is usually one way object translation: every point displaced by same vector

Translation Using Representations Using the homogeneous coordinate representation in some frame p=[ x y z 1]T p’=[x’ y’ z’ 1]T d=[dx dy dz 0]T note that this expression is in Hence p’ = p + d or four dimensions and expresses x’=x+dx that point = vector + point y’=y+dy z’=z+dz

Translation Matrix We can also express translation using a 4 x 4 matrix T in homogeneous coordinates p’=Tp where T = T(dx, dy, dz) = This form is better for implementation because all affine transformations can be expressed this way and multiple transformations can be concatenated together

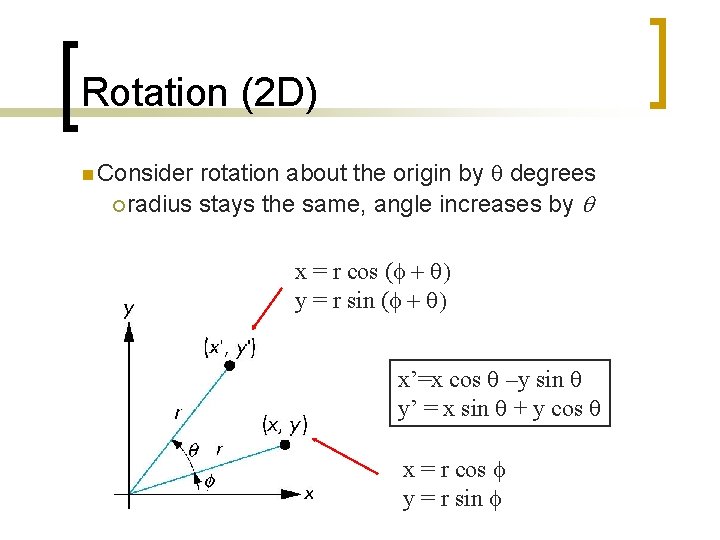
Rotation (2 D) rotation about the origin by q degrees ¡ radius stays the same, angle increases by q n Consider x = r cos (f + q) y = r sin (f + q) x’=x cos q –y sin q y’ = x sin q + y cos q x = r cos f y = r sin f

Rotation about the z axis n. Rotation about z axis in three dimensions leaves all points with the same z ¡Equivalent to rotation in two dimensions in planes of constant z x’=x cos q –y sin q y’ = x sin q + y cos q z’ =z ¡or in homogeneous coordinates p’=Rz(q)p

Rotation Matrix R = Rz(q) =

Rotation about x and y axes n Same argument as for rotation about z axis ¡ For rotation about x axis, x is unchanged ¡ For rotation about y axis, y is unchanged R = Rx(q) = Ry(q) =

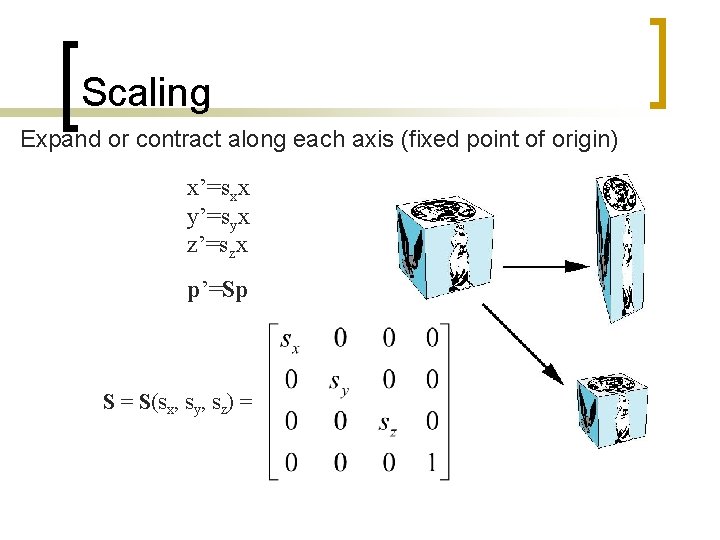
Scaling Expand or contract along each axis (fixed point of origin) x’=sxx y’=syx z’=szx p’=Sp S = S(sx, sy, sz) =

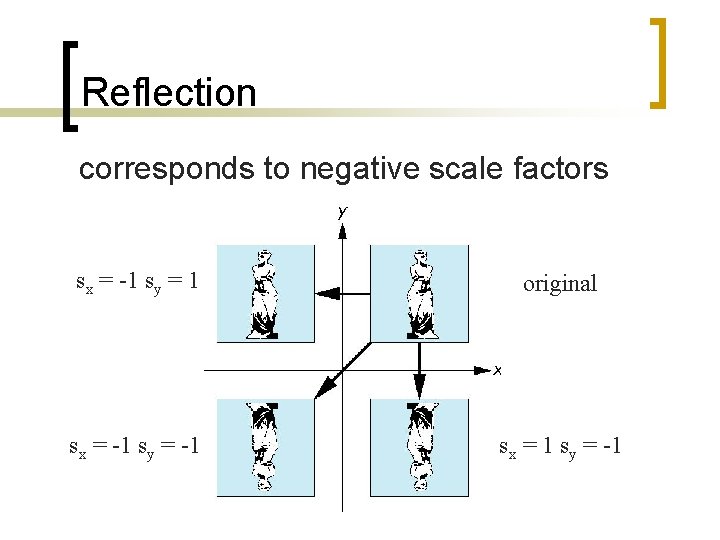
Reflection corresponds to negative scale factors sx = -1 sy = 1 original sx = -1 sy = -1 sx = 1 sy = -1

Inverses n Although we could compute inverse matrices by general formulas, we can use simple geometric observations -1 ¡ Translation: T (dx, dy, dz) = T(-dx, -dy, -dz) -1 ¡ Rotation: R (q) = R(-q) n Holds for any rotation matrix n Note that since cos(-q) = cos(q) and sin(-q)=-sin(q) R -1(q) = R T(q) ¡Scaling: S-1(sx, sy, sz) = S(1/sx, 1/sy, 1/sz)

Concatenation n. We can form arbitrary affine transformation matrices by multiplying together rotation, translation, and scaling matrices n. Because the same transformation is applied to many vertices, the cost of forming a matrix M=ABCD is not significant compared to the cost of computing Mp for many vertices p n. The difficult part is how to form a desired transformation from the specifications in the application

Order of Transformations n. Note that matrix on the right is the first applied n. Mathematically, the following are equivalent p’ = ABCp = A(B(Cp))

General Rotation About the Origin A rotation by q about an arbitrary axis can be decomposed into the concatenation of rotations about the x, y, and z axes R(q) = Rz(qz) Ry(qy) Rx(qx) y qx qy qz are called the Euler angles q v x z

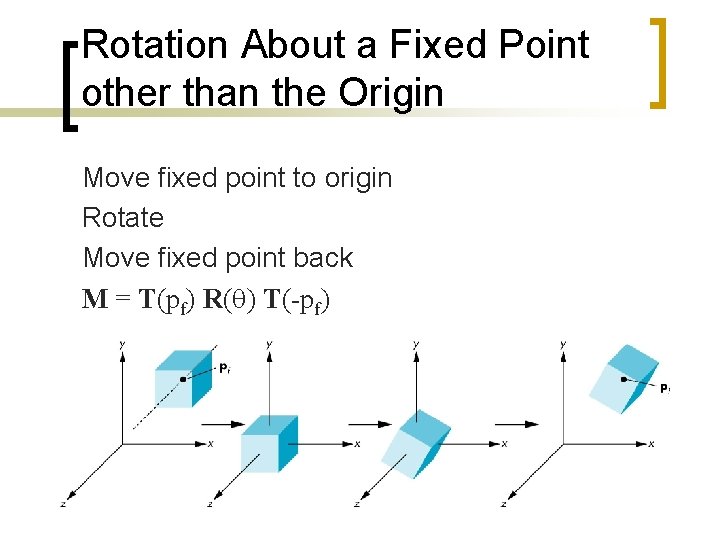
Rotation About a Fixed Point other than the Origin Move fixed point to origin Rotate Move fixed point back M = T(pf) R(q) T(-pf)

Instancing n. In modeling, we often start with a simple object centered at the origin, oriented with the axis, and at a standard size n. We apply an instance transformation to its vertices to Scale Orient Locate

Open. GL Matrices n. In Open. GL matrices are part of the state n. Three types ¡ Model-View (GL_MODEL_VIEW) ¡ Projection (GL_PROJECTION) ¡ Texture (GL_TEXTURE) (ignore for now) n. Single set of functions for manipulation n. Select which to manipulated by ¡ gl. Matrix. Mode(GL_MODEL_VIEW); ¡ gl. Matrix. Mode(GL_PROJECTION);

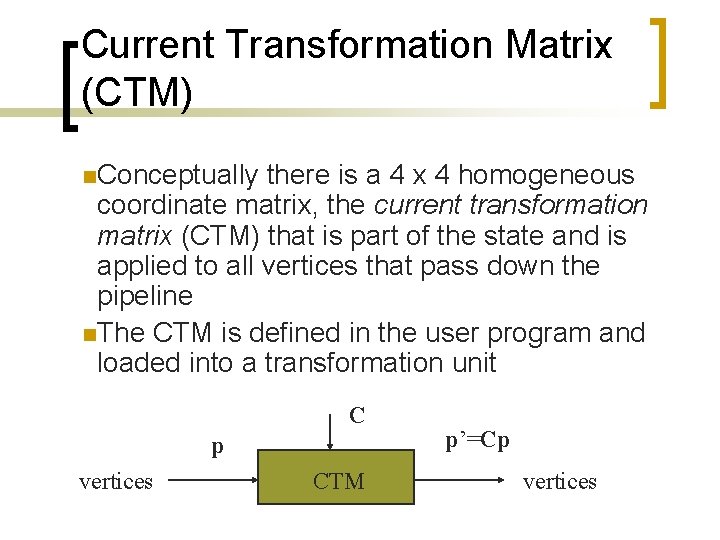
Current Transformation Matrix (CTM) n. Conceptually there is a 4 x 4 homogeneous coordinate matrix, the current transformation matrix (CTM) that is part of the state and is applied to all vertices that pass down the pipeline n. The CTM is defined in the user program and loaded into a transformation unit C p vertices CTM p’=Cp vertices

CTM operations n The CTM can be altered either by loading a new CTM or by postmutiplication Load an identity matrix: C I Load an arbitrary matrix: C M Load a translation matrix: C T Load a rotation matrix: C R Load a scaling matrix: C S Postmultiply by an arbitrary matrix: C CM Postmultiply by a translation matrix: C CT Postmultiply by a rotation matrix: C C R Postmultiply by a scaling matrix: C C S

Rotation about a Fixed Point Start with identity matrix: C I Move fixed point to origin: C CT -1 Rotate: C CR Move fixed point back: C CT Result: C = T -1 RT Each operation corresponds to one function call in the program. Note that the last operation specified is the first executed in the program

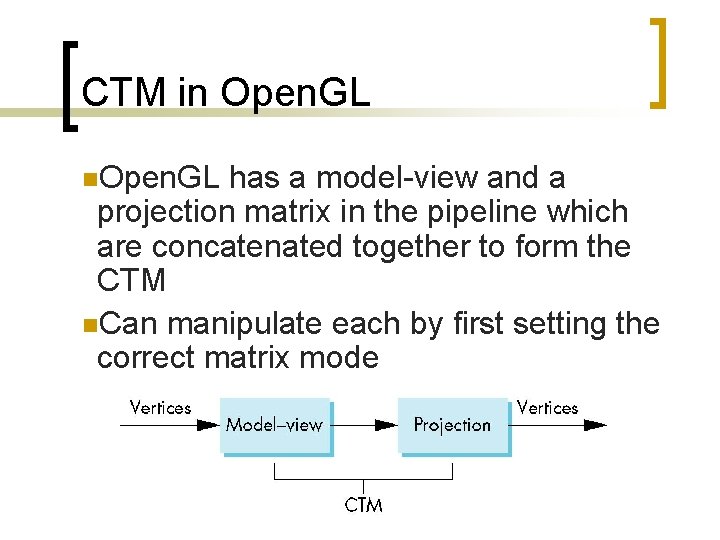
CTM in Open. GL n. Open. GL has a model-view and a projection matrix in the pipeline which are concatenated together to form the CTM n. Can manipulate each by first setting the correct matrix mode

Rotation, Translation, Scaling Load an identity matrix: gl. Load. Identity() Multiply on right: gl. Rotatef(theta, vx, vy, vz) theta in degrees, (vx, vy, vz) define axis of rotation gl. Translatef(dx, dy, dz) gl. Scalef( sx, sy, sz) Each has a float (f) and double (d) format (gl. Scaled)

Example n. Rotation about z axis by 30 degrees with a fixed point of (1. 0, 2. 0, 3. 0) gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); gl. Translatef(1. 0, 2. 0, 3. 0); gl. Rotatef(30. 0, 1. 0); gl. Translatef(-1. 0, -2. 0, -3. 0); n. Remember that last matrix specified in the program is the first applied

Arbitrary Matrices n. Can load and multiply by matrices defined in the application program gl. Load. Matrixf(m) gl. Mult. Matrixf(m) n. The matrix m is a one dimension array of 16 elements which are the components of the desired 4 x 4 matrix stored by columns n. In gl. Mult. Matrixf, m multiplies the existing matrix on the right

Matrix Stacks n. In many situations we want to save transformation matrices for use later ¡Traversing hierarchical data structures (Chapter 9) ¡Avoiding state changes when executing display lists n. Open. GL matrix ¡Access maintains stacks for each type of present type (as set by gl. Matrix. Mode) by gl. Push. Matrix() gl. Pop. Matrix()

Reading Back Matrices n. Can also access matrices (and other parts of the state) by enquiry (query) functions gl. Get. Integerv gl. Get. Floatv gl. Get. Booleanv gl. Get. Doublev gl. Is. Enabled n. For matrices, we use as double m[16]; gl. Get. Floatv(GL_MODELVIEW, m);

Using Transformations n. Example: use idle function to rotate a cube and mouse function to change direction of rotation n. Start with a program that draws a cube (colorcube. c) in a standard way ¡Centered at origin ¡Sides aligned with axes ¡Will discuss modeling in next lecture

main. c void main(int argc, char **argv) { glut. Init(&argc, argv); glut. Init. Display. Mode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH); glut. Init. Window. Size(500, 500); glut. Create. Window("colorcube"); glut. Reshape. Func(my. Reshape); glut. Display. Func(display); glut. Idle. Func(spin. Cube); glut. Mouse. Func(mouse); gl. Enable(GL_DEPTH_TEST); glut. Main. Loop(); }
![Idle and Mouse callbacks void spin Cube thetaaxis 2 0 if thetaaxis Idle and Mouse callbacks void spin. Cube() { theta[axis] += 2. 0; if( theta[axis]](https://slidetodoc.com/presentation_image_h2/52785e4be79baa5d65501c0bc7f79a58/image-33.jpg)
Idle and Mouse callbacks void spin. Cube() { theta[axis] += 2. 0; if( theta[axis] > 360. 0 ) theta[axis] -= 360. 0; glut. Post. Redisplay(); } void mouse(int btn, int state, int x, int y) { if(btn==GLUT_LEFT_BUTTON && state == GLUT_DOWN) axis = 0; if(btn==GLUT_MIDDLE_BUTTON && state == GLUT_DOWN) axis = 1; if(btn==GLUT_RIGHT_BUTTON && state == GLUT_DOWN) axis = 2; }
![Display callback void display gl ClearGLCOLORBUFFERBIT GLDEPTHBUFFERBIT gl Load Identity gl Rotateftheta0 Display callback void display() { gl. Clear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); gl. Load. Identity(); gl. Rotatef(theta[0],](https://slidetodoc.com/presentation_image_h2/52785e4be79baa5d65501c0bc7f79a58/image-34.jpg)
Display callback void display() { gl. Clear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); gl. Load. Identity(); gl. Rotatef(theta[0], 1. 0, 0. 0); gl. Rotatef(theta[1], 0. 0, 1. 0, 0. 0); gl. Rotatef(theta[2], 0. 0, 1. 0); colorcube(); glut. Swap. Buffers(); } Note that because of fixed form of callbacks, variables such as theta and axis must be defined as globals Camera information is in standard reshape callback

Using the Model-View Matrix n In Open. GL the model-view matrix is used to ¡ Position the camera n Can be done by rotations and translations but is often easier to use glu. Look. At (Chapter 5) ¡ Build models of objects n The projection matrix is used to define the view volume and to select a camera lens n Although both are manipulated by the same functions, we have to be careful because incremental changes are always made by postmultiplication

Smooth Rotation n From a practical standpoint, we often want to use transformations to move and reorient an object smoothly ¡ Problem: find a sequence of model-view matrices M 0, M 1, …. . , Mn so that when they are applied successively to one or more objects we see a smooth transition n For orientating an object, we can use the fact that every rotation corresponds to part of a great circle on a sphere ¡ Find the axis of rotation and angle ¡ Virtual trackball (see text)

Incremental Rotation n. Consider the two approaches ¡For a sequence of rotation matrices R 0, R 1, …. . , Rn , find the Euler angles for each and use Ri= Riz Riy Rix n. Not very efficient ¡Use the final positions to determine the axis and angle of rotation, then increment only the angle n. Quaternions can be more efficient than either

Next Class n n n Matrix stuff in Java 3 D Building models Assignment 1 is due Tuesday
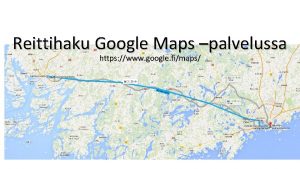
 Google maps reittihaku
Google maps reittihaku An operation that maps an original geometric figure
An operation that maps an original geometric figure Circles geometric measurement and geometric properties
Circles geometric measurement and geometric properties The basic geometric transformations are
The basic geometric transformations are Geometric transformations
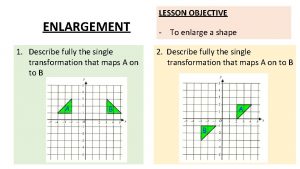
Geometric transformations Describe the fully single transformation
Describe the fully single transformation What is translation in computer graphics
What is translation in computer graphics Image geometry in digital image processing
Image geometry in digital image processing 2d geometric transformation in computer graphics ppt
2d geometric transformation in computer graphics ppt General pivot point rotation
General pivot point rotation Euclidean transformation in digital image processing
Euclidean transformation in digital image processing General lorentz transformation
General lorentz transformation Planos en cinematografia
Planos en cinematografia Where did general lee surrender to general grant?
Where did general lee surrender to general grant? Goole earth map
Goole earth map Types of weather maps
Types of weather maps Scale definition geography
Scale definition geography Story maps for reading comprehension
Story maps for reading comprehension Google maps ajax
Google maps ajax Understanding weather maps
Understanding weather maps Types of map in tourism
Types of map in tourism Thinking maps examples
Thinking maps examples What is the title of the map
What is the title of the map Strategy map template ppt free
Strategy map template ppt free As90953
As90953 Structure-measure: a new way to evaluate foreground maps
Structure-measure: a new way to evaluate foreground maps Google maps pythagorean theorem
Google maps pythagorean theorem Prince henry the navigator maps
Prince henry the navigator maps Openbiomaps
Openbiomaps Oranienburg map
Oranienburg map Lanl org chart
Lanl org chart Googlge drive
Googlge drive Oecd maps
Oecd maps Give one or two examples of how maps can be misused.
Give one or two examples of how maps can be misused. Ukhosted accelerated reader
Ukhosted accelerated reader Types of maps maths lit
Types of maps maths lit Maps and plans maths lit grade 12
Maps and plans maths lit grade 12 Scales maths lit
Scales maths lit Math thinking maps
Math thinking maps