GEOMETRIC TRANSFORMATIONS Yingcai Xiao Roadmap to Geometric Transformations






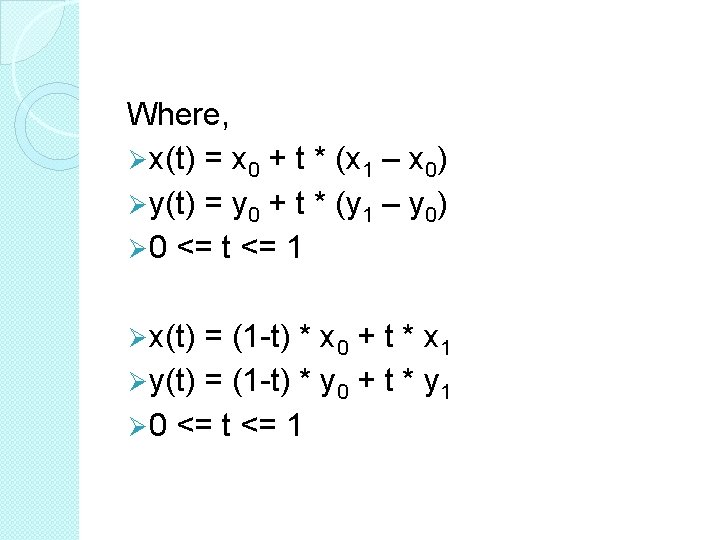








- Slides: 33

GEOMETRIC TRANSFORMATIONS Yingcai Xiao

Roadmap to Geometric Transformations �Start with 2 D GT �Extend to 3 D GT �Preview mathematics �Express GT in four type of notations ◦ ◦ Algebraic Matrix Logical Visual

Review of Mathematical Preliminaries Mathematical Notations Points: Vectors: directional lines P 1(x 1, y 1) P 0(x 0, y 0)

1. A vector has a direction and a length: Length: |V|=(x 2 + y 2)1/2 A unit vector: |V| = 1 e. g. : � Normalize a vector: 2. Add two vectors 3. Scalar Multiplication

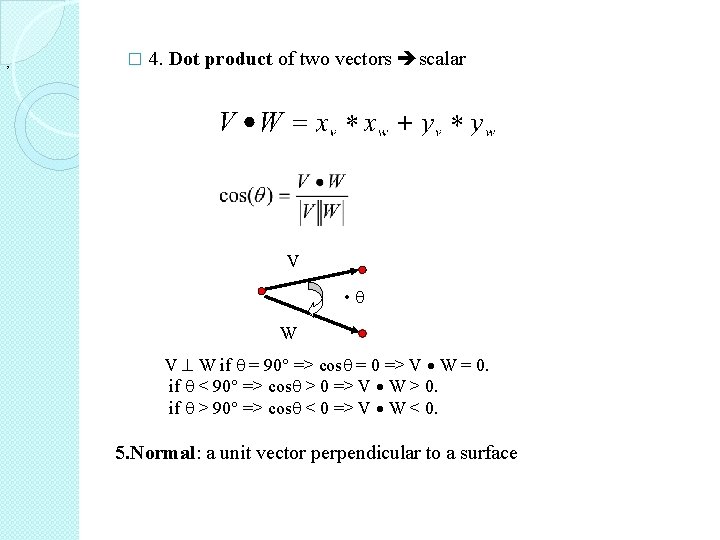
� , 4. Dot product of two vectors scalar V • W V W if = 90 => cos = 0 => V W = 0. if < 90 => cos > 0 => V W > 0. if > 90 => cos < 0 => V W < 0. 5. Normal: a unit vector perpendicular to a surface

. � Lines y = mx+b e. g. : y = x; ax+by+c=0 Let f(x, y) = ax + by + c A point p(xp, yp) is on the line if f(xp, yp) = 0. When b < 0: p(xp, yp) is above the line if f(xp, yp) < 0. p(xp, yp) is below the line if f(xp, yp) > 0. When b > 0: p(xp, yp) is above the line if f(xp, yp) > 0. p(xp, yp) is below the line if f(xp, yp) < 0.

Parametric Form: P(t)=P 0+t(P 1 -P 0); 0 <= t <= 1 P 1(x 1, y 1) P 0(x 0, y 0) P(t)=P 0+t(P 1 -P 0)
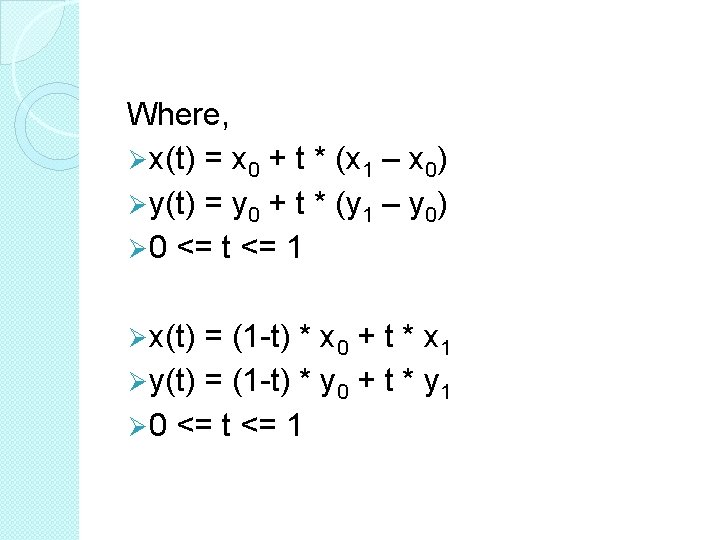

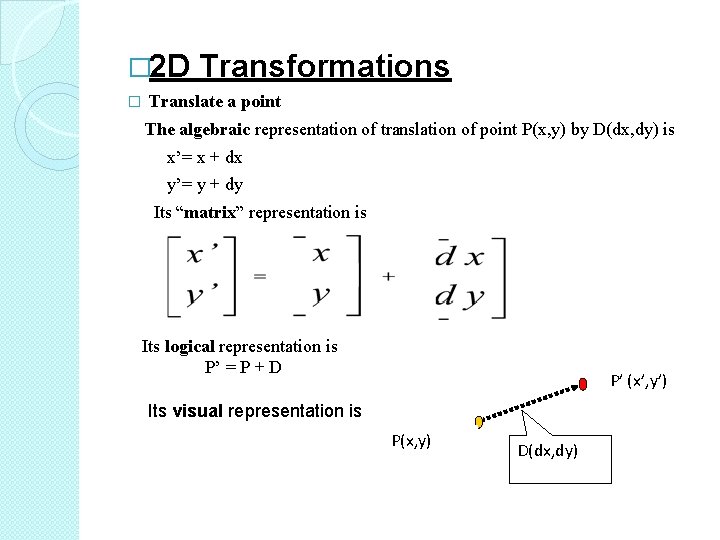
� 2 D Transformations � Translate a point The algebraic representation of translation of point P(x, y) by D(dx, dy) is x’= x + dx y’= y + dy Its “matrix” representation is Its logical representation is P’ = P + D Its visual representation is P’ (x’, y’) P(x, y) D(dx, dy)

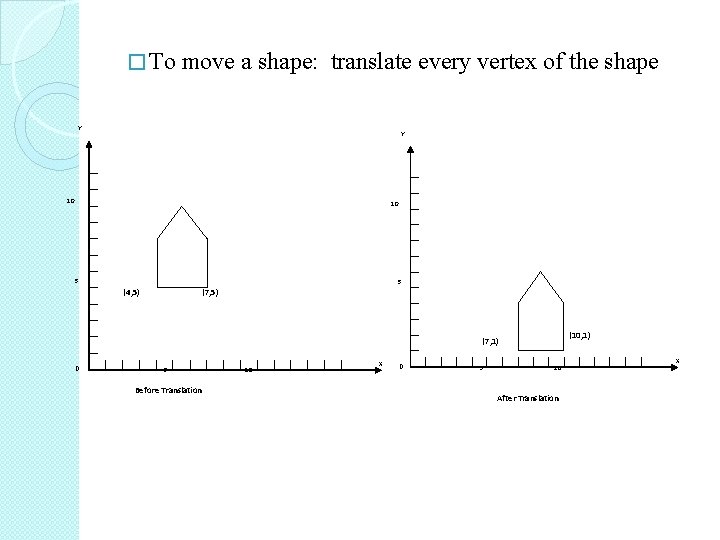
� To move a shape: translate every vertex of the shape Y Y 10 10 5 5 (4, 5) (7, 5) (10, 1) (7, 1) 0 5 Before Translation 10 X 0 5 10 After Translation X

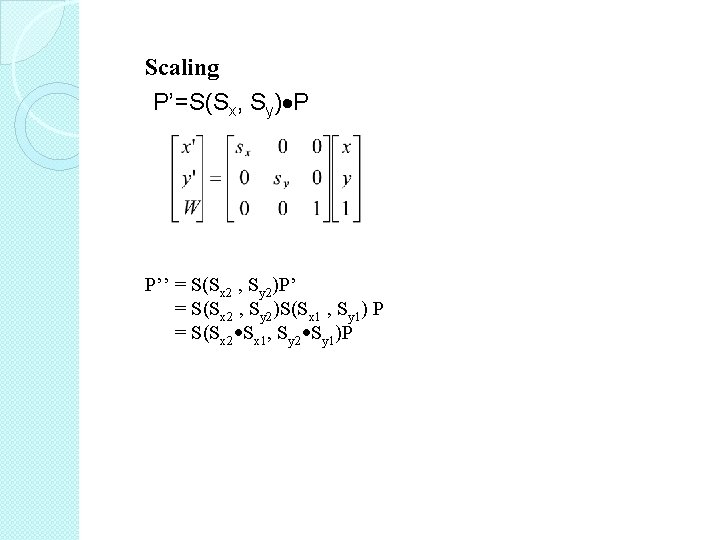
Scaling (relative to the origin) Scale a point P(x, y) by S(sx, sy) Algebraic: x’=sx* x � y’=sy* y Matrix: Logic: P’ = SP or P’ = S(sx, sy)P Scale a line P 0 P 1 (scale each point) P 0’=SP 0 P 1’=SP 1

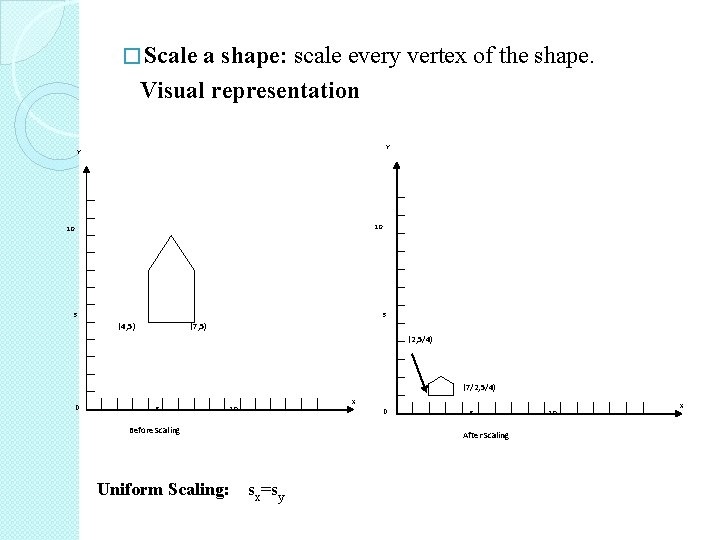
� Scale a shape: scale every vertex of the shape. Visual representation Y Y 10 10 5 5 (4, 5) (7, 5) (2, 5/4) (7/2, 5/4) 0 5 X 10 0 Before Scaling Uniform Scaling: 5 After Scaling sx=sy 10 X

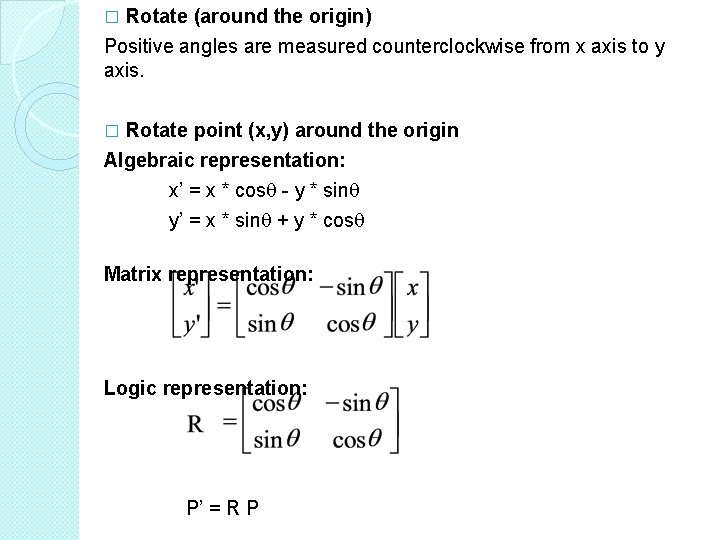
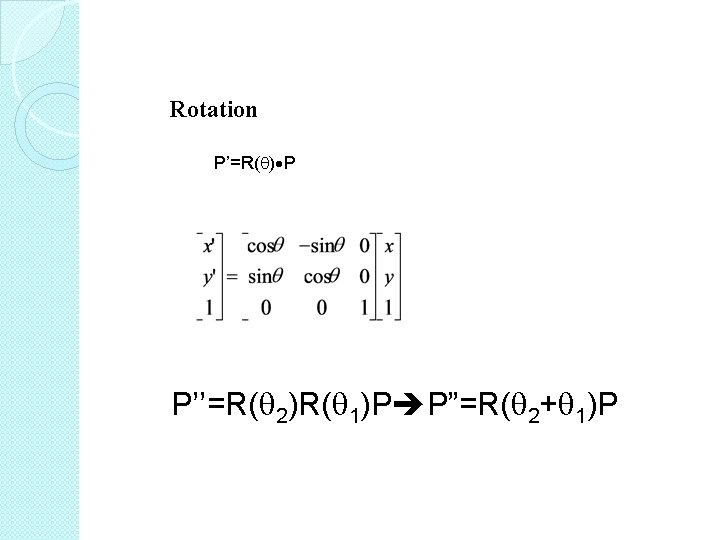
Rotate (around the origin) Positive angles are measured counterclockwise from x axis to y axis. � Rotate point (x, y) around the origin Algebraic representation: x’ = x * cos - y * sin y’ = x * sin + y * cos � Matrix representation: Logic representation: P’ = R P

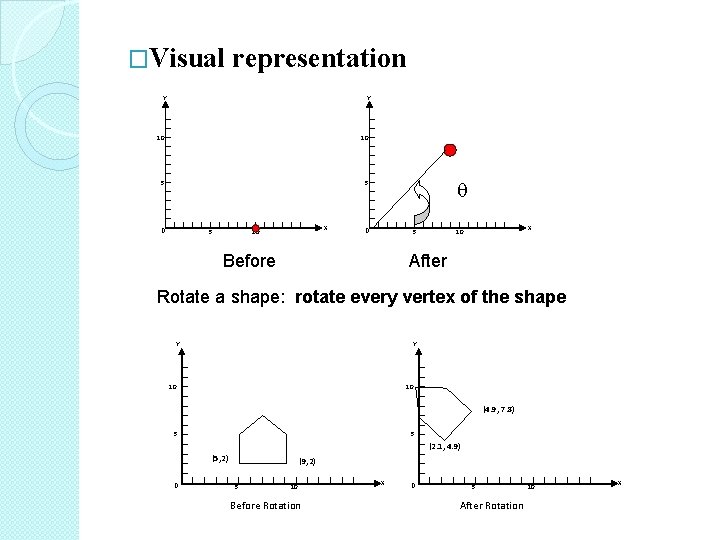
�Visual representation Y Y 10 10 5 5 0 5 X 10 0 5 Before X 10 After Rotate a shape: rotate every vertex of the shape Y Y 10 10 (4. 9, 7. 8) 5 5 (2. 1, 4. 9) (5, 2) 0 (9, 2) 5 10 Before Rotation X 0 5 After Rotation 10 X

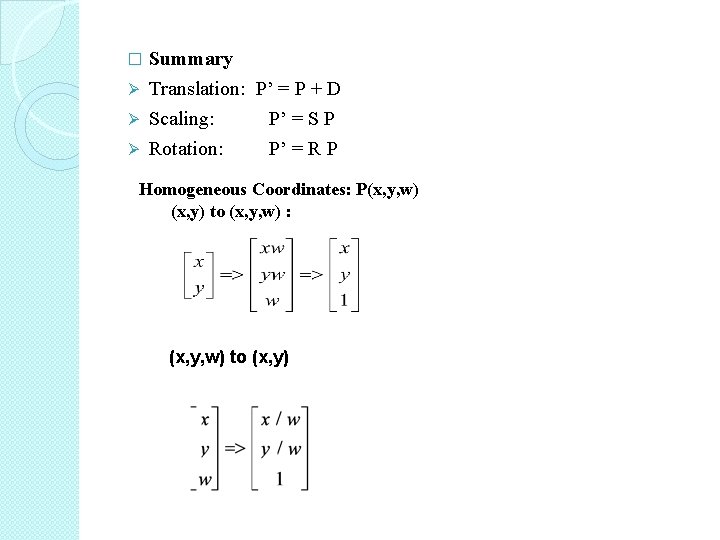
Summary Ø Translation: P’ = P + D Ø Scaling: P’ = S P Ø Rotation: P’ = R P � Homogeneous Coordinates: P(x, y, w) (x, y) to (x, y, w) : (x, y, w) to (x, y)

y’= y + dy w’=1 x’= x + dx P’’ = T(dx 2 , dy 2)P’ = T(dx 2 , dy 2) T(dx 1 , dy 1) P = T(dx 2+dx 1, dy 2+dy 1) P

Scaling P’=S(Sx, Sy) P P’’ = S(Sx 2 , Sy 2)P’ = S(Sx 2 , Sy 2)S(Sx 1 , Sy 1) P = S(Sx 2 Sx 1, Sy 2 Sy 1)P

Rotation P’=R( ) P P’’=R( 2)R( 1)P P”=R( 2+ 1)P

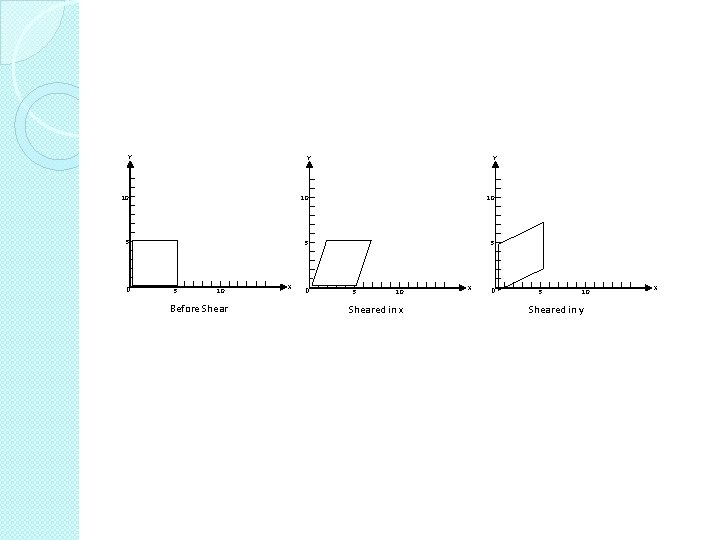
�Shear Transformation: SHx(a) and SHy(b) P’=SHx(a) P Shear in x against y by a (or an angle). x’ = x+ay y’ = y w’=1

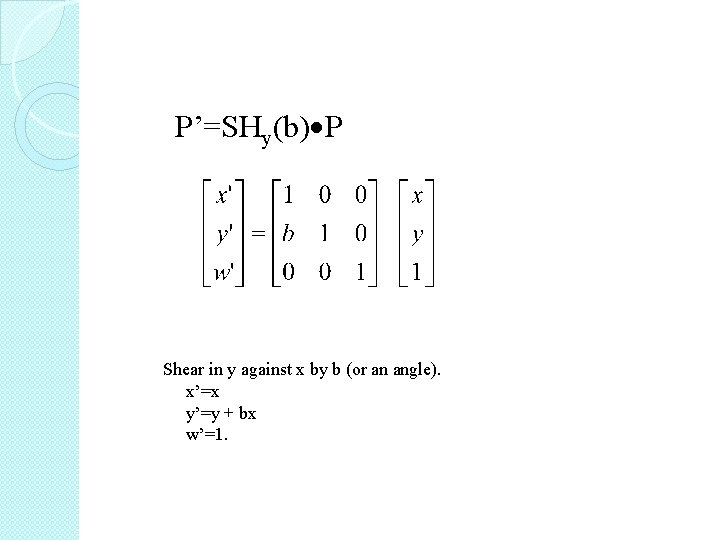
P’=SHy(b) P Shear in y against x by b (or an angle). x’=x y’=y + bx w’=1.

Y Y Y 10 10 10 5 5 5 0 5 10 Before Shear X 0 5 10 Sheared in x X 0 5 10 Sheared in y X

Rigid-body Transformation: T and R. � change: location, orientation; � not change: size, angle between elements. Affine Transformation: S, SH � change: size, location, angle; � not change: line (parallelism). � Note: uniform scaling is between the two. It changes size but not angle. � So far, our S, R, SH are all around the origin.

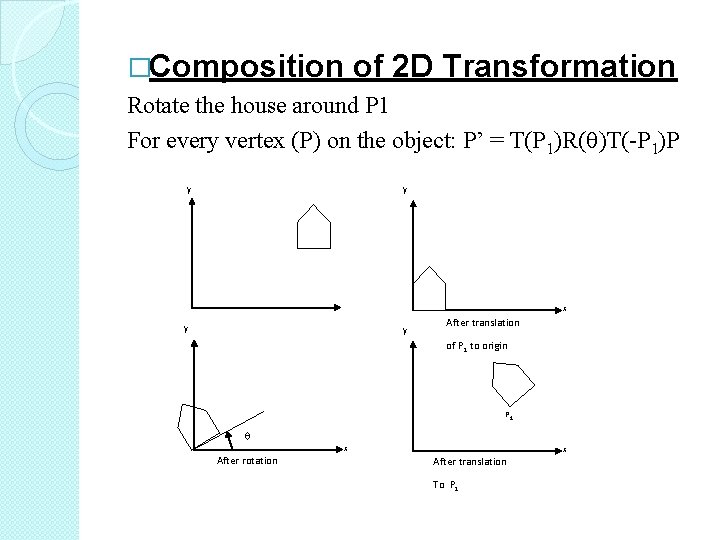
�Composition of 2 D Transformation Rotate the house around P 1 For every vertex (P) on the object: P’ = T(P 1)R( )T(-P 1)P y y x y y After translation of P 1 to origin P 1 After rotation x x After translation To P 1

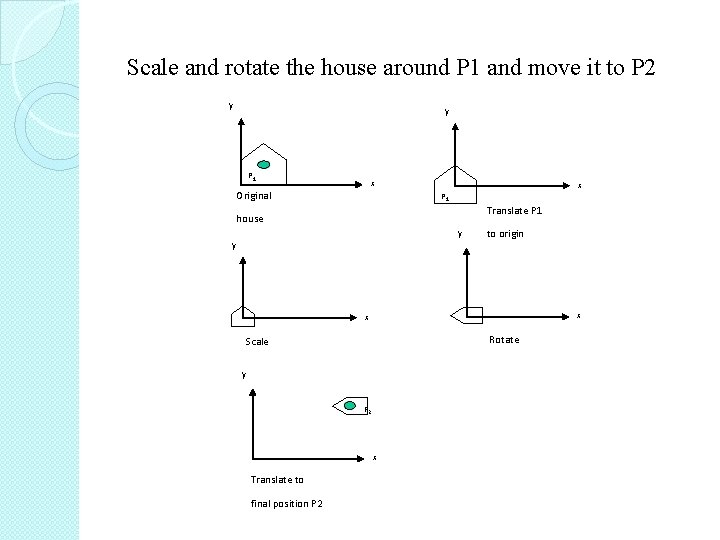
Scale and rotate the house around P 1 and move it to P 2 y y P 1 x Original x P 1 Translate P 1 house y to origin y x x Rotate Scale y P 2 x Translate to final position P 2

�For every vertex (P) on the object: P’ = T(P 2) R( )S(Sx, Sy)T(-P 1)P. �Swap the order of operations: not permitted, except uniform scaling (sx=sy) can be swapped with rotation.

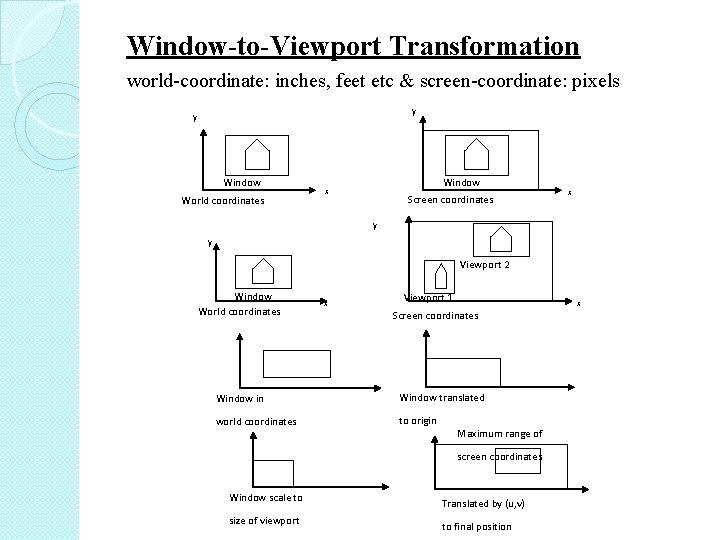
Window-to-Viewport Transformation world-coordinate: inches, feet etc & screen-coordinate: pixels y y Window World coordinates Window x Screen coordinates x y y Viewport 2 Window World coordinates x Viewport 1 x Screen coordinates Window in Window translated world coordinates to origin Maximum range of screen coordinates Window scale to size of viewport Translated by (u, v) to final position

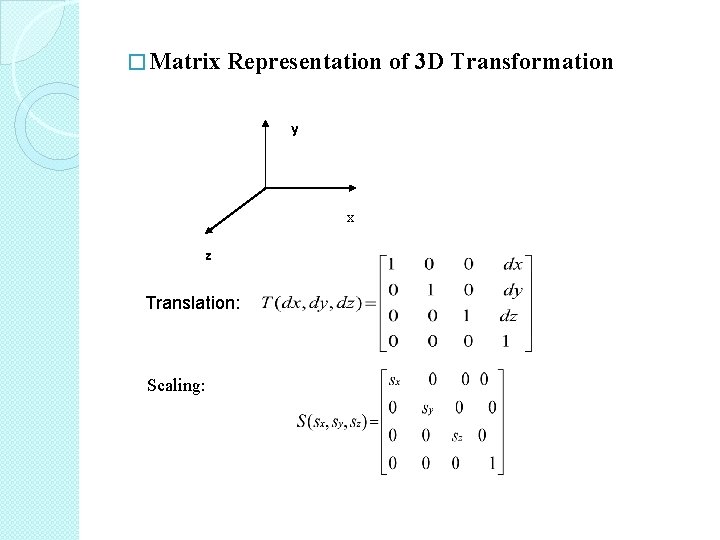
� Matrix Representation of 3 D Transformation y x z Translation: Scaling:

Rotation, around Z-axis: Rotation, around X-axis: Rotation, around Y-axis:

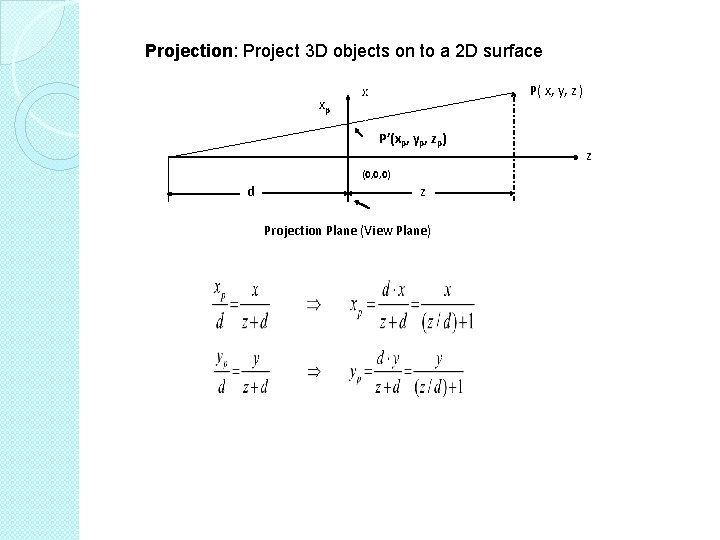
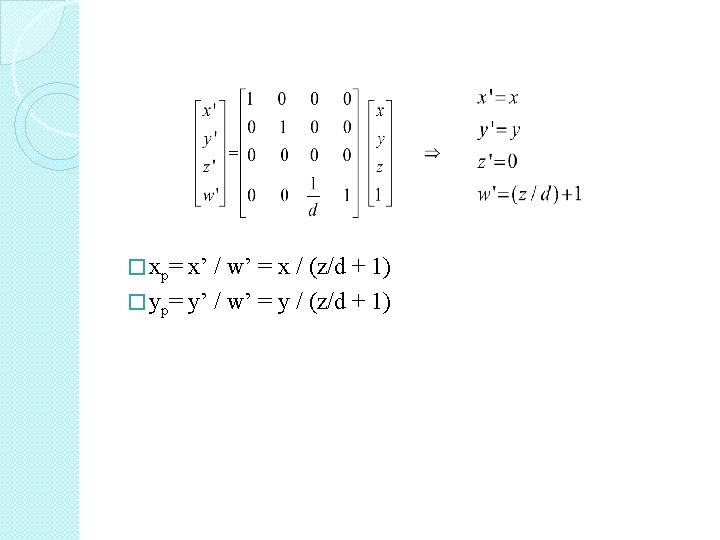
Projection: Project 3 D objects on to a 2 D surface xp P( x, y, z ) x P’(xp, yp, zp) (0, 0, 0) d z Projection Plane (View Plane) z


Foreshortening: The size of the projected object becomes smaller when the object moves away from the eye. P 1 P 2 P’ 1 z P’ 2 Perspective Projection: the projection that has the foreshortening effect.

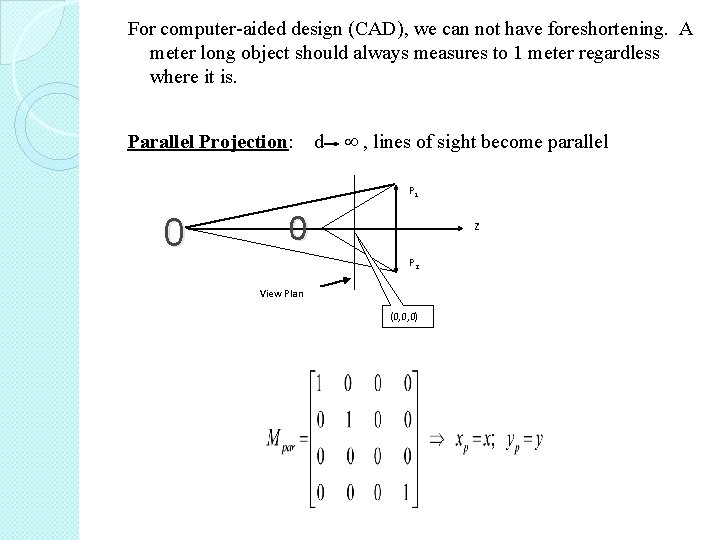
For computer-aided design (CAD), we can not have foreshortening. A meter long object should always measures to 1 meter regardless where it is. Parallel Projection: d , lines of sight become parallel P 1 0 0 z P 2 View Plan (0, 0, 0)

Summary � 2 D GT �Homogeneous coordinates � 3 D GT �Rigid body transformation �Affine transformation �Perspective Projection & Foreshortening �Parallel Projection
 Pixel array
Pixel array The basic geometric transformations are
The basic geometric transformations are Xiao height
Xiao height Maxims of annotation in corpus linguistics
Maxims of annotation in corpus linguistics Xiao qin auburn
Xiao qin auburn Scarlett xiao
Scarlett xiao Xiao hongchi poisoned blood therapy
Xiao hongchi poisoned blood therapy Xiao qin auburn
Xiao qin auburn Xiao outline
Xiao outline Xiao tao cos
Xiao tao cos Xiao tu
Xiao tu 510631
510631 Xiao game
Xiao game Angela xiao
Angela xiao Cunde xiao
Cunde xiao Xiao qin auburn
Xiao qin auburn Hong xiao semiconductor
Hong xiao semiconductor Xiao
Xiao Xiao ke gao md
Xiao ke gao md Bei xiao american university
Bei xiao american university Richard xiao
Richard xiao Sinan xiao
Sinan xiao Xiao team comp
Xiao team comp Xiao video game
Xiao video game Xiao qin auburn
Xiao qin auburn Geometry bootcamp answers
Geometry bootcamp answers Roadmap to success
Roadmap to success Azure sql server advanced data security
Azure sql server advanced data security Dmaic roadmap
Dmaic roadmap Career roadmap osu
Career roadmap osu Roadmap for change
Roadmap for change Produktroadmap
Produktroadmap Pmi kentucky
Pmi kentucky Vlsi roadmap
Vlsi roadmap























































