5 Phonons Thermal Properties Phonon Heat Capacity Anharmonic






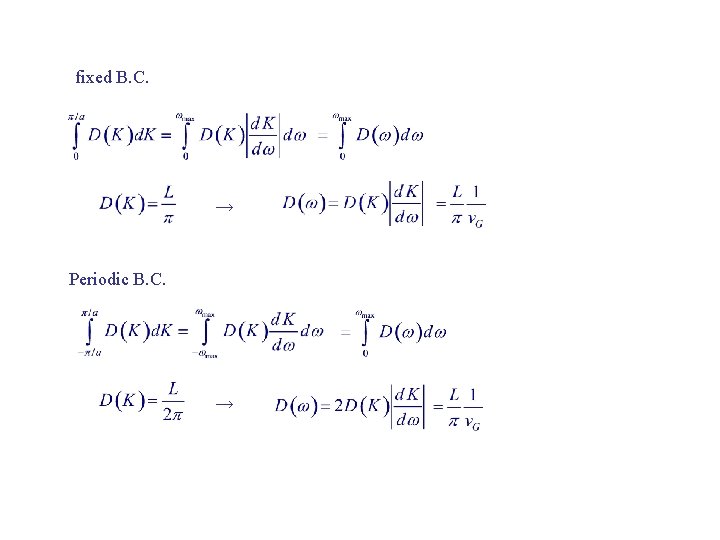








- Slides: 29

5. Phonons Thermal Properties • Phonon Heat Capacity • Anharmonic Crystal Interactions • Thermal Conductivity

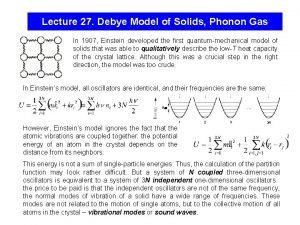
Phonon Heat Capacity • • Planck Distribution Normal Mode Enumeration Density of States in One Dimension Density of States in Three Dimensions Debye Model for Density of States Debye T 3 Law Einstein Model of the Density of States General Result for D(ω)

where = Thermal expansivity = isothermal compressibility = 1/ B B = Bulk modulus α = linear (1 -D) thermal expansivity

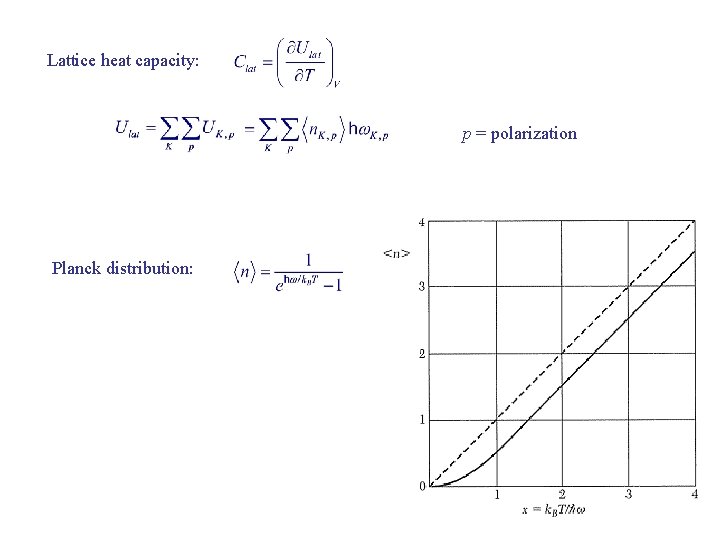
Lattice heat capacity: p = polarization Planck distribution:

Planck Distribution System at constant T Canonical ensemble : Boltzmann factor For a set of identical harmonic oscillators Nn = number of oscillators in the nth excited state when system is in thermal equilibrium Probability of an oscillator in the nth excited state: Occupation number:

Normal Mode Enumeration

Density of States in One Dimension Fixed boundary problem of N+1 particles. N = 10 → with Number of allowed K for non-stationary solutions is N– 1 = Number of mobile atoms Polarization p : 1 long, 2 trans

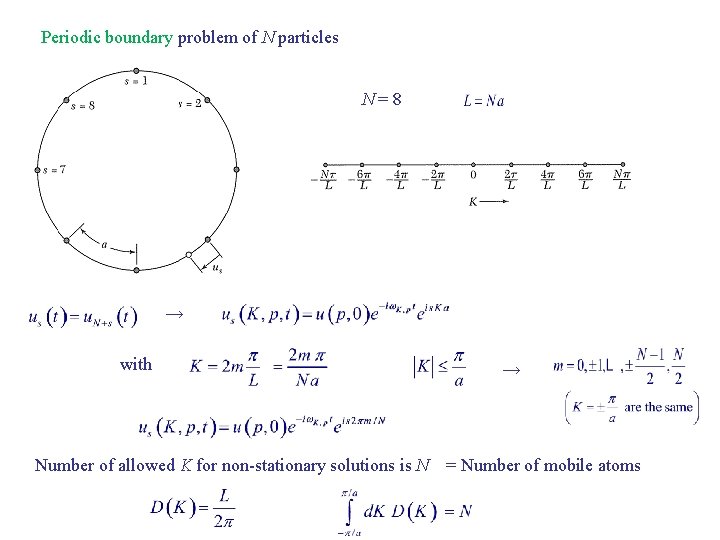
Periodic boundary problem of N particles N=8 → with → Number of allowed K for non-stationary solutions is N = Number of mobile atoms
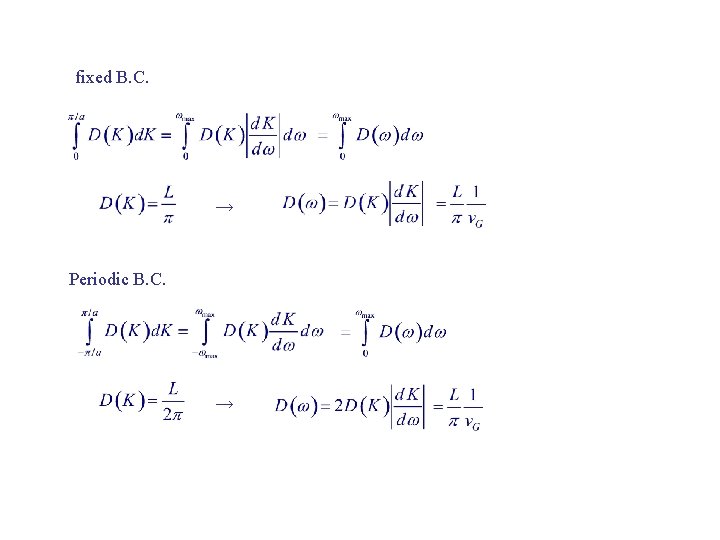
fixed B. C. → Periodic B. C. →

Density of States in Three Dimensions Periodic B. C. ; N 3 cells in cube of side L → density of states in K-space is Number of modes per polarization lying between ω and ω + d ω is → density of states in ω-space is For isotropic materials, →

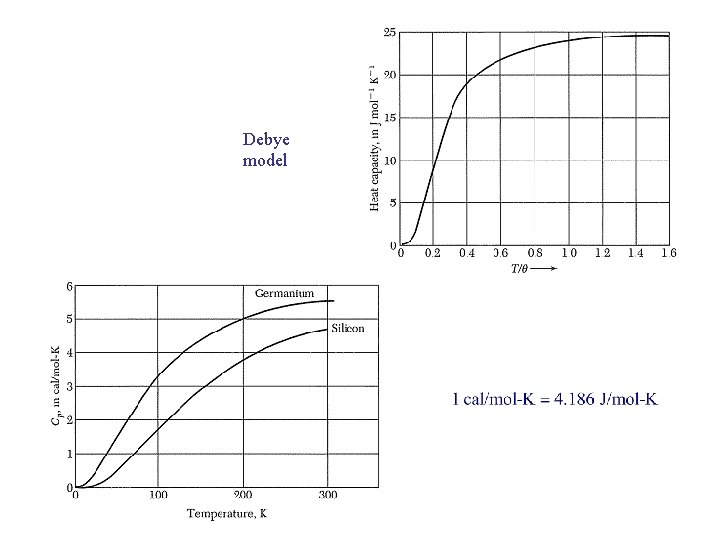
Debye Model for Density of States Debye model: v velocity of sound (for a given type of polarization) For a crystal of N primitive cells: → Debye frequency

Thermal (vibrational) energy Debye integrals: See Ex on Zeta functions, Arfken where θ Debye temperature for each acoustic branch

Debye model

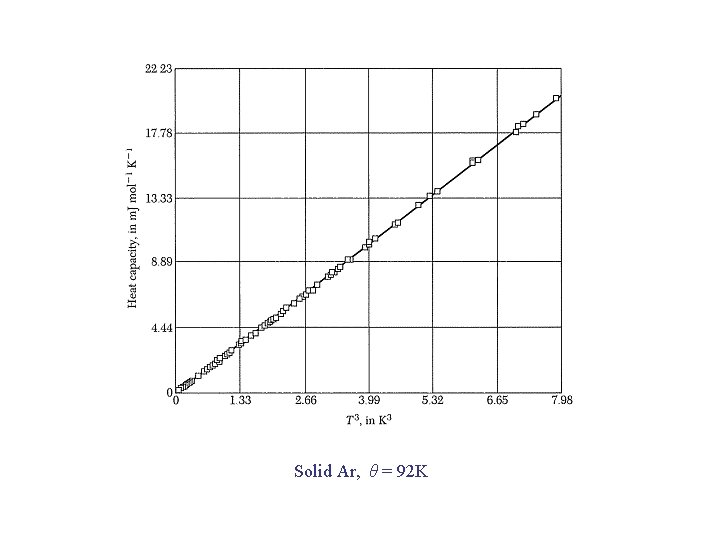
Debye T 3 Law For low T, x. D → : → for each acoustic branch To account for all 3 acoustic branches, we set and so that Good for T < θ /50

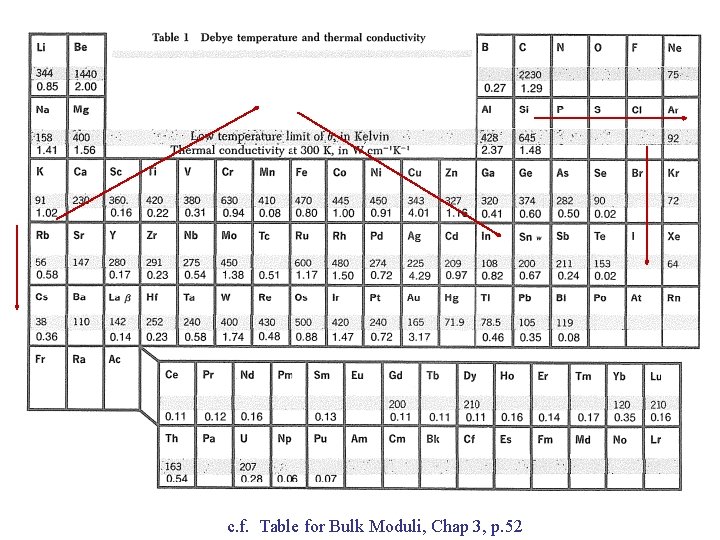
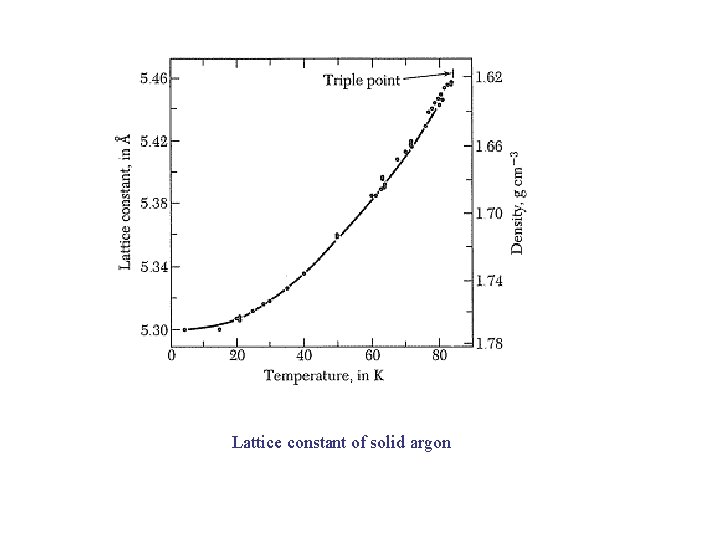
Solid Ar, θ = 92 K

c. f. Table for Bulk Moduli, Chap 3, p. 52

Qualitative Explanation of the T 3 Law Of the 3 N modes, only a fraction (KT /KD ) 3 = ( T / θ )3 is excited. →

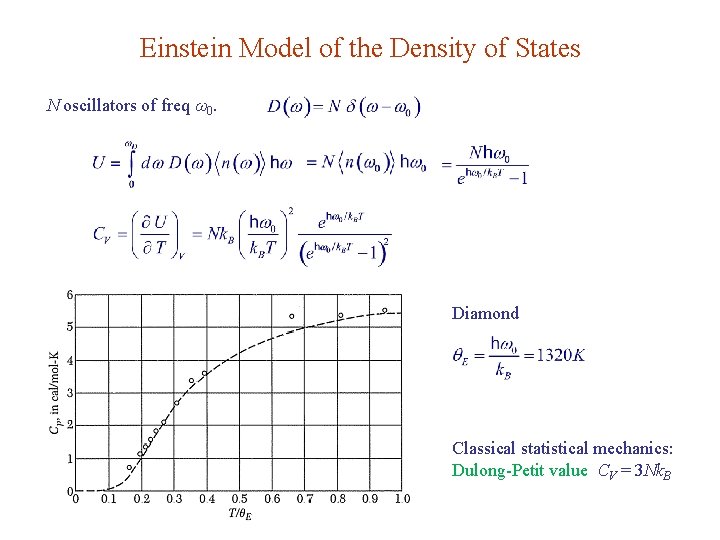
Einstein Model of the Density of States N oscillators of freq ω0. Diamond Classical statistical mechanics: Dulong-Petit value CV = 3 Nk. B

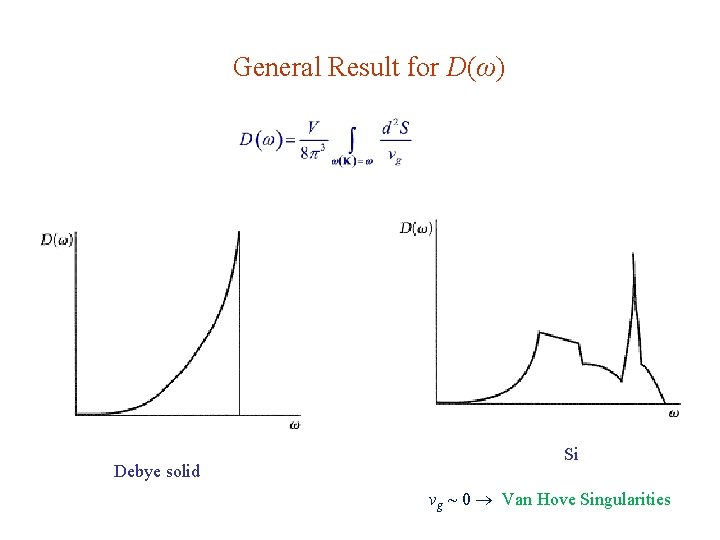
General Result for D(ω) Debye solid Si vg ~ 0 Van Hove Singularities

Anharmonic Crystal Interactions Harmonic (Linear) Waves: • Normal modes do not decay. • Normal modes do not interact. • No thermal expansion. • Adiabatic & isothermal elastic constants are equal. • Elastic constants are independent of P and T. • C → constant for T > θ. Deviation from harmonic behavior → Anharmonic effects

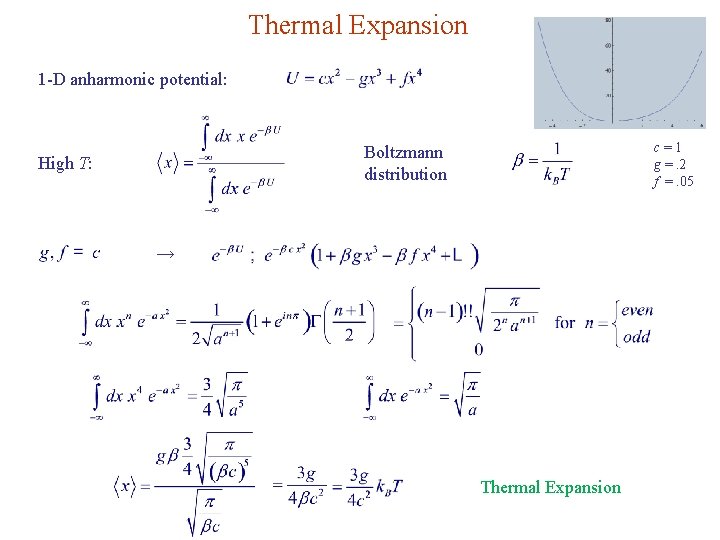
Thermal Expansion 1 -D anharmonic potential: c=1 g =. 2 f =. 05 Boltzmann distribution High T: → Thermal Expansion

Lattice constant of solid argon

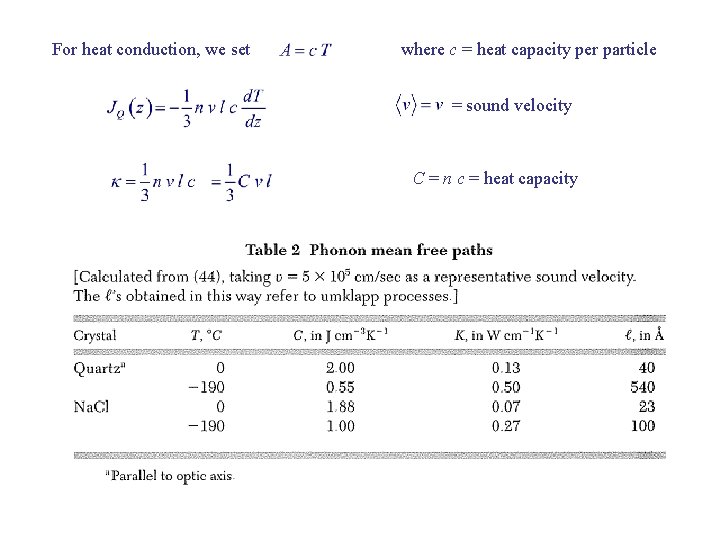
Thermal Conductivity Heat current density: κ = Thermal conductivity coefficient For phonons, JQ = JU. Key features of kinetic theory (see L. E. Reichl, “A Modern Course of Statistical Mechanics”, § 13. 4 ): 1. Quantities not conserved in particle collisions are quickly thermalized to (global) equilibrium values. (e. g. , velocity directions & magnitudes ) 2. Conserved quantities can remain out of global equilibrium (e. g. , stay in local equilibrium. They get transported spatially in the presence of a “gradient”. 3. MFP is determined by collisions that do not conserve the total momenta of particles. Net amount of A(z) transported across the x-y plane at z 0 in the +z direction per unit area per unit time: Δz = distance above/below plane at which particle suffered last collision. n = particle density, l = mean free path, a = some constant. b. A = 1/3 is determined from self diffusion

For heat conduction, we set where c = heat capacity per particle = sound velocity C = n c = heat capacity

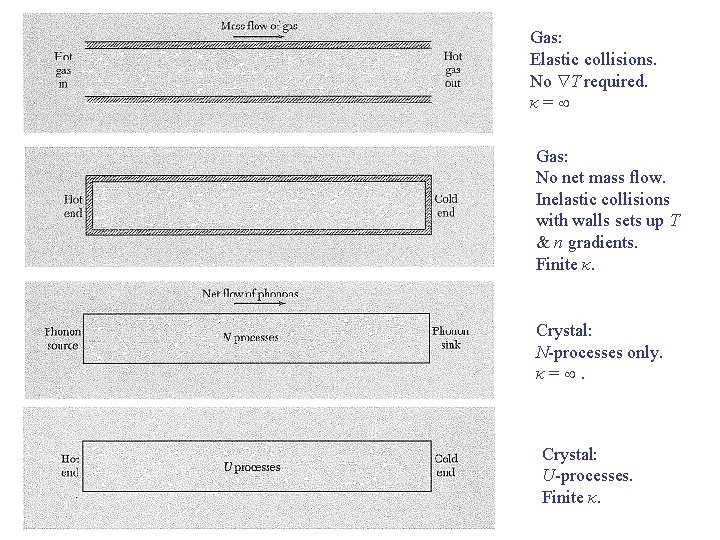
Thermal Resistivity of Phonon Gas Harmonic phonons: mfp l determined by collisions with boundaries & imperfections. Anharmonic phonons: only U-processes contribute.

Gas: Elastic collisions. No T required. κ= Gas: No net mass flow. Inelastic collisions with walls sets up T & n gradients. Finite κ. Crystal: N-processes only. κ=. Crystal: U-processes. Finite κ.

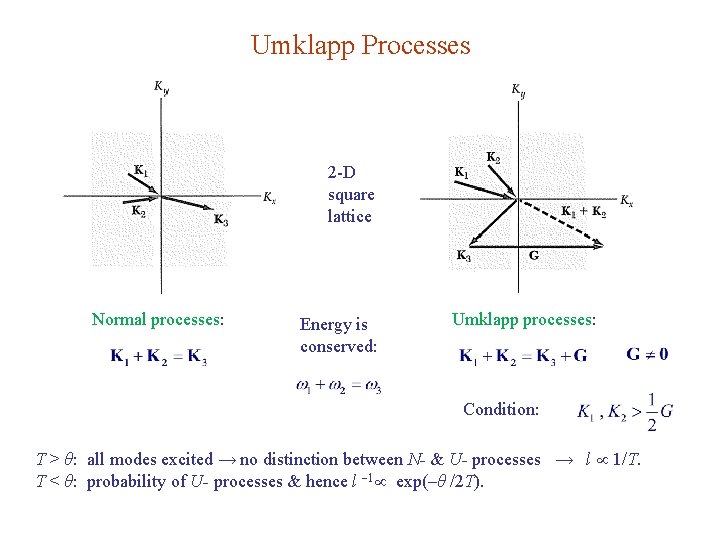
Umklapp Processes 2 -D square lattice Normal processes: Energy is conserved: Umklapp processes: Condition: T > θ: all modes excited → no distinction between N- & U- processes → l 1/T. T < θ: probability of U- processes & hence l 1 exp(–θ /2 T).

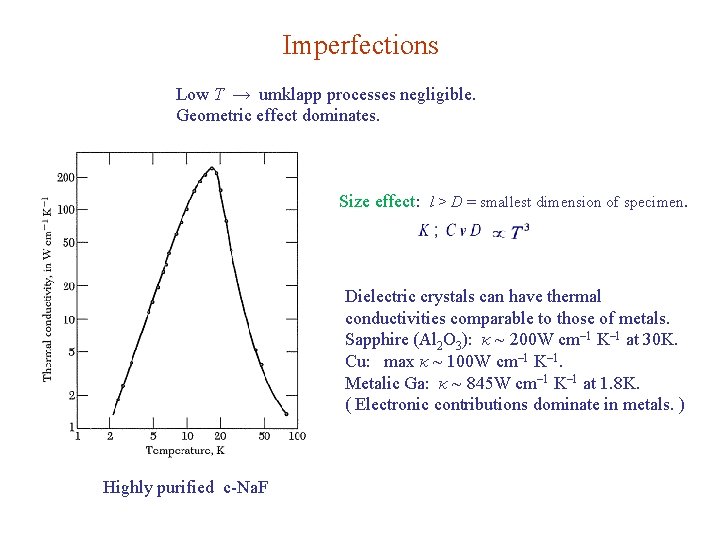
Imperfections Low T → umklapp processes negligible. Geometric effect dominates. Size effect: l > D = smallest dimension of specimen. Dielectric crystals can have thermal conductivities comparable to those of metals. Sapphire (Al 2 O 3): κ ~ 200 W cm– 1 K– 1 at 30 K. Cu: max κ ~ 100 W cm– 1 K– 1. Metalic Ga: κ ~ 845 W cm– 1 K– 1 at 1. 8 K. ( Electronic contributions dominate in metals. ) Highly purified c-Na. F

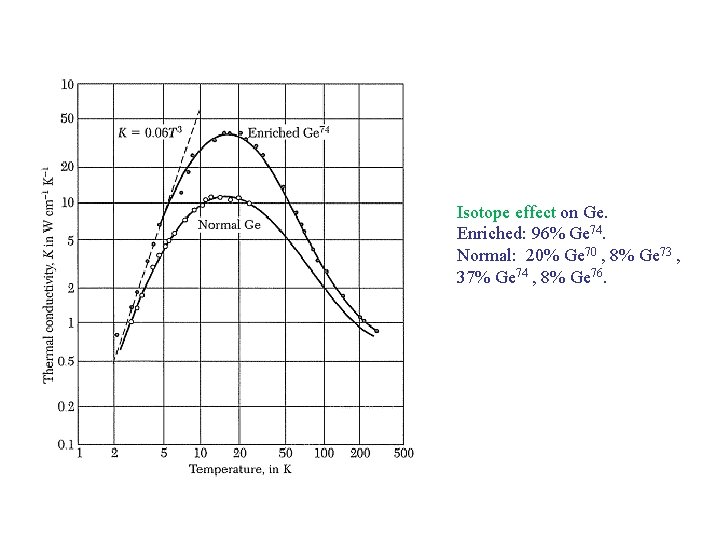
Isotope effect on Ge. Enriched: 96% Ge 74. Normal: 20% Ge 70 , 8% Ge 73 , 37% Ge 74 , 8% Ge 76.
 Phonon heat capacity
Phonon heat capacity Main difference between hofmann and curtius rearrangement
Main difference between hofmann and curtius rearrangement Optical vs acoustic phonons
Optical vs acoustic phonons Phonons of physical fitness
Phonons of physical fitness Properties of heat
Properties of heat Phonon hall effect
Phonon hall effect Debye model of solids
Debye model of solids Vibrations of crystals with monatomic basis
Vibrations of crystals with monatomic basis Phonon momentum
Phonon momentum Quasi electron
Quasi electron Phonon momentum
Phonon momentum Section 3 using thermal energy answers
Section 3 using thermal energy answers Thermal transfer vs direct thermal printing
Thermal transfer vs direct thermal printing What is the unit of thermal capacity
What is the unit of thermal capacity What is the unit of thermal capacity
What is the unit of thermal capacity The unit of specific heat capacities
The unit of specific heat capacities Latent heat of lead
Latent heat of lead Design capacity and effective capacity examples
Design capacity and effective capacity examples Difference between heat and thermal energy
Difference between heat and thermal energy Specific heat capacity of lead j/kg c
Specific heat capacity of lead j/kg c Difference between heat and thermal energy
Difference between heat and thermal energy What is heat energy?
What is heat energy? What is the difference between thermal energy and heat?
What is the difference between thermal energy and heat? How to solve for thermal energy
How to solve for thermal energy What is heat
What is heat Heat thermal energy and temperature
Heat thermal energy and temperature Thermal energy vs heat
Thermal energy vs heat Heat thermal energy and temperature
Heat thermal energy and temperature Formula formula
Formula formula Thermal energy vs heat energy
Thermal energy vs heat energy