15 251 Some Great Theoretical Ideas in Computer



![Public Key Cryptography Secret M Private Key Public Key P EP[M] Public Key Cryptography Secret M Private Key Public Key P EP[M]](https://slidetodoc.com/presentation_image_h/9c215df7485906a6cf57eb09a8039323/image-4.jpg)





![Modular Equivalence a b [mod n] (a mod n) = (b mod n) n|(a-b) Modular Equivalence a b [mod n] (a mod n) = (b mod n) n|(a-b)](https://slidetodoc.com/presentation_image_h/9c215df7485906a6cf57eb09a8039323/image-11.jpg)

































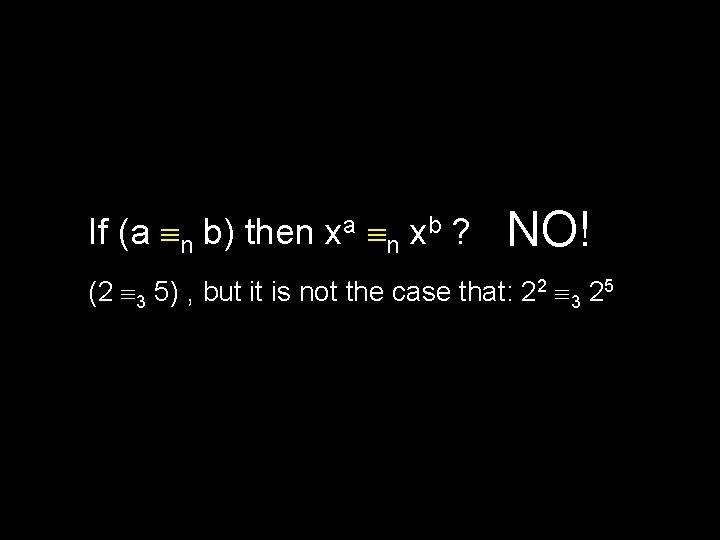




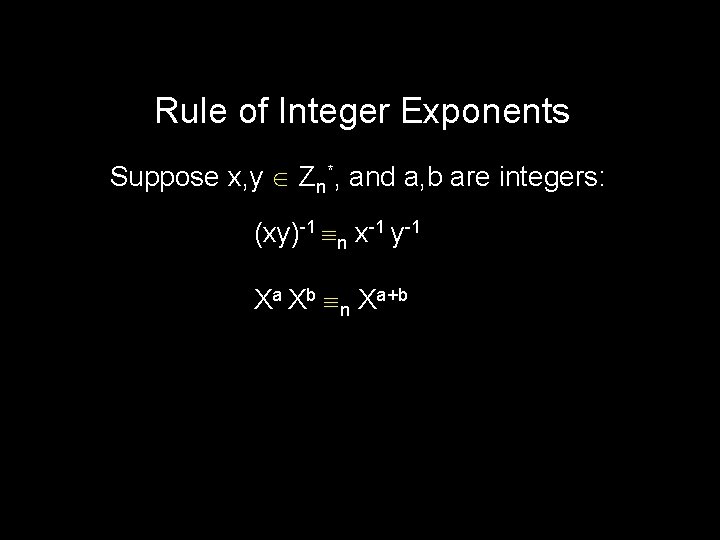


- Slides: 59

15 -251 Some Great Theoretical Ideas in Computer Science for

Modular Arithmetic and the RSA Cryptosystem Lecture 17 (March 18, 2008) p-1 p 1

Public Key Cryptography -----BEGIN PGP PRIVATE KEY BLOCK----Version: PGP 8. 1 - not licensed for commercial use: www. pgp. com l. QHNBEOed. R 4 RBAC 6 bfed 3 ULz. Ow. VF/Bouy. O 8 kfs 8 wk. Omk 3 va. MF 6+6 Jye. EJqy. Ima. Vh p. Vh. U 7 lst 6 Qt. XTy. AF 734 Ft. Cl. M/9 Dq 9 Dn 7 GDo. O 3 E 9+n. GVO 7 w. J 1 OT+X 4 lgkoi. M 68 WWG -----BEGIN PGP PUBLIC KEY BLOCK----eio. T 958 Hg 0 zq 0 Kqu. HUBFM+Kldc+nr 0 e 0 Q 6 u. Cgw. IYM 7 o. H 60/WX 8 e 2 Wnvycw. Cgzba 0 Version: PGP 8. 1 - not licensed for commercial use: www. pgp. com k. Rzx. Ntmw 9 w 9 IEQUk 9 pa 2 CK 8 D/2 Fj. Rxt. EDN 6 n. Y 7/l 1 w. Urk. Mj. I/u. XYns. NWwr. IAbw. Hp qh. UZQYst 27 Xpw. Npl. Am. I 6 Yu. S+3 O+L 4 vg. URj 1 h. Vcn. NG+2 b. ZXjbt 4 Fg 3 RLhr. TV/jiu. L m. QGi. BEOed. R 4 RBAC 6 bfed 3 ULz. Ow. VF/Bouy. O 8 kfs 8 wk. Omk 3 va. MF 6+6 Jye. EJqy. Ima. Vh oh. Bay. AAd. ZZ 4+72 Cja 1+18 xp 700 GVTF 96 j. Yc 8 d. Iox. Nx 1 Ag. Hz. QUffj 3 Gnsc. Azo 7 ud 3 p. Vh. U 7 lst 6 Qt. XTy. AF 734 Ft. Cl. M/9 Dq 9 Dn 7 GDo. O 3 E 9+n. GVO 7 w. J 1 OT+X 4 lgkoi. M 68 WWG Hy. YHA/9 s. I 6 Gijh/ubr 1 q. Tz. Hw. ZPdil. Djfn. Ey. Qw. R 6+for. UUegw. CO 0 Yaws. C 2 l. G 6 F 7 MG eio. T 958 Hg 0 zq 0 Kqu. HUBFM+Kldc+nr 0 e 0 Q 6 u. Cgw. IYM 7 o. H 60/WX 8 e 2 Wnvycw. Cgzba 0 q 3 RHn. JSw. I 3 Di. H/g. Y 5 b. Yk 3 Xxhink. Kxqk 54 Di. L 6 vr. HIw/E 9 J 6 Raz. Y+ocic. LRZ+6 Xj. O k. Rzx. Ntmw 9 w 9 IEQUk 9 pa 2 CK 8 D/2 Fj. Rxt. EDN 6 n. Y 7/l 1 w. Urk. Mj. I/u. XYns. NWwr. IAbw. Hp JPXp. K 8 s 2 v 64 p. H 5 gyrsf. ANw. STTy. ECPx/hp 2 G+0 BW/mt. MU+Jq. FPP 8 DAw. Kvg. RN 08 a. TW qh. UZQYst 27 Xpw. Npl. Am. I 6 Yu. S+3 O+L 4 vg. URj 1 h. Vcn. NG+2 b. ZXjbt 4 Fg 3 RLhr. TV/jiu. L 1 WAW 5/ak/URD 4 OAOT 6 OXlyg 4 Ywha. Jodb 9 vfwck 4 V 8 bn. NLVNhb. XBs. ZSBTZWN 1 cm. VC oh. Bay. AAd. ZZ 4+72 Cja 1+18 xp 700 GVTF 96 j. Yc 8 d. Iox. Nx 1 Ag. Hz. QUffj 3 Gnsc. Azo 7 ud 3 b. GFja 2 Jve. CBQR 1 Aga 2 V 5 PGlu. Zm 9 AZWxkb 3 Mu. Y 29 t. Pp 0 DJg. RDnn. Wk. EAg. Ax. Iw. Ism. EC Hy. YHA/9 s. I 6 Gijh/ubr 1 q. Tz. Hw. ZPdil. Djfn. Ey. Qw. R 6+for. UUegw. CO 0 Yaws. C 2 l. G 6 F 7 MG m. LGf. QMH 6 Gf. Nqn 8 XG 9/bv. T/n. L/m 7 Tj. UVv 1 JGr. KDASb. ASs. Pl. YLn. Del 4 opyp 24 Azu 5 x q 3 RHn. JSw. I 3 Di. H/g. Y 5 b. Yk 3 Xxhink. Kxqk 54 Di. L 6 vr. HIw/E 9 J 6 Raz. Y+ocic. LRZ+6 Xj. O n. Q 0/Qls. Oifm. Xj. INc. Wz. Nt. Wc. Jk. W 3 r. Bam. P 1 Vw 6 Zhx. N 8 e 1 ARRrxw. On 42 V/yn/Ho. MFH 0 O JPXp. K 8 s 2 v 64 p. H 5 gyrsf. ANw. STTy. ECPx/hp 2 G+0 BW/mt. MU+Jq. FPM 0 t. U 2 Ftc. Gxl. IFNl Hhm 2 M 5 r 8 W/r. Oxo 4 d. Pd. KPm. RPd. Ma. PVMndg. M 8 Wc. OGPJ 6 Tb. Mb 4 g 9 hphb+E 4 o 3 gl. I 6 fh. P Y 3 Vy. ZUJs. YWNr. Ym 94 IFBHUCBr. ZXk 8 a. W 5 mb 0 Blb. GRvcy 5 jb 20+wkk. EEBECABMCm. QEF 41 GZy 57 w. Wd. KY 9 Dn. Q 3 W 2 PGo. Fa. FAl. Qdy. Atekz. Omixp 2/j. Xpq 4+br 9 Yd 088 Unp 2 sw 4 Z Ak. Oeda. QJEKl 84 Zsq. Net 0 AAAROg. Cgg. Fc. JOrmv. Nvpdm. ADv 0 i. Ez. VUVci+g. Ao. JDD 9 wbm 56 j 8 s. Ab. Tk 7 NFpc. TUSxsn. FXpi. Gr 0 Wk. V+qf. Dy. YTBv. En. FXItei. Th. AWYz. Jgge 6 Tb 6 qz. L WOq 7 M 06 k 4 r. SOZSj 2 me 0 Gu. QINBEOeda. QQCADEj. Aiy. YQKYs. Z 9 Awfo. Z 82 qfxcb 39 u 9 P 1 Xj. D 5 u. R 1 z 2 Fg. Tw. ACAgf/f. GBk. Ve 8 y. ETYw. ARrcn 0 x. Xv 991 AEv. A 4 wl. NI 0/gyg. JKXx. TV +cv+bt. ONRW/Ukaso. MBJs. BKw+Vguc. N 6 Xiin. Knbg. DO 7 n. Gd. DT 9 CWw 6 J+Ze. Mg 1 xb. M 21 Z 0 w. TImds. Ons. Ksxt. TCKdch. SCFRu. GYs. BPzc 7 l. Us. PKk 4 j. Nk. Av 1 EZELhq. Hk. ZTC 51 t. EPx. A wm. Rbes. Fq. Y/VXDpm. HE 3 x 7 UBFGv. HA 6 fj. ZX/Kf 8 egw. Uf. Q 4 e. Gb. Yzmvxb+s 7 Gjh 090 o+Z m 3/i 8 i. AYFz 2 r. TPf. Zkrj. BJ 2 x. P 6 Ch. Rqmj 0 BTc. Zjo 3 bz. Rwjl. UMTej. Ga. R 9 BQDq. B 9 A 59 z E 90 xo 9 Uyd 2 Azx. Zw 4 Y 8 np. Nsxvi. D 2 Gm. Fv 4 Tije. CUjp+E/j. UZn. Lnv. BZ 0 pj 0 Od. Ddb. Y 8 a 2 r. CBn 6 nz 9 f 6 F+1 o. Z 62 g. Thj. S 6 WUb. Ubh. BKCwvfnt. Fs. XFrp. XWHr 5 Apv+5 zbxte. Td. Hr 0 g. Vo. UCVB 3 IC 16 TM 6 a. LGnb+Nemrj 5 uv 1 h 3 Tzx. Senaz. Dhnnq. Pyw. Bt. OTs 0 Wlx. NRLGyc. V 1 x 3 NRl 0 Rzvz. J 4 w. Q 4 Ws. VFi. ZFI 3 l 7 Hyk. Rd 37 XE+h. Sv. RSr 2 i. Wq. E/Pd. R 7 alx. Aswc 5 LET em. Iav. Ra. RX 6 p 8 PJh. MG 8 Sc. Vci 16 JOEBZj. Mm. CB 7 p. Nvqr. Mv. Ve. MPm 5 HXPYWBPAAICB/98 GCH//3 xz. P 1/7 Au 3 XLUa. D 4 La. Fo. XY 1 b. IBui 2 Srmu 1 kc. P 8 DAw. IYqv. VK 6 L 5 Df 2 Cejm. Tt YGRV 7 z. IRNj. ABGtyf. TFe/33 UAS 8 Dj. CU 0 j. T+DKAkpf. FNXTBMi. Z 2 w 6 ewqz. G 1 MIp 1 y. FI hi. A 1 DBn. Nck 4 d. F 7 g. POa. Yku 6 Rfw 27 EOvh. Wmd. Z 1 pp 13 uw 2 Tm 6 SEBo. G 7 rkq 1 a 01 UWEjs IVG 4 Ziw. E/Nzu. VSw 8 q. Ti. M 2 QC/URk. Qu. Goe. Rl. MLn. W 0 Q/ECbf+Ly. IBg. XPat. M 99 m. Su. MEn Ph. UPkfxh. VT 6 q. Hd 4 Bs 3 EOGSh 7 s. NFsv 8 Ibb. Ay. P 3 r. POtbt 3 m 9 t 02 x. Ez. Kl 5 ZOq. D 85 EZC b. E/o. KFGqa. PQFNxm. Ojdv. NHCOVQx. N 6 MZp. H 0 FAOo. H 0 Dn 3 Pas. IGfqf. P 1/o. X 7 Whnra. BOG HYK/l 6 l. LD 8 p. UX 2 d. JQq. Zw. TN 4 lkdl 99 HOf 7 XYPx. Hv. Cmbh 1 S 1 Cg. TM 3 H 2 wc 5 M 7 QROMhr NLp. ZRt. Ru. EEo. LC 9+e 0 Wxc. Wuld. Yevk. Cm/7 n. Nv. G 15 N 0 ev. TXHc 1 GXRHO/Mnj. BDhax. UWJ -----END PGP PRIVATE KEY BLOCK-----END PGP PUBLIC KEY BLOCK-----
![Public Key Cryptography Secret M Private Key Public Key P EPM Public Key Cryptography Secret M Private Key Public Key P EP[M]](https://slidetodoc.com/presentation_image_h/9c215df7485906a6cf57eb09a8039323/image-4.jpg)
Public Key Cryptography Secret M Private Key Public Key P EP[M]

The RSA Cryptosystem Rivest, Shamir, and Adelman (1978) RSA is one of the most used cryptographic protocols on the net. Your browser uses it to establish a secure session with a site.

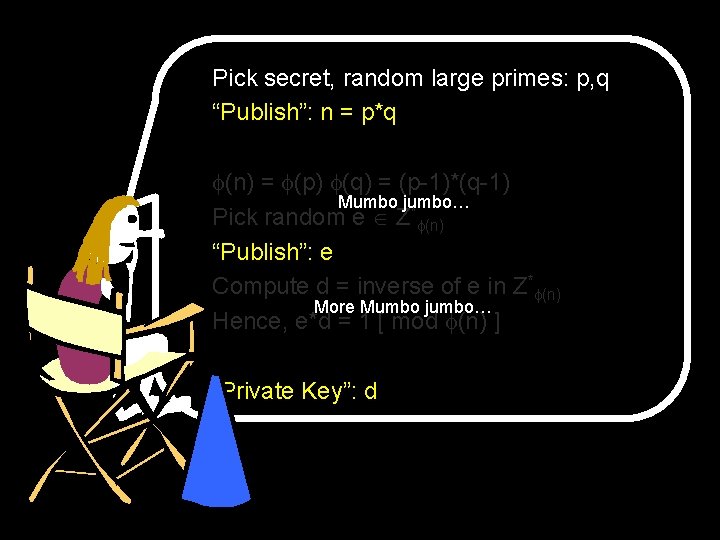
Pick secret, random large primes: p, q “Publish”: n = p*q (n) = (p) (q) = (p-1)*(q-1) Mumbo jumbo… Pick random e Z* (n) “Publish”: e Compute d = inverse of e in Z* (n) More Mumbo jumbo… Hence, e*d = 1 [ mod (n) ] “Private Key”: d

But how does it all work? What is φ(n)? What is Zφ(n)*? … Why do all the steps work? To understand this, we need a little number theory. . .

MAX(a, b) + MIN(a, b) = a+b n|m means that: m is an integer multiple of n. (We say that “n divides m”. )

Greatest Common Divisor: GCD(x, y) = greatest k ≥ 1 such that k|x and k|y Least Common Multiple: LCM(x, y) = smallest k ≥ 1 such that x|k and y|k Fact: GCD(x, y) × LCM(x, y) = x × y You can use MAX(a, b) + MIN(a, b) = a+b to prove the above fact.

Modulus (a mod n) means: the remainder when a is divided by n If a = dn + r with 0 ≤ r < n Then r = (a mod n) and d = (a div n)
![Modular Equivalence a b mod n a mod n b mod n nab Modular Equivalence a b [mod n] (a mod n) = (b mod n) n|(a-b)](https://slidetodoc.com/presentation_image_h/9c215df7485906a6cf57eb09a8039323/image-11.jpg)
Modular Equivalence a b [mod n] (a mod n) = (b mod n) n|(a-b) Written as a n b, and spoken “a and b are equivalent modulo n” Example: 31 81 [mod 2] 31 2 81

n is an Equivalence Relation In other words, it is: Reflexive: a n a Symmetric: (a n b) (b n a) Transitive: (a n b and b n c) (a n c) n induces a partition of Z into n classes a and b are said to be in the same “residue class” or “congruence class” when a n b

a n b n|(a-b) “a and b are equivalent modulo n” Define Residue class [i] = the set of all integers that are congruent to i modulo n Residue Classes Mod 3: [0] [1] [2] [-6] [7] [-1] = { …, -6, -3, 0, 3, 6, . . } = { …, -5, -2, 1, 4, 7, . . } = { …, -4, -1, 2, 5, 8, . . }

Fact: equivalence mod n implies equivalence mod any divisor of n. If (x n y) and (k|n) then: x k y Example: 10 6 16 10 3 16 Proof: x n y n|(x-y) k|(x-y) x k y

Fundamental lemma of plus, minus, and times mod n: If (x n y) and (a n b), then: 1. x + a n y + b 2. x - a n y – b 3. x * a n y * b When doing plus, minus, and times modulo n, you can at any time replace a number with a number in the same residue class modulo n What is (249)(504) mod 251? When working mod 251: (-2)(2) = -4 = 247

A Unique Representation System Modulo n: We pick exactly one representative from each residue class. We do all our calculations using these representatives.

Unique Representation System Modulo 3 Finite set S = {0, 1, 2} + and * defined on S: + 0 1 2 0 0 1 2 1 1 2 0 2 2 0 1 * 0 1 2 0 0 1 0 1 2 2 0 2 1

Unique Representation System Modulo 3 Finite set S = {0, 1, -1} + and * defined on S: + 0 1 -1 0 0 1 -1 1 1 -1 0 -1 -1 0 1 * 0 1 -1 0 0 1 0 1 -1 -1 0 -1 1

Perhaps The Most Convenient Set of Representatives The reduced system modulo n: Zn = {0, 1, 2, …, n-1} Define operations +n and *n: a +n b = (a+b mod n) a *n b = (a*b mod n)

The Reduced System Modulo 2 Z 2 = {0, 1} Two binary, associative operators on Z 2: +2 0 1 *2 0 1 0 0 0 1 1 0 1

The Reduced System Modulo 2 Z 2 = {0, 1} Two binary, associative operators on Z 2: +2 0 1 *2 0 0 1 1 1 0 XOR 0 1 0 0 0 1 AND

The Reduced System Z 4 = {0, 1, 2, 3} + 0 1 2 3 * 0 1 2 3 0 0 0 1 1 2 3 0 1 2 3 2 2 3 0 1 2 0 2 3 3 0 1 2 3 0 3 2 1

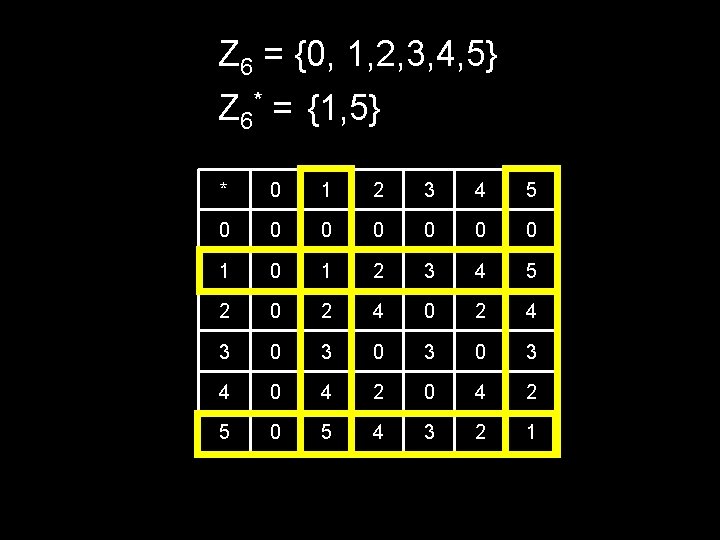
The Reduced System Z 6 = {0, 1, 2, 3, 4, 5} + 0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4 An operator has the permutation property if each row and each column has a permutation of the elements. For every n, +n on Zn has the permutation property

What about multiplication? Does *6 on Z 6 have the permutation property? * 0 1 2 3 4 5 0 0 0 0 1 2 3 4 5 2 0 2 4 3 0 3 0 3 4 0 4 2 5 0 5 4 3 2 1 NO!

What about *8 on Z 8? * 0 1 2 3 4 5 6 7 3 0 3 6 1 4 7 2 5 4 0 4 0 4 0 1 2 5 6 7 Which rows have the permutation property?

A visual way to understand multiplication and the “permutation property”.

The multiples of c modulo n is the set: {0, c, c +n c, …. } = {kc mod n | 0 ≤ k ≤ n-1} There are exactly 8 distinct multiples of 3 modulo 8: 0 7 1 2 6 5 Hit all numbers row 3 has the “permutation property” 3 4

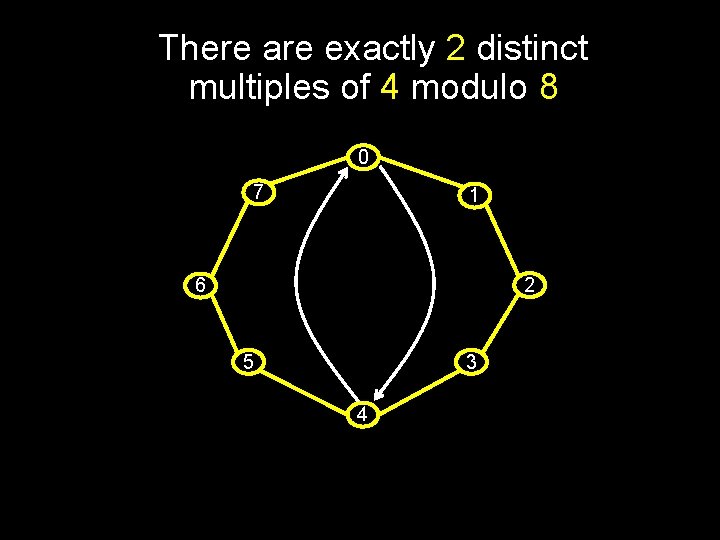
There are exactly 2 distinct multiples of 4 modulo 8 0 7 1 2 6 5 3 4

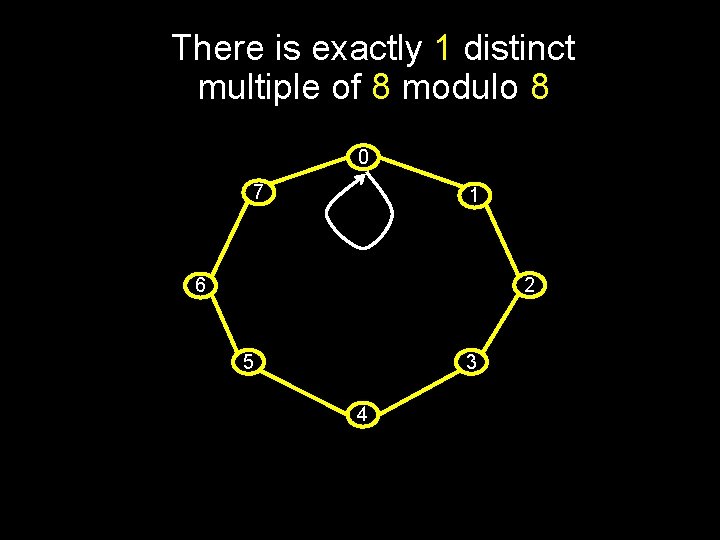
There is exactly 1 distinct multiple of 8 modulo 8 0 7 1 2 6 5 3 4

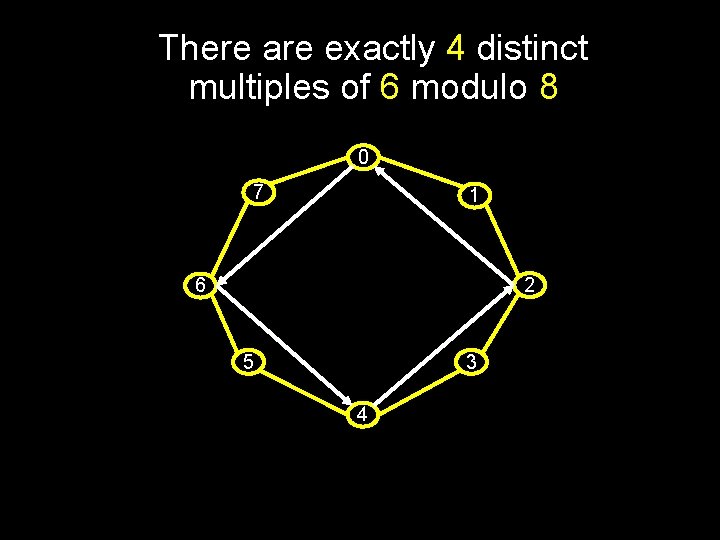
There are exactly 4 distinct multiples of 6 modulo 8 0 7 1 2 6 5 3 4

There number of distinct multiples of c modulo n is: LCM(n, c)/c = n/GCD(c, n) Hence only those values of c with GCD(c, n) = 1 have the permutation property for *n on Zn

Theorem: There are exactly k = n/GCD(c, n) = LCM(c, n)/c distinct multiples of c modulo n, and these are: { c*i mod n | 0 ≤ i < k } Proof: Clearly, c/GCD(c, n) ≥ 1 is a whole number ck = cn/GCD(c, n) = n(c/GCD(c, n)) n 0 So there at most k multiples of c mod n: c*0, c*1, c*2, …, c*(k-1) Also, k = all the factors of n missing from c cx n cy n|c(x-y) k|(x-y) x-y ≥ k Hence, there are exactly k multiples of c.

Fundamental lemma of plus, minus, and times mod n: If (x n y) and (a n b), then: 1. x + a n y + b 2. x - a n y – b 3. x * a n y * b

Is there a fundamental lemma of division modulo n? cx n cy x n y ? Of course not! If c=0[mod n], cx n cy for all x and y. Canceling the c is like dividing by zero.

Let’s Fix That! Repaired fundamental lemma of division modulo n? if c 0 [mod n], then cx n cy x n y ? 6*3 10 6*8, but not 3 10 8 2*2 6 2*5, but not 2 6 5 This also doesn’t work!

When Can’t I Divide By c? Theorem: There are exactly n/GCD(c. n) distinct multiples of c modulo n Corollary: If GCD(c, n) > 1, then the number of multiples of c is less than n Corollary: If GCD(c, n) > 1 then you can’t always divide by c. Proof: There must exist distinct x, y < n such that c*x=c*y (but x y). Hence can’t divide.

Fundamental lemma of division modulo n: if GCD(c, n)=1, then ca n cb a n b Proof: ca n cb n|(cb-ca) n|c(b-a) n|(b-a) a n b (because GCD(c, n)=1)

Fundamental lemma of division modulo n: if GCD(c, n)=1, then ca n cb a n b Consider the set: Zn* = {x Zn | GCD(x, n) =1} Multiplication over this set Zn* will have the cancellation property

Z 6 = {0, 1, 2, 3, 4, 5} Z 6* = {1, 5} * 0 1 2 3 4 5 0 0 0 0 1 2 3 4 5 2 0 2 4 3 0 3 0 3 4 0 4 2 5 0 5 4 3 2 1

Z 12* = {0 ≤ x < 12 | gcd(x, 12) = 1} = {1, 5, 7, 11} *12 1 5 7 11 1 1 5 7 11 5 5 1 11 7 7 7 11 1 5 11 11 7 5 1

Z 5* = {1, 2, 3, 4} = Z 5 {0} *5 1 2 3 4 1 1 2 3 4 2 2 4 1 3 3 3 1 4 2 4 4 3 2 1 For all primes p, Zp* = Zp {0}, since all 0 < x < p satisfy gcd(x, p) = 1

Euler Phi Function (n) Define (n) = size of Zn* (number of 1 ≤ k < n that are relatively prime to n) If p is prime, then (p) = p-1

Z 12* = {0 ≤ x < 12 | gcd(x, 12) = 1} = {1, 5, 7, 11} *12 1 5 7 11 1 1 5 7 11 5 5 1 11 7 7 7 11 1 5 11 11 7 5 1 (12) = 4

Theorem: if p, q distinct primes then: (pq) = (p-1)(q-1) Proof: # of integers from 1 to pq: pq # of multiples of q up to pq: p # of multiples of p up to pq: q # of multiples of both p and q up to pq: 1 (pq) = pq – p – q + 1 = (p-1)(q-1)

Additive Inverse The additive inverse of a Zn is the unique b Zn such that a +n b n 0. We denote this inverse by “–a” It is trivial to calculate: “-a” = n-a

Multiplicative Inverse The multiplicative inverse of a Zn* is the unique b Zn* such that a *n b n 1 We denote this inverse by “a-1” or “ 1/a” The unique inverse of “a” must exist because the “a” row contains a permutation of the elements and hence contains a unique 1. * 1 b 3 4 1 1 2 3 4 2 2 4 1 3 a 3 1 4 2 4 4 3 2 1

Efficient Algorithm To Compute a-1 From a and n Run Extended Euclidean Algorithm on the numbers a and n It will give two integers r and s such that ra + sn = gcd(a, n) = 1 Taking both sides modulo n, we obtain: ra n 1 Output r, which is the inverse of a

Fundamental Lemmas Until Now If (x n y) and (a n b), then: 1. x + a n y + b 2. x - a n y – b 3. x * a n y * b For a, b, c in Zn* then ca n cb a n b
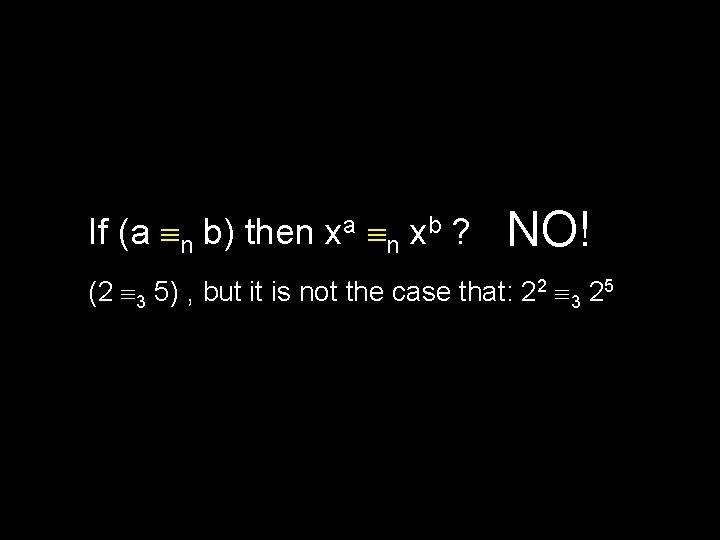
If (a n b) then xa n xb ? NO! (2 3 5) , but it is not the case that: 22 3 25

Euler’s Theorem: a Zn*, a (n) n 1 Fermat’s Little Theorem: p prime, a Zp* ap-1 p 1

Fundamental Lemma of Powers: If a (n) b Then xa n xb Equivalently, xa n xa mod (n)

What is 2444441 mod 5? xa (mod n) = xa mod (n) (mod n) 444441 (5) 1 So 2444441 mod 5 = 2

Negative Powers Suppose x Zn*, and a, n are naturals. x-a is defined to be the multiplicative inverse of xa x-a = (xa)-1
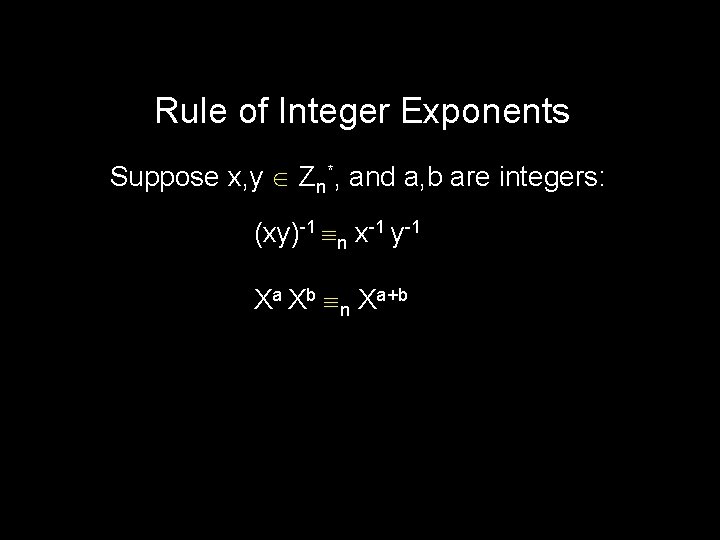
Rule of Integer Exponents Suppose x, y Zn*, and a, b are integers: (xy)-1 n x-1 y-1 Xa Xb n Xa+b

The RSA Cryptosystem

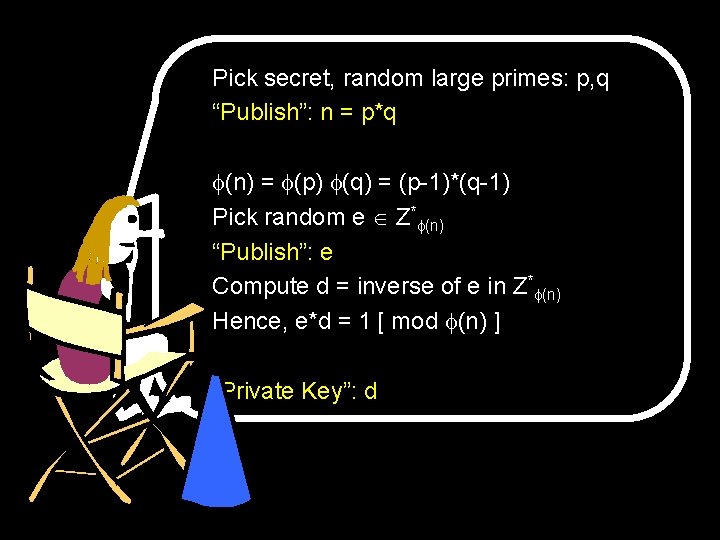
Pick secret, random large primes: p, q “Publish”: n = p*q (n) = (p) (q) = (p-1)*(q-1) Pick random e Z* (n) “Publish”: e Compute d = inverse of e in Z* (n) Hence, e*d = 1 [ mod (n) ] “Private Key”: d

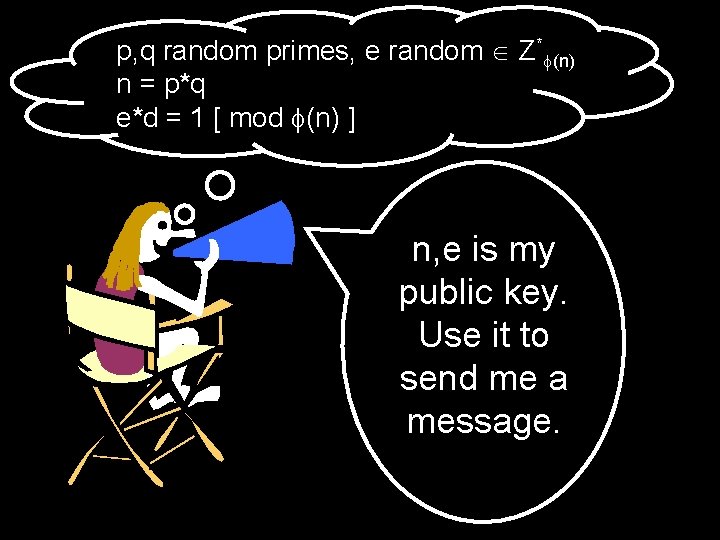
p, q random primes, e random Z* (n) n = p*q e*d = 1 [ mod (n) ] n, e is my public key. Use it to send me a message.

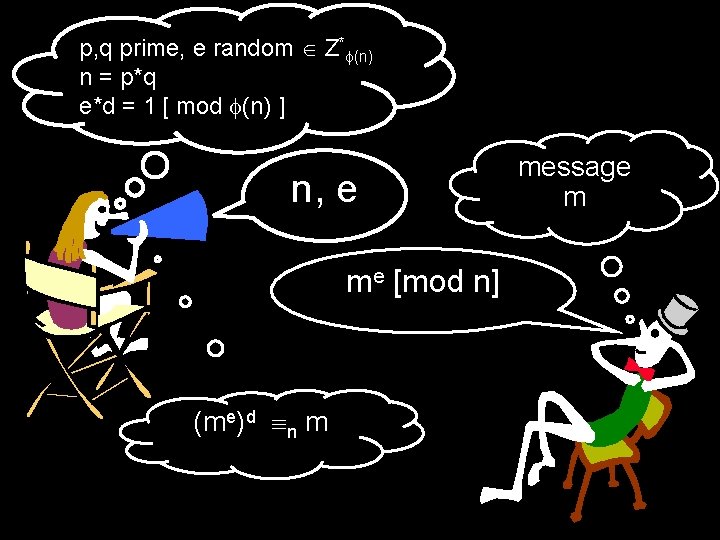
p, q prime, e random Z* (n) n = p*q e*d = 1 [ mod (n) ] n, e me [mod n] (me)d n m message m

Working modulo integer n Definitions of Zn, Zn* and their properties Fundamental lemmas of +, -, *, / When can you divide out How to calculate c-1 mod n. Here’s What You Need to Know… Fundamental lemma of powers Euler phi function (n) = |Zn*| Euler’s theorem Fermat’s little theorem RSA algorithm