15 251 Some AWESOME Great Theoretical Ideas in






















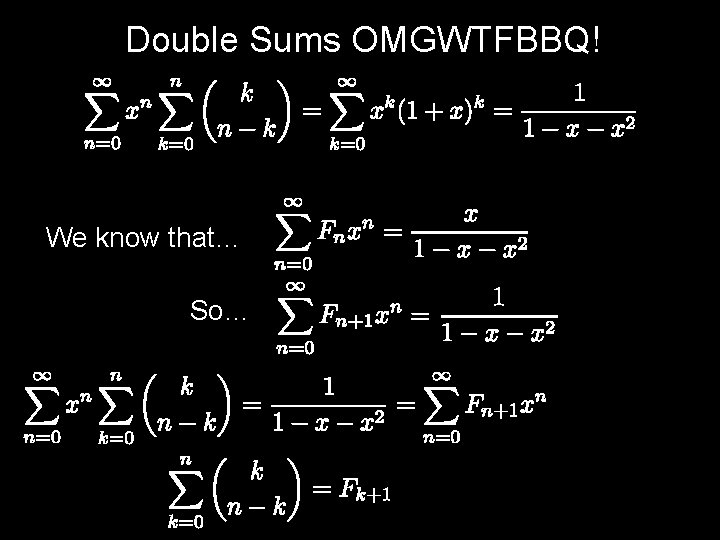






- Slides: 35

15 -251 Some AWESOME Great Theoretical Ideas in Computer Science about Generating Functions

MORE Generating Functions Lecture 7 (February 2, 2010) Adam Blank

Announcements You are now breathing manually Homework 3 is due tonight • Please submit a collaborators graph again. • It doesn’t matter what you name it. • You do not also have to list your collaborators in the pdf Homework 4 is out • This assignment is non-trivial • Start early! Exam 1 will be in recitation next week • Don’t be late! • We will (tentatively) have a review session on Saturday • We will email you with updates

What good are Generating Functions anyway?

What good are Generating Functions anyway? They're fun! Solving recurrences precisely They are often easier than the alternative!

Some Terminology Closed form of a Generating Function Closed form for a Recurrence

Let’s do some problems!

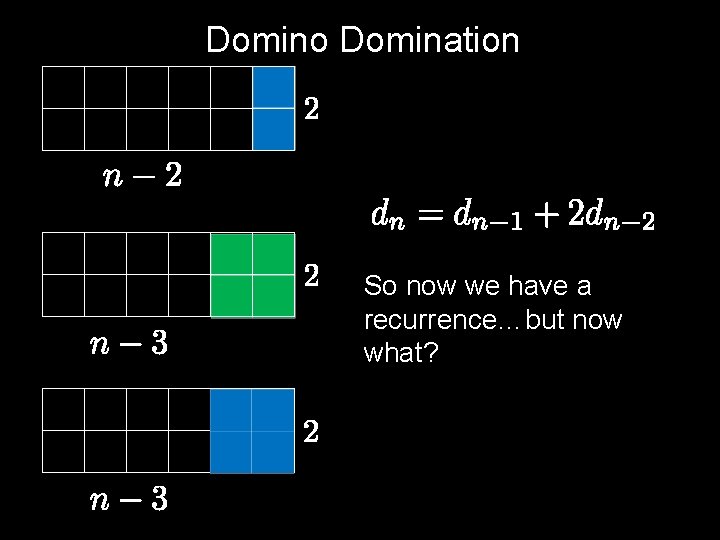
Domino Domination We have a board, and we would like to fill it with dominos. We have two colors of dominos: green and blue. The green ones must be used in pairs (so that they don’t get blue!), and they must be vertical. How many ways can we tile our board?

Domino Domination We have a board, and we would like to fill it with dominos. We have two colors of dominos: green and blue. The green ones must be used in pairs (so that they don’t get blue!), and This is a combinatorial question! they must be vertical. How many ways can we tile How should we proceed? !? ! our board? Write a recurrence!

Domino Domination So now we have a recurrence…but now what?

Domino Domination Now we derive a closed form using generating functions! Let We know the base cases: Note that these base cases are actually correct. is the number of ways to tile a board.

Domino Domination Now we derive a closed form using generating functions! Let

Domino Domination Now we derive a closed form using generating functions! Let

Domino Domination Now we have a closed form for the generating function! …what now? Let

Domino Domination Now we have a closed form for the generating function! …what now? Let

Domino Domination Now we have a closed form for the generating function! …what now? Let

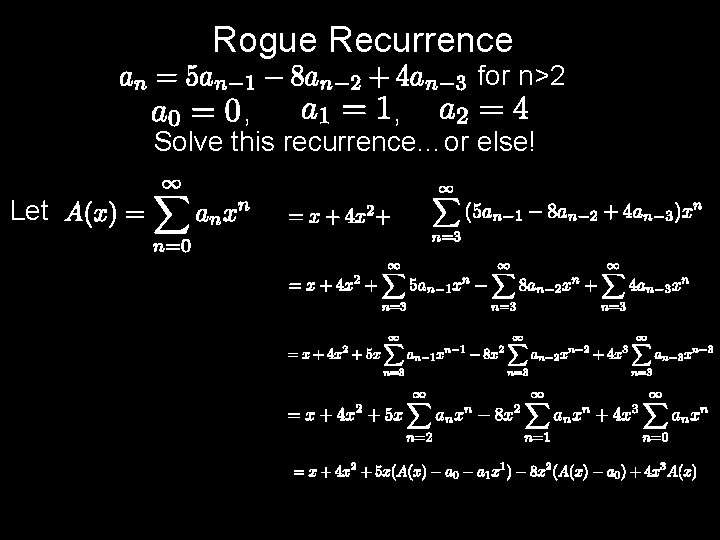
Rogue Recurrence for n>2 , , Solve this recurrence…or else! Let

Rogue Recurrence for n>2 , , Solve this recurrence…or else! Let

Rogue Recurrence for n>2 , , Solve this recurrence…or else! Let

Rogue Recurrence for n>2 , , Solve this recurrence…or else! Let What next? Partial fractions?

Rogue Recurrence No. Let’s be sneaky instead!

Rogue Recurrence for n>2 , , Now back to the recurrence… Let

Double Sums OMGWTFBBQ! Let’s revisit the last lecture… We would like to swap the summations. All we have done here is re-group the addition.

Double Sums OMGWTFBBQ! We know that…
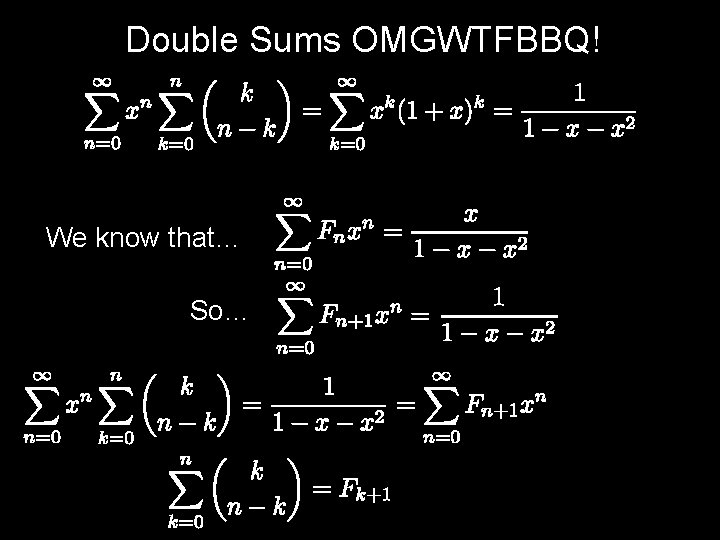
Double Sums OMGWTFBBQ! We know that… So…

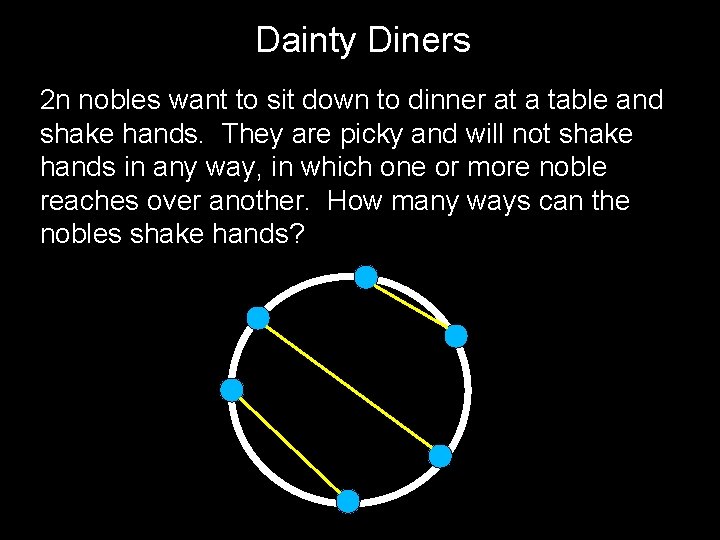
Dainty Diners 2 n nobles want to sit down to dinner at a table and shake hands. They are picky and will not shake hands in any way, in which one or more noble reaches over another. How many ways can the nobles shake hands?

Dainty Diners Look at an arbitrary person, and think about who he could shake hands with.

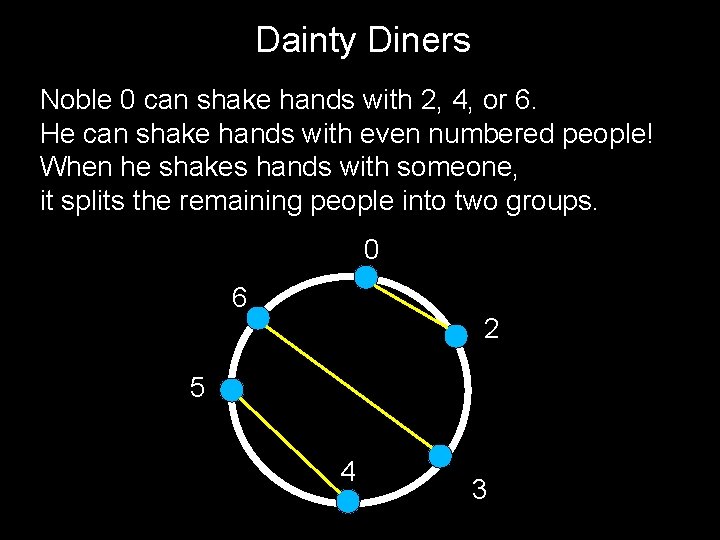
Dainty Diners Noble 0 can shake hands with 2, 4, or 6. He can shake hands with even numbered people! When he shakes hands with someone, it splits the remaining people into two groups. 0 6 2 5 4 3

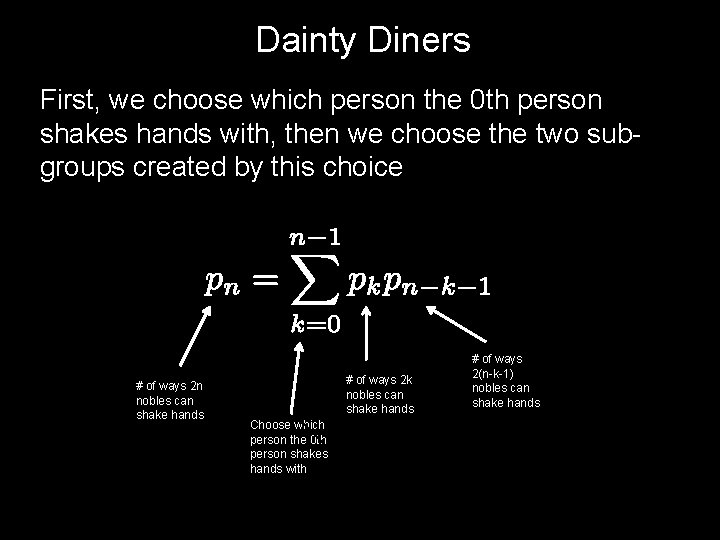
Dainty Diners First, we choose which person the 0 th person shakes hands with, then we choose the two subgroups created by this choice # of ways 2 n nobles can shake hands # of ways 2 k nobles can shake hands Choose which person the 0 th person shakes hands with # of ways 2(n-k-1) nobles can shake hands

Dainty Diners n=1: n>1: Let

Dainty Diners What now? Our usual trick of putting the terms in terms of P(x) doesn’t seem to be possible!

Dainty Diners Idea! Isolate the double summation and list out some terms. Is there a pattern? ?

Dainty Diners Let C(x) be an arbitrary generating function! Suppose we take k terms from the left. We need n-k from the second to make n total powers of k.

Dainty Diners After some “magic” (see Newton’s Binomial Theorem):

Generating Functions • How to solve recurrences • Summation techniques • Simple partial fractions • Simple differentiation Here’s What You Need to Know… (mostly remember how to use generating functions to solve recurrences)
 Great theoretical ideas in computer science
Great theoretical ideas in computer science Great ideas in theoretical computer science
Great ideas in theoretical computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Steven rudich
Steven rudich Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science 15-251
15-251 Stanford cs 251
Stanford cs 251 Cs 251 stanford
Cs 251 stanford Half lap muff coupling drawing
Half lap muff coupling drawing Aae 251 purdue
Aae 251 purdue 15-251
15-251 Stanford cs 251
Stanford cs 251 Legge 251 del 2000 art 1
Legge 251 del 2000 art 1 Cs 251
Cs 251 Hino a vida tem tristezas mil
Hino a vida tem tristezas mil Amedd enlisted commissioning program
Amedd enlisted commissioning program Awesome sql
Awesome sql Awesome god medley
Awesome god medley Awesome power of prayer
Awesome power of prayer Our god is an awesome god vine
Our god is an awesome god vine We will celebrate our god lyrics
We will celebrate our god lyrics Awesome chinese song
Awesome chinese song Awesome mongodb
Awesome mongodb Kahoot makes learning awesome
Kahoot makes learning awesome Syntactically awesome stylesheets
Syntactically awesome stylesheets Awesome adverbs
Awesome adverbs Culture shock germany
Culture shock germany Comparative irregular adjectives
Comparative irregular adjectives Our god is an awesome god
Our god is an awesome god God is awesome quotes
God is awesome quotes Proclaim your awesome power
Proclaim your awesome power