Visualization Chapter 12 CS 480680 Chapter 12 Visualization

Visualization Chapter 12 CS 480/680 Chapter 12 -- Visualization

n Introduction: n n In this chapter, we apply almost everything we have done so far to the problem of visualizing large data sets that arise in scientific and medical applications. Fortunately, we can bring many tools to bear on these problems n n n CS 480/680 We can create geometric objects We can color them, animate them, or change their orientation. With all these possibilities, and others, there are multiple ways to visualize a given data set, and we will explore some of the possibilities in this chapter. Chapter 12 -- Visualization 2

1. Data + Geometry n Data comprise numbers. n They are not geometric objects and thus they cannot be displayed directly by our graphics systems. n Only when we combine data with geometry are we able to create a display and to visualize the underlying information. n A simple definition of (scientific) visualization is: n the merging of data with the display of geometric objects through computer graphics CS 480/680 Chapter 12 -- Visualization 3

n We consider three types of problems: n scalar visualization: n we are given a three-dimensional volume of scalars, such as X-ray densities. n vector visualization: n we start with a volume of vector data, such as the velocity at each point in a fluid n tensor visualization: n we have a matrix of data at each point, such as the stresses within a mechanical part. CS 480/680 Chapter 12 -- Visualization 4

n We must confront several difficulties n One is the large size of the data sets. CS 480/680 n Many of the most interesting applications involve data that are measured over three spatial dimensions and often also in time. n For example, the medical data such as from an MRI can be at a resolution of 512 x 200 points. n The visible-woman data set is a volume of densities that consist of 1734 x 512 data points. n consequently, we cannot assume that any operation on our data, no matter how conceptually simple it appears, can be carried out easily Chapter 12 -- Visualization 5

n Second, these data are only data n n They are not geometric objects Thus we must translate these data to create and manipulate geometric objects. n Third, we may have multidimensional data points CS 480/680 n For example, n When we measure the flow of a fluid at a point, we are measuring the velocity, a three-dimensional quantity. n When we measure the stress or strain on a solid body at some internal point, we collect a 3 x 3 matrix of data. n How we convert these data to geometric objects and select the attributes of those objects determines the variety of visualization strategies. Chapter 12 -- Visualization 6

2. Height Fields and Contours n One of the most basic and important tasks in visualization is visualizing the structure in a mathematical function. n This problem arises in many forms, the biggest difference is n how we are given the function n implicitly, explicitly, or parametrically. n And in how many independent variables define the function. CS 480/680 Chapter 12 -- Visualization 7

n In this section, we consider two problems that lead to similar visualization methods n One is the visualization of an explicit function of the form: n z = f(x, y) with two dependent variables n Such functions are sometimes called height fields n CS 480/680 Chapter 12 -- Visualization 8

n The second form is an implicit function in two variables: g(x, y) = c where c is a constant. n n CS 480/680 This equation describes one or more two-dimensional curves in the x, y plane. There may also be no x, y values that satisfy the equation. This curve is called the contour curve, corresponding to c Chapter 12 -- Visualization 9

n 2. 1 Meshes n The most common method to display a function f(x, y) is to draw a surface. n If the function f is known only discretely, then we have a set of samples or measurements of experimental data of the form: n zij = f(xi, yj) n We assume that the data are evenly spaced. n If f is known analytically, then we can sample it to obtain a set of discrete data with which to work. CS 480/680 Chapter 12 -- Visualization 10

n One simple way to generate a surface is through either a triangular or a quadrilateral mesh. n Thus the data define a mesh of either n n NM quadrilaterals or 2 NM triangles. n The corresponding Open. GL programs are simple. n The following figure shows a rectangular mesh from height data for a part of Honolulu, Hawaii CS 480/680 Chapter 12 -- Visualization 11

n There are interesting aspects to and modifications we can make to the Open. GL program n First, if we use all the data, the resulting plot may contain many small polygons CS 480/680 n The resulting line density may be annoying and can lead to moiré patterns n Hence we might prefer to sub-sample the data n use every kth point for some k n or by averaging groups of data to obtain a new set of samples with smaller N and M. Chapter 12 -- Visualization 12

n Second, the figure we saw was drawn with both black lines and white filled polygons. n The lines are necessary to display the mesh. n The polygons are necessary to hide data behind the mesh. n If we display the data by first drawing the polygons in back and then proceed towards the front, the front polygons automatically hide the polygons further back. n n CS 480/680 Since the data is well-structured, this is possible. If hidden surface removal is done in software, this might be faster than turning on z-buffering. Chapter 12 -- Visualization 13

n There is one additional trick that we used to display this figure. n If we draw both a polygon and a line loop with the same data, such as: n n n n n CS 480/680 glcolor 3 f(1. 0, 1. 0); gl. Begin(GL_QUADS). . . gl. Vertex 3 i(. . . ) gl. End(); gl. Color 3 f(0. 0, 0. 0); gl. Begin(GL_LINE_LOOP); . . . gl. Vertex 3 i(. . . ) gl. End(); then the polygon and the line loop are in the same plane. Chapter 12 -- Visualization 14

CS 480/680 n Even though the line loop is rendered after the polygon, numerical inaccuracies in the renderer often cause part of the line loop to be blocked by the polygon. n We can enable the polygon offset mode and se the offset parameter as in: n gl. Enable(GL_POLYGON_OFFSET_FIL) n gl. Polygon. Offset(1. 0, 0. 5) n These functions move the lines slightly toward the viewer relative to the polygon, so all the desired lines are now visible. Chapter 12 -- Visualization 15

n The basic mesh plot can be extended in many ways. CS 480/680 n If we display only the polygons then we can add lighting to create a realistic image of a surface in mapping applications. n The required normals can be computed from the vertices of the triangles or quadrilaterals. n Another option is to map a texture to the surface n The texture map might be an image of the terrain from a photograph or other information that might be obtained by digitization of a map. n If we combine these techniques, we can generate a display in which, by changing the position of the light source, we can make the image depend on the time of day. Chapter 12 -- Visualization 16

n 2. 2 Contour Plots n One of the difficulties with mesh plots is that, although they give a visual impression of the data, it is difficult to make measurements from them. n An alternative method of displaying the height data is to display contours -- curves that correspond to a fixed value of height. n n n CS 480/680 We can use this method to construct topographic maps used by geologists and hikers. The use of contours is still important, both on its own and as part of other visualization techniques. We solve the accuracy problem of sampled data by using a technique called marching squares Chapter 12 -- Visualization 17

n 2. 3 Marching Squares n Suppose: n we have a function f(x, y) that we sample at evenly spaced points on a rectangular array (or lattice) in x and y. n that we would like to find an approximate contour curve n Our strategy is to construct a curve of connected line segments (piecewise linear) n CS 480/680 We start with a rectangular cell determined by four grid points Chapter 12 -- Visualization 18

n Our algorithm finds the line segments on a cellby-cell basis using only the values of z at the corners of the cell to determine whether the desired contour passes through the cell. n Consider this case CS 480/680 Chapter 12 -- Visualization 19

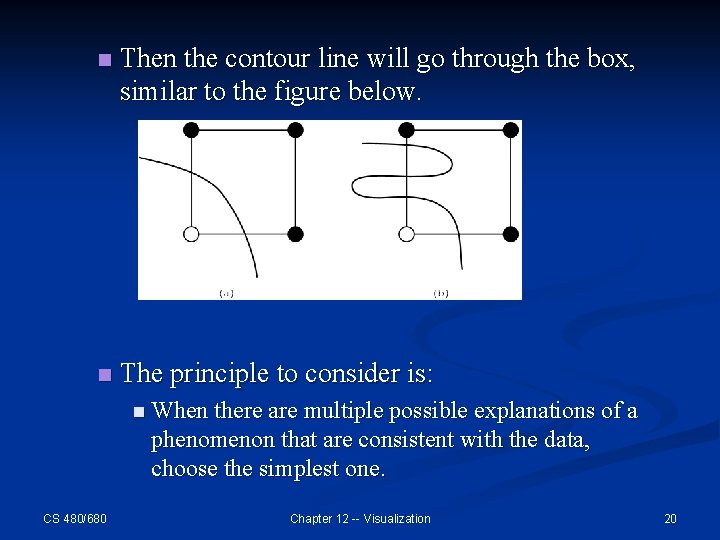
n Then the contour line will go through the box, similar to the figure below. n The principle to consider is: n When there are multiple possible explanations of a phenomenon that are consistent with the data, choose the simplest one. CS 480/680 Chapter 12 -- Visualization 20

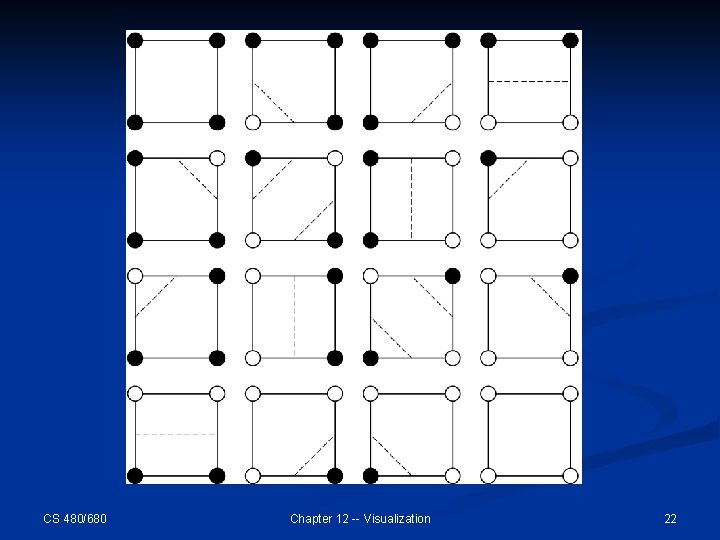
n Returning to our example: n We can now draw the line for this cell. The issue is where do we draw it? n n n Pick the mid point on each edge and connect them Interpolate the crossing points. There are 16 (24)ways that we can color the vertices of a cell using only black and white. n All could arise in our contour problem. n These cases are itemized on the next slide CS 480/680 Chapter 12 -- Visualization 21

CS 480/680 Chapter 12 -- Visualization 22

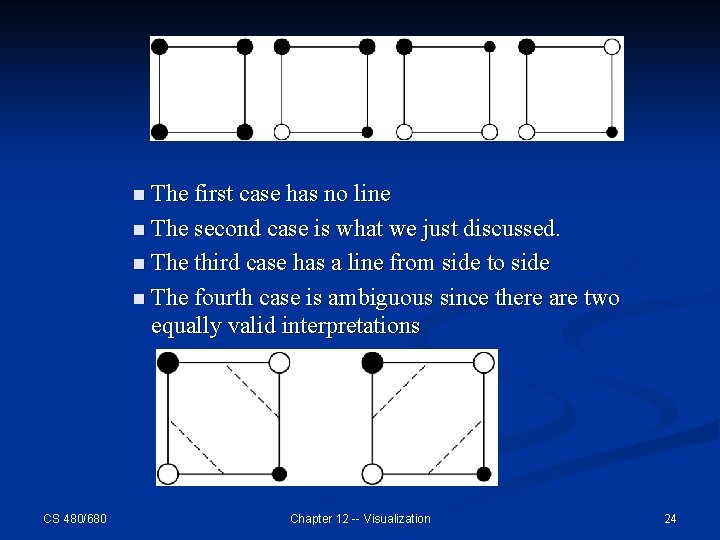
n If we study these cases, we see that there are two types of symmetry n Rotational (1 & 2) n Inverses (0 & 15) n Once we take symmetry into account, only 4 cases truly are unique: CS 480/680 Chapter 12 -- Visualization 23

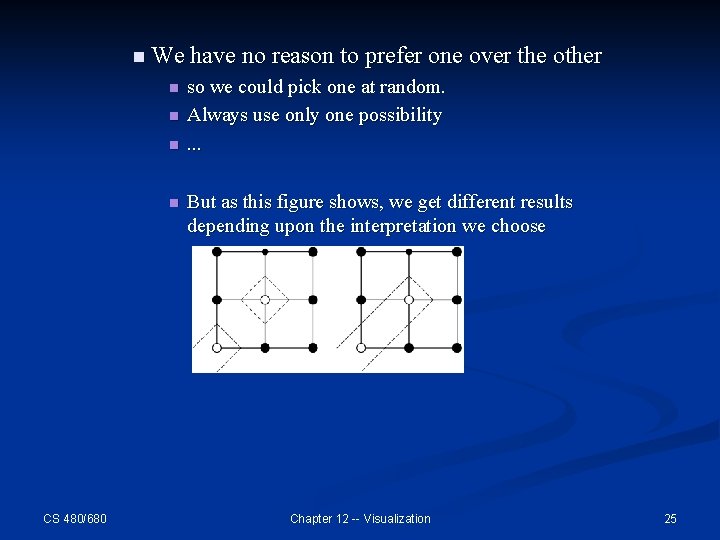
n The first case has no line n The second case is what we just discussed. n The third case has a line from side to side n The fourth case is ambiguous since there are two equally valid interpretations CS 480/680 Chapter 12 -- Visualization 24

n We have no reason to prefer one over the other n n CS 480/680 so we could pick one at random. Always use only one possibility. . . But as this figure shows, we get different results depending upon the interpretation we choose Chapter 12 -- Visualization 25

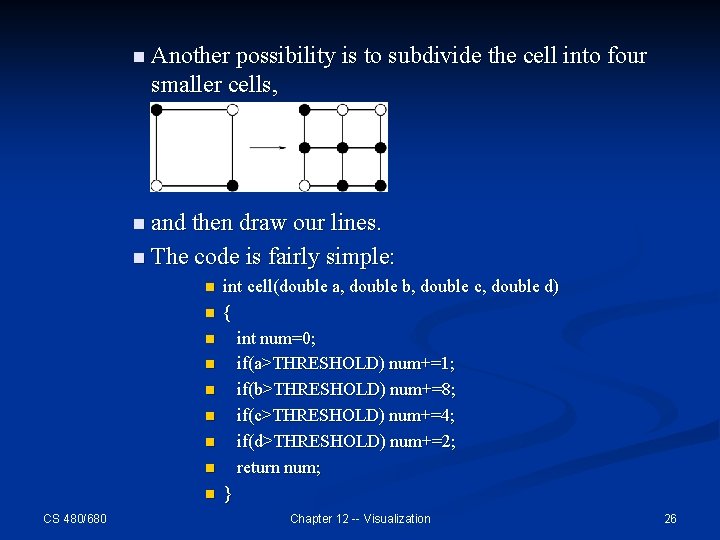
n Another possibility is to subdivide the cell into four smaller cells, n and then draw our lines. n The code is fairly simple: n n n n n CS 480/680 int cell(double a, double b, double c, double d) { int num=0; if(a>THRESHOLD) num+=1; if(b>THRESHOLD) num+=8; if(c>THRESHOLD) num+=4; if(d>THRESHOLD) num+=2; return num; } Chapter 12 -- Visualization 26

n We then can assign the cell to one of the four cases by: n n n n CS 480/680 switch(num){ case 1: case 2: case 4: case 7: case 8: case 11: case 13: case 14: draw_one(num, i, j, a, b, c, d); break; // contour cuts off one corner case 3: case 6: case 9: case 12: draw_adjacent(num, i, j, a, b, c, d); break; // contour crosses cell case 5: case 10: draw_opposite(num, i, j, a, b, c, d); break; // ambiguous case 0: case 15: break; // no contour in cell } Chapter 12 -- Visualization 27

n n n n n CS 480/680 n void draw_one(int num, int i, int j, double a, double b, double c, double d) { // compute the lower left corner of the cell and s_x and s_y here. switch(num){ case 1: case 14: x 1=ox; y 1 = oy+s_y; x 2= ox+s_x; y 2 = oy; break; /* the other cases go here case 2: case 13: . . . case 4: case 11: . . . Case 7: case 8: . . . } gl. Begin(GL_LINES); gl. Vertex 2 d(x 1, y 1); glvertex 2 d(x 2, y 2); gl. End(); Chapter 12 -- Visualization } 28

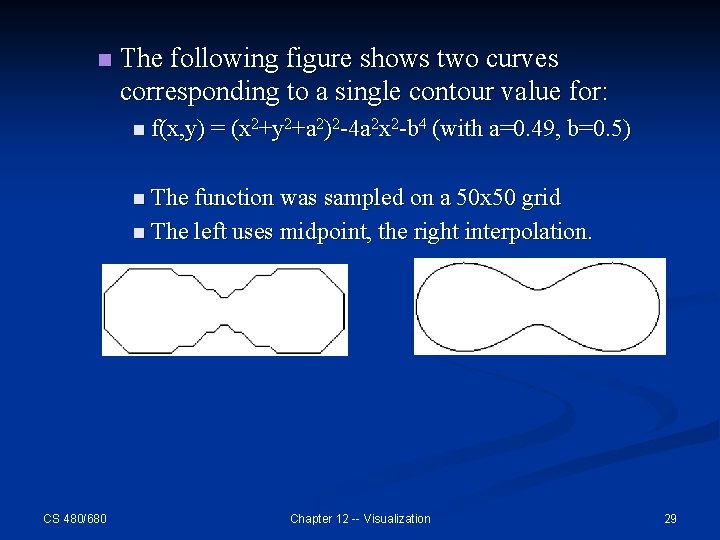
n The following figure shows two curves corresponding to a single contour value for: n f(x, y) = (x 2+y 2+a 2)2 -4 a 2 x 2 -b 4 (with a=0. 49, b=0. 5) n The function was sampled on a 50 x 50 grid n The left uses midpoint, the right interpolation. CS 480/680 Chapter 12 -- Visualization 29

n This next figure shows the Honolulu data set with equally spaced contours: n The Marching squares algorithm just described is nice because all the cells are independent. CS 480/680 Chapter 12 -- Visualization 30

3. Visualizing Surfaces and Scalar Fields n The surface and contour problems just described have three-dimensional extensions. n f(x, y, z) defines a scalar field. n An example is the density inside an object or the absorption of X-rays in the human body. CS 480/680 Chapter 12 -- Visualization 31

n Visualization of scalar fields is more difficult than the problems we have considered so far for two reasons: CS 480/680 n First, three-dimensional problems have more data with which we must work. n Consequently, operations that are routine for 2 D data (reading files and performing transformations) present practical difficulties. n Second, when we had a problem with two independent variables, we were able to use third dimension to visualize scalars. n When we have three, we lack the extra dimension to use for display. n Nevertheless, if we are careful, we can extend our previously developed methods to visualize threedimensional scalar fields Chapter 12 -- Visualization 32

n 3. 1 Volumetric Data Sets n Once again, assume that our samples are taken at equally spaced points in x, y, and z n The little boxes are called volume elements or voxels CS 480/680 Chapter 12 -- Visualization 33

n Even more so than for two-dimensional data, there are multiple ways to display these data sets. n However there are two basic approaches: n Direct Volume Rendering n makes use of every voxel in producing an image n Isosurfaces n CS 480/680 use only a subset of the voxels Chapter 12 -- Visualization 34

n 3. 2 Visualization of Implicit Functions n This is the natural extension of contours to 3 D n Consider the implicit function in three dimensions n g(x, y, z) = 0 where g is known analytically. n One way to attack this problem involves a simple form of ray tracing (ray casting) CS 480/680 Chapter 12 -- Visualization 35

n Finding isosurfaces usually involves working with a discretized version of the problem n replacing g by a set of samples taken over some grid. n CS 480/680 Our prime isosurface visualization method is called marching cubes, the three-dimensional version of marching squares. Chapter 12 -- Visualization 36

4. Isosurfaces and Marching Cubes n Assume that we have a data set, where each voxel is a sample of the scalar field f(x, y, z) n Eight adjacent grid points define a three-dimensional cell as shown here: CS 480/680 Chapter 12 -- Visualization 37

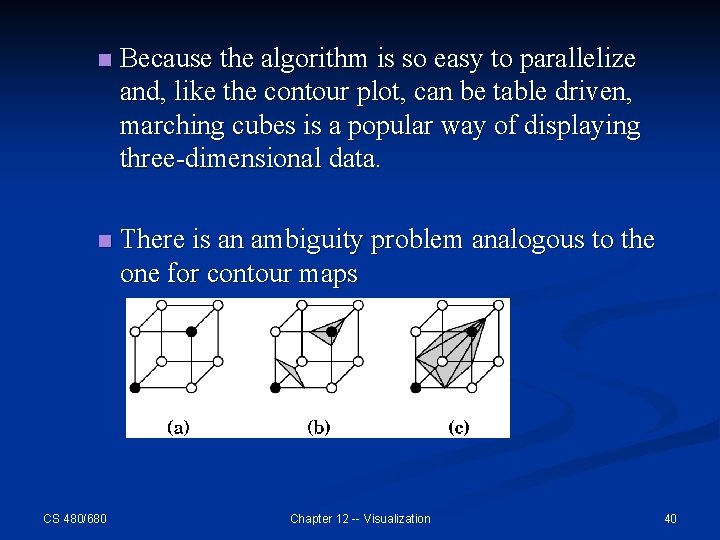
n We can now look for parts of isosurfaces that pass through these cells, based only on the values at the vertices. n There are 256=28 possible vertex colorings, but once we account for symmetries, there are only 14 unique cases CS 480/680 Chapter 12 -- Visualization 38

n Using the simplest interpretation of the data, we can generate the points of intersection between the surface and the edges of the cubes by linear interpolation. n Finally we can use the triangle polygons to tessellate these intersections. CS 480/680 Chapter 12 -- Visualization 39

n Because the algorithm is so easy to parallelize and, like the contour plot, can be table driven, marching cubes is a popular way of displaying three-dimensional data. n There is an ambiguity problem analogous to the one for contour maps CS 480/680 Chapter 12 -- Visualization 40

5. Mesh Simplification n On disadvantage of marching cubes is that the algorithm can generate many more triangles than are really needed to display the isosurface. One reason can be the resolution of the data set. n We can often create a new mesh with far fewer triangles such that the rendered surfaces are visually indistinguishable. n There are multiple approaches to this mesh simplification problem n CS 480/680 Chapter 12 -- Visualization 41

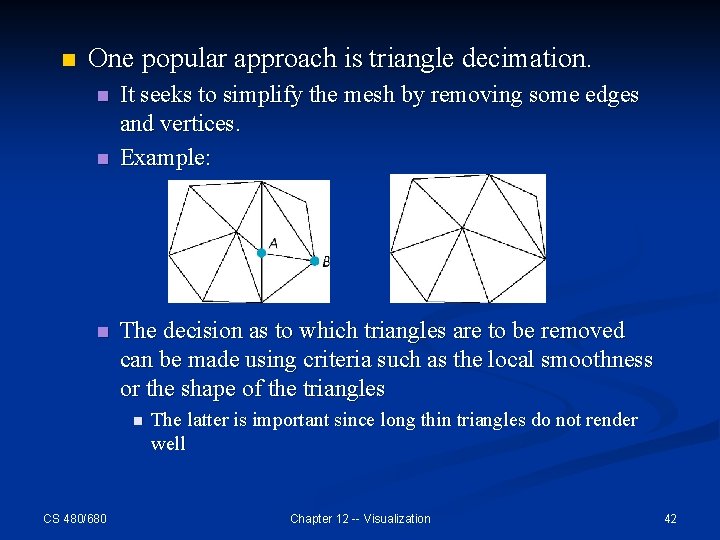
n One popular approach is triangle decimation. n n n It seeks to simplify the mesh by removing some edges and vertices. Example: The decision as to which triangles are to be removed can be made using criteria such as the local smoothness or the shape of the triangles n CS 480/680 The latter is important since long thin triangles do not render well Chapter 12 -- Visualization 42

Other approaches are based upon resampling the surface generated by the original mesh , thus creating a new surface n Probably the most popular technique is Delauney triangulation. n This algorithm creates a triangular mesh in which the circle determined by the vertices of each triangle contains no other vertices. n The complexity of this is O(n log n) n CS 480/680 Chapter 12 -- Visualization 43

6. Direct Volume Rendering n The weakness of isosurface rendering is that not all voxels contribute to the final image. n Consequently, we could miss the most important part of the data by selecting the wrong isovalue. n Direct volume rendering constructs images in which all voxels can make a contribution to the image. CS 480/680 Chapter 12 -- Visualization 44

n Early methods for direct volume rendering treated each voxel as a small cube that was either transparent or completely opaque. n These techniques produced images with serious aliasing artifacts. n CS 480/680 With the use of color and opacity, we can avoid or mitigate these problems. Chapter 12 -- Visualization 45

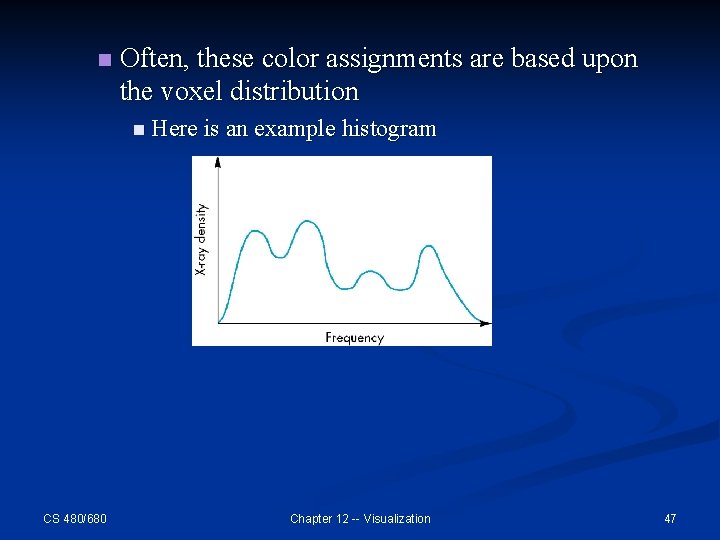
n 6. 1 Assignment of Color and Opacity n We start by assigning a color and transparency to each voxel. n If the data are from a computer-tomography scan of a person’s head, we might assign colors based upon the X-ray density. n n CS 480/680 Soft tissues (low density) might be red. Fatty tissues (medium densities) might be blue Hard tissues (high densities) might be white Empty space might be black. Chapter 12 -- Visualization 46

n Often, these color assignments are based upon the voxel distribution n Here is an example histogram CS 480/680 Chapter 12 -- Visualization 47

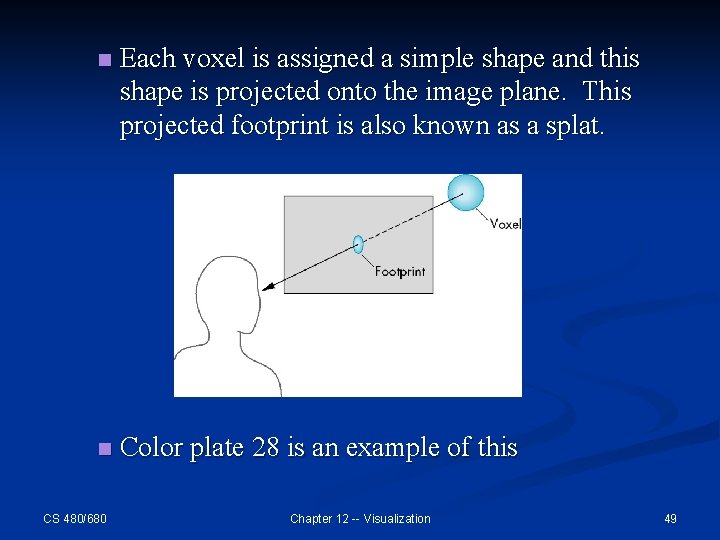
n 6. 2 Splatting n Once colors and opacities are assigned, , we can assign a geometric shape to each object. n Sometimes this is done with a back to front painting. n CS 480/680 Consider the voxels in the following figure Chapter 12 -- Visualization 48

n Each voxel is assigned a simple shape and this shape is projected onto the image plane. This projected footprint is also known as a splat. n Color plate 28 is an example of this CS 480/680 Chapter 12 -- Visualization 49

n 6. 3 Volume Ray Tracing n CS 480/680 An alternative direct-volume rendering technique is front-to-back rendering by raytracing. Chapter 12 -- Visualization 50

n 6. 4 Texture Mapping of Volumes n The importance of texture mapping in animation systems has led to the inclusion of large amounts of texture memory in recent graphics systems. n Once texture mapping is supported by the hardware, we can render scenes with texture mapping at almost the same rate as we can scenes without texture. n Three-dimensional texture rendering (which Open. GL supports) suggest a new approach to direct volume rendering. CS 480/680 Chapter 12 -- Visualization 51

7. Vector Field Visualization Our first visualization task considered a scalar field f(x, y, z) defined over a volume of space. n Now suppose that at each spatial point, we measure not a single value but rather a vector of n values. n n For example, in fluid-flow problems, we might measure the velocity at each point. n Our visualization techniques for three-dimensional vector fields employ two primary tools: n color and geometric objects. CS 480/680 Chapter 12 -- Visualization 52

n 7. 1 Hedgehogs n CS 480/680 Example: Blood flow visualization Chapter 12 -- Visualization 53

n 7. 2 Glyphs n CS 480/680 Example: flow visualization Chapter 12 -- Visualization 54

n 7. 3 Color n Sometimes called color quantization n Selection of a color for an intensity CS 480/680 Chapter 12 -- Visualization 55

n 7. 4 Particle Traces and Streamlines n CS 480/680 Typically used if computational fluid dynamics Chapter 12 -- Visualization 56

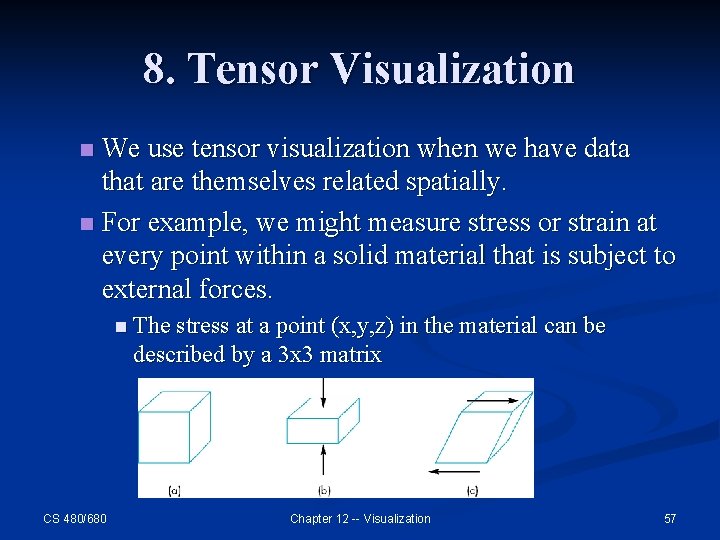
8. Tensor Visualization We use tensor visualization when we have data that are themselves related spatially. n For example, we might measure stress or strain at every point within a solid material that is subject to external forces. n n The stress at a point (x, y, z) in the material can be described by a 3 x 3 matrix CS 480/680 Chapter 12 -- Visualization 57

n One method of visualization is to display small cubes, each of which has been distorted by the local stress matrix. n Another method is to display properties of the matrix. n For example, if the matrix is symmetric then we can decompose it into its eigenvalues and eigenvectors n n CS 480/680 the eigenvalues are the most important characteristic of a matrix. Then you can associate an ellipsoid with the three eigenvalues n the eigenvalues determine the length of the three axes of the ellipse n the eigenvectors determine the orientation Chapter 12 -- Visualization 58

9. Summary n Although visualization encompasses everything we don in computer graphics, recent work in visualization has focused on the large data sets that arise in medical applications and from scientific simulations. n These data sets are so large that not only can they burden the best of hardware, but also conceptually simple operations (rendering, repositioning data) can be difficult. CS 480/680 Chapter 12 -- Visualization 59

n For volumetric data sets of scalars, we have introduced two general approaches: isosurfaces and volume rendering. n These techniques are fast and construct geometric objects that can be manipulated interactively. n Their weakness is that they do not make use of all the data. n Vector-visualization techniques are most important in flow visualization n Here we have sought to show patterns of flow through a variety of techniques including hedgehogs, glyphs, streamlines, and particle traces. CS 480/680 Chapter 12 -- Visualization 60

n For problems in which we have data of more than three dimensions at each point, including tensor visualization, it is less clear how we should visualize the information. n The difficulties are twofold n First, our graphics systems can display only three- dimensional primitives. n Second, although we can use other variables, such as color, to increase the “dimension” of the display, human observers may have difficulty interpreting such displays CS 480/680 Chapter 12 -- Visualization 61

10. Suggested Readings n The marching-squares method is a special case of the marching cubes method popularized by Lorenson and Kline (87) n This method has been rediscovered many times. n Early attempts to visualize volumes were reported by Herman (79) and by Fuchs (77) n Ray Tracing volumes was introduced in ‘ 88, Splatting in ‘ 90, and particles in ‘ 94 CS 480/680 Chapter 12 -- Visualization 62

n Many other visualization strategies are discussed in Glassner’s book n One approach to building visualization applications is to use an object oriented toolkit. This was presented in The Visualization Toolkit by Schroeder, et. al. n The IEEE Transactions on Visualization and Computer Graphics contain many examples of recent work in Scientific Visualization. CS 480/680 Chapter 12 -- Visualization 63

Exercises -- Due next class CS 480/680 Chapter 12 -- Visualization 64