Vectors in Two and Three Dimensions Copyright Cengage

Vectors in Two and Three Dimensions Copyright © Cengage Learning. All rights reserved.

9. 4 Vectors in Three Dimensions Copyright © Cengage Learning. All rights reserved.

Objectives ► Vectors in Space ► Combining Vectors in Space ► The Dot Product for Vectors in Space 3

Vectors in Three Dimensions Vectors in space have a direction that is in three-dimensional space. The properties that hold for vectors in the plane hold for vectors in space as well. 4

Vectors in Space 5

Vectors in Space When we place a vector a in space with its initial point at the origin, we can describe it algebraically as an ordered triple: a = a 1, a 2, a 3 where a 1, a 2 and a 3 are the components of a (see Figure 1). a = a 1, a 2, a 3 Figure 1 6

Vectors in Space A vector has many different representations, depending on its initial point. The following definition gives the relationship between the algebraic and geometric representations of a vector. 7

Example 1 – Describing Vectors in Component Form (a) Find the components of the vector a with initial point P(1, – 4, 5) and terminal point Q(3, 1, – 1). (b) If the vector b = – 2, 1, 3 has initial point (2, 1, – 1), what is its terminal point? 8

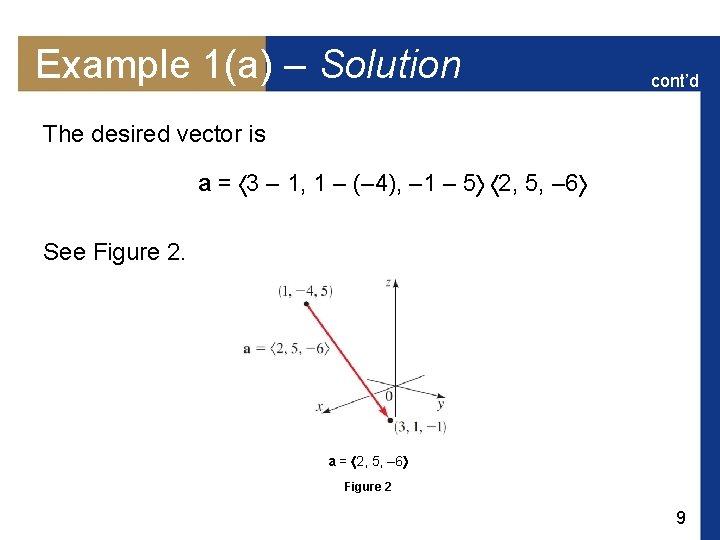
Example 1(a) – Solution cont’d The desired vector is a = 3 – 1, 1 – (– 4), – 1 – 5 2, 5, – 6 See Figure 2. a = 2, 5, – 6 Figure 2 9

Example 1(b) – Solution cont’d Let the terminal point of b be (x, y, z). Then b = x – 2, y – 1, z – (– 1) Since b = – 2, 1, 3 we have x – 2 = – 2, y – 1 = 1, and z + 1 = 3. So x = 0, y = 2, and z = 2, and the terminal point is (0, 2, 2). 10

Vectors in Space The following formula is a consequence of the Distance Formula, since the vector in a = a 1, a 2, a 3 standard position has initial point (0, 0, 0) and terminal point (a 1, a 2, a 3). 11

Example 2 – Magnitude of Vectors in Three Dimensions Find the magnitude of the given vector. (a) u = 3, 2, 5 (b) v = 0, 3, – 1 (c) w = 0, 0, – 1 Solution: (a) (b) (c) 12

Combining Vectors in Space 13

Combining Vectors in Space We now give definitions of the algebraic operations involving vectors in three dimensions. 14

Example 3 – Operations with Three-Dimensional Vectors Find the magnitude of the given vector. If u = 1, – 2, 4 and v = 6, – 1, 1 find u + v, u – v, and 5 u – 3 v. Solution: Using the definitions of algebraic operations we have u + v = 1 + 6, – 2 – 1, 4 + 1 = 7, – 3, 5 15

Combining Vectors in Space A unit vector is a vector of length 1. The vector w in Example 2(c) is an example of a unit vector. Some other unit vectors in three dimensions are i = 1, 0, 0 j = 0, 1, 0 k = 0, 0, 1 as shown in Figure 3 17

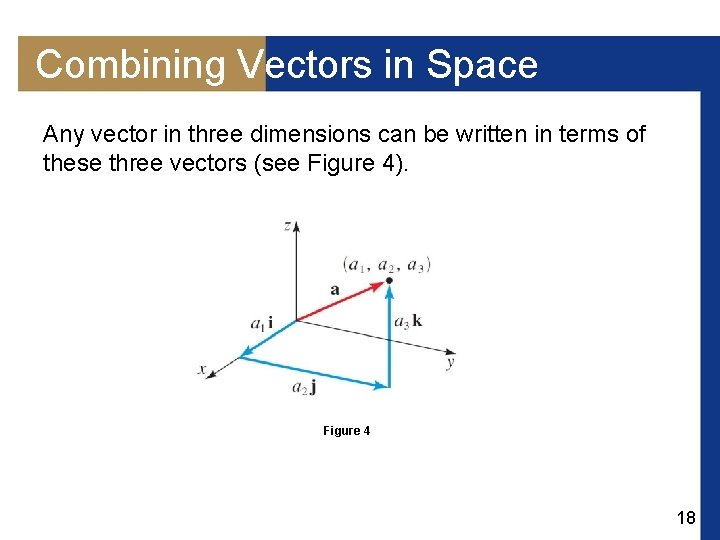
Combining Vectors in Space Any vector in three dimensions can be written in terms of these three vectors (see Figure 4). Figure 4 18

Combining Vectors in Space All the properties of vectors hold for vectors in three dimensions as well. We use these properties in the next example. 19

Example 4 – Vectors in Terms of i, j, and k (a) Write the vector u = 5, – 3, 6 in terms of i, j, and k. (b) If u = i + 2 j – 3 k and v = 4 i + 7 k, express the vector 2 u + 3 v in terms of i, j, and k. Solution: (a) u = 5 i + (– 3)j + 6 k = 5 i – 3 j + 6 k 20

Example 4 – Solution cont’d (b) We use the properties of vectors to get the following: 2 u + 3 v = 2(2 i + 2 j – 3 k) + 3(4 i + 7 k) = 4 i + 4 j – 6 k + 12 i + 21 k = 16 i + 4 j + 15 k 21

The Dot Product for Vectors in Space 22

The Dot Product for Vectors in Space We define the dot product for vectors in three dimensions. All the properties of the dot product, including the Dot Product Theorem, hold for vectors in three dimensions. 23

Example 5 – Calculating Dot Products for Vectors in Three Dimensions Find the given dot product. (a) – 1, 2, 3 6, 5, – 1 (b) (2 i – 3 j – k) (–i + 2 j + 8 k) Solution: (a) – 1, 2, 3 6, 5, – 1 = (– 1)(6) + (2)(5) + (3)(– 1) =1 (b) (2 i – 3 j – k) (–i + 2 j + 8 k) = 2, – 3, – 1, 2, 8 = (2)(– 1) + (– 3)(2) + (– 1)(8) = – 16 24

The Dot Product for Vectors in Space The cosine of the angle between two vectors can be calculated using the dot product. The same property holds for vectors in three dimensions. 25

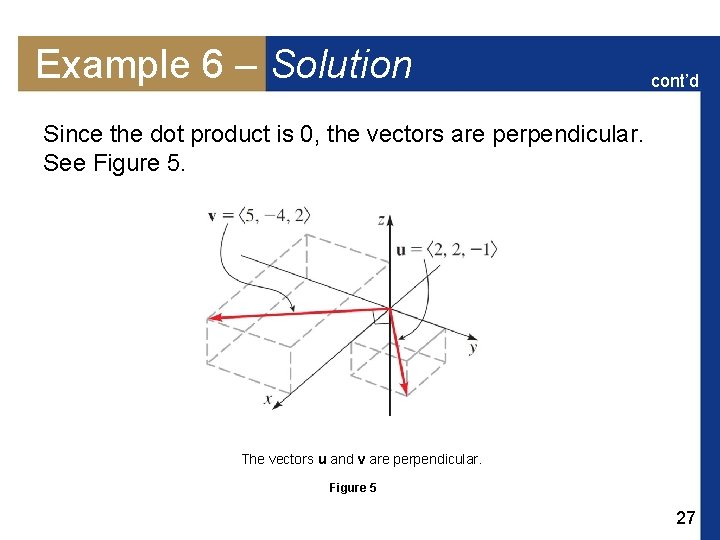
Example 6 – Checking Vectors for Perpendicularity Show that the vector u = 2 i + 2 j – k is perpendicular to 5 i – 4 j + 2 k. Solution: We find the dot product. (2 i + 2 j – k) (5 i – 4 j + 2 k) = (2)(5) + (2)(– 4) + (– 1)(2) =0 26

Example 6 – Solution cont’d Since the dot product is 0, the vectors are perpendicular. See Figure 5. The vectors u and v are perpendicular. Figure 5 27

Direction Angles of a Vector 28

Direction Angles of a Vector The direction angles of a nonzero vector a = a 1 i + a 2 j + a 3 k are the angles , β, and γ in the interval [0, ] that the vector a makes with the positive x-, y-, and zaxes (see Figure 6). Direction angles of the vector a Figure 6 29

Direction Angles of a Vector The cosines of these angles, cos β, and cos γ, are called the direction cosines of the vector a. By using the formula for the angle between two vectors, we can find the direction cosines of a: 30

Direction Angles of a Vector 31

Example 7 – Finding the Direction Angles of a Vector Find the direction angles of the vector a = i + 2 j + 3 k. Solution: The length of the vector a is | a | = From the direction angles formula we get = . 32

Example 7 – Solution cont’d Since the direction angles are in the interval [0, ] and since cos– 1 gives angles in that same interval, we get , β, and γ by simply taking cos– 1 of the above equations. 33

Direction Angles of a Vector The direction angles of a vector uniquely determine its direction, but not its length. If we also know the length of the vector a, the expressions for the direction cosines of a allow us to express the vector as From this we get a = | a | cos , cos β, cos γ = cos , cos β, cos γ 34

Direction Angles of a Vector Since a/| a | is a unit vector we get the following. This property indicates that if we know two of the direction cosines of a vector, we can find the third up to its sign. 35

Example 8 – Finding the Direction Angles of a Vector A vector makes an angle = /3 with the positive x-axis and an angle β = 3 /4 with the positive y-axis. Find the angle γ that the vector makes with the positive z-axis, given that γ is an obtuse angle. Solution: By the property of the direction angles we have 36

Example 8 – Solution cont’d Since we require γ to be an obtuse angle, we conclude that γ = 2 /3. 37