Using Nuclear Spins for Quantum Information Processing and

Using Nuclear Spins for Quantum Information Processing and Quantum Computing David G. Cory Department of Nuclear Engineering Massachusetts Institute of Technology

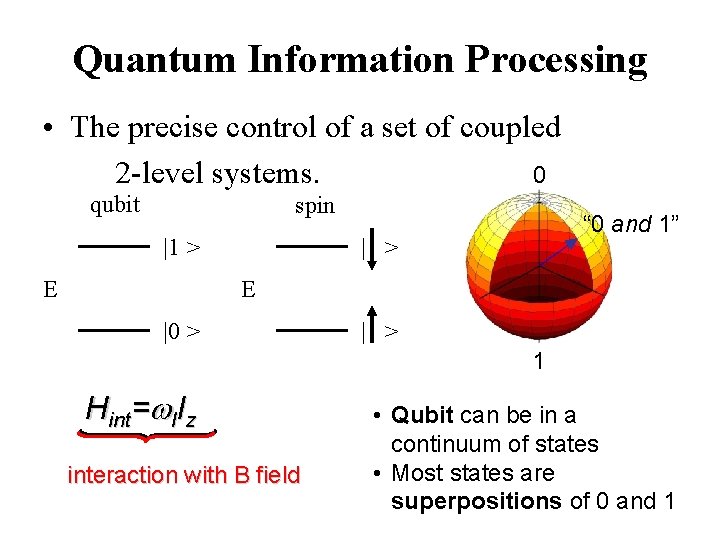
Quantum Information Processing • The precise control of a set of coupled 2 -level systems. 0 qubit spin |1 > E “ 0 and 1” | > E |0 > | > 1 Hint=w. IIz interaction with B field • Qubit can be in a continuum of states • Most states are superpositions of 0 and 1

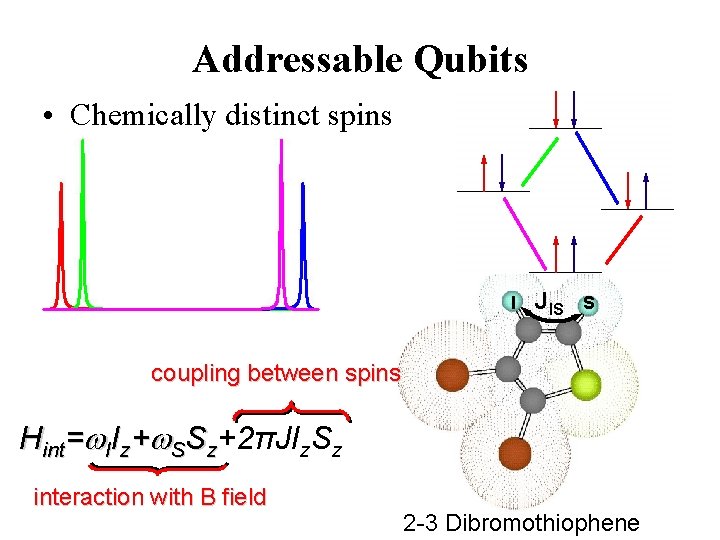
Addressable Qubits • Chemically distinct spins I JIS S coupling between spins Hint=w. IIz+w. SSz+2πJIz. Sz interaction with B field 2 -3 Dibromothiophene

External Hamiltonian – Experimentally Controlled Hamiltonian: Hext(t) =w. RFx(t)·(Ix+Sx)+w. RFy(t)·(Iy+Sy) spins couple to RF field – Total Hamiltonian: I JIS S 9. 6 T Htotal (t) = Hint + Hext(t) Htotal(t) controlled via Hext(t) RF wave

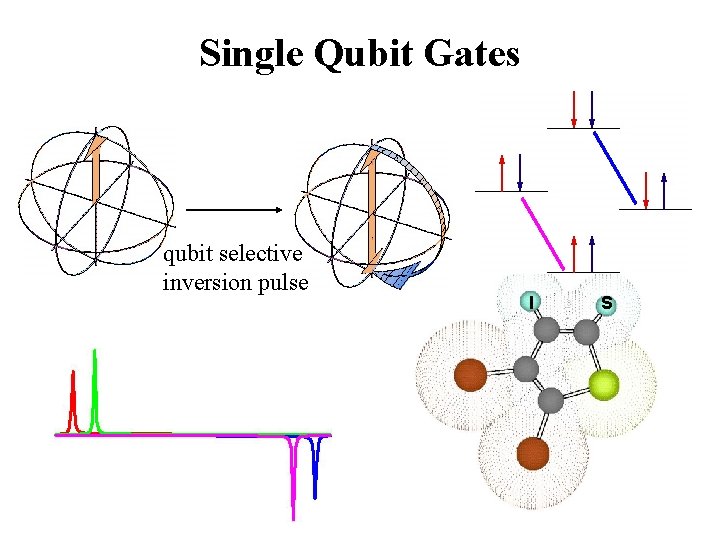
Single Qubit Gates qubit selective inversion pulse I S

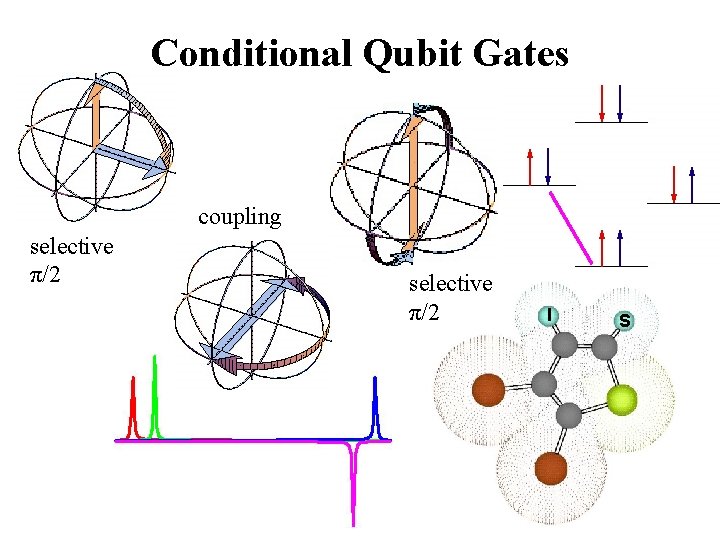
Conditional Qubit Gates coupling selective π/2 I S

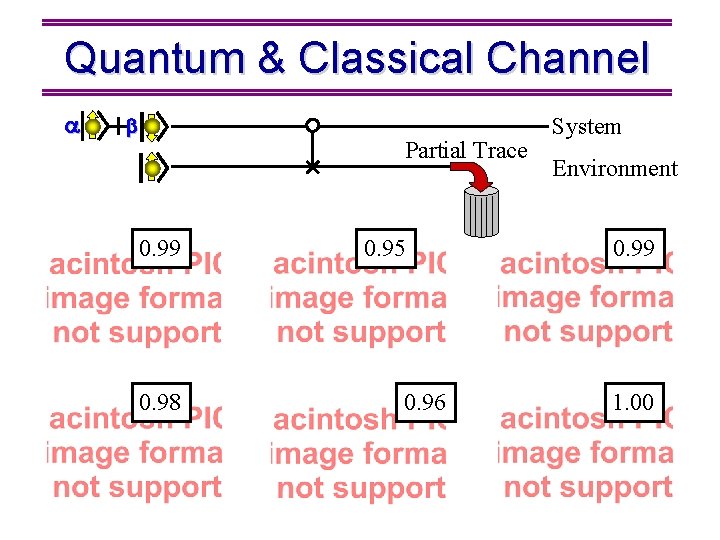
Quantum & Classical Channel Partial Trace 0. 99 0. 98 0. 95 0. 96 System Environment 0. 99 1. 00

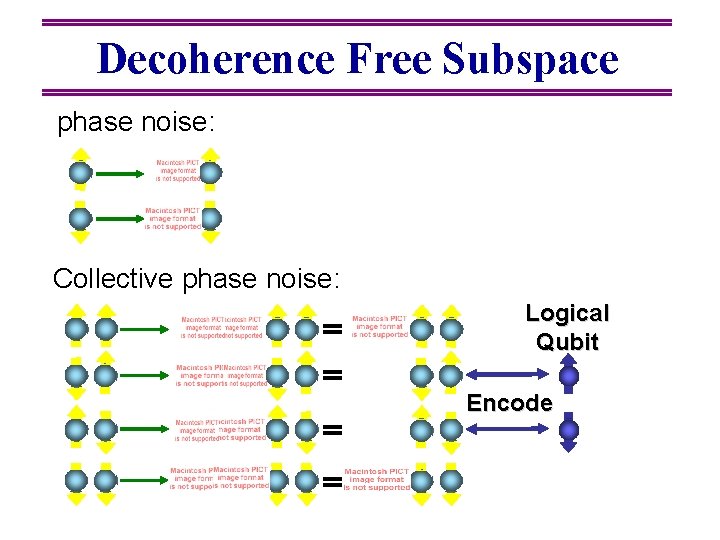
Decoherence Free Subspace phase noise: Collective phase noise: Logical Qubit Encode

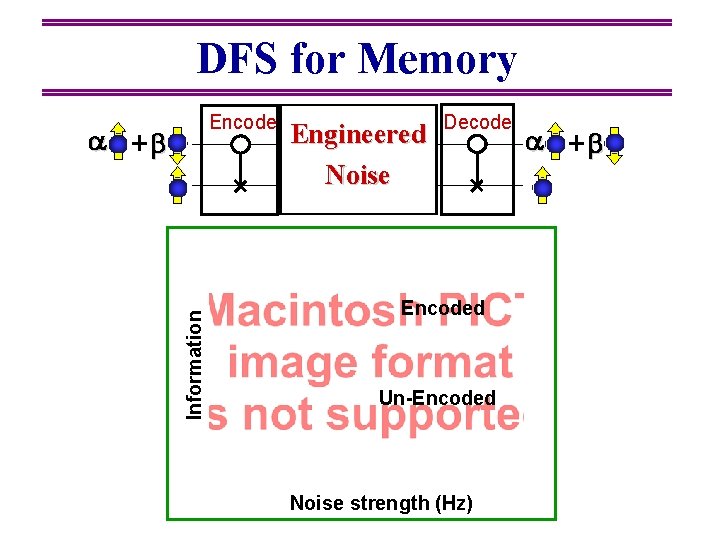
DFS for Memory Information Encode Engineered Noise Decode Encoded Un-Encoded Noise strength (Hz)

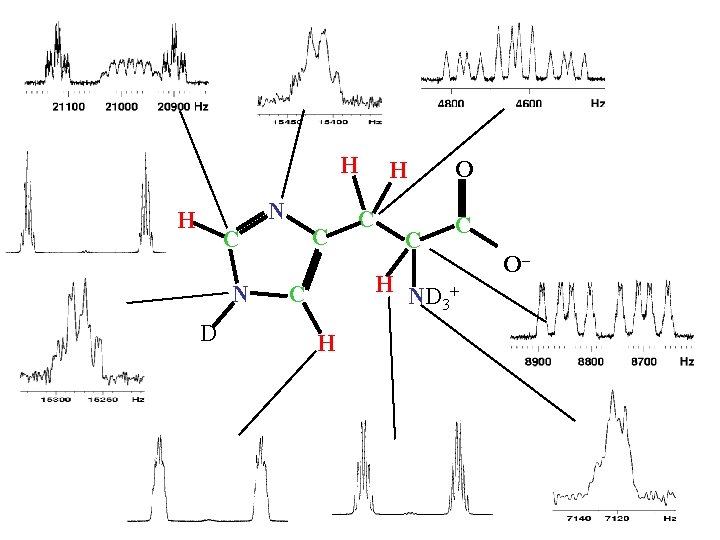
Samples and Hamiltonians Alanine (3 Qubits) Crotonic Acid (4 Qubits) J 13 J 12 C 1 J 12 C 3 J 23 C 2 C 1 J 23 J 34 C 3

H N H C C N D H C C O C H ND + 3 C H O–

Control of Entanglement GHZ State C=0. 88 Z Measurement C=0. 89 W State C=0. 73 X Measurement C=0. 92 Traced state C=0. 71 Z Measurement C=0. 80 X Measurement C=0. 77 Traced state

Entangle bits 1 & 2, and bits 3 & 4 |01> + |10> Map bits 2 & 3 onto the Bell basis H Measurement of bits 2 & 3 Strong Measurement |01> + |10> Pseudopure state - Product of two Singlet states (real part of the density matrix)

Final Results – After Selective Strong Measurement in the Bell basis

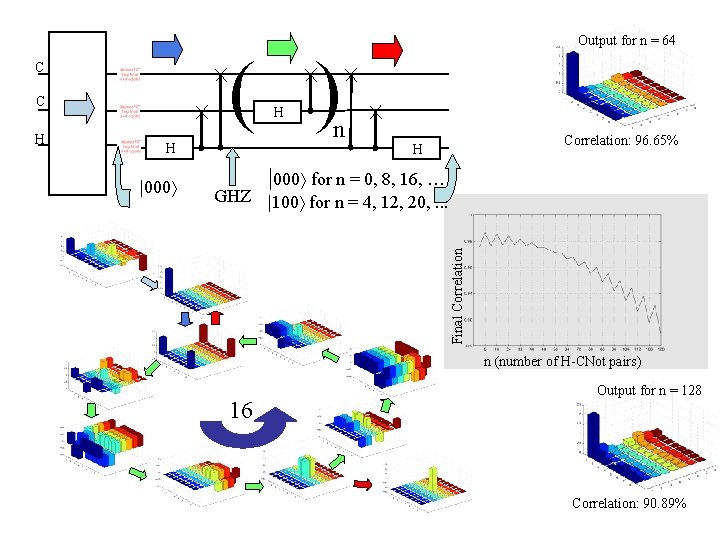
( ) C C H H |000 n Correlation: 96. 65% H |000 for n = 0, 8, 16, … GHZ |100 for n = 4, 12, 20, . . . Final Correlation H Output for n = 64 n (number of H-CNot pairs) 16 Output for n = 128 Correlation: 90. 89%

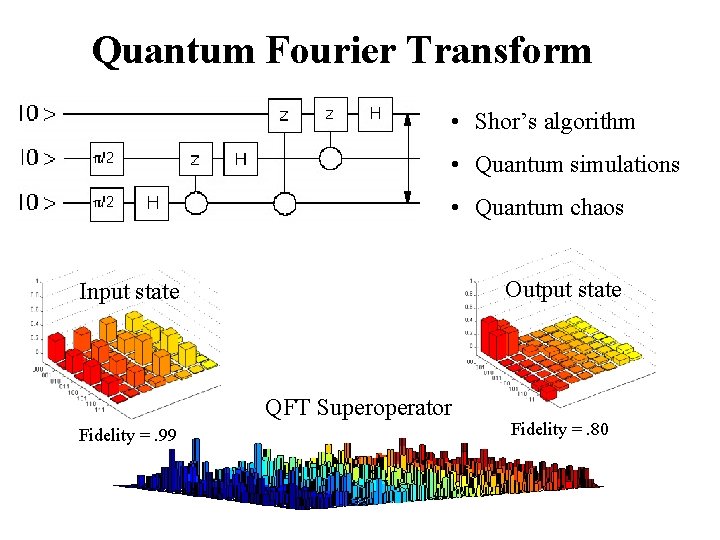
Quantum Fourier Transform • Shor’s algorithm • Quantum simulations • Quantum chaos Output state Input state QFT Superoperator Fidelity =. 99 Fidelity =. 80

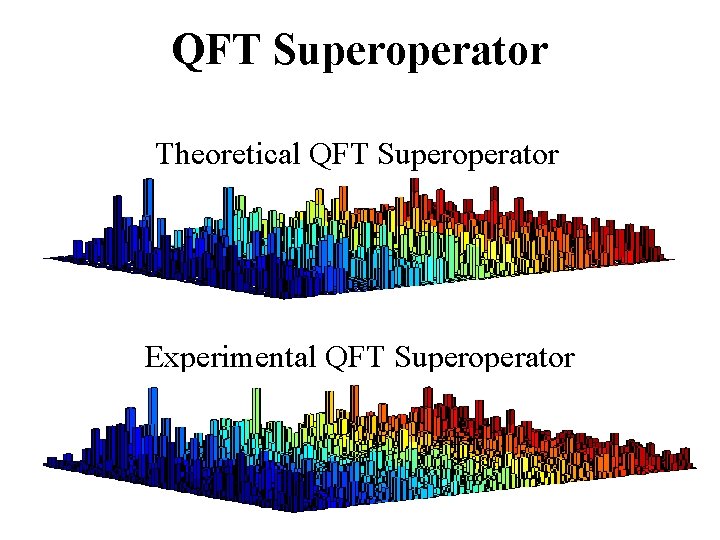
QFT Superoperator Theoretical QFT Superoperator Experimental QFT Superoperator

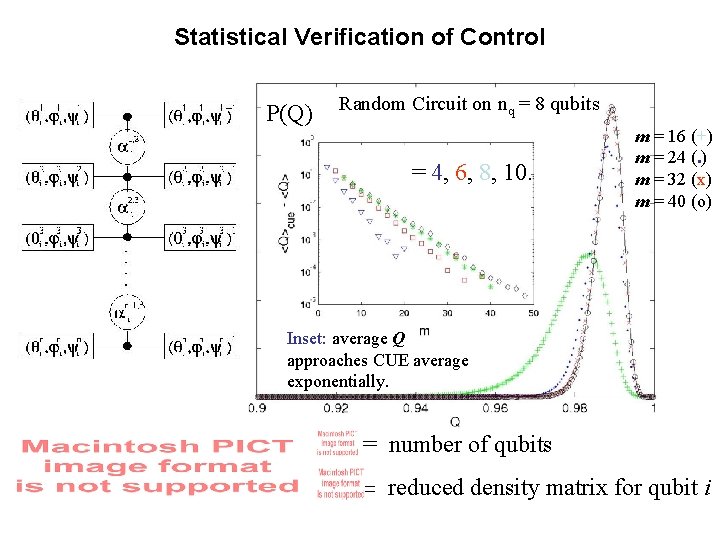
Statistical Verification of Control P(Q) Random Circuit on nq = 8 qubits = 4, 6, 8, 10. m = 16 (+) m = 24 (. ) m = 32 (x) m = 40 (o) Inset: average Q approaches CUE average exponentially. = number of qubits = reduced density matrix for qubit i

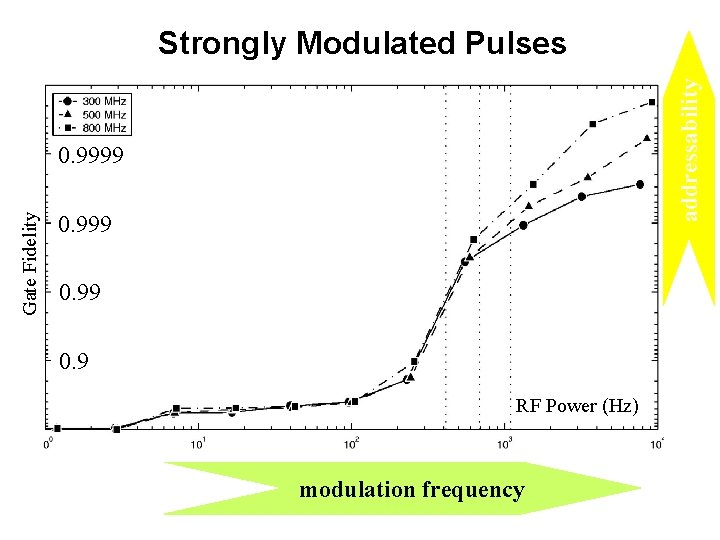
addressability Strongly Modulated Pulses Gate Fidelity 0. 9999 0. 9 RF Power (Hz) modulation frequency

Why is quantum noise so bad? Consider an entangled state: If any are disturbed, they all collapse To make matters worse: • Can’t Copy No Majority Coding • Can’t Look How do we protect our information?

Quantum Error Correction If the noise is sufficiently weak compared with your control rates then you correct a subset of errors with only a finite accuracy requirements. Encoder Memory Extra Bits Regularly Correct Error Decoder Discarded Bits

Arbitrary Collective Noise Expand your state space in the joint eigenstates of J 2 and Jz (0)12 (1/2)3 (1/2)123 (1/2)1 (1/2)2 (1)12 (1/2)3 J can’t distinguish between the 2 paths to the (1/2) state. (3/2)123

Experimental Results Information Weak Noise No Encoding, Y Noise Encoded, Y, Z Noise Strength (Hz) Strong Noise Limit Info Un-Encoded Z-X Noise NS-Encoded No Noise Z-X Noise Z-Y Noise 0. 24 0. 70

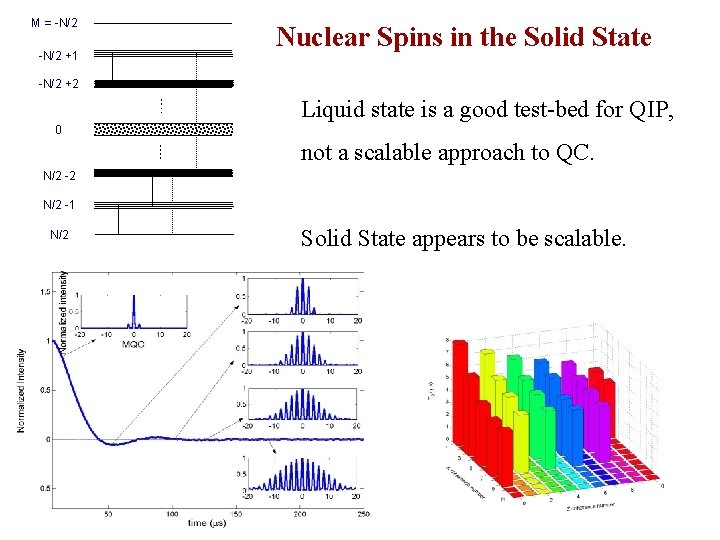
M = -N/2 +1 Nuclear Spins in the Solid State -N/2 +2 Liquid state is a good test-bed for QIP, 0 not a scalable approach to QC. N/2 -2 N/2 -1 N/2 Solid State appears to be scalable.

Spin Hamiltonian Htot = HZ + HD Zeeman Hamiltonian + Secular Dipolar Hamiltonian w = g. B 0 (w >> w. Dij) • use chemistry locally for error correction • use spatial addressing to define qubits (magnetic field gradients) • dipolar to nearest neighbor coupling + • single spin detection +

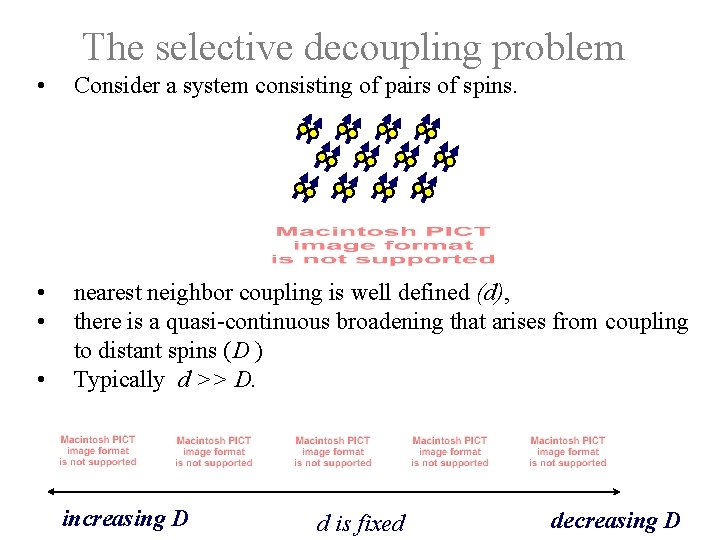
The selective decoupling problem • Consider a system consisting of pairs of spins. • • nearest neighbor coupling is well defined (d), there is a quasi-continuous broadening that arises from coupling to distant spins (D ) Typically d >> D. • increasing D d is fixed decreasing D

Dipolar -> nn

Status of NMR QIP The zero-order average Hamiltonian is, where J 0(x) and H 0(x) are the zeroth order Bessel and Struve functions

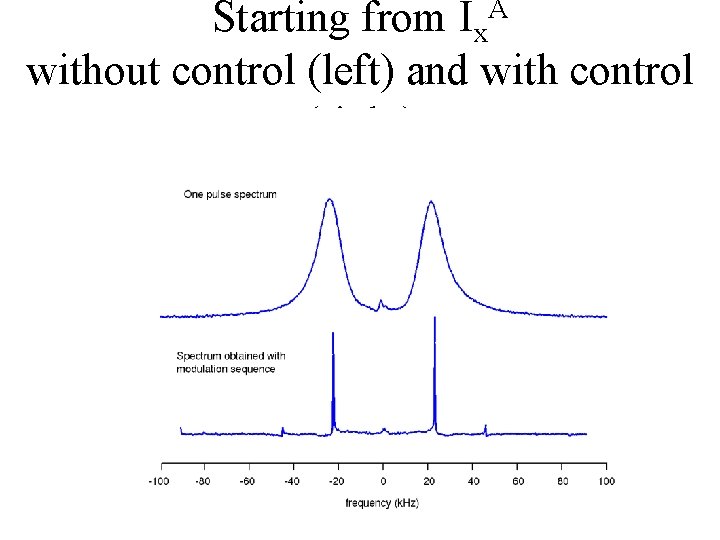
Starting from Ix. A without control (left) and with control (right) BLUE: Ix. A; BROWN: Ix. B; BLACK: Ix. C BC coupling = 1/8 AB coupling

Starting from Ix. A without control (left) and with control (right)

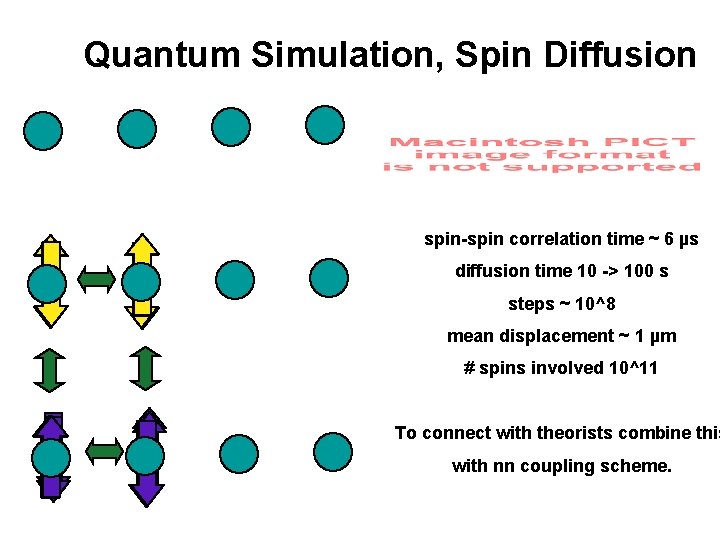
Quantum Simulation, Spin Diffusion spin-spin correlation time ~ 6 µs diffusion time 10 -> 100 s steps ~ 10^8 mean displacement ~ 1 µm # spins involved 10^11 To connect with theorists combine this with nn coupling scheme.

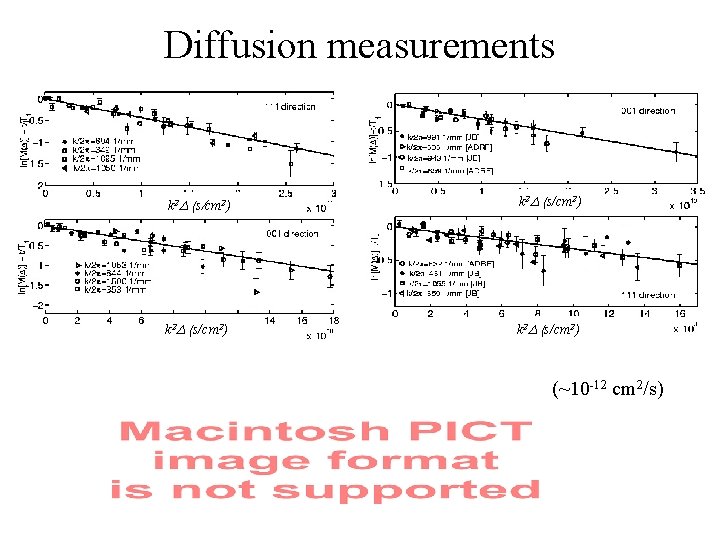
Diffusion measurements k 2 D (s/cm 2) (~10 -12 cm 2/s)

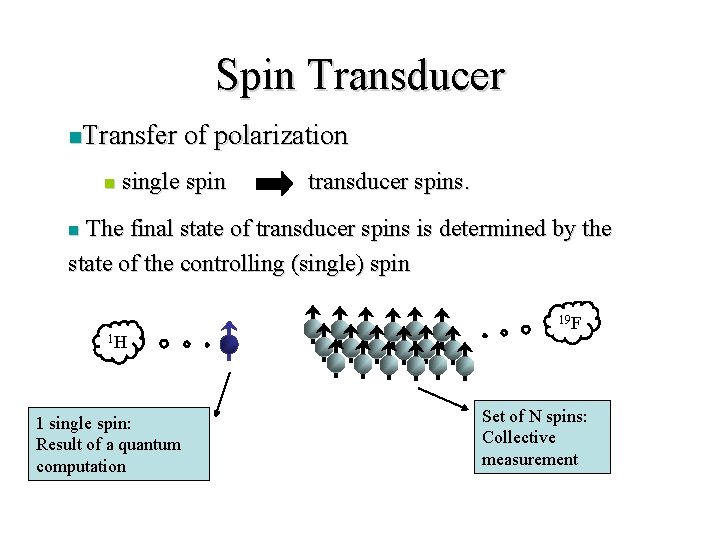
Spin Transducer n. Transfer n of polarization single spin transducer spins. The final state of transducer spins is determined by the state of the controlling (single) spin n 1 H 1 single spin: Result of a quantum computation 19 F Set of N spins: Collective measurement

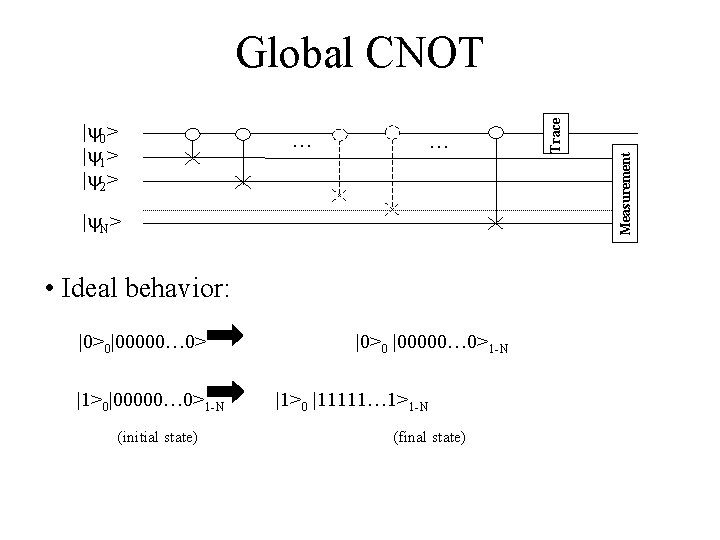
… … |y. N> • Ideal behavior: |0>0|00000… 0> |1>0|00000… 0>1 -N (initial state) |0>0 |00000… 0>1 -N |1>0 |11111… 1>1 -N (final state) Measurement |y 0> |y 1> |y 2> Trace Global CNOT

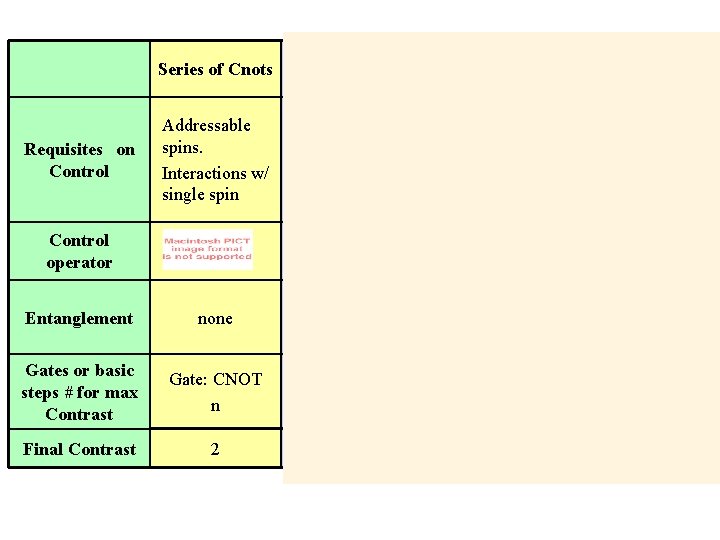
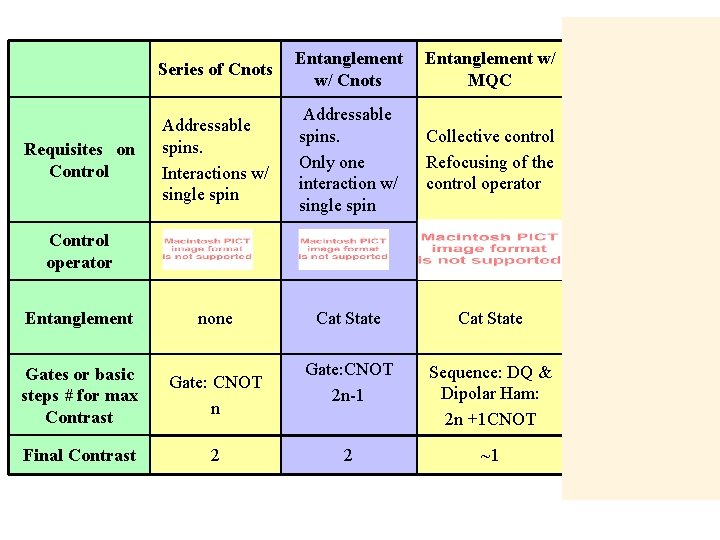
Series of Cnots Requisites on Control Addressable spins. Interactions w/ single spin Control operator Entanglement none Gates or basic steps # for max Contrast Gate: CNOT n Final Contrast 2

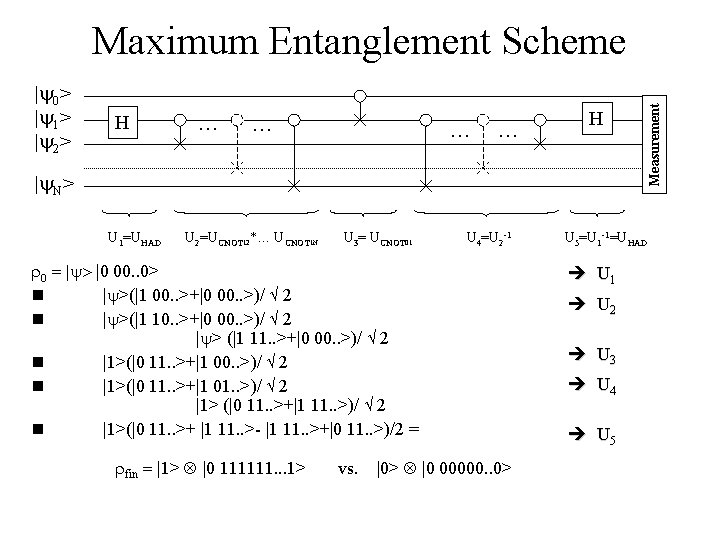
|y 0> |y 1> |y 2> H … … H |y. N> U 1=UHAD U 2=UCNOT 12*… UCNOT 1 N U 3= UCNOT 01 U 4=U 2 -1 r 0 = |y> |0 00. . 0> n |y>(|1 00. . >+|0 00. . >)/ 2 n |y>(|1 10. . >+|0 00. . >)/ 2 |y> (|1 11. . >+|0 00. . >)/ 2 n |1>(|0 11. . >+|1 01. . >)/ 2 |1> (|0 11. . >+|1 11. . >)/ 2 n |1>(|0 11. . >+ |1 11. . >- |1 11. . >+|0 11. . >)/2 = rfin = |1> |0 111111. . . 1> vs. |0> |0 00000. . 0> Measurement Maximum Entanglement Scheme U 5=U 1 -1=UHAD è U 1 è U 2 è U 3 è U 4 è U 5

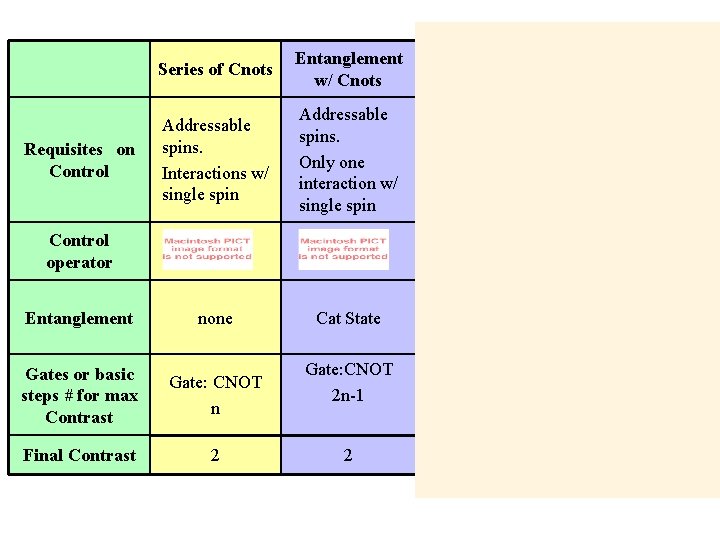
Requisites on Control Series of Cnots Entanglement w/ MQC Addressable spins. Interactions w/ single spin Addressable spins. Only one interaction w/ single spin • Collective control • Refocusing of the control operator Perturbative approach • Collective control Control operator Entanglement none Gates or basic steps # for max Contrast Gate: CNOT n Final Contrast 2 Cat State Ground State of Heisenberg Hamiltonian Gate: CNOT 2 n-1 Sequence: DQ & Dipolar Ham: 2 n +1 CNOT Sequence: DQ 1 & Dipolar Hamiltonian: ~n 2 ~1 ~1

Creation of Cat State With the N-quantum Grade Raising operator: the pure state is transformed into the cat state:

Requisites on Control Series of Cnots Entanglement w/ MQC Perturbative approach Addressable spins. Interactions w/ single spin Addressable spins. Only one interaction w/ single spin Collective control Refocusing of the control operator • Collective control Control operator Entanglement none Gates or basic steps # for max Contrast Gate: CNOT n Final Contrast 2 Cat State Ground State of Heisenberg Hamiltonian Gate: CNOT 2 n-1 Sequence: DQ & Dipolar Ham: 2 n +1 CNOT Sequence: DQ 1 & Dipolar Hamiltonian: ~n 2 ~1 ~1

Quantum Transducer • Model: – linear chain of spins. – all the couplings are taken into account. • Limited number of spins. • Simulated all the pulse sequences needed for the wanted propagators, • varying the # of repetitions of the cycle.

Results: Entanglement Scheme • Simulations (8 spins) 1 Global Entanglement of 1 st spin

Conclusions • • Liquid state NMR is a useful QIP test-bed ~ 8 qubits. Systems of dipole coupled spins are universal for QIP. Solid state, nuclear spin approaches appear to be scalable. For selected problems we are already beyond the capabilities of classical computing. • Introduced a quantum transducer that uses entanglement to make a classical measurement that could not otherwise be realized.

Dr. Timothy Havel Professor Seth Lloyd Professor Raymond Laflamme Dr. Chandrasekhar Ramanathan Dr. Joseph Emerson Dr. Grum Teklemariam Dr. Marco Pravia Dr. Evan Fortunato Dr. Greg Boutis Dr. Yaakov Weinstein Nicolas Boulant Paola Cappellaro Zhiying (Debra) Chen Hyung Joon Cho Daniel Greenbaum Jonathan Hodges Suddhasattwa Sinha