urm simulator online https sites oxy edurnaimihom eURMsim

urm simulator online https: //sites. oxy. edu/rnaimi/hom e/URMsim. htm

URM = UNLIMITED REGISTER MACHINE Idealizzazione matematica di di un calcolatore ideata nel 1963 da J. C. Shepherdson e H. E. Sturgis. Funzioni URM – computabili

Una URM ha un numero potenzialmente infinito di registri. R 0 R 1 R 2 R 3 R 4 … … Ogni registro Ri contiene un numero naturale ri Il contenuto dei registri può essere modificato dalla URM sulla base dell’esecuzione di istruzioni che la URM è in grado di riconoscere. Una sequenza finita di istruzioni, I 1, I 2, … , In è detta Programma Funzioni URM – computabili

Computazione su una URM n n Configurazione iniziale Programma P: I 1, I 2, ……, Im La URM esegue la computazione eseguendo in sequenza le istruzioni I 1, I 2, . . . In e sulla base delle istruzioni che legge, il contenuto dei registri può essere o meno modificato. L’esecuzione del programma termina quando le istruzioni terminano. Funzioni URM – computabili

ISTRUZIONI • Z(n) rn: = 0 Esempio: Supponiamo che la URM sia nella seguente configurazione: R 0 R 1 10 3 R 2 R 3 R 4 … 4 0 6 … l’istruzione Z(2) trasforma la configurazione in R 0 R 1 R 2 R 3 R 4 … 10 3 Funzioni URM – computabili 0 0 6 …

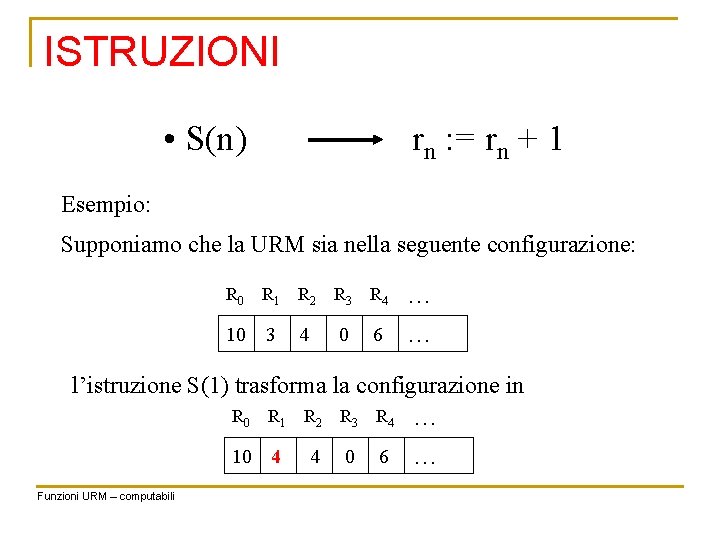
ISTRUZIONI • S(n) rn : = rn + 1 Esempio: Supponiamo che la URM sia nella seguente configurazione: R 0 R 1 10 3 R 2 R 3 R 4 … 4 0 6 … l’istruzione S(1) trasforma la configurazione in R 0 R 1 R 2 R 3 R 4 … 10 4 Funzioni URM – computabili 4 0 6 …

ISTRUZIONI • T(m, n) rn : = rm Esempio: Supponiamo che la URM sia nella seguente configurazione: R 0 R 1 10 3 R 2 R 3 R 4 … 4 0 6 … l’istruzione T(3, 0) trasforma la configurazione in R 0 R 1 R 2 R 3 R 4 … 0 Funzioni URM – computabili 3 4 0 6 …

ISTRUZIONI • J(m, n, q) Se rm ≠ rn esegue l'istruzione successiva nel programma Se rm = rn salta all'istruzione q nel programma. Esempio: Supponiamo che la configurazione iniziale sia R 0 R 1 R 2 0 3 1 E che il programma contenga le seguenti istruzioni: 1. … 0 … R 3 S(2) 2. J(1, 2, 4) 3. J(1, 1, 1) 4. T(2, 0) Cosa avviene durante la computazione del Programma P? Funzioni URM – computabili

R 0 R 1 R 2 0 3 2 … 0 3 2 0 … Istruzione 2 – r 1 ≠ r 2 prosegue con l’istruzione successiva 0 3 2 0 … Istruzione 3 – r 1 = r 1 salta all’istruzione 1 0 3 3 0 … Istruzione 1 – S(2) R 3 Istruzione 1 – S(2) 0 3 3 0 … Istruzione 2 – r 1 = r 2 salta all’istruzione 4 3 3 3 0 … Istruzione 4 – T(2, 0) Funzioni URM – computabili

Funzioni URM - computabili Sia f: Nn N Diremo che f è URM- computabile se dato un input (a 0, a 1, …an) esiste un programma P tale che P sulla configurazione iniziale (a 0, a 1, …an, 0, 0, … 0) termina. Per convenzione l’output della computazione sarà posto in R 0 Funzioni URM – computabili

Un esempio La funzione f(x, y)=x+y è computabile? L’idea alla base del programma è la seguente: sommo 1 a x, usando la funzione S(x), y volte. Configurazione Iniziale: Programma R 0 R 1 0 x R 2 y R 3 0 1. T(1, 0) 2. J(3, 2, 6) 3. S(0) 4. S(3) 5. J(1, 1, 2) La configurazione finale sarà Funzioni URM – computabili x+y x y y

“ 3+2”=? R 0 R 1 R 2 R 3 0 3 2 3 3 2 … 0 … 3 3 2 0 4 3 2 … 0 … 1 … 4 3 2 1 5 3 2 … 1 … 5 3 2 2 … Istruzione 4 – S(3) 5 3 2 2 … Istruzione 5 – r 1 = r 1 salta all’istruzione 2 Istruzione 2 – r 2 = r 3 l’istruzione 6 non esiste la computazione termina. r 0 = 5 … Configurazione iniziale Istruzione 1 – T(1, 0) Istruzione 2 – r 2 ≠ r 3 prosegue con l’istruzione successiva Istruzione 3 – S(0) Istruzione 4 – S(3) Istruzione 5 – r 1 = r 1 salta all’istruzione 2 Istruzione 2 – r 2 ≠ r 3 prosegue con l’istruzione successiva Istruzione 3 – S(0) 3+2=5!

La funzione f = x+y è quindi URM-computabile Funzioni URM – computabili

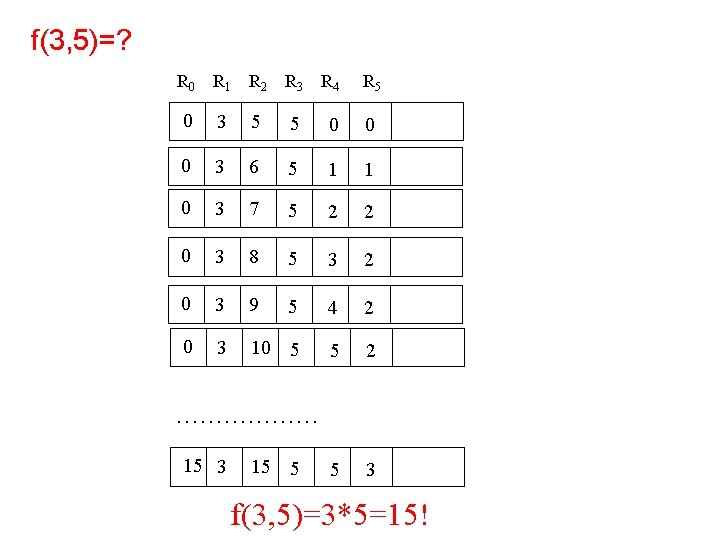
Un esempio La funzione f(x, y)=x*y è computabile? 1. T(2, 3) 2. Z(5) 3. S(5) 4. J(5, 1, 10) 5. Z(4) 6. S(2) 7. S(4) 8. J(4, 3, 3) 9. J(1, 1, 6) 10. T(2, 0) Funzioni URM – computabili

f(3, 5)=? R 0 R 1 R 2 R 3 R 4 R 5 0 3 5 5 0 0 0 3 6 5 1 1 0 3 7 5 2 2 0 3 8 5 3 2 0 3 9 5 4 2 0 3 10 5 5 2 5 3 ……………… 15 3 15 5 f(3, 5)=3*5=15!

Le URM fin qui trattate hanno considerato solo numeri naturali. Il concetto di computabilità illustrato si applica a funzioni sui numeri naturali. Lo stesso concetto può essere esteso anche ad altre strutture Sia D un Dominio, è possibile costruire una funzione g : D → N , detta codifica, tale che : per ogni d Є D g(d) Є N Sia f: D → D e f*: N→ N, la funzione che fa corrispondere a ogni d Є Dom(D) la codifica di f(d) in N, f*=g°f°g-1 Diremo che f è computabile se f* è computabile Funzioni URM – computabili

I numeri naturali sono quindi sufficienti per rappresentare ogni possibile struttura dati su cui si vogliono definire algoritmi. Funzioni URM – computabili

Lezione 2: Composizione di URM Funzioni URM – computabili

LINGUAGGI DI PROGRAMMAZIONE E URM Il modello di calcolo basato sulle URM, pur essendo un modello astratto, ha un diretto riferimento ai calcolatori e ai linguaggi di programmazione e consente di formalizzare i processi di esecuzione dei programmi Funzioni URM – computabili

Generazione di Funzioni Computabili A partire da funzioni URM-Computabili è possibile costruire altre funzioni URM-Computabili mediante schemi di: • Composizione • Ricorsione • Minimalizzazione Questa è ovviamente una proprietà molto potente dei programmi per le URM. Funzioni URM – computabili

Operazione di composizione generalizzata Siano date m funzioni gi : Nn→N, con i=1…m definite sul generico vettore x= (x 1, x 2, …, xn) a valori ai in N Sia f : Nm---N funzione sul vettore a=(a 1, a 2, …am) a valori in N Supponiamo che F, G 1, …. , Gm siano i programmi che calcolano rispettivamente f, g 1, …gm. PROBLEMA: Vogliamo simulare tramite le URM l’operazione di calcolo di f°gi = f(g 1, g 2, ……. . , gm) Dobbiamo considerare due aspetti: 1. Etichette del programma 2. Trattamento dei dati Funzioni URM – computabili

Etichette del programma Il primo problema è quello relativo alle etichette del programma; Ipotizziamo che i programmi F, G 1, …. , Gm siano espressi in forma standard. Un Programma è in forma standard se per tutte le istruzioni di jump J(m, n, s) si ha s <= l+1 dove l è la lunghezza del programma. Nel concatenare le Gi dobbiamo fare in modo che Gi cominci dove Gi-1 termina, per i=2, …, m. Funzioni URM – computabili

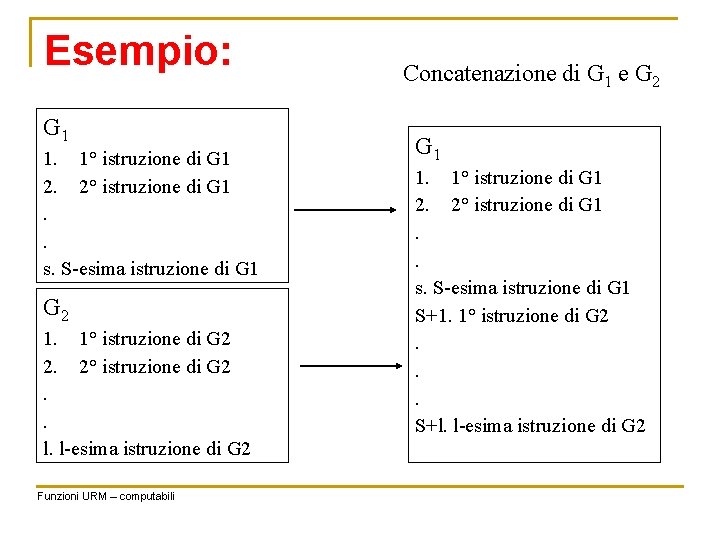
Esempio: G 1 1. 1° istruzione di G 1 2. 2° istruzione di G 1. . s. S-esima istruzione di G 1 G 2 1. 1° istruzione di G 2 2. 2° istruzione di G 2. . l. l-esima istruzione di G 2 Funzioni URM – computabili Concatenazione di G 1 e G 2 G 1 1. 1° istruzione di G 1 2. 2° istruzione di G 1. . s. S-esima istruzione di G 1 S+1. 1° istruzione di G 2. . . S+l. l-esima istruzione di G 2

…non solo! Le etichette presenti all’interno dei jump dovranno essere adeguate alle etichette del nuovo programma. Tornando al nostro esempio se in G 2 abbiamo un’istruzione di Jump del tipo J(m, n, k) bisognerà sommare s a k ottenendo J(m, n, k+s) Il secondo problema più complesso riguarda i dati; Come bisogna organizzare i registri della Urm in ordine alla operazione di composizione generalizzata dei Gi con F? Funzioni URM – computabili

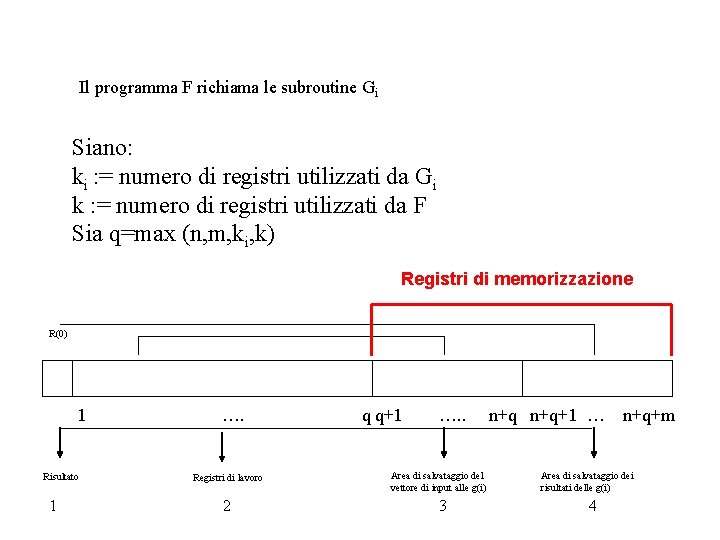
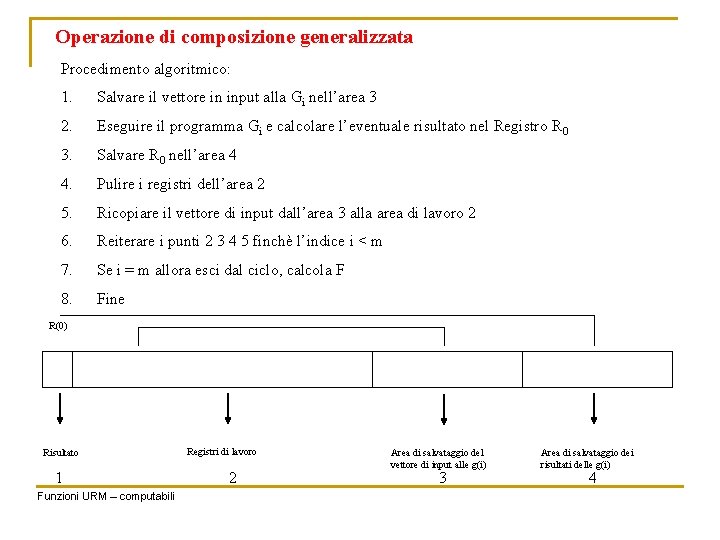
Il programma F richiama le subroutine Gi Siano: ki : = numero di registri utilizzati da Gi k : = numero di registri utilizzati da F Sia q=max (n, m, ki, k) Registri di memorizzazione R(0) 1 Risultato 1 …. Registri di lavoro 2 q q+1 …. . Area di salvataggio del vettore di input alle g(i) 3 n+q+1 … n+q+m Area di salvataggio dei risultati delle g(i) 4

Operazione di composizione generalizzata Procedimento algoritmico: 1. Salvare il vettore in input alla Gi nell’area 3 2. Eseguire il programma Gi e calcolare l’eventuale risultato nel Registro R 0 3. Salvare R 0 nell’area 4 4. Pulire i registri dell’area 2 5. Ricopiare il vettore di input dall’area 3 alla area di lavoro 2 6. Reiterare i punti 2 3 4 5 finchè l’indice i < m 7. Se i = m allora esci dal ciclo, calcola F 8. Fine R(0) Risultato 1 Funzioni URM – computabili Registri di lavoro 2 Area di salvataggio del vettore di input alle g(i) 3 Area di salvataggio dei risultati delle g(i) 4

ESEMPIO F(x, y)=m. c. m. (x, y) è computabile? Sia g 1(x, y)=x*y g 2(x, y)=M. C. D. (x, y) Se pongo F(g 1, g 2)=(g 1/g 2)= (x*y)/M. C. D. (x, y)=m. c. m. (x, y) Funzioni URM – computabili

Lezione 3: Ricorsione e minimalizzazione di URM Funzioni URM – computabili

Operazione di Ricorsione L’operazione di ricorsione può essere vista come una specializzazione della più generale operazione di composizione in cui la funzione coinvolta nell’operazione di composizione è sempre la stessa e la chiameremo pertanto funzione ricorsiva ed è applicata a sé stessa fino a raggiungere un livello limite chiamato livello 0 o livello assiomatico. Esempio: +(0, x)=x +(y+1, x)=S(+(y, x)) Funzioni URM – computabili

P* n n Dato un programma P(1, …, n) Definiamo il programma P*(l-1, …, l-n ->l) nel seguente modo Trasferisci i valori di l-1, …, l-n in 1, …, n calcola P trasferisci il risultato finale in l

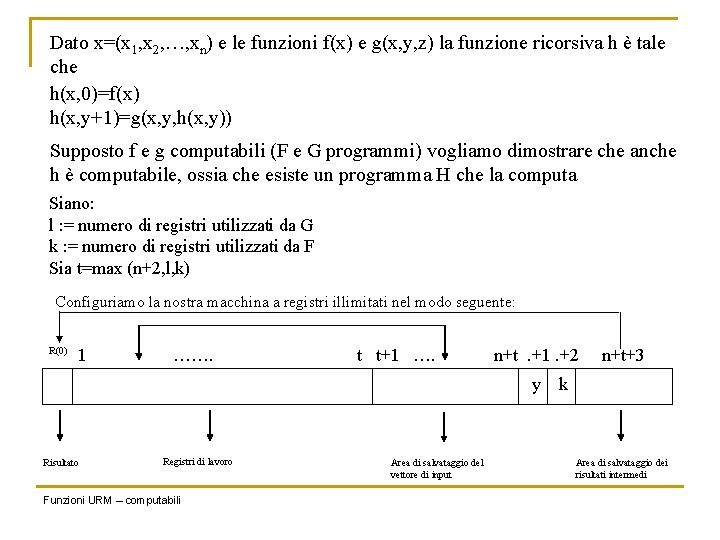
Dato x=(x 1, x 2, …, xn) e le funzioni f(x) e g(x, y, z) la funzione ricorsiva h è tale che h(x, 0)=f(x) h(x, y+1)=g(x, y, h(x, y)) Supposto f e g computabili (F e G programmi) vogliamo dimostrare che anche h è computabile, ossia che esiste un programma H che la computa Siano: l : = numero di registri utilizzati da G k : = numero di registri utilizzati da F Sia t=max (n+2, l, k) Configuriamo la nostra macchina a registri illimitati nel modo seguente: R(0) 1 ……. t t+1 …. n+t. +1. +2 y Risultato Registri di lavoro Funzioni URM – computabili Area di salvataggio del vettore di input n+t+3 k Area di salvataggio dei risultati intermedi

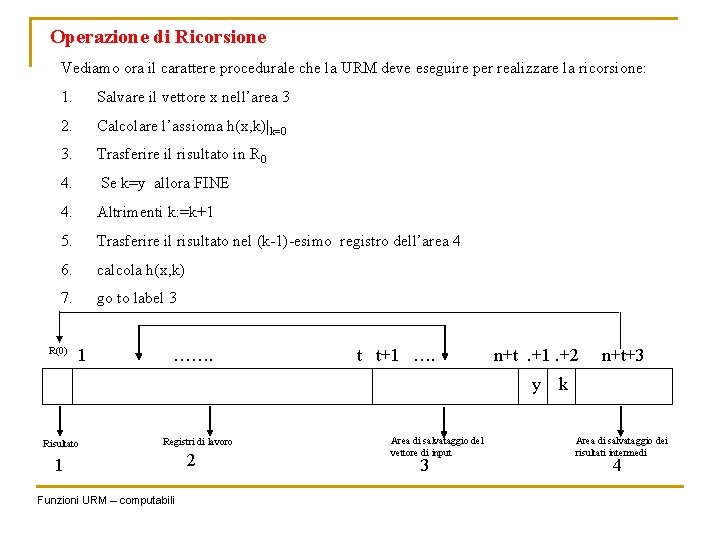
Operazione di Ricorsione Vediamo ora il carattere procedurale che la URM deve eseguire per realizzare la ricorsione: 1. Salvare il vettore x nell’area 3 2. Calcolare l’assioma h(x, k)|k=0 3. Trasferire il risultato in R 0 4. Se k=y allora FINE 4. Altrimenti k: =k+1 5. Trasferire il risultato nel (k-1)-esimo registro dell’area 4 6. calcola h(x, k) 7. go to label 3 R(0) 1 ……. t t+1 …. n+t. +1. +2 y Risultato Registri di lavoro 1 Funzioni URM – computabili 2 Area di salvataggio del vettore di input 3 n+t+3 k Area di salvataggio dei risultati intermedi 4

n n n n n T(1, m+1) … T(n+1, m+n+1) F*(1, 2, …, n ->t+3) q J(t+2, t+1, p) G*(m+1, …, m+n, t+2, t+3 ->t+3) S(t+2) J(1, 1, q) p T(t+3, 0)

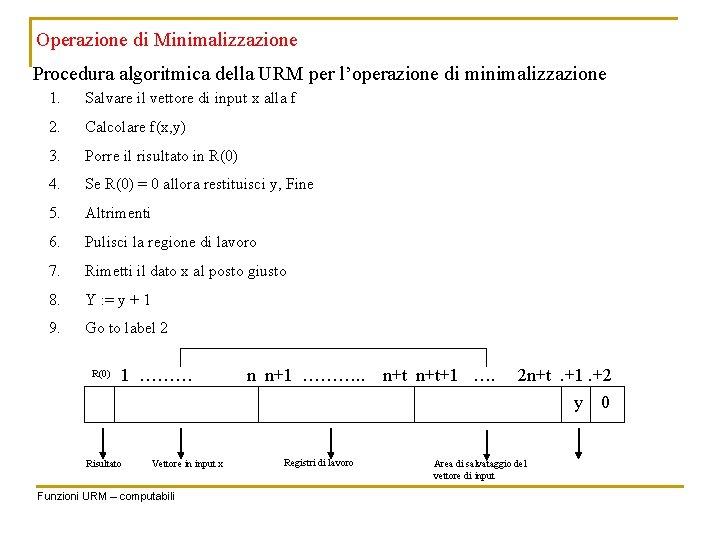
Operazione di Minimalizzazione Sia f(x, y) una funzione; nostro scopo è risolvere il problema di minimo Y = min yi (f(x, yi) = 0) Ovvero Y è il più piccolo intero naturale tra quelli che annullano la funzione f L’operazione di minimalizzazione può essere vista come una applicazione iterativa o anche ricorsiva della funzione f che ha termine quando tale funzione per un certo intero y e, in corrispondenza del vettore di input x, si annulla. t=numero di registri utilizzati da F. Configuriamo i registri della nostra urm che deve simulare l’operazione di minimalizzazione R(0) 1 ……… Risultato Vettore in input x Funzioni URM – computabili n n+1 ………. . Registri di lavoro n+t+1 …. 2 n+t. +1. +2 y 0 Area di salvataggio del vettore di input Contatore

Operazione di Minimalizzazione Procedura algoritmica della URM per l’operazione di minimalizzazione 1. Salvare il vettore di input x alla f 2. Calcolare f(x, y) 3. Porre il risultato in R(0) 4. Se R(0) = 0 allora restituisci y, Fine 5. Altrimenti 6. Pulisci la regione di lavoro 7. Rimetti il dato x al posto giusto 8. Y : = y + 1 9. Go to label 2 R(0) 1 ……… Risultato Vettore in input x Funzioni URM – computabili n n+1 ………. . Registri di lavoro n+t+1 …. 2 n+t. +1. +2 y 0 Area di salvataggio del vettore di input

n n n n T(1, m+1) … T(n, m+n) p F*(m+1, m+2, …m+n+1 ->1) J(1, m+n+2, q) S(m+n+1) J(1, 1, p) q T(m+n+1, 1)