Universit HassanII Facult des sciences An chock Khayarmarrakh

Université Hassan-II Faculté des sciences Aïn chock Khayar-marrakh q Cylindriques Réalisé par A. KHAYAR R. MARRAKH Professeurs assistants - département de physique

Les coordonnées cartésiennes employées habituellement pour représenter un point dans l'espace à trois dimensions ne sont pas toujours les plus appropriées. On retiendra deux autres types de coordonnées pour repérer un point ou décrire un champ ( scalaire ou vectoriel ) : les coordonnées cylindriques et les coordonnées sphériques.

Khayar-marrakh Pré requis : q Système de coordonnées cartésiennes q Grandeurs scalaires et vectorielles q Calcul vectoriel : produit scalaire, produit vectoriel, produit mixte… Objectifs : Au terme de ce travail le participant doit être capable de : q Repérer un point de l’espace en utilisant le système de coordonnées cylindriques. q Passer des coordonnées cylindriques aux coordonnées cartésiennes q Utiliser ce système de coordonnées dans la résolution des problèmes présentant une symétrie cylindrique.

Khayar-marrakh Coordonnées cylindriques

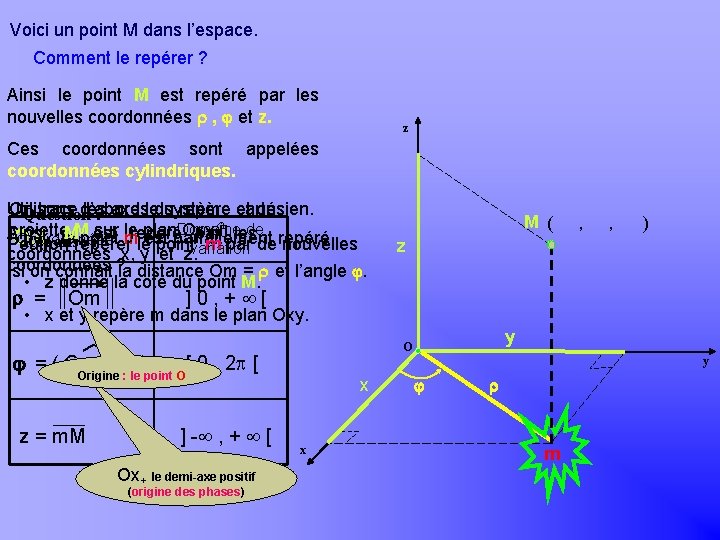
Khayar-marrakh Voici un point M dans l’espace. Comment le repérer ? Ainsi le point M est repéré par les nouvelles coordonnées , et z. z Ces coordonnées sont appelées coordonnées cylindriques. Utilisons On trace d’abord les système repère et cartésien. on Question : axesledu Domaine de projette sur le plan Oxy. les Ainsi, MMpoint est repéré par Oui , le m est parfaitement Coordonnées Réponse : Peut on repérer le pointvariation m par de repéré, nouvelles coordonnées x, y et z. coordonnées si on connait ? la distance Om = et l’angle . • z donne la cote du point M. = Om M ( , , ) z ]0, + [ • x et y repère m dans le plan Oxy. = ( Ox [ 0 , 2 p [ +, Om) Origine : le point O z = m. M ] - , + [ Ox+ le demi-axe positif (origine des phases) y O y x x m

Expressions de et en fonction de x et y. Khayar-marrakh z f ( , ) g( M , ) m y O y x Objectif : On cherche à exprimer x et y en fonction Soient les ( x , y ) m' y coordonnées de et ( , ) du point m. x m' x Dans ce triangle on a : O m Considérons le triangle rectangle Om' m.

Khayar-marrakh Surfaces de Coordonnées Définition : Une surface de coordonnée est l’ensemble de points telle que l’une des trois coordonnées est constante. Première surface de coordonnée = o ( et z varient respectivement de 0 à 2 p et de – à + ) Deuxième surface de coordonnée = o ( et z varient respectivement de 0 à + et de – à + ) Troisième surface de coordonnée z = zo ( et varient respectivement de 0 à + et de 0 à 2 p )

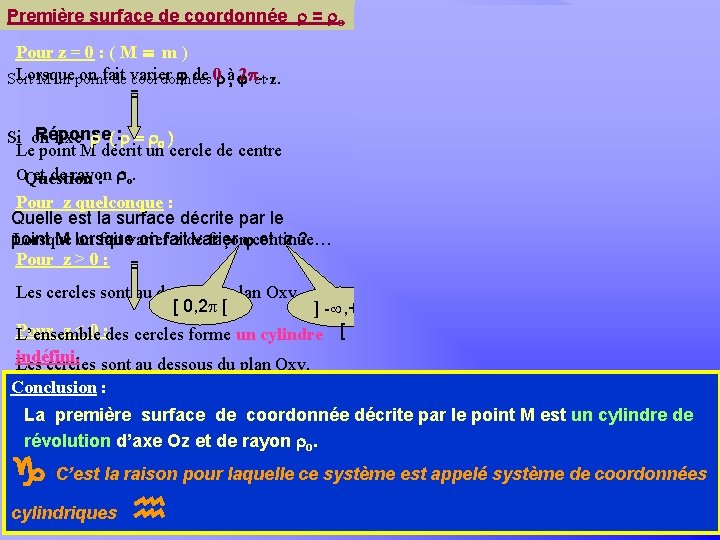
Première surface de coordonnée = o z Khayar-marrakh Pour z = 0 : ( M ≡ m ) Lorsque on fait de 0 à, 2 p… Soit M un point de varier coordonnées et z. Réponse Si on fixe ( : = o ) Le point M décrit un cercle de centre OQuestion et de rayon : o. M Pour z quelconque : Quelle est la surface décrite par le point M lorsque on fait varier et z ? Lorsque on fait varier z de façon continue… Pour z > 0 : Les cercles sont au dessus du plan Oxy. [ 0, 2 p [ ] - , + Pour z < 0 : des cercles forme un cylindre [ L’ensemble indéfini. Les cercles sont au dessous du plan Oxy. O 0 y m M x Conclusion : La première surface de coordonnée décrite par le point M est un cylindre de révolution d’axe Oz et de rayon o. C’est la raison pour laquelle ce système est appelé système de coordonnées cylindriques

Deuxième surface de coordonnée = o Khayar-marrakh Si on fixe Pour z = 0 : ( (M ≡= m o) ) Lorsque on fait varier uniquement de 0 à + … Question Réponse : : Quelle est la surface décrite par le point M fait varier de et zl’origine ? Lelorsque point Mondécrit, à partir O, une demi-droite, dans le plan Oxy, faisant un angle o avec l’axe Ox+. ] 0 , + : [ ] - , + [ Pour z quelconque Pour z > 0 : Si on fait varier z de façon continue … Les demi-droites sont au-dessus du plan Oxy z M z o Pour z < 0 : Les demi-droites sont au-dessous duun plandemi. Oxy L’ensemble des demi-droites forme plan ayant l’axe Oz pour frontière et faisant x un angle o avec l’axe Ox+. y o m Conclusion : La deuxième surface de coordonnée décrite par le point M est un demi-plan ( le méridien ) faisant un angle o avec l’axe Ox+.

Troisième surface de coordonnée Khayar-marrakh z = zo Si on fixe z ( z = zo ) Lorsque on fait varier de 0 à 2 p … z Réponse : : Question Quelle est la surface décrite par le point Lelorsque point Mon décrit M varieun cercle et ? de . centre O et de rayon r. Z o 0 O′ Maintenant, si on fait varier de façon continue … Pour d’autres [ 0 , 2 pvaleurs de , ]on 0 obtient , + [ un ensemble de[ cercles de centre O′. L’ensemble de cercles de centre O forme un disque de rayon infini plan de cote zo. O j M y m x Conclusion : La troisième surface de coordonnée décrite par le point M est un plan perpendiculaire à l’axe Oz.

Khayar-marrakh Axes de Coordonnées Définition : Un axe de coordonnées est l’intersection de deux surfaces de coordonnées, c’est-à-dire l’ensemble des points obtenus en fixant les valeurs de deux coordonnées et en laissant libre la troisième. Axe des r z = zo et = o Axe des j = o et z = zo Axe des z = o et = o

Axe des Khayar-marrakh z On trace les deux surfaces de coordonnées: Z = Zo et = o zo Leur intersection donne y O l’axe des o x Conclusion : L’ensemble des points M appartenant à l’intersection du plan, de cote zo et du demi-plan o, forme une demi-droite perpendiculaire à l’axe Oz. Cette demi-droite, ayant son origine sur Oz, est appelée axe des .

Axe des Khayar-marrakh z On trace les deux surfaces de coordonnées: = o et oo Z = Zo Zo o Leur intersection donne l’axe des x Conclusion : L’ensemble des points M appartenant à l’intersection du plan, de cote zo, et du cylindre de rayon o; forme une circonférence d’axe Oz. Ce cercle est appelé axe des . y

Axe des z Khayar-marrakh z o On trace les deux surfaces de coordonnées : = o et z = o o Leur intersection donne l’axe des z o x Conclusion : L’ensemble des points M appartenant à l’intersection du cylindre, de rayon o, et du demi-plan o, forme une droite perpendiculaire aux plans Oxy. Cette droite est appelée axe des z. y

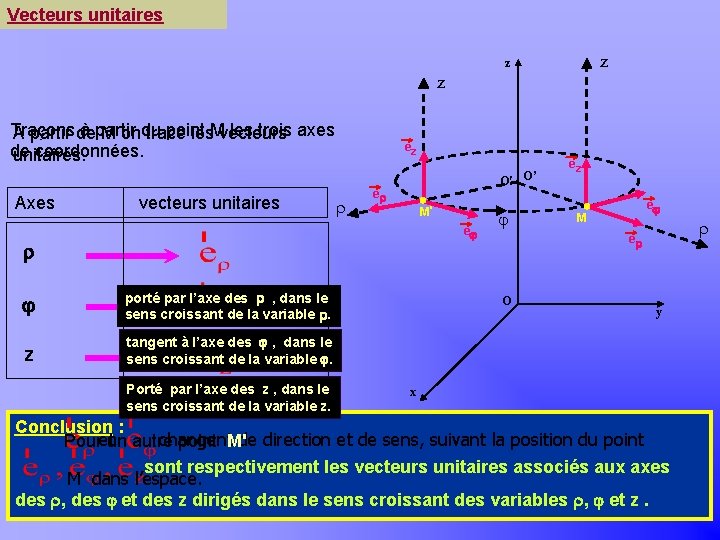
Vecteurs unitaires Khayar-marrakh z z z Traçons à partir point les trois axes A partir de M ondu trace les. Mvecteurs de coordonnées. unitaires. Axes vecteurs unitaires ez O′ O’ e M' e porté par l’axe des , dans le sens croissant de la variable . z tangent à l’axe des , dans le sens croissant de la variable . Porté par l’axe des z , dans le sens croissant de la variable z. j O ez e M e y x Conclusion : changent Pouretun autre point M'de direction et de sens, suivant la position du point sont respectivement les vecteurs unitaires associés aux axes M dans l’espace. des , des et des z dirigés dans le sens croissant des variables , et z.

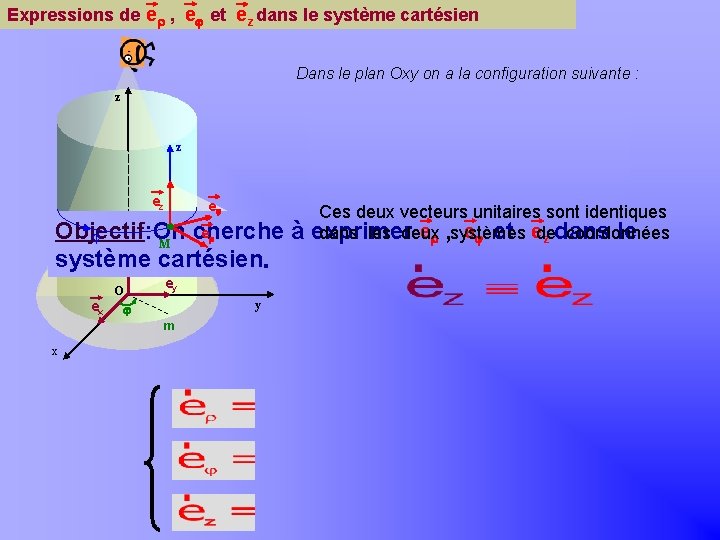
Expressions de e , e et ez dans le système cartésien Khayar-marrakh Dans le plan Oxy on a la configuration suivante : z y ez e e Objectif: On cherche à j M système cartésien. e z ey O ex y Ces deux vecteurs unitaires sont identiques Réalisons eune vue e de ede m exprimer et dessus. le dans les deux coordonnées z dans , systèmes ey j j m x ee O ex x

Déplacement élémentaire Khayar-marrakh z z + d Soient M et M deux points de l’espace. M M + d N. B. : M est infiniment voisin de M. z z + dz M O' Réponse Question : : élémentaire Le déplacement est le résultatélémentaire de MM déplacement Quelle est l’expression du vecteur trois dl =déplacements MM dans ce: système de coordonnées ? j d M 1 dz M d d M 2 O y Premier déplacement suivant l’axe des de M vers M 1 MM 1 = d x MM suivant = MMl’axe Deuxième déplacement des 1 + M 1 M 2 + M 2 M de M 1 vers M 2 M: 1 M 2 = d ou encore Troisième déplacement l’axe des z MM suivant = M 1 M 2 + MM 1 + M 2 M de M 2 vers M M 2 M = dz MM 21 + d + d M 1 M’ M 2 + d zz zz +z dz

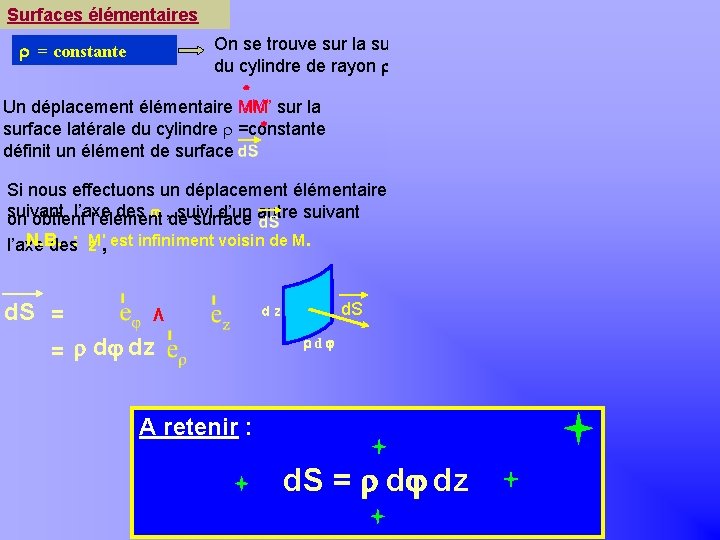
Surfaces élémentaires Khayar-marrakh On se trouve sur la surface latérale du cylindre de rayon = constante z M M' sur la Un déplacement élémentaire MM’ surface latérale du cylindre =constante définit un élément de surface Si nous effectuons un déplacement élémentaire suivant l’axe des , de suivi d’un autre suivant on obtient l’élément surface dj N. B. l’axe des: z. M', est infiniment voisin de M. d. S = Λ = d dz d. S dz O y d x A retenir : d. S = d dz d. S

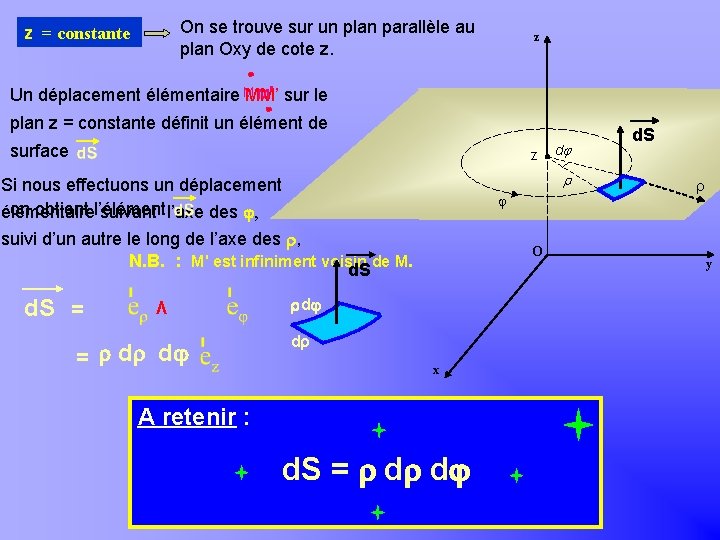
Khayar-marrakh On se trouve sur un plan parallèle au plan Oxy de cote z. z = constante z M' sur le Un déplacement élémentaire M MM’ plan z = constante définit un élément de surface z Si nous effectuons un déplacement on obtient l’élémentaire suivant l’axe des , j suivi d’un autre le long de l’axe des , N. B. : M' est infiniment voisin d. Sde M. d. S = = Λ d d dj O d d x A retenir : d. S = d d d. S y

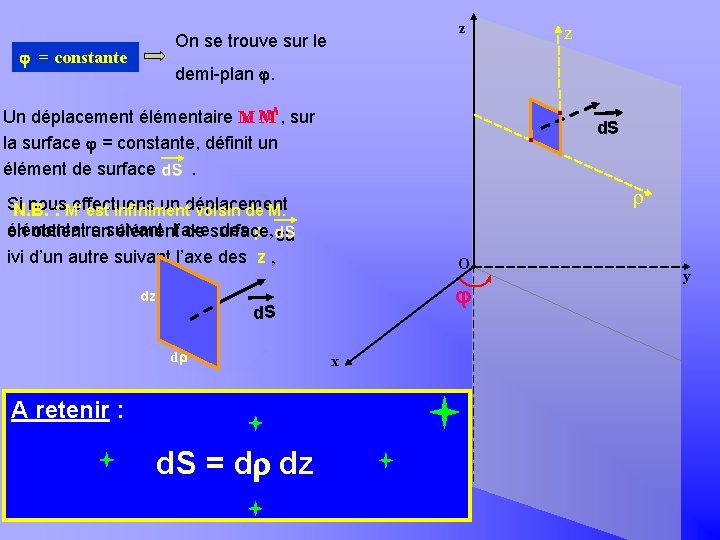
Khayar-marrakh z On se trouve sur le = constante z demi-plan . ' sur MM Un déplacement élémentaire M M', la surface = constante, définit un élément de surface. d. S Si nous effectuons un déplacement N. B. : M' est infiniment voisin de M. élémentaire des , su on obtient unsuivant élémentl’axe de surface ivi d’un autre suivant l’axe des z , O dz d. S d = Ad. S retenir : Λ = d dz d. S = d dz x y

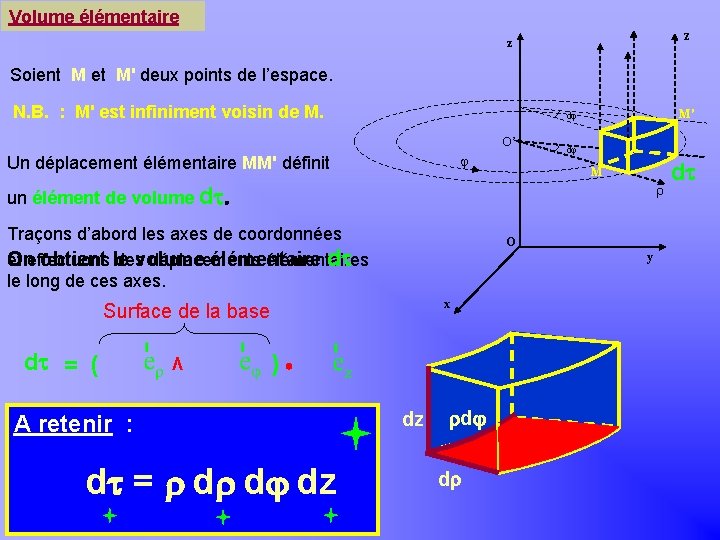
Volume élémentaire Khayar-marrakh z z Soient M et M' deux points de l’espace. N. B. : M' est infiniment voisin de M. M' dj O’ j Un déplacement élémentaire MM' définit dj M un élément de volume dt. Traçons d’abord les axes de coordonnées et effectuons des déplacements élémentaires On obtient le volume élémentaire dt le long de ces axes. O y x Surface de la base dt = ( Λ ) A retenir : d dz d = dt = d d dz dz d d dt

Nous désirons exprimer nos remerciements à tous les collègues qui, par leur aide et leur encouragement, nous ont permis d’achever ce travail. n Septembre 2006