UNIT I Formal Language and Regular Expressions Languages

UNIT - I Formal Language and Regular Expressions: Languages Definition regular expressions Regular sets identity rules. Finite Automata: DFA NFA with transitions – Significance acceptance of languages NFA to DFA conversion minimization of DFA Finite Automata with output Moore and Mealy machines Constructing finite Automata for a given regular expressions Conversion of Finite Automata to Regular expressions.

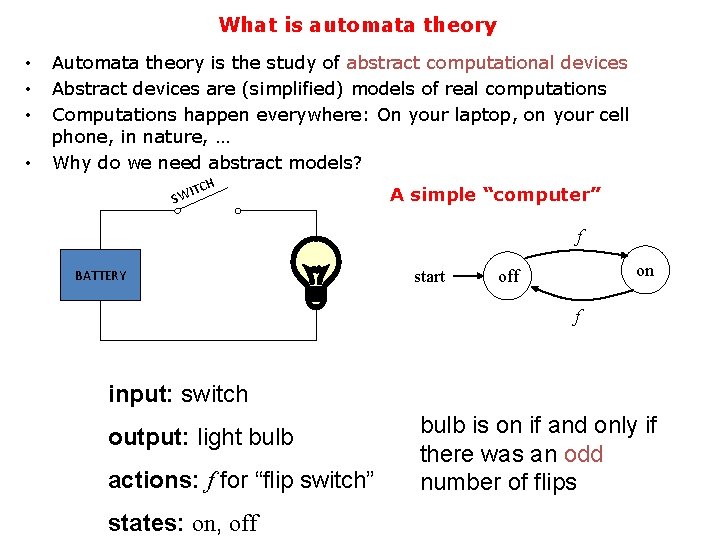
What is automata theory • • Automata theory is the study of abstract computational devices Abstract devices are (simplified) models of real computations Computations happen everywhere: On your laptop, on your cell phone, in nature, … Why do we need abstract models? H ITC SW A simple “computer” f BATTERY start on off f input: switch output: light bulb actions: f for “flip switch” states: on, off bulb is on if and only if there was an odd number of flips

Alphabets and Languages • An alphabet is a finite non-empty set. • We use the symbol ∑ (sigma) to denote an alphabet • Examples: – Binary: ∑ = {0, 1} – All lower case letters: ∑ = {a, b, c, . . z} – Alphanumeric: ∑ = {a-z, A-Z, 0 -9} – DNA molecule letters: ∑ = {a, c, g, t} Strings A string or word is a finite sequence of symbols chosen from ∑ n Empty string is (or “epsilon”) n Length of a string w, denoted by “|w|”, is equal to the number of (non - ) characters in the string n n E. g. , x = 010100 |x| = 6 n x = 01 0 1 00 |x| = ? xy = concatentation of two strings x and y

Powers of an alphabet Let ∑ be an alphabet. – ∑k = the set of all strings of length k – ∑* = ∑ 0 U ∑ 1 U ∑ 2 U … – ∑+ = ∑ 1 U ∑ 2 U ∑ 3 U … L is a said to be a language over alphabet ∑, only if L ∑* this is because ∑* is the set of all strings (of all possible length including 0) over the given alphabet ∑ Examples: 1. Let L be the language of all strings consisting of n 0’s followed by n 1’s: L = { , 01, 0011, 000111, …} 2. Let L be the language of all strings of with equal number of 0’s and 1’s: L = { , 01, 10, 0011, 1100, 0101, 1010, 1001, …} Definition: Ø denotes the Empty language n Let L = { }; Is L=Ø? 4

Formal Language A formal language L is a set of finite-length words (or "strings") over some finite alphabet A. is the empty word. Example: A = {a, b, c} L 1 = {ab, c} Some examples of formal languages: • the set of all words over {a, b}, • the set { an | n is a prime number }, • the set of syntactically correct programs in some programming language

Several operations can be used to produce new languages from given ones. Suppose L 1 and L 2 are languages over some common alphabet. • The concatenation L 1 L 2 consists of all strings of the form vw where v is a string from L 1 and w is a string from L 2. • The intersection of L 1 and L 2 consists of all strings which are contained in L 1 and also in L 2. • The union of L 1 and L 2 consists of all strings which are contained in L 1 or in L 2. • The complement of the language L 1 consists of all strings over the alphabet which are not contained in L 1. • The Kleene star L 1* consists of all strings which can be written in the form w 1 w 2. . . wn with strings wi in L 1 and n ≥ 0. Note that this includes the empty string ε because n = 0 is allowed.

Regular Expressions • A regular expression defines a regular language over an alphabet å : – Æ is a regular language: {} – Any symbol from å is a regular language: å = { a, b, c} – {a} {b} {c} Two concatenated regular languages is a regular language: å = { a, b, c} {ab} {bc} {ca} – The union (or disjunction) of two regular languages is a regular language: å = { a, b, c} {ab|bc} {ca|bb} – The Kleene closure (denoted by the Kleene star: *) of a regular language is a regular language: å = { a, b, c} {a*} {(ab|ca)*} Positive closure of a language L – • L+ = L* L 0 = L* – {e} – Parentheses group a sub-language to override operator precedence – A regular set is a set represented by a regular expression.

RE Examples • L(001) = {001} • L(0+10*) = { 0, 1, 100, 10000, … } • L(0*10*) = {1, 01, 10, 0010, …} i. e. {w | w has exactly a single 1} • L( )* = {w | w is a string of even length} • L((0(0+1))*) = { ε, 00, 01, 0000, 0001, 0100, 0101, …} • L((0+ε)(1+ ε)) = {ε, 0, 1, 01} • L(1Ø) = Ø; concatenating the empty set to any set yields the empty set. • Rε = R • R+Ø = R Exercise: Write a regular expression for the set of strings that contains an even number of 1’s over ={0, 1}. Treat zero 1’s as an even number.

Identity Rules

What are the strings represented by 10* A 1 followed by any number of 0 s (including no zeros) (10)* Any number of copies of 10 (including null string) 0 + 01 the string 0 or the string 01 0 (0 + 1)* Any string beginning with 0 (0*1)* Any string not ending with a 0 (including null string) Find a regular expression The set of bit strings with even length (00 +01 +10 +11)* Set of bit strings ending with a 0 not containing 11 not the null string (0 +10)*(0+10) or (0+10)+ The set of bit strings containing and odd number of 0 s 1*01*(01*01*)*

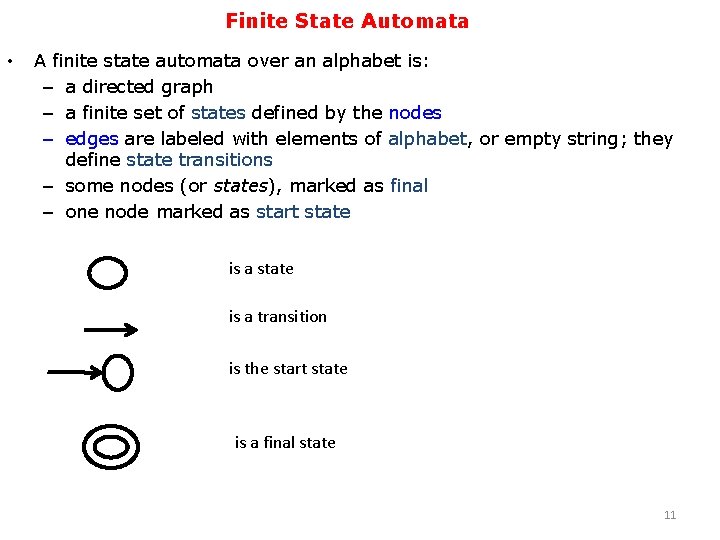
Finite State Automata • A finite state automata over an alphabet is: – a directed graph – a finite set of states defined by the nodes – edges are labeled with elements of alphabet, or empty string; they define state transitions – some nodes (or states), marked as final – one node marked as start state is a transition is the start state is a final state 11

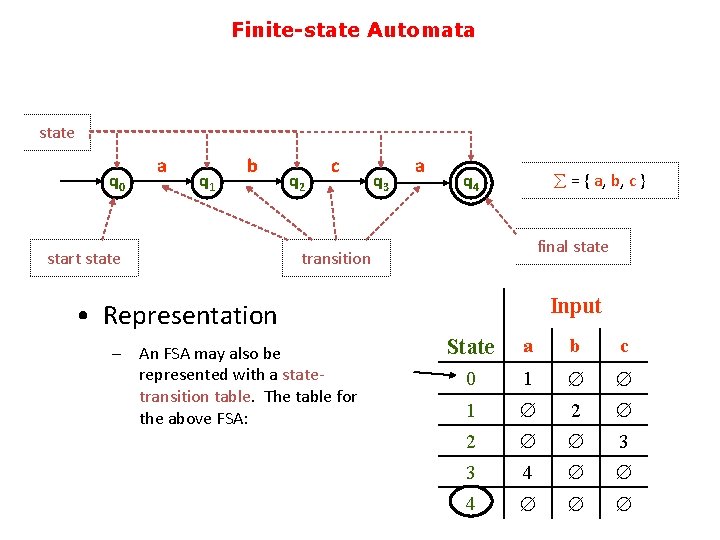
Finite-state Automata state q 0 a q 1 b start state q 2 c q 3 a å = { a, b, c } q 4 final state transition Input • Representation – An FSA may also be represented with a statetransition table. The table for the above FSA: State a b c 0 1 Æ Æ 1 Æ 2 Æ Æ 3 3 4 Æ Æ Æ

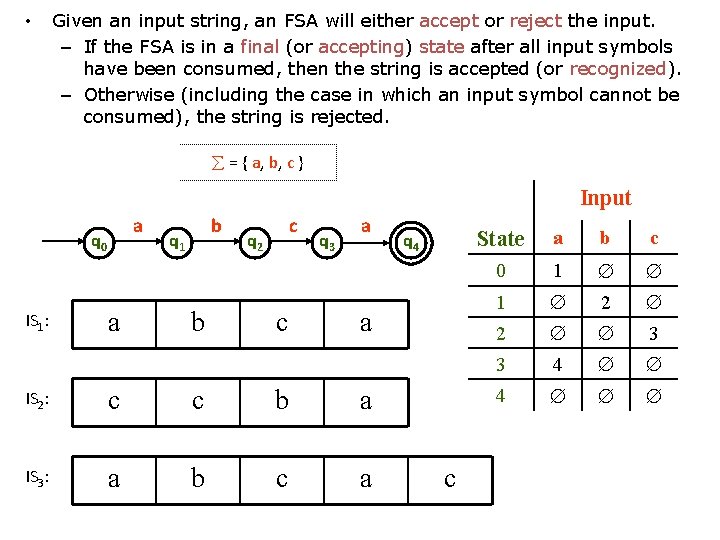
• Given an input string, an FSA will either accept or reject the input. – If the FSA is in a final (or accepting) state after all input symbols have been consumed, then the string is accepted (or recognized). – Otherwise (including the case in which an input symbol cannot be consumed), the string is rejected. å = { a, b, c } Input a q 0 IS 1: a b q 1 b c q 2 c q 3 a q 4 a IS 2: c c b a IS 3: a b c a c State a b c 0 1 Æ Æ 1 Æ 2 Æ Æ 3 3 4 Æ Æ Æ

Formal Definition of FSA A finite state automata M = (∑, Q, δ, q 0, F) ∑: alphabet Q: set of states δ: Qⅹ∑ Q, a transition function q 0: the start state F: final states • Determinism – An FSA may be either deterministic (DFSA or DFA) or non-deterministic (NFSA or NFA). • An FSA is deterministic if its behavior during recognition is fully determined by the state it is in and the symbol to be consumed. – I. e. , given an input string, only one path may be taken through the FSA. • Conversely, an FSA is non-deterministic if, given an input string, more than one path may be taken through the FSA. – One type of non-determinism is -transitions, i. e. transitions which consume the empty string (no symbols).

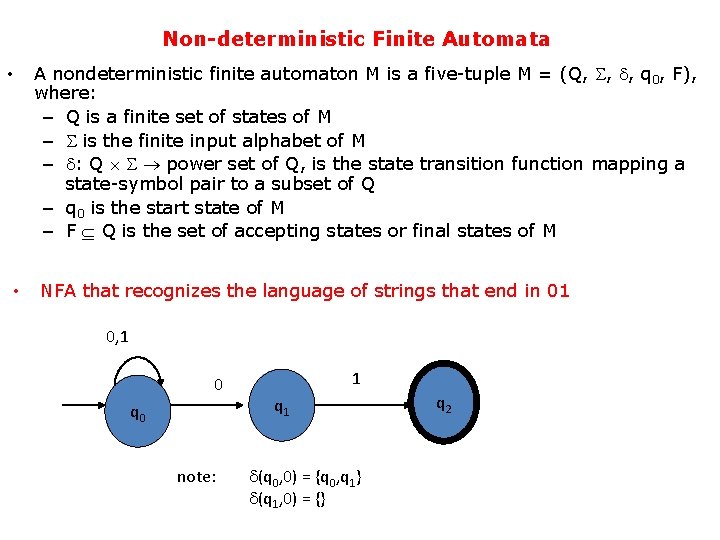
Non-deterministic Finite Automata • • A nondeterministic finite automaton M is a five-tuple M = (Q, , , q 0, F), where: – Q is a finite set of states of M – is the finite input alphabet of M – : Q power set of Q, is the state transition function mapping a state-symbol pair to a subset of Q – q 0 is the start state of M – F Q is the set of accepting states or final states of M NFA that recognizes the language of strings that end in 01 0, 1 0 q 0 note: 1 q 1 (q 0, 0) = {q 0, q 1} (q 1, 0) = {} q 2

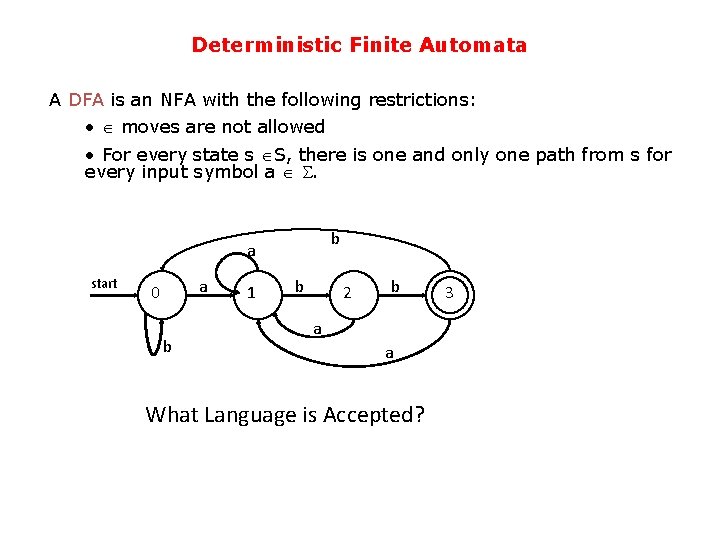
Deterministic Finite Automata A DFA is an NFA with the following restrictions: • moves are not allowed • For every state s S, there is one and only one path from s for every input symbol a . b a start a 0 b 1 b 2 b a a What Language is Accepted? 3

Algorithm to construct a NFA for any regular expression (Thompson Construction) Basic building blocks: (1) Any letter a of the alphabet is recognized by: (2) The empty set Æ is recognized by: (3) The empty string is recognized by:

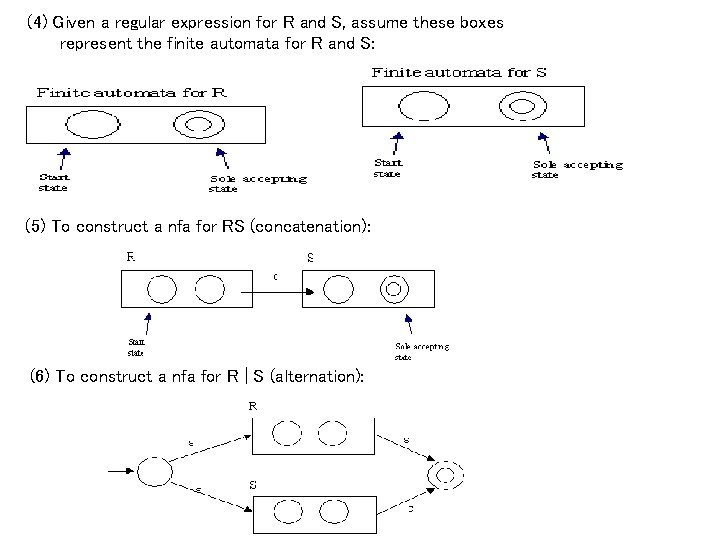
(4) Given a regular expression for R and S, assume these boxes represent the finite automata for R and S: (5) To construct a nfa for RS (concatenation): (6) To construct a nfa for R | S (alternation):

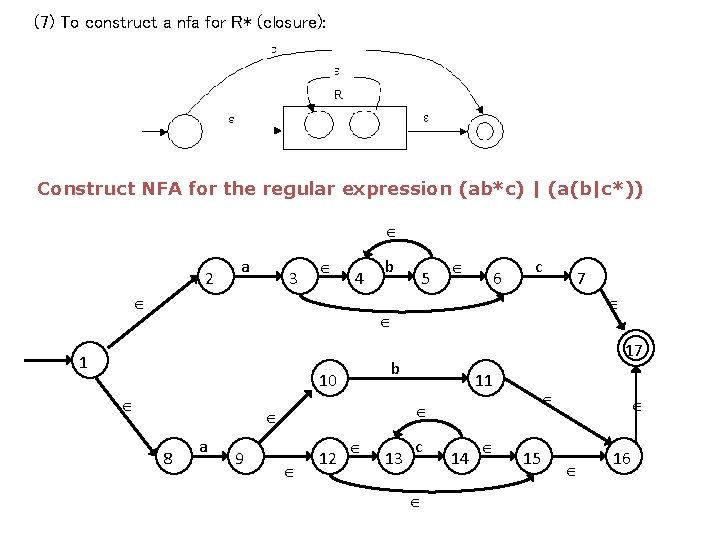
(7) To construct a nfa for R* (closure): Construct NFA for the regular expression (ab*c) | (a(b|c*)) 2 a 3 4 b 5 6 c 7 1 b 10 a 9 11 8 17 12 13 c 14 15 16

NFA to DFA conversion (Subset construction method)

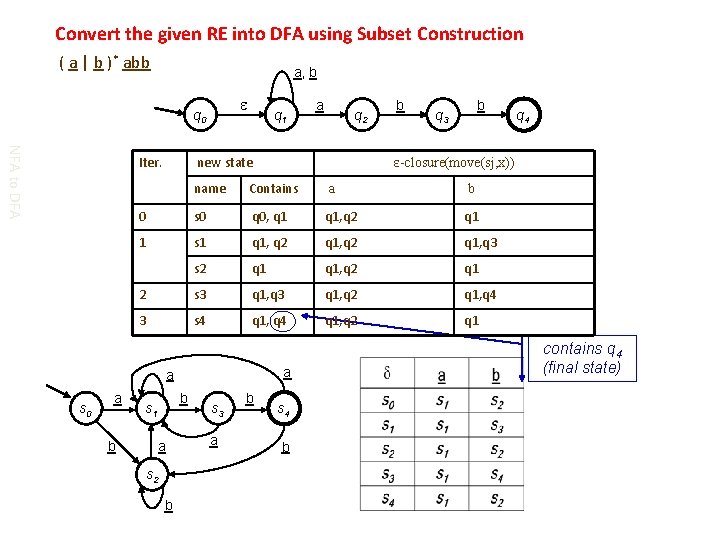
Convert the given RE into DFA using Subset Construction ( a | b )* abb a, b q 0 NFA to DFA Iter. q 1 a b q 2 new state b b q 3 Contains a b 0 s 0 q 0, q 1, q 2 q 1 1 s 1 q 1, q 2 q 1, q 3 s 2 q 1, q 2 q 1 2 s 3 q 1, q 2 q 1, q 4 3 s 4 q 1, q 2 q 1 a b s 1 a s 2 b s 3 a b q 4 ε-closure(move(sj, x)) name a s 0 a s 4 b contains q 4 (final state)

1. 2. 3. 4. Converting DFAs to REs Combine serial links by concatenation Combine parallel links by alternation Remove self-loops by Kleene closure Select a node (other than initial or final) for removal. Replace it with a set of equivalent links whose path expressions correspond to the in and out links 5. Repeat steps 1 -4 until the graph consists of a single link between the entry and exit nodes. 25

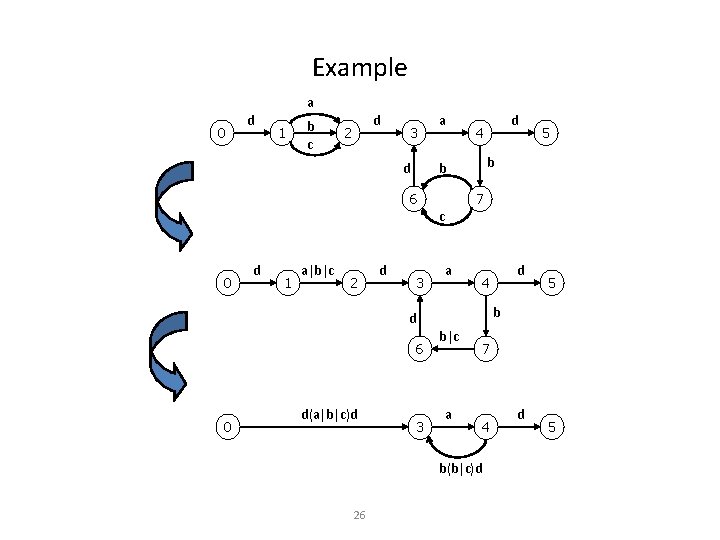
Example a 0 d 1 b c d 2 3 d a 5 b b 6 d 4 7 c 0 d 1 a|b|c 2 d 3 a 4 0 d(a|b|c)d 3 b|c a b(b|c)d 26 5 b d 6 d 7 4 d 5

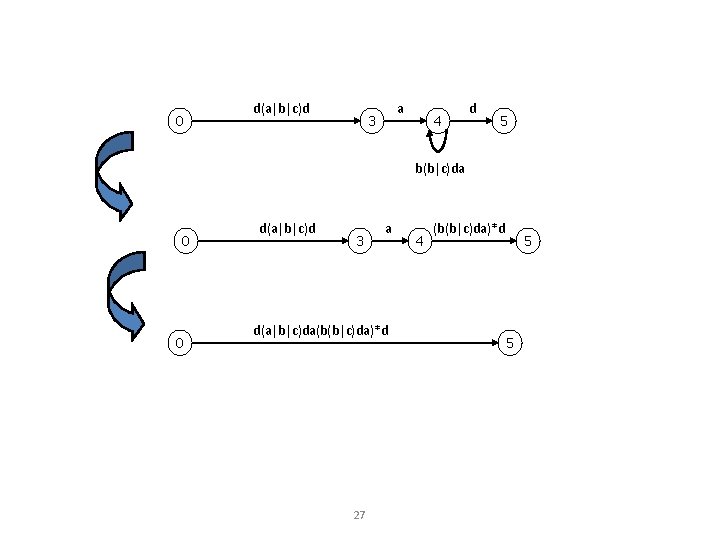
0 d(a|b|c)d a 3 4 d 5 b(b|c)da 0 0 d(a|b|c)d 3 a d(a|b|c)da(b(b|c)da)*d 27 4 (b(b|c)da)*d 5 5