Formal Languages and Automata http mail im tku

形式語言 Formal Languages and Automata 淡江大學 資訊管理系 侯 永 昌 http: //mail. im. tku. edu. tw/~ychou ftp: //mail. im. tku. edu. tw/Prof_Hou

教科書：An Introduction to Formal Languages and Automata, 5 th Edition, by Peter Linz, Jones & Bartlett Learning 出版，開發圖書總經銷 淡江大學資訊管理系侯永昌 1

第四章 規律語言的特性 (Properties of Regular Languages)

Closure Properties § 定理：If L 1 and L 2 are regular languages, then so are L 1 L 2, L 1 L 2, L 1*. We say that the family of regular languages is closed under union, intersection, concatenation, complementation, and star-closure § 例：證明規律語言的差集也有封閉性 解：L 1 L 2 = L 1 L 2，如果 L 2 是規律語言， 則 L 2 也是規律語言，而規律語言的交集也是 規律語言，因此 L 1 L 2 也是規律語言，因此 規律語言的差集也有封閉性 淡江大學資訊管理系侯永昌 3

Closure Properties § Suppose and are alphabets. Then the function h : * is called a homomorphism. In words, a homomorphism is a substitution in which a single letter is replaced with a string § If w = a 1 a 2 … an, then h(w) = h(a 1) h(a 2) … h(an) § If L is a language on , then the homomorphic image is defined as h(L) = {h(w) : w L} 淡江大學資訊管理系侯永昌 4

Closure Properties § 例：Let = {a, b} and = {a, b, c} and define h by h(a) = ab, h(b) = bbc. Then h(aba) = abbbcab. The homomorphic image of L = {aa, aba} is the language h(L) = {abab, abbbcab} § 例：Take = {a, b} and = {b, c, d} and define h by h(a) = dbcc, h(b) = bdc. If L is the regular language denoted by r = (a + b*)(aa)*, then r 1 = (dbcc + (bdc)*) (dbcc)* denotes the regular language h(L) 淡江大學資訊管理系侯永昌 5

Closure Properties § 定理：Let h be a homomorphism. If L is a regular language, then its homomorphic image h(L) is also regular. The family of regular languages is therefore closed under arbitrary homomorphisms § Let L 1 and L 2 be languages on the same alphabet. Then the right quotient of L 1 with L 2 is defined as L 1/L 2 = {x : xy L 1 for some y L 2} 淡江大學資訊管理系侯永昌 6

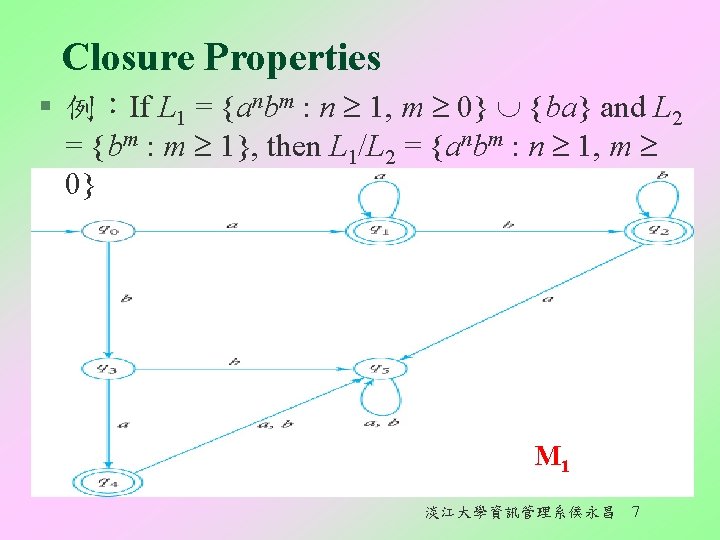
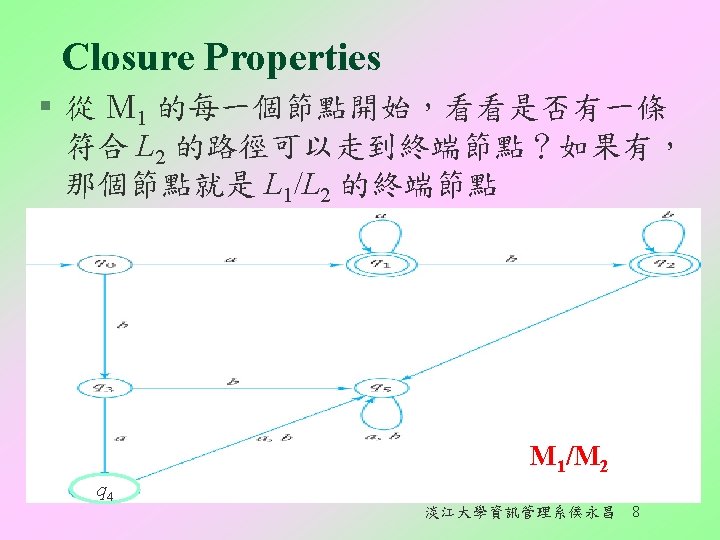
Closure Properties § 例：If L 1 = {anbm : n 1, m 0} {ba} and L 2 = {bm : m 1}, then L 1/L 2 = {anbm : n 1, m 0} M 1 淡江大學資訊管理系侯永昌 7

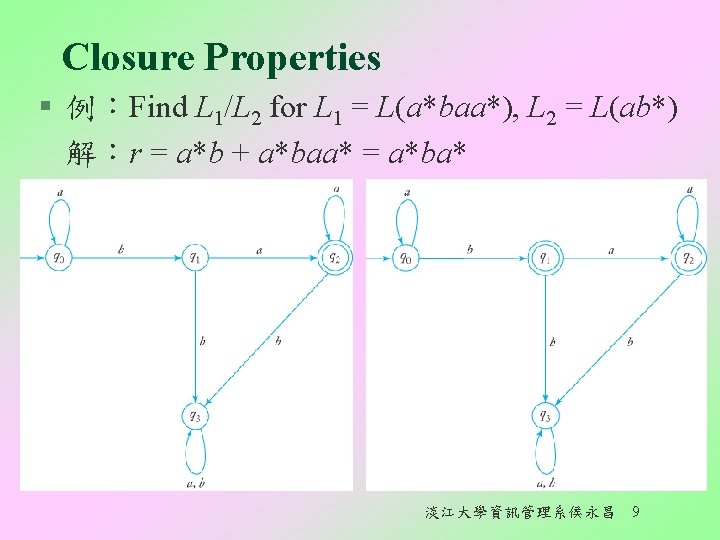
Closure Properties § 例：Find L 1/L 2 for L 1 = L(a*baa*), L 2 = L(ab*) 解：r = a*b + a*baa* = a*ba* 淡江大學資訊管理系侯永昌 9

Closure Properties § 定理：If L 1 and L 2 are regular languages, then L 1/L 2 is also regular. We say that the family of regular languages is closed under right quotient with a regular language 淡江大學資訊管理系侯永昌 10

Questions about Regular Languages § 定理：Given a standard representation of any regular language L on and any w *, there exists an algorithm for determining whether or not w is in L § 定理：There exists an algorithm for determining whether a regular language, given in standard representation, is empty, finite, or infinite § 定理：Given standard representations of two regular languages L 1 and L 2, there exists an algorithm to determine whether or not L 1 = L 2 淡江大學資訊管理系侯永昌 11

Pumping Lemma § 定理：Let L be an infinite regular language. Then there exists some positive integer m such that any w L with |w| m can be decomposed as w = xyz with |xy| m, and |y| 1, such that wi = xyiz is also in L for all i = 0, 1, 2, … § 也就是說： regular language L 中一個夠長的字 串都可以被分割成三段 (xyz)，任意重複中間 的那一段 (y)，所形成的新字串 (xyiz)，也都是 L中的一個合法字串 淡江大學資訊管理系侯永昌 14