Unidad Didctica Electrnica Digital 4 ESO Guin electrnica

Unidad Didáctica Electrónica Digital 4º ESO

Guión electrónica digital Sistemas analógicos y digitales Sistemas de numeración Sistemas binarios Álgebra de Boole Puertas lógicas Diseño y simplificación de funciones lógicas Miniterms Maxiterms

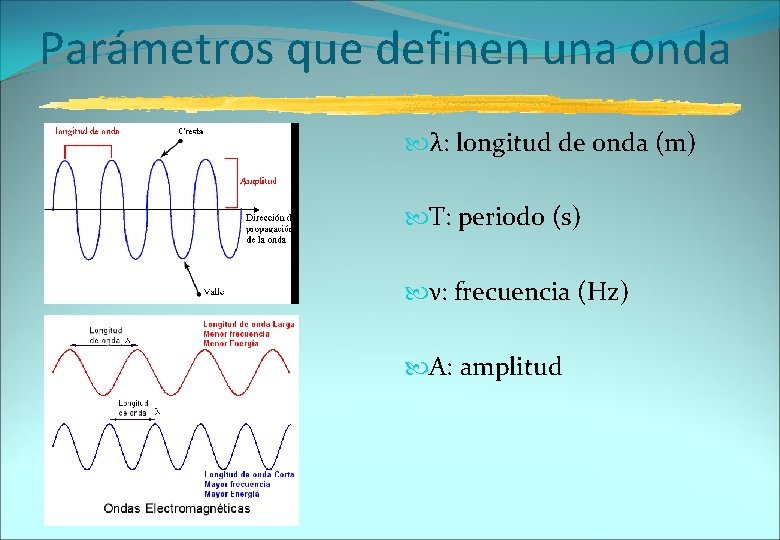
Parámetros que definen una onda λ: longitud de onda (m) T: periodo (s) ν: frecuencia (Hz) A: amplitud

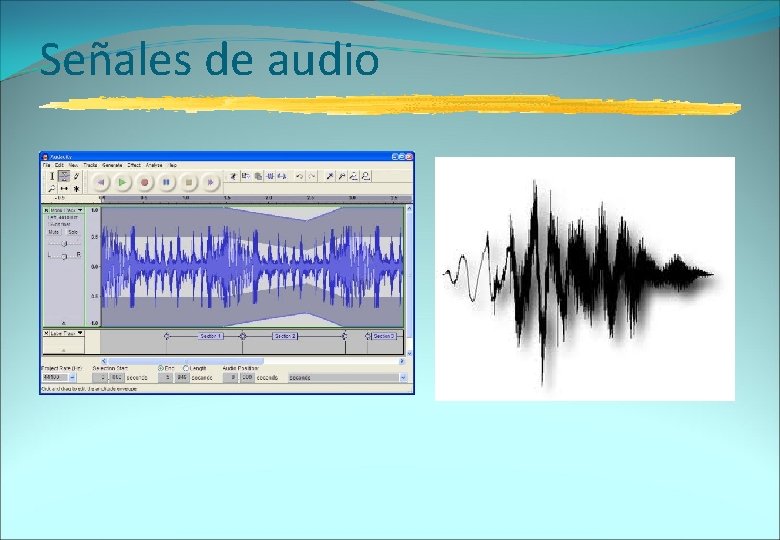
Señales de audio

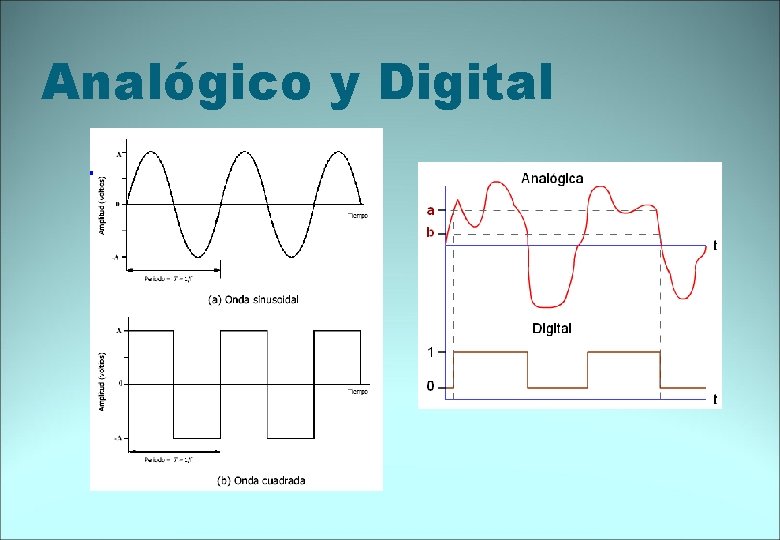
Analógico y Digital

Sistemas digitales Son sistemas que trabajan con valores discretos en el tiempo (no continuos), puntos. Estos puntos, se representan con números El código numérico que emplean los sistemas digitales el código binario, con sus propias reglas y álgebra.

Sistema de numeración binario Un sistema numérico es la forma de representar un magnitud cuantitativa mediante símbolos. Un número es una sucesión de símbolos El sistema de numeración binario utiliza dos símbolos para representar magnitudes cuantitativas : 0 y 1. Ejemplo: Sistema decimal: 1375 Sistema binario: 100010

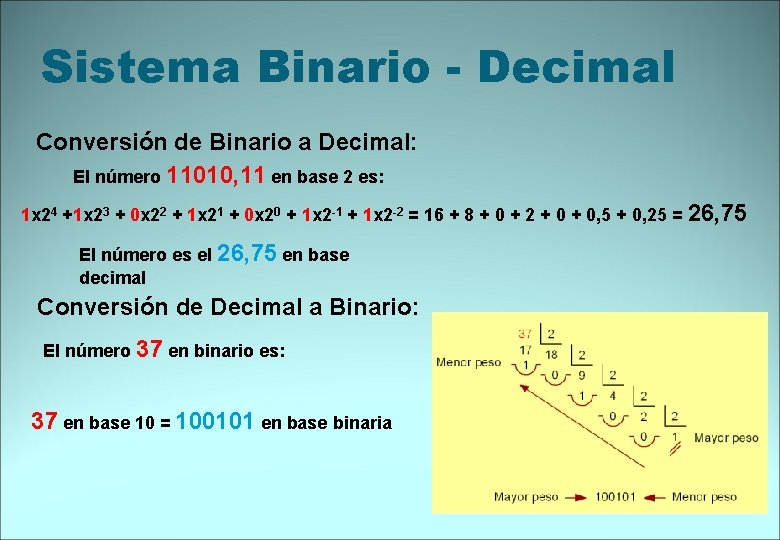
Sistema Binario - Decimal Conversión de Binario a Decimal: El número 11010, 11 en base 2 es: 1 x 24 +1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 + 1 x 2 -1 + 1 x 2 -2 = 16 + 8 + 0 + 2 + 0, 5 + 0, 25 = El número es el 26, 75 en base decimal Conversión de Decimal a Binario: El número 37 en binario es: 37 en base 10 = 100101 en base binaria 26, 75

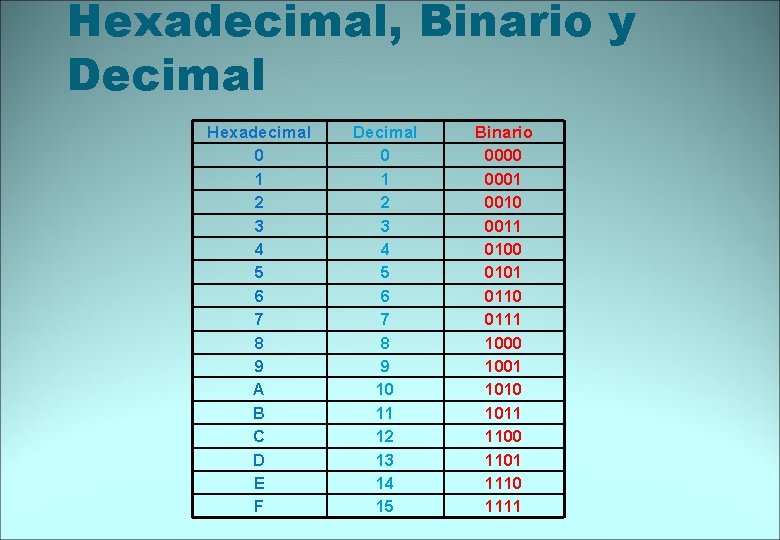
Hexadecimal, Binario y Decimal Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Binario 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Álgebra de Boole La forma de operar magnitudes en el sistema de numeración binario es el álgebra de Boole. Sus operaciones y postulados son: a+0=a a+1=1 Operaciones a+a=a Suma S=a+b a+ā=1 a· 0=0 a· 1=a a·a=a a·ā=0 Producto S=a· b Complementación o inversión S=ā ā=a

Propiedades del álgebra de Boole 1 ) Conmutativa • a+b = b+a • a·b = b·a 2 ) Asociativa • a+b+c = a+(b+c) • a·b·c = a·(b·c) 5 ) Elemento absorbente • a+1 = 1 • a· 0 = 0 6 ) Ley del complementario • a+ā = 1 • a·ā = 0 7 ) Idempotente • a+a = a • a·a = a 3 ) Distributiva • a·(b+c) = a·b + a. c • a+(b·c) = (a+b)·(a+c) ¡ojo! 4 ) Elemento neutro • a+0 = a • a· 1 = a 8 ) Simplificativa • a+a·b = a • a·(a+b) = a 9 ) Teoremas de Demorgan • •

Puertas lógicas básicas Funciones Suma (OR): S=a+b Multiplicación (AND): S=a·b Inversor Negación (¯): S=ā Tabla de verdad b a S = a+b 00 01 10 11 0 1 1 1 b a S = a·b 00 01 10 11 0 0 0 1 a S=ā 0 1 1 0 Símbolos antiguos

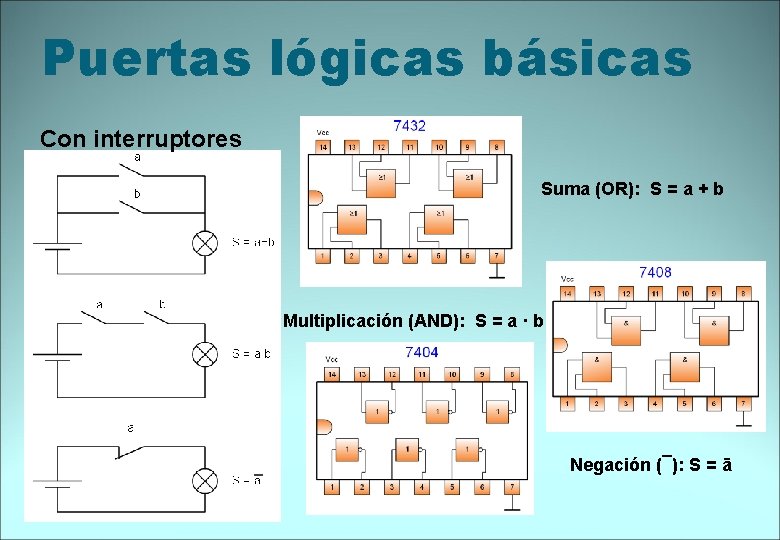
Puertas lógicas básicas Con interruptores Suma (OR): S = a + b Multiplicación (AND): S = a · b Negación (¯): S = ā

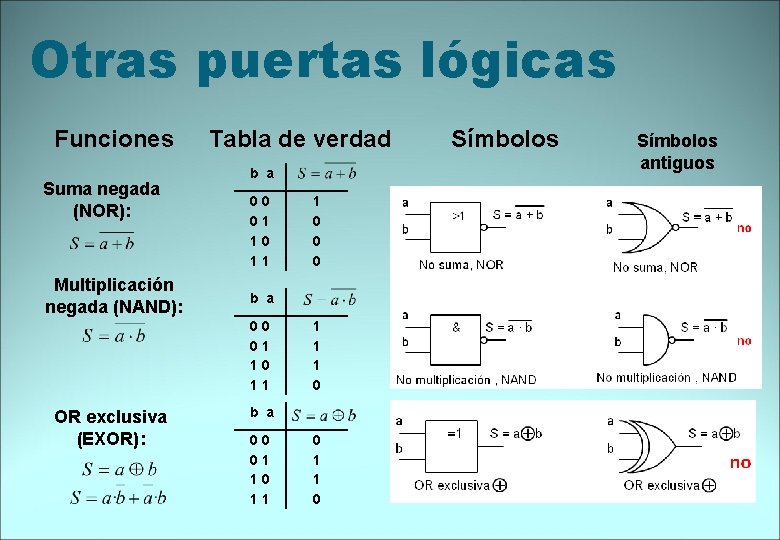
Otras puertas lógicas Funciones Suma negada (NOR): Multiplicación negada (NAND): Tabla de verdad b a 00 01 10 11 OR exclusiva (EXOR): 1 0 0 0 1 1 1 0 b a 00 01 10 11 0 1 1 0 Símbolos antiguos

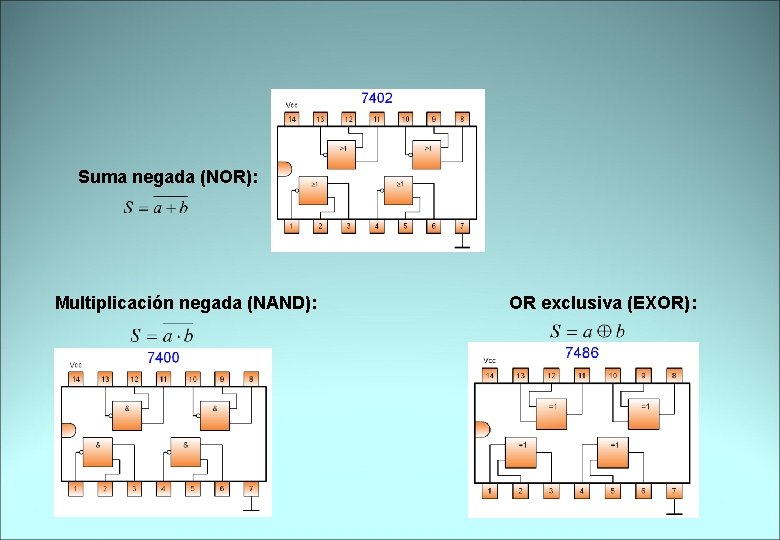
Suma negada (NOR): Multiplicación negada (NAND): OR exclusiva (EXOR):

Funciones lógicas Una función lógica representa la forma de combinar las señales de las entradas lógicas(0 ó 1) para obtener la salida deseada. Esta combinación de entradas se expresa matemáticamente en binario, realizando operaciones lógicas con las entradas ¿Esto para qué sirve? Para resolver problemas del siguiente tipo: Diseña un circuito de apertura de una puerta de seguridad que se abra cuando el director de la empresa y el encargado introduzcan el código.

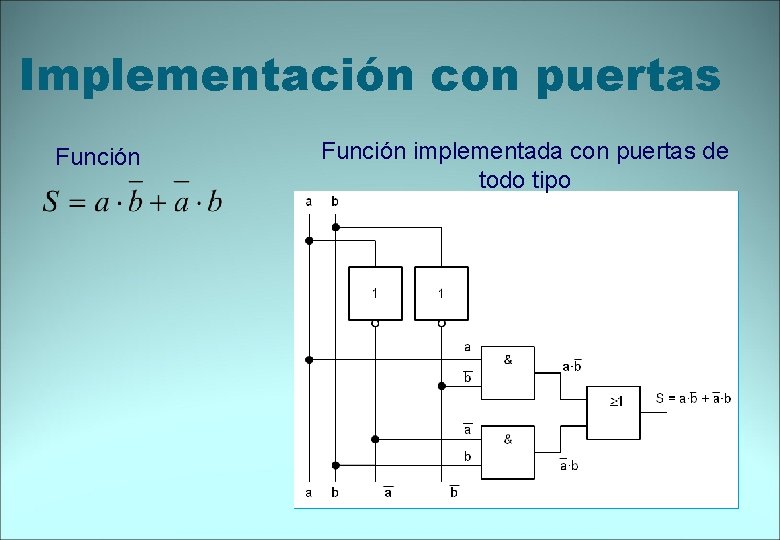
Funciones lógicas. Simplificación por propiedades Función lógica Propiedad Distributiva, agrupamos términos en parejas con el mayor número posible de variables iguales. Ley del complementario Elemento neutro

Implementación con puertas Función implementada con puertas de todo tipo

Tabla de verdad La tabla de verdad es un representación gráfica donde aparecen todas las combinaciones de las variables de entrada y el valor de la salida. El número de combinaciones de entrada es 2 , donde n es el número de variables de entrada. n El número binario que representan las combinaciones de las variables de entrad, tiene que colocarse en orden ascendente. La salida viene determinada por las condiciones del circuito

Funciones lógicas. Tabla de verdad A partir de una situación real obtenemos la tabla de verdad y a partir de ésta, obtenemos la función lógica y el circuito electrónico digital Si partimos de la función lógica, dando valores a cada variable, y operando como indica la función lógica, obtenemos la tabla de verdad. a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 S 0 1 1 0 0 1

Función lógica a partir de la tabla de verdad Se puede obtener de dos formas, como suma de productos cuya salida sea 1 (Miniterms) o como producto de sumas cuya salida sea 0(Maxiterms). La función obtenida se denomina forma canónica y normalmente hay que simplificarla. Tabla de verdad a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 S 0 1 1 0 0 1 Por Miniterms Por Maxiterms

Mapas de Karnaugh Método para simplificar la función canónica Primero hay que dibujar la tabla, con las variables de entrada siguiendo un código Gray Después rellenar la cuadrícula con los valores de la salida según indica la tabla de verdad.

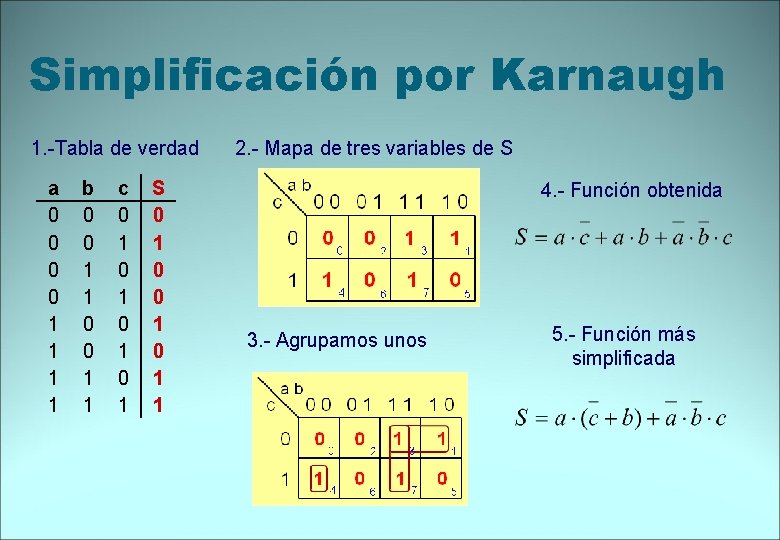
Simplificación por Karnaugh Se dibuja el mapa de Karnaugh y se rellena con “ 1” , si utilizamos la forma canónica por miniterms, siguiendo la tabla n de verdad. Se agrupan los “ 1” en grupos de 2 , es decir, 1, 2, 4, 8. . Formas de agrupar: Se forman grupos lo más grande posible Se pueden agrupar aristas y esquinas Cada 1 puede pertenecer a más de un grupo Para construir la función, de cada grupo se toma la variable que no cambia de valor.

Simplificación por Karnaugh 1. -Tabla de verdad a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 S 0 1 0 1 1 2. - Mapa de tres variables de S 4. - Función obtenida 3. - Agrupamos unos 5. - Función más simplificada

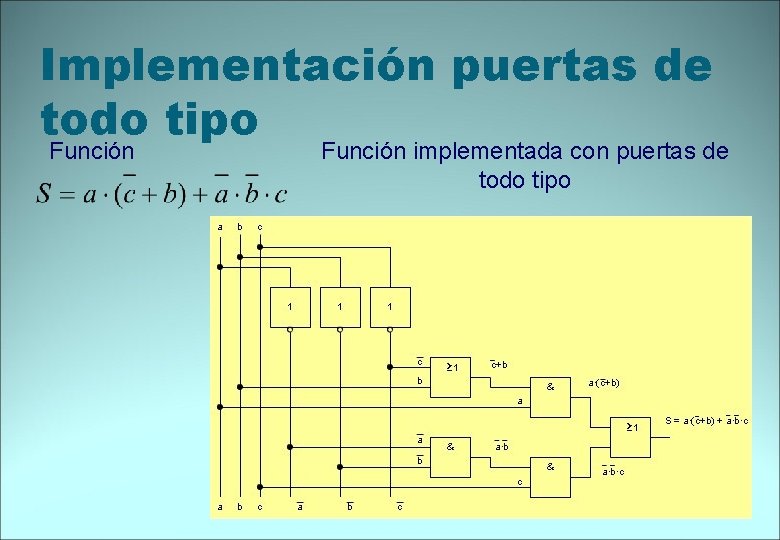
Implementación puertas de todo tipo Función implementada con puertas de todo tipo

Resolución de problemas Pasos a seguir: 1. - Identificar las entradas y salidas 2. - Crear la tabla de verdad 3. - Obtener la función simplificada 4. - Implementar la función con puertas de todo tipo, puertas NAND y puertas NOR

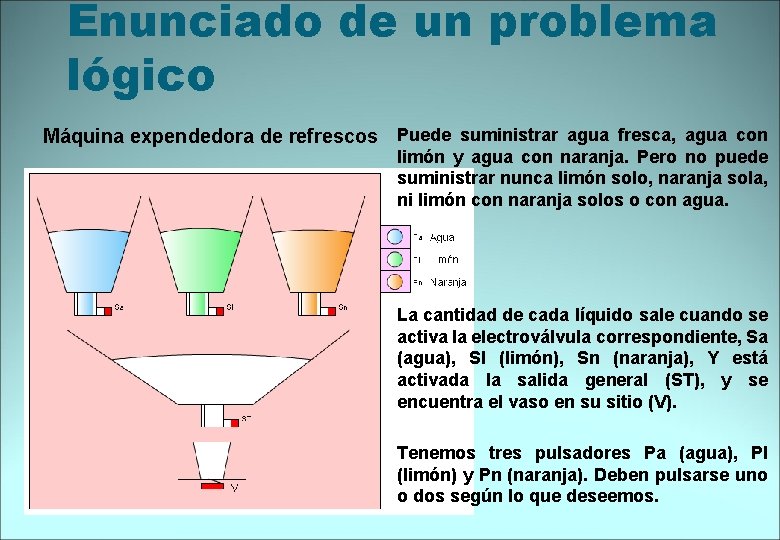
Enunciado de un problema lógico Máquina expendedora de refrescos Puede suministrar agua fresca, agua con limón y agua con naranja. Pero no puede suministrar nunca limón solo, naranja sola, ni limón con naranja solos o con agua. La cantidad de cada líquido sale cuando se activa la electroválvula correspondiente, Sa (agua), Sl (limón), Sn (naranja), Y está activada la salida general (ST), y se encuentra el vaso en su sitio (V). Tenemos tres pulsadores Pa (agua), Pl (limón) y Pn (naranja). Deben pulsarse uno o dos según lo que deseemos.

Identificar entradas y salidas 1. - Identificar las entradas y salidas Entradas, serán los pulsadores Pa, Pl, Pn y el sensor que detecta la presencia del vaso V. Pulsador pulsado será “ 1” y no pulsado será “ 0” Salidas, serán todas las electroválvulas sobre las que hay que actuar, Sa, Sl, Sn y ST. Cuando la electroválvula en cuestión valga “ 1” permitirá que salga la cantidad de líquido necesario

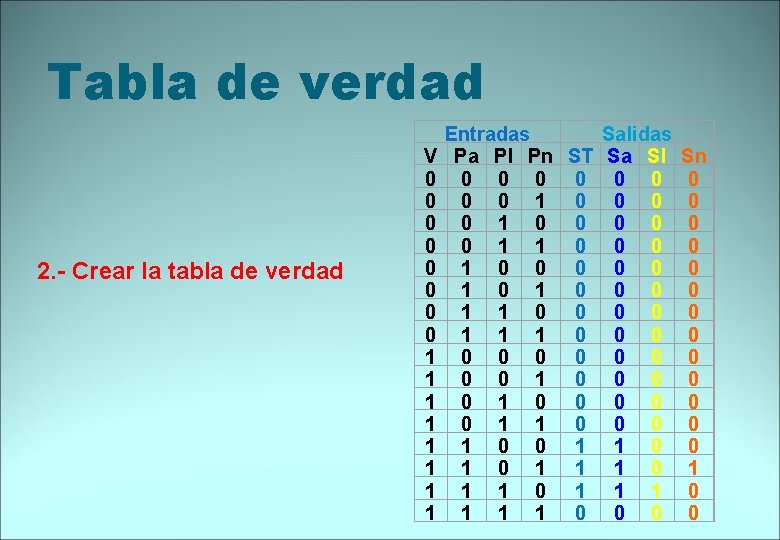
Tabla de verdad 2. - Crear la tabla de verdad V 0 0 0 0 1 1 1 1 Entradas Salidas Pa Pl Pn ST Sa Sl Sn 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 1 1 0 0

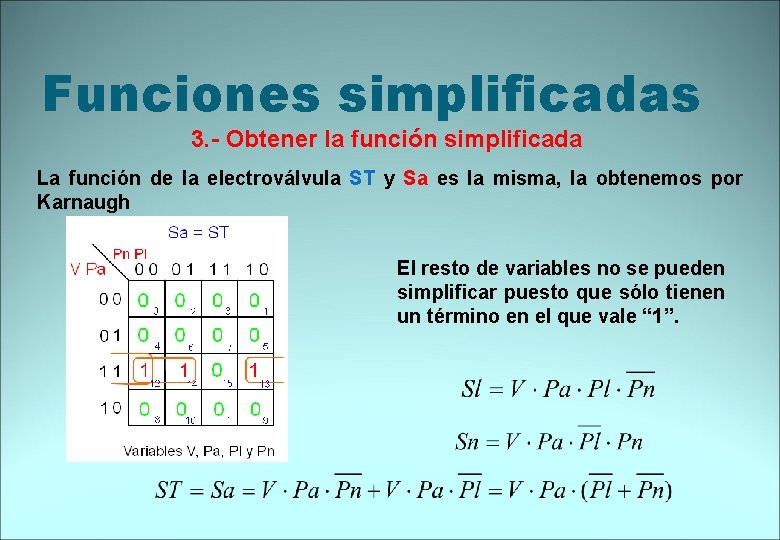
Funciones simplificadas 3. - Obtener la función simplificada La función de la electroválvula ST y Sa es la misma, la obtenemos por Karnaugh El resto de variables no se pueden simplificar puesto que sólo tienen un término en el que vale “ 1”.

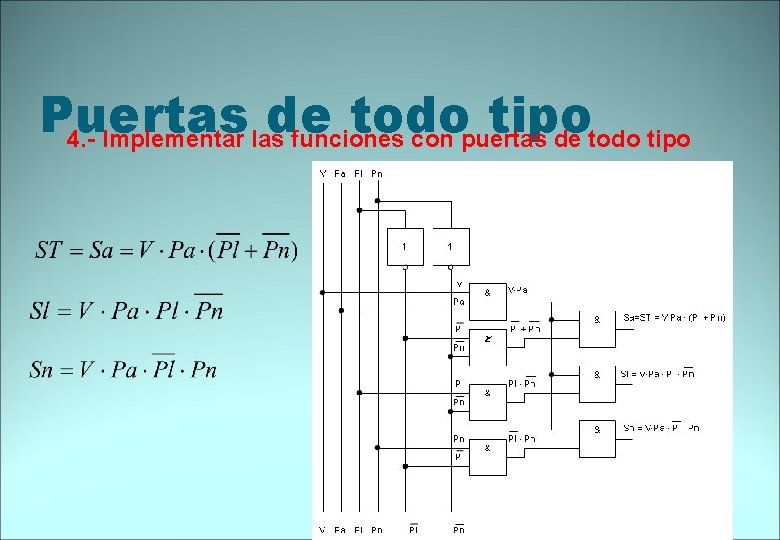
Puertas de todo tipo 4. - Implementar las funciones con puertas de todo tipo

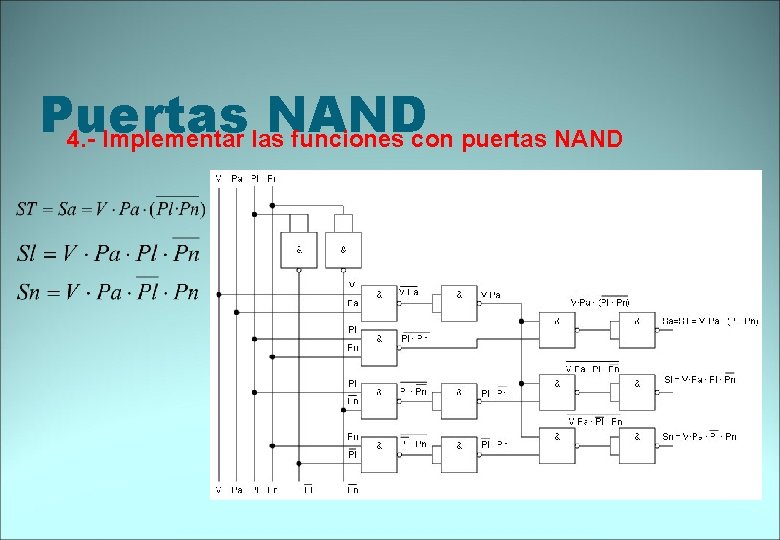
Puertas NAND 4. - Implementar las funciones con puertas NAND

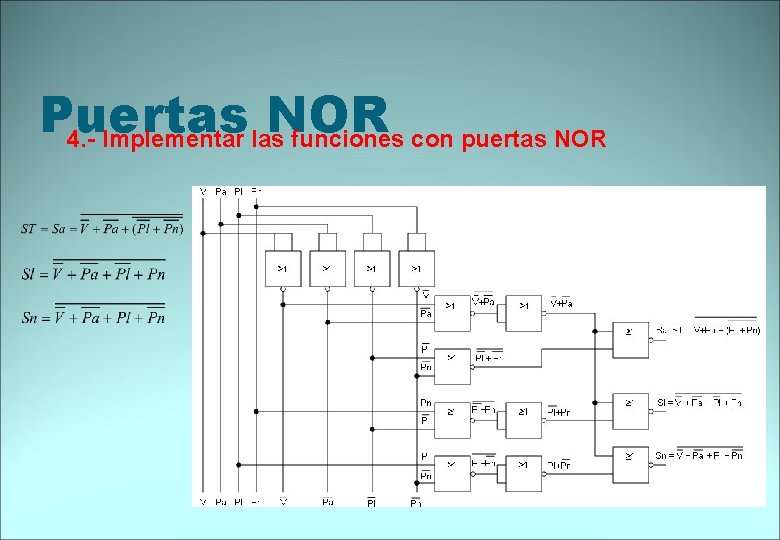
Puertas NOR 4. - Implementar las funciones con puertas NOR