Un estudio de los polinomios ortogonales asociados con

Un estudio de los polinomios ortogonales asociados con el oscilador armónico cuántico sobre espacios de curvatura constante Christophe Vignat y PWL

Contextos l Estudio de Haces Lorentzianos Estudio de soluciones de la Ec. de Schödinger para potencial del tipo Pochl-Teller l potencial anarmónico • Información de Fisher, entropía, . . . evaluadas para funciones especiales (física atómica).

Oscilador harmónico cuántico relativista V. Aldaya, J. Bisquert y J. Navarro-Salas (1991) • Dificultades en la generalización de cualquier ecuación cuántica para estados ligados al caso relativista. Una posibilidad (naif) Conduce a funciones de onda que tienen una dependencia temporal Gaussiana y la dependencia espacial dada por los polinomios de Hermite Aldaya et. al. usan los operadores energía, posición y momento No relativista

Estados cuánticos Por ejemplo: donde Los estados excitados son de la forma: donde son los polinomios de Hermite relativistas Existe una restricción sobre N>-1/2!!

El estado fundamental es Esta función es una q-gaussiana!! Las funciones verifican la ecuación de Klein-Gordon asociada con la métrica anti-de Sitter: Los polinomios fueron relacionados con los polinomios de Gegenbauer los cuales, a su vez son un caso particular de los polinomios de Jacobi.

Polinomios de Gegenbauer Polinomios de Hermite extendidos donde para y cuando Tanto los polin. de Gegenbauer como los de Hermite extendidos son ortogonales con respecto a medidas no usuales. Aparecen como solución de la ec. de Schrödinger asociada al potencial de Pöschl-Teller

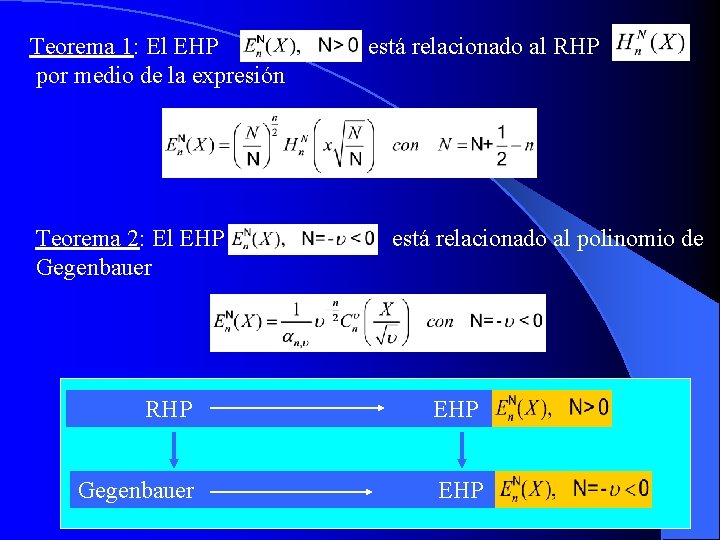
Teorema 1: El EHP por medio de la expresión Teorema 2: El EHP Gegenbauer está relacionado al RHP está relacionado al polinomio de RHP EHP Gegenbauer EHP

Correspondencia Geométrica: Conjunto de funciones ortogonales: A partir de ellas construimos las correspondientes densidades de probabilidad: Teorema: Si X (variable aleatoria) se distribuye de acuerdo a entonces se distribuye de acuerdo a

La inversa de (*) es Proyección gnomonica Extensión al oscilador armónico sobre una esfera y sobre el plano hiperbólico Esfera 2 D Plano Euclídeo Plano hiperbólico Tres casos con curvatura (como parámetro) constante (k>0, k=0 y k<0) R Usando coord. (R, ) el elem. de línea

El Lagrangeano de un oscilador armónico sobre alguno de estos espacios es: De este modo el potencial del oscilador armónico, para cada caso, es Cambios de variables: Coord. Cartesianas:

Teorema: Consideremos el oscilador armónico sobre el plano hiperbólico descripto por sus coordenadas (x, ) y cos densidad de probabilidad Si este sistema es transformado como entonces el nuevo sistema tiene densidad de probabilidad dada por

Un enfoque entrópico: Entropía de Tsallis distribución de probabilidad En el caso q=1, la distribución con máxima entropía y dada variancia es la Gaussiana: Las funciones de Hermite están definidas como En el caso q<1 las distribuciones canónicas son las q-Gaussianas

• La densidad de probabilidad que describe el oscilador armónico sobre una superficie de curvatura constante donde Polinomios de Gegenbauer • El oscilador armónico en el contexto relativista tiene densidad de probabilidad El comportamiento del oscilador armónico, tanto en el caso relativista Como en el caso de espacios de curvatura constante pueden contextualizarse En el marco del formalismo no extensivo