Tutorial Reminder Please download the tutorial from the

Tutorial Reminder Please download the tutorial from the course web page and try them out Tutorial class will be conducted on 12 DEC 03 (Friday) Submit solutions for PROBLEMS (1), (2), (7) and (9) to your tutors [NOT Conceptual questions] Tutors will discuss the solutions with you Password to solution 1 will be provided after the tutorial class 1

Recap The length of a body measured at rest = proper length L = improper length = length of an object when it’s in relative motion wrp to the observer Length contraction, L = L’/g, L’ = proper length 2

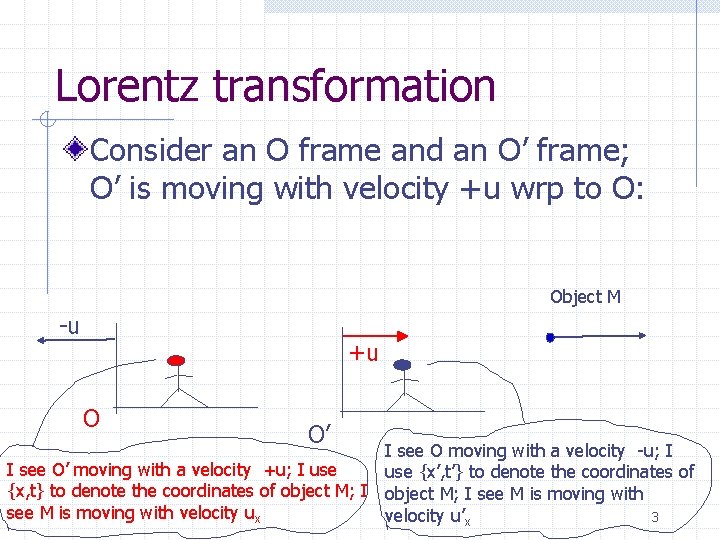
Lorentz transformation Consider an O frame and an O’ frame; O’ is moving with velocity +u wrp to O: Object M -u +u O O’ I see O moving with a velocity -u; I I see O’ moving with a velocity +u; I use {x’, t’} to denote the coordinates of {x, t} to denote the coordinates of object M; I see M is moving with velocity ux 3 velocity u’x

Lorentz transformation relates {x’, t’} {x, t}; u’x ux 4

Example Two events are seen to be occurring at the same point in a rest frame O. t 12 O u O’ The two events are denoted as t 1 , t 2 such that Dt = t 2 - t 1 = 1 s, and Dx =0. In the moving frame O’, what is the time interval between the two events? 5

The time t’ as seen by O’ in terms of t is simply related by Hence the time interval in O’, Dt’ in terms of Dt is simply This is nothing but just the time dilation effect 6

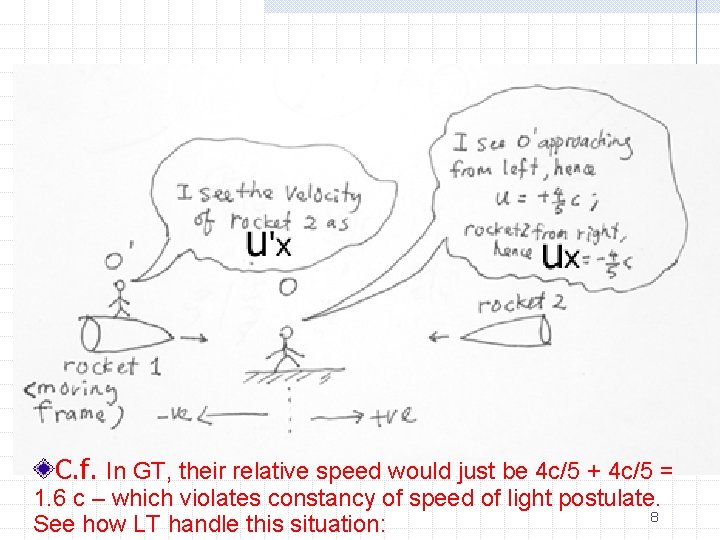
Example (relativistic velocity addition) Rocket 1 is approaching rocket 2 on a head-on collision course. Each is moving at velocity 4 c/5 relative to an independent observer midway between the two. With what velocity does rocket 2 approaches rocket 1? 7

C. f. In GT, their relative speed would just be 4 c/5 + 4 c/5 = 1. 6 c – which violates constancy of speed of light postulate. 8 See how LT handle this situation:

Choose the observer in the middle as in the stationary frame, O Choose rocket 1 as the moving frame O‘ Call the velocity of rocket 2 as seen from rocket 1 u’x. This is the quantity we are interested in Frame O' is moving in the +ve direction as seen in O, so u = +4 c/5 The velocity of rocket 2 as seen from O is in the -ve direction, so ux = - 4 c/5 Now, what is the velocity of rocket 2 as seen from frame O', u ’x = ? (intuitively, u ’x must be in the negative direction) 9

Use the LT i. e. the velocity of rocket 2 as seen from rocket 1 (the moving frame, O’) is – 40 c/41, which means that O’ sees rocket 2 moving in the –ve direction (to the left in the picture), as expected. 10

Relativistic Dynamics Still remember conservation of linear momentum? It’s one of the very fundamental law in physics – due to the translational symmetry of space The total linear momentum before and after collision must be the same 11

m 1 u 1 m 2 u 2 m 1 v 1 m 2 v 2 Conservation of momentum means m 1 u 1 +m 2 u 2 = m 1 v 1 +m 2 v 2 Conservation of momentum must also hold true in other inertial reference frames, according to Einstein postulate: m’ 1 u’ 1 +m’ 2 u’ 2 = m’ 1 v’ 1 +m’ 2 v’ 2 (m’ = m in Newton’s mechanics) where the velocities transform according to LT, i. e. u 1 u’ 1 = LT(u 1), v 1 v’ 1 = LT(v 1), etc. 12

Classically, p = mu. In the other frame, p’ = m’u’; the mass m’ (as seen in frame O’) is the same as m (as seen in O frame) – this is according to Newton’s mechanics However, simple consideration will reveal that in order to preserver the consistency between conservation of momentum and the LT, the definition of momentum (as according to Newton’s view) has to be re-defined, such that m’ is not equal to m. That is, the mass of an moving object, m, is different from its value when it’s at rest, m 0 Read lecture notes (or Krane) for a more rigorous illustration why the definition of classical momentum is inconsistent with LT 13

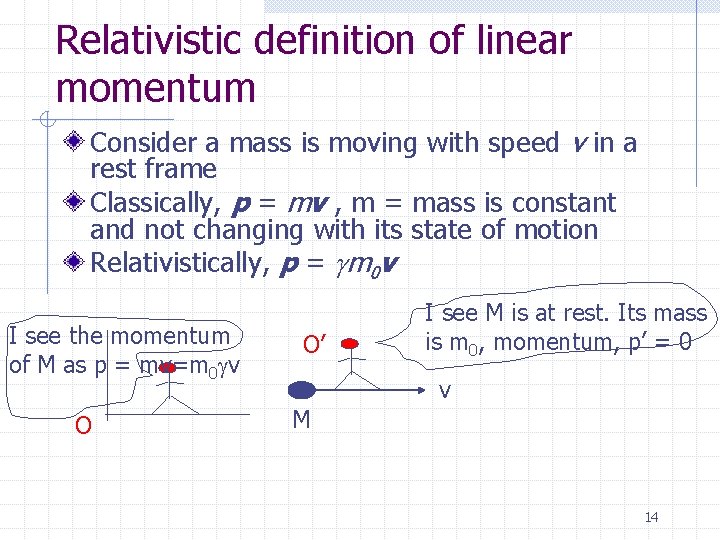
Relativistic definition of linear momentum Consider a mass is moving with speed v in a rest frame Classically, p = mv , m = mass is constant and not changing with its state of motion Relativistically, p = gm 0 v I see the momentum of M as p = mv=m 0 gv O O’ I see M is at rest. Its mass is m 0, momentum, p’ = 0 v M 14

m 0 = rest mass = the mass measured in a frame where the object is at rest. It’s value is a constant m = gm 0 : the mass of a moving object changes as its speed changes g = [1 -(v/c)2]-1/2; where v = | v | 15

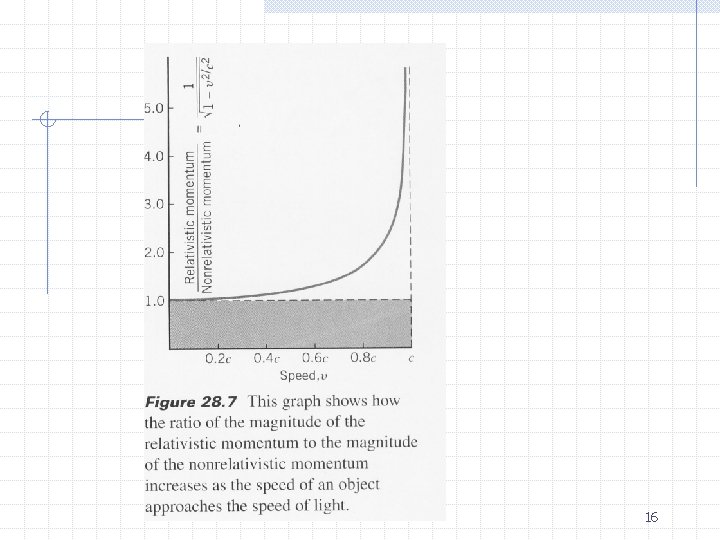
16

Example The rest mass of an electron is m 0 = m 0 9. 11 x 10 -31 kg. If it moves with u = 0. 75 c, what is its relativistic momentum? p = m 0 g u Compare it with that calculated with classical definition. 17

Solution The Lorentz factor is g = [1 -(u/c)2] -1/2 = [1 -(0. 75 c/c)2] -1/2=1. 51 Hence the relativistic momentum is simply p = g x m 0 x 0. 75 c = 1. 51 x 9. 11 x 10 -31 kg x 0. 75 x 3 x 108 m/s = 3. 1 x 10 -22 kg m/s = Ns In comparison, classical momentum gives pclassical = m 0 x 0. 75 c = 2. 5 x 10 -22 Ns – about 34% lesser than the relativistic value 18

For 2 -D case (object moving in the x -y plane) For object moving only in 1 -D (say in the xdirection) with speed vx, its momentum is simply px = m 0 g vx For a mass moving in x-y plane, it has two components of momentum p y = m 0 g vy p = px + py = px i + py j px = m 0 g vx The combined velocity of m is v = vx + vy (vector), with magnitude given by v = [(vx)2 + (vy)2 ]-1/2 The mass changes according to m = m 0 g where g= [1 – (v / c)2] -1/2, depend on the magnitude of the speed the mass is moving (the combined speed)`19

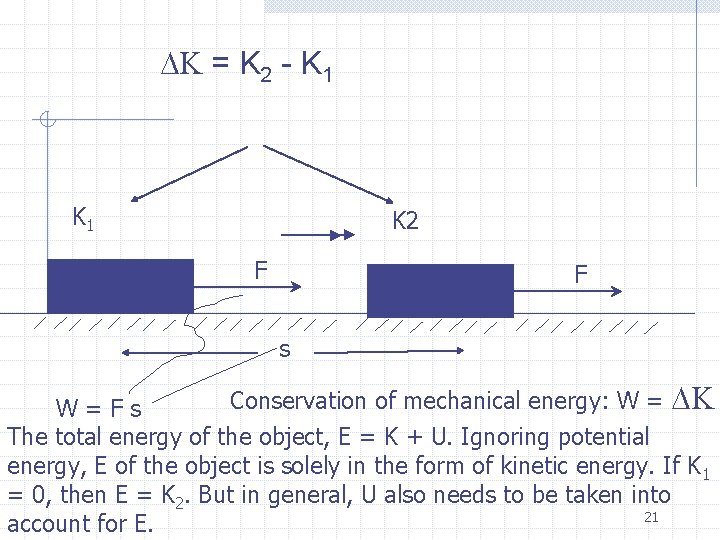
Relativistic Energy Recall the law of conservation of mechanical energy: Work done by external force on an object (W) = the change in kinetic energy of the object, (DK) 20

DK = K 2 - K 1 K 2 F F s Conservation of mechanical energy: W = DK W=Fs The total energy of the object, E = K + U. Ignoring potential energy, E of the object is solely in the form of kinetic energy. If K 1 = 0, then E = K 2. But in general, U also needs to be taken into 21 account for E.

in SR we have redefined the classical mass and momentum to that of relativistic version mclass(cosnt) –> m. SR = m 0 g pclass = mclass u –> p. SR = (m 0 g)u Hence we must also modify the relation btw work and energy so that the law conservation of energy is consistent with SR E. g, in classical mechanics, K = mv 2/2. However, this relationship has to be supplanted by the relativistic version K = mv 2/2 –> K = E – m 0 c 2 = mc 2 - m 0 c 2 We will also see how E = mc 2 comes about in the following 22