TRNG THCS LNG NGC QUYN Gio vin Chu

TRƯỜNG THCS LƯƠNG NGỌC QUYẾN Giáo viên : Chu Thế Hùng Tổ : Khoa học tự nhiên

Kiểm tra Tìm Ư(12) ; Ư(30) ; ƯC (12; 30)? Giải Ư (12) = {1; 2; 3; 4; 6 ; 12} Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30} ƯC (12; 30) = {1; 2; 3 ; 6} 2

Tiết 31: ƯỚC CHUNG LỚN NHẤT

Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất: a) Ví dụ(sgk-54): Ư (12) = {1; 2; 3; 4 ; 6 ; 12} Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30} ƯC (12; 30) = {1; 2; 3 ; 66} Ta nói 6 là ước chung lớn nhất của 12 và 30 b) Kí hiệu : ƯCLN(12; 30) = 6 ƯCLN(a; b): ước chung lớn nhất cuả a và b c) Định nghĩa (sgk-54) Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó. 4

Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất: ƯC (12; 30) = {1; 2; 3; 6} ƯCLN (12 ; 30) = 6 Ư (6) = {1; 2; 3; 6} d) Nhận xét(SGK 54) Tất cả các ước chung của 12 và 30 ( là 1 ; 2 ; 3 ; 6 ) đều là ước của ƯCLNNêu (12 nhận ; 30)xét về mối quan hệ giữa ƯC và ƯCLN ở ví dụ trên

Tiết 31: Ước chung lớn nhất 1. Ước chung lớn nhất: e) Chú ý: Số 1 chỉ có một ước là 1. Do đó, với mọi số tự nhiên a và b, ta có: ƯCLN (a; 1) = 1; ƯCLN (a; b; 1) = 1 VD ƯCLN (5; 1) = 1 ƯCLN (12; 30; 1) = 1 1 6

2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố. a. Ví dụ 2(SGK 55): Tìm ƯCLN(36, 84, 168)

2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố. a. Ví dụ 2(SGK 55): Tìm ƯCLN(36, 84, 168) Giải: 36 = 22. 32 84 = 22. 3. 7 168 = 23. 3. 7 ƯCLN(36, 84, 168) = 22. 3 = 12

2. ? 1(sgk 55) Tìm ước chung lớn nhất bằng cách phân tích các : Tìm ƯCLN(12, 30) số ra thừa số nguyên tố. CÁC C UBƯỚC HỎI TÌMNỘI ƯỚC CHUNG LỚN NHẤT DUNG C U HỎI 6 chính là ước Phân tích số 12 vànhất 30 ra thừa số nguyên tố ? chung lớn 2 tích các thừa số nguyên tố BƯỚC C U 1 1 Phân. 3 số racủa 12 = (2ƯCLN). 3. 5 30 = 2 12 và 30 số nguyên tố chung. Chọn ra các thừa BƯỚC C U 2 2 ; Lậptíchcác cácthừasố sốđã đãchọn, , mỗithừasố sốlấy lấyvới Lập BƯỚC vớimũsốnhỏ mũnhất nhỏ của nhấtnó. của nó. đó là ƯCLN phải tìm C U 3 3 số Tích. =6

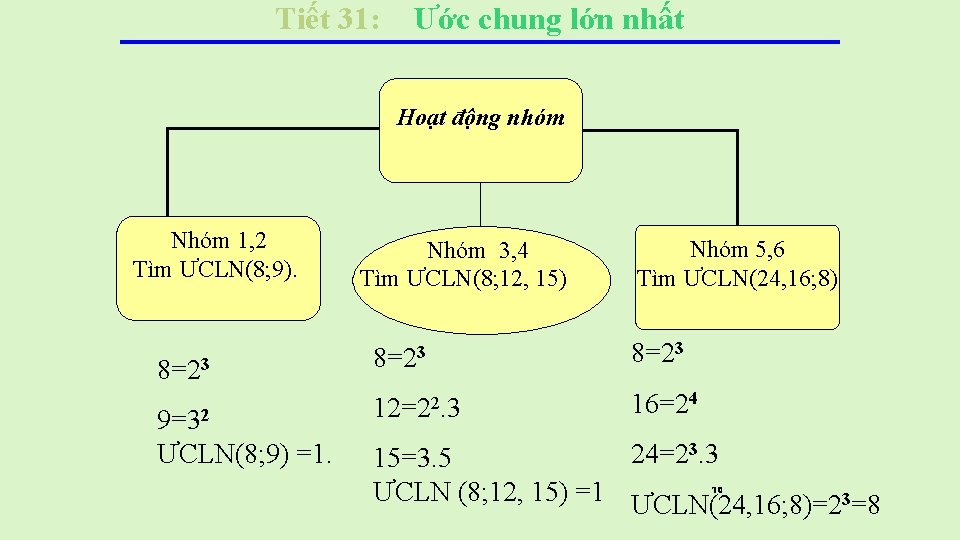
Tiết 31: Ước chung lớn nhất Hoạt động nhóm Nhóm 1, 2 Tìm ƯCLN(8; 9). Nhóm 3, 4 Tìm ƯCLN(8; 12, 15) Nhóm 5, 6 Tìm ƯCLN(24, 16; 8) 8=23 9=32 ƯCLN(8; 9) =1. 12=22. 3 16=24 24=23. 3 15=3. 5 ƯCLN (8; 12, 15) =1 ƯCLN(24, 16; 8)=23=8 10

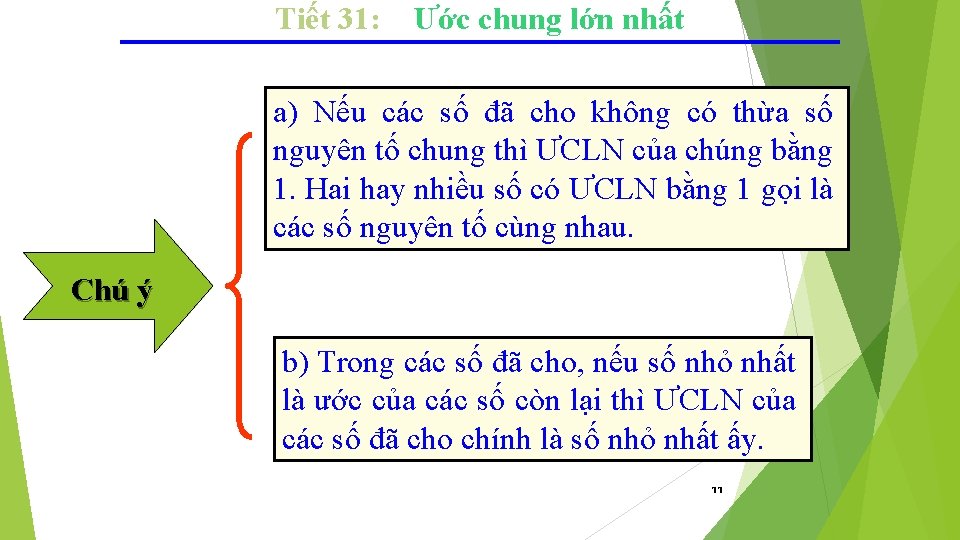
Tiết 31: Ước chung lớn nhất a) Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1. Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau. Chú ý b) Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy. 11

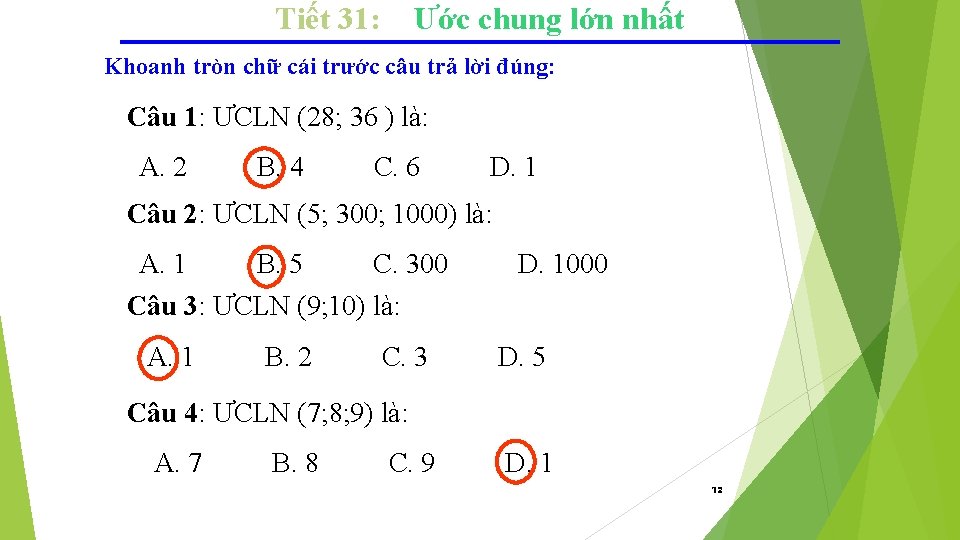
Tiết 31: Ước chung lớn nhất Khoanh tròn chữ cái trước câu trả lời đúng: Câu 1: ƯCLN (28; 36 ) là: A. 2 B. 4 C. 6 D. 1 Câu 2: ƯCLN (5; 300; 1000) là: A. 1 B. 5 C. 300 Câu 3: ƯCLN (9; 10) là: A. 1 B. 2 C. 3 D. 1000 D. 5 Câu 4: ƯCLN (7; 8; 9) là: A. 7 B. 8 C. 9 D. 1 12

TRÒ CHƠI Ô SỐ (Đọc Ô SỐ THEO HÀNG DỌC CÓ Ý NGHĨA GÌ ? ) Câu 1: 4: ƯCLNcủa (11; 2422; 33 ) là: =? Câu và 48 Câu là ướccócủa ? 10 là: Câu 3: 2: Số Số nào tự nhiên haimọi chữsố sốtự là nhiên ước của 2 1 0 1 1 1 4 Câu 1 Đáp án Câu 2 Đáp án Câu 3 Đáp án Câu 4 Đáp án Gợi ý ^_^

DẶN DÒ - Học thuộc thế nào là ƯCLN, cách tìm ƯCLN của các số. - Làm bài 140 ; 142; 143; 145 SGK-56, 176 SBT-28 - Chuẩn bị tiết sau luyện tập. HƯỚNG DẪN VỀ NHÀ Bài 143/SGK: Tìm số tự nhiên a lớn nhất, biết rằng 420 a và 700 a.