Topic 7 Part I Partial Differentiation Part II

Topic 7 Part I Partial Differentiation Part II Marginal Functions Part II Partial Elasticity Part III Total Differentiation Part IV Returns to scale Jacques (4 th Edition): 5. 1 -5. 3 1

Functions of Several Variables n More realistic in economics to assume an economic variable is a function of a number of different factors: Y =f(X, Z) n Demand may depend on the price of the good and the income level of the consumer Qd =f(P, Y) n Output of a firm depends on inputs into the production process like capital and labour Q =f(K, L) 2

Graphically Sketching functions of two variables Y= f (X, Z) n Sketch this function in 3 -dimensional space n or n plot relationship between 2 variables for constant values of the third n 3

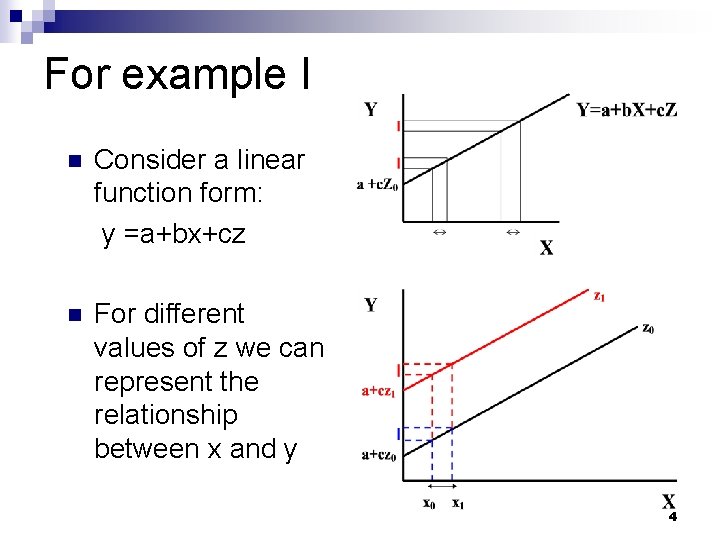
For example I n Consider a linear function form: y =a+bx+cz n For different values of z we can represent the relationship between x and y 4

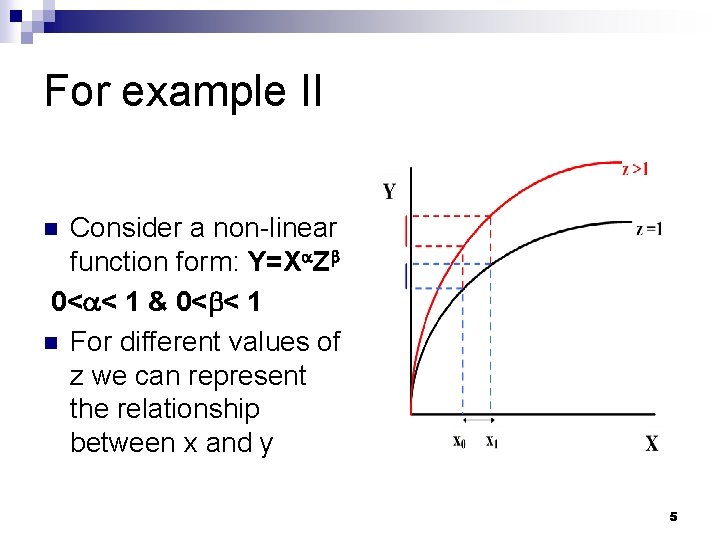
For example II Consider a non-linear function form: Y=X Z 0< < 1 & 0< < 1 n For different values of z we can represent the relationship between x and y n 5

Part I: Partial Differentiation (Differentiating functions of several variables) 6

Consider our function of two variables: Y= f (x, z) = a + bx + cz 7

FOUR Second Order Partial Derivatives 8

Consider our function of two variables: Y= f (X, Z) = X Z First Partial Derivatives Y/ X = f. X = X -1 Z >0 Y/ Z = f. Z = X Z -1 > 0 9

Since Y/ X = f. X = X -1 Z Y/ Z = f. Z = X Z -1 Second own partial 2 Y/ X 2 = f. XX = ( -1) X -2 Z 2 Y/ Z 2 = f. ZZ = ( -1) X Z -2 < 0 Second cross partial 2 Y/ X Z = f. XZ = X -1 Z -1 2 Y/ Z X = f. ZX = X -1 Z -1 > 0 10

Example Jacques Y= f (X, Z) = X 2 +Z 3 f. X = 2 X > 0 Positive relation between x and y f. XX = 2 > 0 but at an increasing rate with x f. XZ = 0, (= fzx) and a constant rate with z impact of change in x on y is bigger at bigger values of x but the same for all values of z f. Z = 3 Z 2 > 0 Positive relation between z and y f. ZZ = 6 Z > 0 but at an increasing rate with z f. ZX = 0 (= fxz) and a constant rate with x impact of change in z on y is bigger at bigger values of z, but the same for all values of x 11

Example Jacques Y= f (X, Z) = X 2 Z f. X = 2 XZ >0 Positive relation between x and y f. XX = 2 Z >0 but at an increasing rate with x f. XZ = 2 X >0 and at an increasing rate with z impact of change in x on y is bigger at bigger values of x and bigger values of z f. Z = X 2 f. ZZ = 0 f. ZX = 2 X >0 Positive relation between z and y but at a constant rate with z >0 and an increasing rate with x impact of change in z on y is the same for all values of z but is bigger 12 at higher values of x

Production function example Y= f(K L) = K 1/3 L 2/3 First partial derivatives of input gives Marginal product of input MPL= Y/ L=YL= ( 2/3 K 1/3 L 2/3 -1) = 2/3 Y/L >0 n An increase in L holding other inputs constant will increase output Y MPK= Y/ K = YK=( 1/3 K 1/3 -1 L 2/3) = 1/3 Y/K > 0 An increase in K holding other inputs constant will increase output Y 13

MPL = Y/ L = ( 2/3 K 1/3 L -1/3) = 2/3 Y/L. MPK = Y/ K = ( 1/3 K-2/3 L 2/3) = 1/3 Y/K. n Second Own derivatives of input gives Marginal Returns of input (or the change in the marginal product of an input with the level of that input) 2 Y/ L 2 = -2/9 K 1/3 L -4/3 < 0 Diminishing marginal returns to L (the change in MPL with L shows that the MPL decreases at higher values of L) 2 Y/ L 2 = -2/9 K-5/3 L 2/3 < 0 Diminishing marginal returns to K (the change in the MPK with K shows that the MPK decreases at higher values of K) 14

Part II: Partial Elasticity 15

e. g. Y= f(K L) = K 1/3 L 2/3 16

P = 10, PS = 12, Y= 1000 Q=192 e. g. demand function Q = f( P, PS, Y) Partial Own-Price Elasticity of Demand QP = Q/ P. P/Q = -2 * (10/192) = - 0. 10 Partial Cross-Price Elasticity of Demand QPS = Q/ PS. PS/Q = +1 * (12/192) = 0. 06 Partial Income Elasticity of Demand QI = Q/ Y. Y/Q = +0. 1 * (1000/192) = 0. 52 17

Part III: Total Differential: Y= f (X) Y= d. Y/d. X. X If X =10 and d. Y/d. X = 2, Y = 2. 10 = 20 Total Differential: Y= f (X, Z) Y= Y/ X. X + Y/ Z. Z or d. Y= Y/ X. d. X + Y/ Z. d. Z 18

Example: Y= f (K, L) = Y = K 1/3 L 2/3 d. Y= Y/ K. d. K + Y/ L. d. L or d. Y= (1/3 K-2/3 L 2/3). d. K + (2/3 K 1/3 L-1/3). d. L Rewriting: d. Y= (1/3 K 1/3 K-1 L 2/3). d. K + (2/3 K 1/3 L 2/3 L-1). d. L or d. Y= 1/3. Y/K. d. K + 2/3. Y/L. d. L To find proportionate change in Y d. Y/ = 1/. d. K/ + 2/. d. L/ Y 3 K 3 L 19

Total Differential: Y= f (X, Z) Y= A f (K, L) = Y = A K L d. Y= Y/ K. d. K + Y/ L. d. L + Y/ A. d. A or d. Y= . AK -1 L d. K + . AK L -1. d. L + K L. d. A d. Y= . Y/K. d. K + . Y/L. d. L + Y/A. d. A Or for proportionate change in Y: d. Y/Y= . d. K/K + . d. L/L + d. A/A Or for proportionate change in A: d. A/A = d. Y/Y–(. d. K/K+. d. L/L) 20

Part IV: Returns to Scale Returns to scale shows the change in Y due to a proportionate change in ALL factors of production. So if Y= f(K, L) Constant Returns to Scale f( K, L ) = f(K, L) = Y Increasing Returns to Scale f( K, L ) > f(K, L) > Y Decreasing Returns to Scale f( K, L ) < f(K, L) < Y 21

Cobb-Douglas Production Function: Y = AK L Quick way to check returns to scale in Cobb. Douglas production function Y = AK L then if + = 1 : CRS if + > 1 : IRS if + < 1 : DRS 22

Example: Y= f(K, L) = A K L Y*= f( K, L) = A ( K) ( L) Y*= A K L = + AK L = + Y + = 1 Constant Returns to Scale + > 1 Increasing Returns to Scale + < 1 Decreasing Returns to Scale 23

Homogeneous of Degree r if: n f( X, Z ) = r f(X, Z) = r Y n Homogenous function if by scaling all variables by , can write Y in terms of r n Note superscripts! n Note then, for cobb-douglas Y = K L , the function is homogenous of degree + 24

Eulers Theorem X f. X + Z f. Z = r f(X, Z) = r. Y E. g. r =1, Constant Returns to Scale If Y= f(K, L) = A K L(1 - ) Does K f. K + L f. L = r. Y = Y ? K ( Y/K) + L((1 - )Y/L) = ? Y + (1 - )Y = Y + Y - Y = Y Thus, Eulers theorem shows (MPk * K ) + (MPL * L) = Y in the case of homogenous production functions of degree 1 25

Example. . If Y = K½ L½ then Y( K, L) = ( K)½ ( L)½ = ½K½ ½L½ = 1 K½ L½ = Y homogenous degree 1. . . constant returns to scale Eulers Theorem: show that K. Y/ K + L. Y/ L = r. Y = Y (r=1 as homog. degree 1) = K. (½. K½ -1. L½) + L. (½. K½. L½ -1) = K(½. Y/K) + L(½. Y/L) = ½. Y + ½. Y = Y 26

Summary: Function of Two Variables Partial Differentiation Production Functions– first derivatives (marginal product of K or L) and second derivatives (returns to K or L) n Partial Elasticity – Demand with respect to own price, price of another good, or income n Total Differentials n Returns to Scale Plenty of Self-Assessment Problems and Tutorial Questions on these things…. n 27