Section 2 1 Linear Equations in One Variable

Section 2. 1 Linear Equations in One Variable

OBJECTIV ES A Determine whether a number is a solution of a given equation.

OBJECTIV ES B Solve linear equations using the properties of equality.

OBJECTIV ES C Solve linear equations in one variable using the six-step procedure(CRAM).

OBJECTIV ES D Solve linear equations involving decimals.

DEFINITION PROPERTIES OF EQUALITIES For real numbers a, b, and 1. a = c. a Reflexive 2. If a = b, then b = a Symmetric 3. If a = b and b = c,

DEFINITION LINEAR EQUATIONS An equation that can be written in the form:

DEFINITION SOLUTIONS OF AN EQUATION Replacements of the variable that make the equation a true statement.

DEFINITION EQUIVALENT EQUATIONS Two equations that have the same solution set.

PROCEDURE Clear fractions/decimals Remove parentheses/simplify Add/Subtract to get variable isolated Multiply/Divide to make coefficient 1

DEFINITION EQUATIONS WITH NO SOLUTIONS AND INFINITELY MANY No SOLUTIONS solutions(contradictions): Infinitely many solutions(identities):

Chapter 2 Linear Equations and Inequalities Section 2. 1 Exercise #5


Chapter 2 Linear Equations and Inequalities Section 2. 1 Exercise #6


Section 2. 2 Formulas, Geometry and Problem Solving

OBJECTIV ES A Solve a formula for a specified variable and then evaluate the answer for given values of the variables.

OBJECTIV ES B Write a formula for a given situation that has been described in words.

OBJECTIV ES C Solve problems about angle measures.

PROCEDURE SOLVE FOR A SPECIFIED VALUE 1. Add or Subtract the same quantity on both sides. 2. Use the distributive property.

Chapter 2 Linear Equations and Inequalities Section 2. 2

Chapter 2 Linear Equations and Inequalities Section 2. 2 Exercise #7

a. Solve for h.

a. Solve for h.


Chapter 2 Linear Equations and Inequalities Section 2. 2 Exercise #9

If thefor perimeter is 100 ft and the a. b. Solve L. length is 20 ft more than the width, what are the dimensions of the rectangle?

a. Solve for L.

b. If the perimeter is 100 ft and the length is 20 ft more than the width, what are the dimensions of the rectangle?


b. If the perimeter is 100 ft and the length is 20 ft more than the width, what are the dimensions of the rectangle?

Chapter 2 Linear Equations and Inequalities Section 2. 2 Exercise #10

These are the alternate exterior angles and they are equal.



Section 2. 3 Problem Solving: Integers and Geometry

OBJECTIV ES A Translate a word expression into a mathematical expression.

OBJECTIV ES B Solve word problems of a general nature.

OBJECTIV ES C Solve word problems about integers.

OBJECTIV ES D Solve word problems about geometric formulas and angles.

PROCEDURE: RSTUV Method for Solving Word Problems Read Select Think Use Verify

Chapter 2 Linear Equations and Inequalities Section 2. 3

Chapter 2 Linear Equations and Inequalities Section 2. 3 Exercise #11

The bill for repairing an appliance totaled $72. 50. If the repair shop charges $35 for the service call, plus $25 for each hour of labor, how many hours labor did the repair take?

Section 2. 4 Problem Solving: Percent, Investment, Motion, and Mixture Problems

OBJECTIV ES A Solve percent problems.

OBJECTIV ES B Solve investment problems.

OBJECTIV ES C Solve uniform motion problems.

OBJECTIV ES D Solve mixture problems.

PROCEDURE: RSTUV Method for Solving Word Problems Read Select Think Use Verify

Chapter 2 Linear Equations and Inequalities Section 2. 4

Chapter 2 Linear Equations and Inequalities Section 2. 4 Exercise #14

An investor bought some municipal bonds yielding 5 percent annually and some certificates of deposit yielding 7 percent. If his total investment amounts to $20, 000 and his annual interest is $1100, how much money is invested in bonds and how much in certificates of deposit?

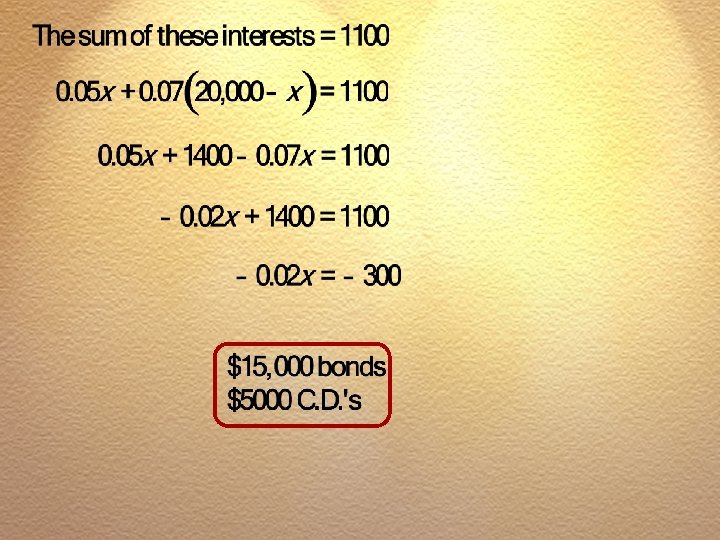

Chapter 2 Linear Equations and Inequalities Section 2. 4 Exercise #15

A freight train leaves a station traveling at 40 mi/hr. Two hours later, a passenger train leaves the same station traveling in the same direction at 60 mi/hr. How far from the station does the passenger train overtake the freight train? Rate Freight Passenger Time Distance

Their distances are equal: Rate Freight Passenger Time Distance

Their distances are equal: The passenger train overtakes the freight train 240 miles from the station. Rate Freight Passenger Time Distance

Section 2. 5 Linear and Compound Inequalities
OBJECTIV ES A Graph linear inequalities.

OBJECTIV ES B Solve and graph linear inequalities.

OBJECTIV ES C Solve and graph compound inequalities.

OBJECTIV ES D Use the inequality symbols to translate sentences into inequalities.

DEFINITION LINEAR INEQUALITIES An inequality that can be written in the form:

DEFINITION UNION OF TWO SETS

DEFINITION INTERSECTION OF TWO SETS

DEFINITION EQUIVALENT STATEMENTS FOR “AND”

Chapter 2 Linear Equations and Inequalities Section 2. 5

Chapter 2 Linear Equations and Inequalities Section 2. 5 Exercise #18

LCD = 24


Chapter 2 Linear Equations and Inequalities Section 2. 5 Exercise #19


Chapter 2 Linear Equations and Inequalities Section 2. 5 Exercise #20
![and ( ] and ( ]](http://slidetodoc.com/presentation_image/eac282a4f767ba7a76234fd6b35ce135/image-78.jpg)
and ( ]

Chapter 2 Linear Equations and Inequalities Section 2. 5 Exercise #21


Section 2. 6 Absolute-Value Equations and Inequality

OBJECTIV ES A Solve absolutevalue equations.
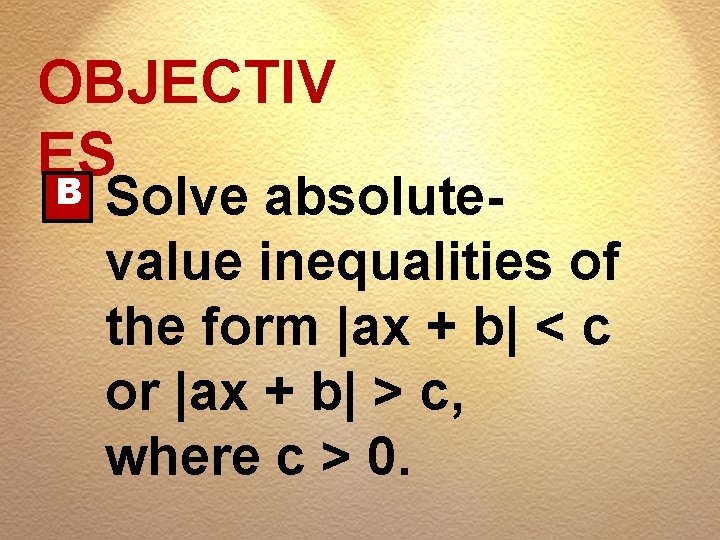
OBJECTIV ES B Solve absolutevalue inequalities of the form |ax + b| < c or |ax + b| > c, where c > 0.

DEFINITION THE SOLUTIONS OF |X| = A (A ≥ 0) If a ≥ 0, the solutions of |x| = a are x = a and x = – a.

STATEMENT TRANSLATION ABSOLUTE VALUE EQUATIONS If |expression| = a, where a≥ 0 or –a expression = a

STATEMENT TRANSLATION ABSOLUTE VALUE EQUATIONS If |expression| = |expression|, expression = –

STATEMENT TRANSLATION |x| = 2: x is exactly 2 units from 0 0 |x| < 2: x is less than 2 units 0 from 0 0 |x| > 2: x is more than 2 units

DEFINITION |x| < a is equivalent to –a < x < a

DEFINITION |x| > a is equivalent to x < –a or x > a

Chapter 2 Linear Equations and Inequalities Section 2. 6

Chapter 2 Linear Equations and Inequalities Section 2. 6 Exercise #22
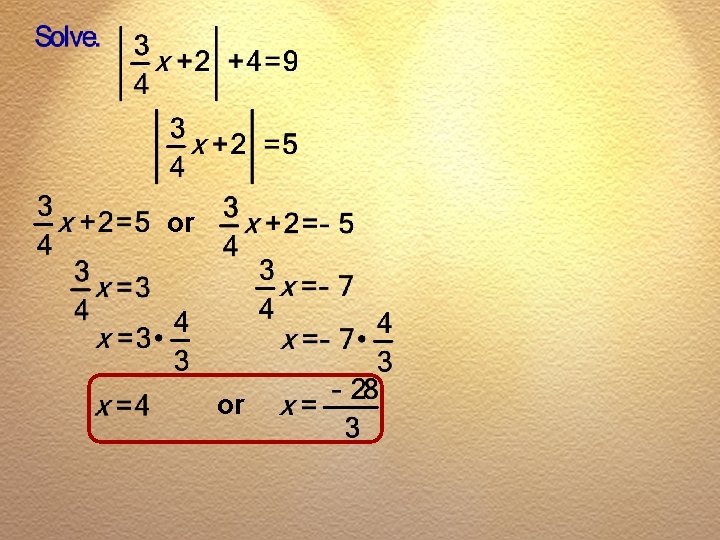
or or

Chapter 2 Linear Equations and Inequalities Section 2. 6 Exercise #23
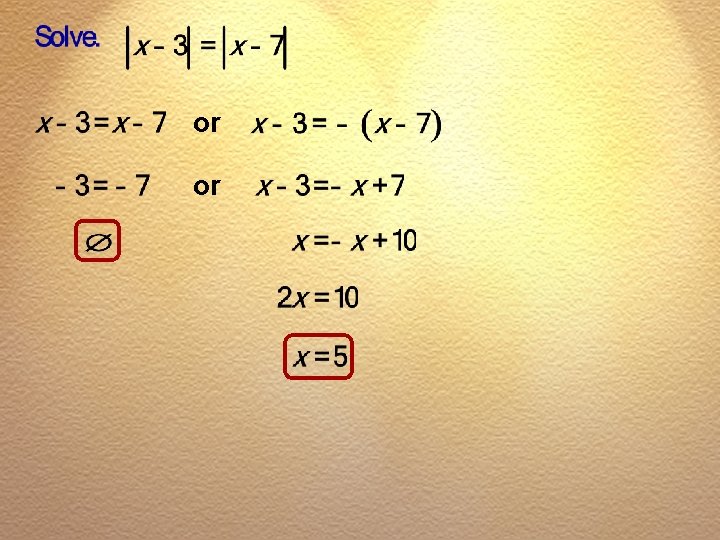
or or

Chapter 2 Linear Equations and Inequalities Section 2. 6 Exercise #24
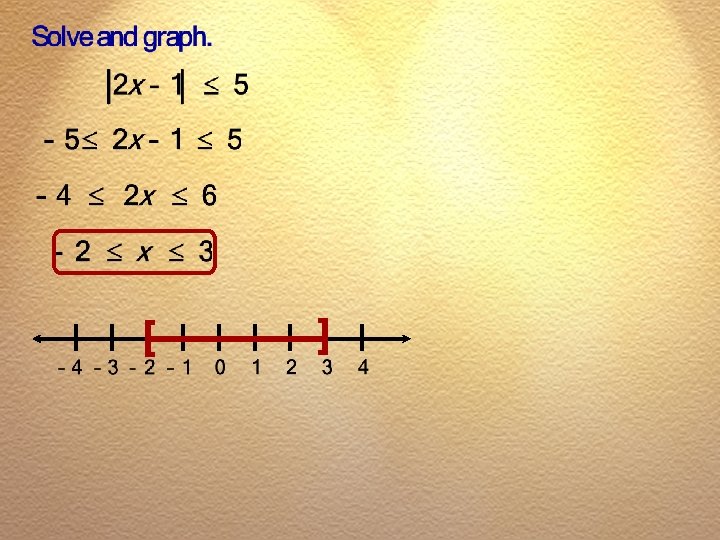

Chapter 2 Linear Equations and Inequalities Section 2. 6 Exercise #25

or or or ) (
- Slides: 98