Three Forms of Quantum Kinetic Equations Evgeni Kolomeitsev

Three Forms of Quantum Kinetic Equations Evgeni Kolomeitsev Matej Bel University, Banska Bystrica Based on: Ivanov, Voskresensky, Phys. Atom. Nucl. 72 (2009) 1168 Kolomeitsev, Voskresensky J Phys. G 40 (2013) 113101 (topical review)

Boltzmann kinetic equation distribution of particles in the phase space binary collisions! drift term Between collisions “particles” move along characteristic determined by an external force Fext collision term: Assumptions: “Stosszahlansatz” (chaos ansatz) -- valid for times larger than a collision time; -- sufficiently long mean free path, but not too long. Conservation: Entropy increase entropy for BKE is local in time and space!

Modifications of the Boltzmann Kinetic Equation: Vlasov equation: plasma Landau collision integral for Coulomb interaction (divergent) Balescu-Lenard (1960) and Silin-Rukhadze(1961) finite collision integral medium polarization Derivation of kinetic equations: Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy Bogoliubov’s principle of weakening of correlations Quantum kinetic equation: Pauli blocking, derivation of QKE

Important assumption behind the above KE: fixed energy-momentum relation In heavy-ion collisions many assumption behind the BKE are not justified At high energies many new particles are produced Resonance dynamics Spectral functions for pions, kaon, nucleons and deltas in medium How to write kinetic equations for resonances?

Pathway to the kinetic equation non-equilibrium field theory formulated on closed real-time contour [Schwinger, Keldysh] non-eq. Green’s functions (only 2 of them are independent) weakening of initial and all short-range correlations Wick theorem Dyson equation: Wigner transformation. Separation of slow and fast variables (Fourier trafo. ) Gradient expansion Poisson brackets: 1 st gradient approximation

Physical notations We introduce quantities which are real and, in the quasi-homogeneous limit, positive, have a straightforward physical interpretation, much like for the Boltzmann equation. Wigner functions 4 -phase-space distribution functions [Ivanov, Knoll Voskresensky, NPA 672 (00) 313; PAN 66(03)1902] spectral density Retarded Green’s function Quasi-particle limit +… weight factor Weight factor is usually dropped It can be hidden in the collision integral phase space distribution as in Boltzmann KE

Kinetic equation in the 1 st gradient approximation Drift operator: for non-relat. part. Collision term: Gain term (production rate): Loss term (absorption rate): The “mass” equation gives a solution for the retarded Green’s function mass function: width: [Ivanov, Knoll Voskresensky, NPA 672 (00) 313; PAN 66(03)1902]

Three forms of the kinetic equation. Kadanoff-Baym equation group velocity Equilibrium relation: Conservation: Noether currents and energy-momentum tensor (if a conservative Phi-derivable scheme is applied) (+ memory terms and derivative terms) Entropy: (Markovian part) H-theorem not proven in general case, only for Because the term does not depend on F explicitly, in the KBE one cannot separate a collision less propagation of a test particle and a collision term. [Ivanov, Knoll Voskresensky, NPA 672 (00) 313; PAN 66(03)1902]

Three forms of the kinetic equation. Botermans-Malfliet Assume small deviation from the local equilibrium replace in the Poisson-bracket term group velocity Conservation: effective current Entropy: (Markovian part) For Markovian part the H-theorem is proven [Ivanov, Knoll Voskresensky, NPA 672 (00) 313; PAN 66(03)1902] Separation of particle drift and collision terms is possible test-particle method [Cassing, Juchem NPA 672; NPA 665, 385; Leupold NPA 672, 475] There exists a well defined hydrodynamic limit [Voskresensky, NPA 849 (11) 120]

Three forms of the kinetic equation. Non-local KE [Ivanov, Voskresensky, Phys. Atom. Nucl 72 (2009)1215] suggested to rewrite KBE as drift term as for BME shifted collision term shifts in time-coordinate and energy-momentum spaces: If we replace CNL with the usual collision integral we obtain BME If we expand the non-local collision term up to 1 st gradients we arrive at KBE Conservation: the same as for KBE (up to 1 st gradients) Entropy: (Markovian part)

Characteristic times KBE: relaxation time or an average time between collisions BME: time delay/advance of the scattered wave in the resonance zone NLE: BME with forward-time in KE can be positive (delay) near resonance and negative (advance) far from resonance

Spectral density normalizations density of state Ergodicity Noether particle density. Conserved by KBE exactly and by BME approximately Current conserved by BME exactly [Delano, PRA 1(1970) 1175] unstable particle gas Current conserved only approximately Wigner time [Weinhold, Friman, Nörenberg PLB 433 (98) 236]

Examples of solutions of kinetic equations Consider behavior of a dilute admixture of uniformly distributed light resonances in an equilibrium medium consisting of heavy-particles. Thereby, we assume that SR is determined by distribution of heavy particles, Light resonance production by heavyparticles is determined by the equilibrium production rate. collision integral: KBE: BME: NLE: different answers!! where a is the solution of equation Three solutions coincide only for. However this condition may hold only in very specific situations. For Wigner resonances it holds only for

Resonance life time [Leupold, NPA 695 (2001 377] Spatially uniform dilute gas of non-interacting resonances produced at t<0 and placed in the vacuum at t=0. Production of new resonances ceases for t>0 : From the BME Leupold got the solution: On the contrary, from the KBE one finds: NLE However, the BME does not hold for Gin=0, since its derivation is based on the equation Gin=G f !

Problems

Time shifts in the collision integral collision term last collision happened in the remote past resonances “feel the future collision” Advances and delays in time are quite common in classical and quantum mechanics Scattering of particles on hard spheres

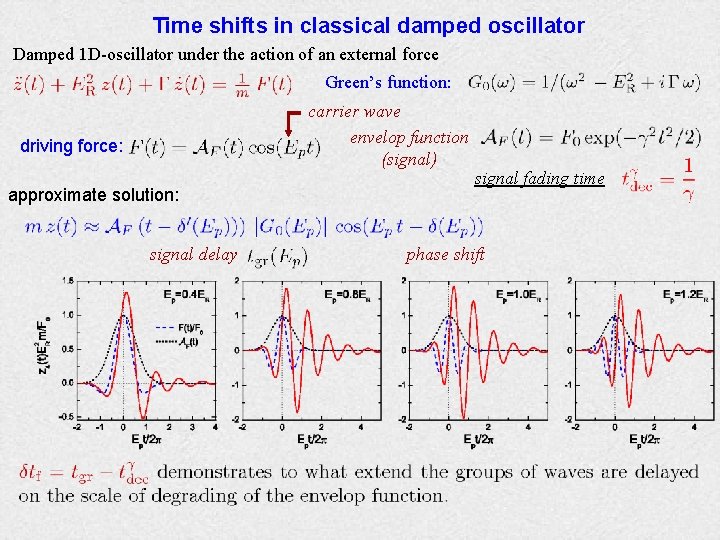
Time shifts in classical damped oscillator Damped 1 D-oscillator under the action of an external force Green’s function: carrier wave envelop function (signal) driving force: approximate solution: signal delay signal fading time phase shift

Quantum scattering in 3 D partial wave Wigner time delay: analogue of the signal delay quasi-particle and Noether currents different waves Difference of flight times w. and wo. potential

Conclusion KBE 1 st gradient expansion NLE KBE=NLE=BME+ phase-space shifts in the collision term BME Three forms of kinetic equations have different relaxation times! On large time scale >>1/G all froms are equivalent. Resonance life time does not follow from BME since BME cannot be used for studying resonance decays. One cannot put Gin=0 in BME Time shift in the collision integral for NLE can be >0 (delay) or <0 (advance) Time delays/advances are quite common in classical and quantum mechanics, QFT and quantum kinetics. see [J Phys. G 40 (2013) 113101] for examples