Linear Functions Slope Different Forms of Linear Equations

Linear Functions Slope Different Forms of Linear Equations Graphing Linear Inequalities and Systems Misc. Linear Functions $100 $200 $200 $100 $200 Parallel & Perpendicular Lines $300 $300 $400 $400 $500 $500

$100 Question Linear Functions Explain how you know if a graph represents a linear function

$100 Answer Linear Functions A graph represents a linear function if it is a straight line **vertical lines are linear but not functions (fails vertical line test. )

$200 Question Linear Functions Which table(s) are linear? Explain how you know. A. B.

$200 Answer Linear Functions B. ) x and y are both going up with constant rates * same rate of change * Rate of change = change of y change of x x is not a constant change in table A

$300 Question Linear Functions Make a table and graph for y = -x + 3 Is this equation linear? Explain.

$300 Answer Linear Functions Graph has a negative slope—straight line It is a linear function because table has a constant rate of change and graph is a straight line

$400 Question Linear Functions Let y = 2 x + 9. If the value of x increases by 6, which of the following best describes the change in the value of y. a. ) decreases by 6 b. ) increases by 6 c. ) increases by 12 d. ) increases by 21

$400 Answer Linear Functions As x goes up by 6 The value of y. c. ) increases by 12

$500 Question Linear Functions Which of the following equations is not linear? Explain or show you know. A) y = 2 x 2 – 7 B) -6 = y C) 4 x – 2 y = 10 D) y = 3 x + 1

$500 Answer Linear Functions A) y = 2 x 2 – 7 not linear--exponent B) -6 = y horizontal—straight line C) 4 x – 2 y = 10 standard form x and y-int. --line D) y = 3 x + 1 slope-int. —always form a line

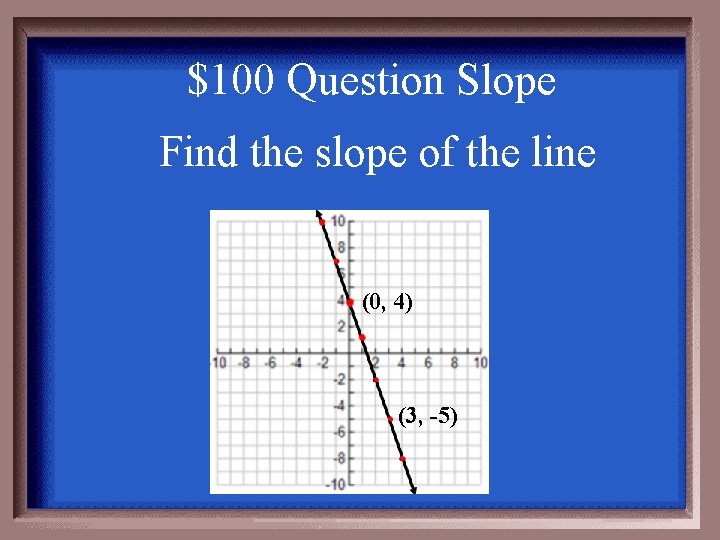
$100 Question Slope Find the slope of the line (0, 4) (3, -5)

$100 Answer Slope Rise Run m = -3

$200 Question Slope Write the equation of the line that passes through each pair of points in slopeintercept form (-1, 5) and (2, -4)

$200 Answer Slope 1. ) Find Slope m = -3 2. ) Choose a point (-1, 5) Use point-slope form then solve for y Y = -3 x + 2

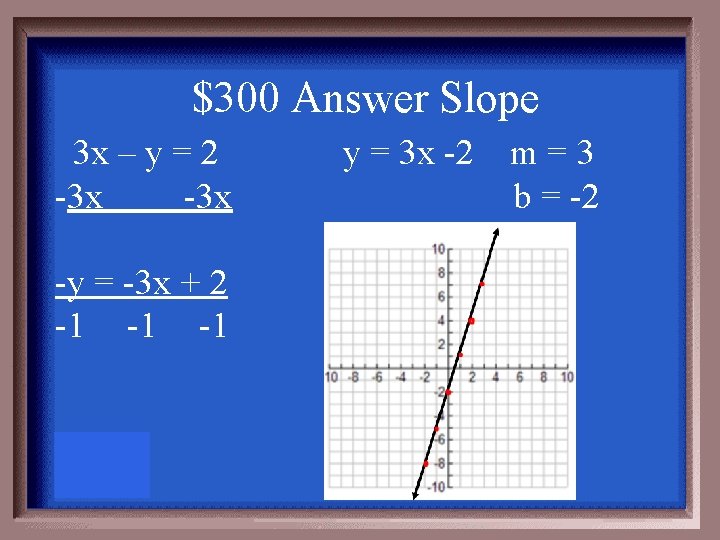
$300 Question Slope Put the following equation into slopeintercept form. Identify the slope and yintercept. Then use the slope and y-int. to graph the line. 3 x – y = 2

$300 Answer Slope 3 x – y = 2 -3 x -y = -3 x + 2 -1 -1 -1 y = 3 x -2 m=3 b = -2

$400 Question Slope Laurel graphed the equation y = -2 x + 5. Katelyn then graphed an equation that was a line that was not as steep as Laurel’s. Which equation could have been the one Katelyn graphed? a. ) y = -3 x + 5 b. ) y = 1/2 x + 6 c. ) y = 4 x – 2 d. ) y = -2 x + 3

$400 Answer Slope B. ) y = 1/2 x + 6 is not as steep. Fractions (between -1 and 1: non-improper) are less steep than any integer— even if it’s negative.

$500 Question Slope The cost of hiring Zach as a painter is given by the linear equation C = 10 t + 100, where t is the number of hours Zach works. Identify the slope and y-int. What does the slope of the line represent? What does the y-intercept represent?

$500 Answer Slope m = 10 The slope means Zach earns $10 per hour. b = 100 The y-intercept represents base charge of hiring Zach (when he’s worked 0 hours, we’d still have to pay him $100

$100 Question Parallel & Perpendicular Lines What are two different ways that lines can be perpendicular?

$100 Answer Parallel & Perpendicular Lines Vertical lines are perpendicular to a horizontal lines. Ex. x = 3 and y = -2 When the product of slopes = -1 (or are negative reciprocals of each other) Ex. 4 and -1/4

$200 Question Parallel & Perpendicular Lines A line has the equation x + 2 y = 5 What is the slope of a line parallel to this line? a. ) – 2 b. ) - ½ c. ) ½ d. ) 2

$200 Answer Parallel & Perpendicular Lines A line has the equation x + 2 y = 5 1. Put line in slope-int. form y = -1 x + 5 2 2 2. Parallel -- same slope -- b. ) - ½

$300 Question Parallel & Perpendicular Lines

$300 Answer Parallel & Perpendicular Lines A. 1 and -1 are “opposite reciprocals”

$400 Question Parallel & Perpendicular Lines

$400 Answer Parallel & Perpendicular Lines Line AB has a slope of 1 and Line BC has a slope of -3/2 and Line AC has a slope of 0. None of the slopes will have a product of -1 (are negative reciprocals) so D is the answer

$500 Question Parallel & Perpendicular Lines Write an equation that is perpendicular to the given line below that passes through the point (- 6, 2)

$500 Answer Parallel & Perpendicular Lines 1. Slope will be -3 (opp. reciprocal) 2. Use point-slope form y- 2 = -3(x – (-6)) Distributive Prop. y = -3 x -16

$100 Question Different Forms of Linear Equations Find and use the x and y intercepts to graph the line. -x + 3 y = 6

$100 Answer Different Forms of Linear Equations -x + 3 y = 6 0 + 3 y = 6 -x + 3(0) = 6 y-int. = 2 -x = 6 (0, 2) x-int. = -6 (-6, 0) (0, 2) (-6, 0)

$200 Question Different Forms of Linear Equations Find and use the x and y intercepts to graph the line. -2 x = 12 + 4 y

$200 Answer Different Forms of Linear Equations -2 x = 12 + 4 y -4 y from both sides -2 x - 4 y = 12 Now in standard form x-int. = (-6, 0) y-int. = (0, -3) (-6, 0) (0, -3)

$300 Question Different Forms of Linear Equations What is the x-intercept of the linear function f(x) = -3 x + 6? Note: f(x) is another way to write ‘y’ a. ) -2 b. ) 2 c. ) 3 d. ) 6

$300 Answer Different Forms of Linear Equations f(x) = -3 x + 6 Think: y = -3 x + 6 add 3 x to both sides –standard form y + 3 x = 6 0 + 3 x = 6 x-int. = 2 (b)

$400 Question Different Forms of Linear Equations A line has a slope of 2/3 and passes through the point (-3, 4). What is the equation of the line in point-slope form? What is the equation of the line in slope-intercept form?

$400 Answer Different Forms of Linear Equations Point-slope form y- 4 = 2/3[x – (-3)] y – 4 = 2/3(x + 3) Slope-Intercept Form y = 2/3 x + 6

$500 Question Different Forms of Linear Equations Is every linear relationship a direct variation? Is every direct variation a linear relationship? Explain.

$500 Answer Different Forms of Linear Equations Every linear relationship is not a direct variation —only if the y-int. is 0. However, every direct variation is linear because it has a constant rate of change. Direct Variation: y = 3 x (also linear) Not a direct variation y = 3 x +5 (is linear)

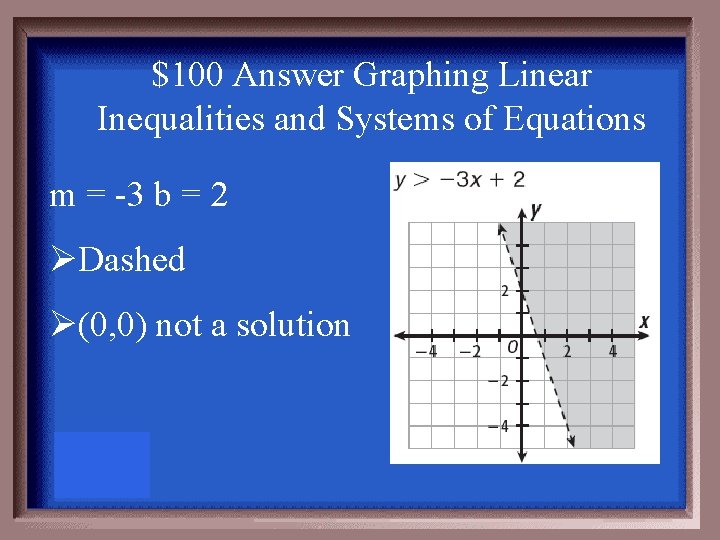
$100 Question Graphing Linear Inequalities and Systems of Equations Graph each inequality y > -3 x + 2

$100 Answer Graphing Linear Inequalities and Systems of Equations m = -3 b = 2 ØDashed Ø(0, 0) not a solution

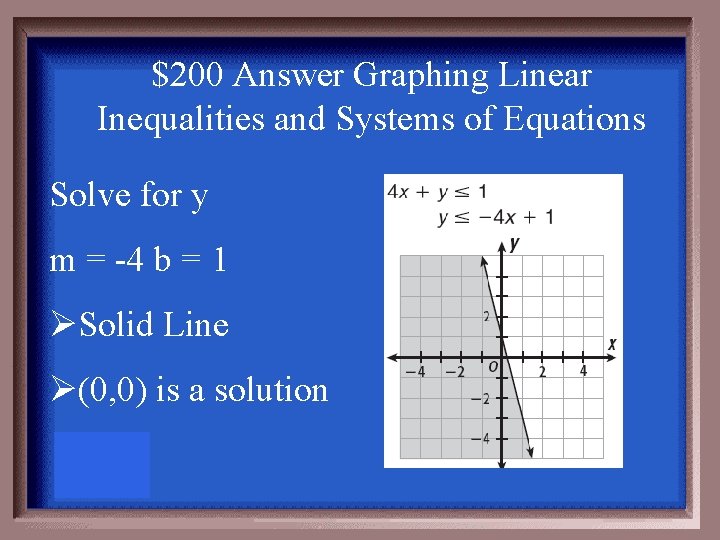
$200 Question Graphing Linear Inequalities and Systems of Equations Graph each inequality 4 x + y ≤ 1

$200 Answer Graphing Linear Inequalities and Systems of Equations Solve for y m = -4 b = 1 ØSolid Line Ø(0, 0) is a solution

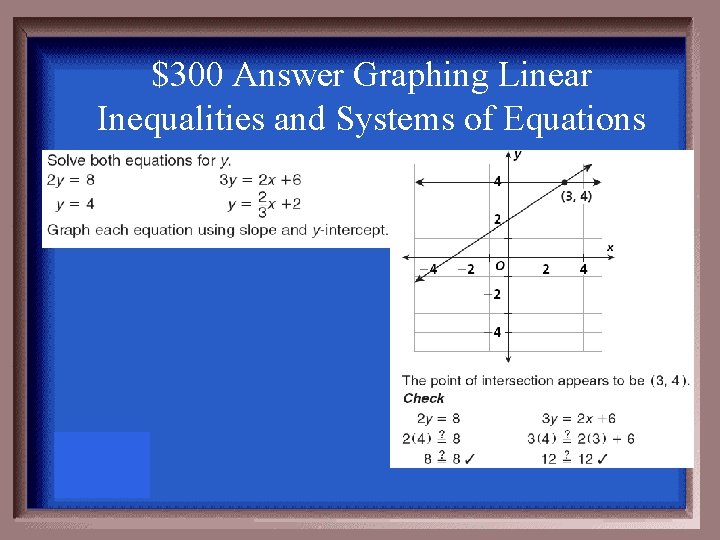
$300 Question Graphing Linear Inequalities and Systems of Equations Solve the system by graphing 2 y = 8 3 y = 2 x + 6

$300 Answer Graphing Linear Inequalities and Systems of Equations

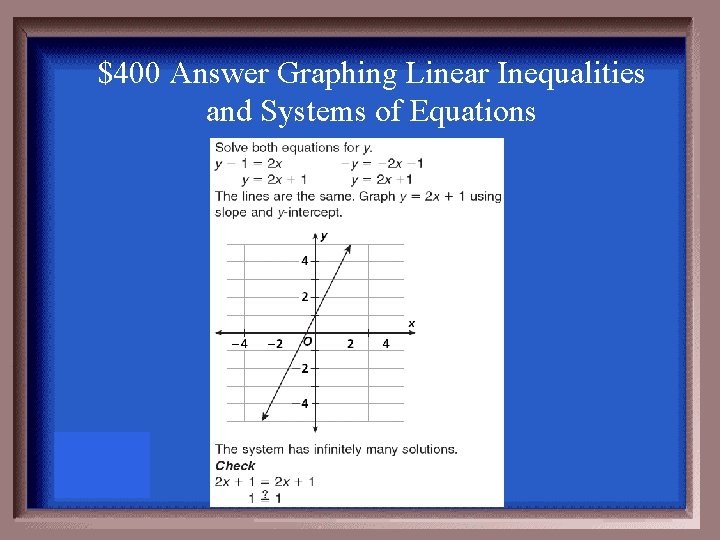
$400 Question Graphing Linear Inequalities and Systems of Equations Solve the system by graphing y – 1 = 2 x -y = -2 x -1

$400 Answer Graphing Linear Inequalities and Systems of Equations

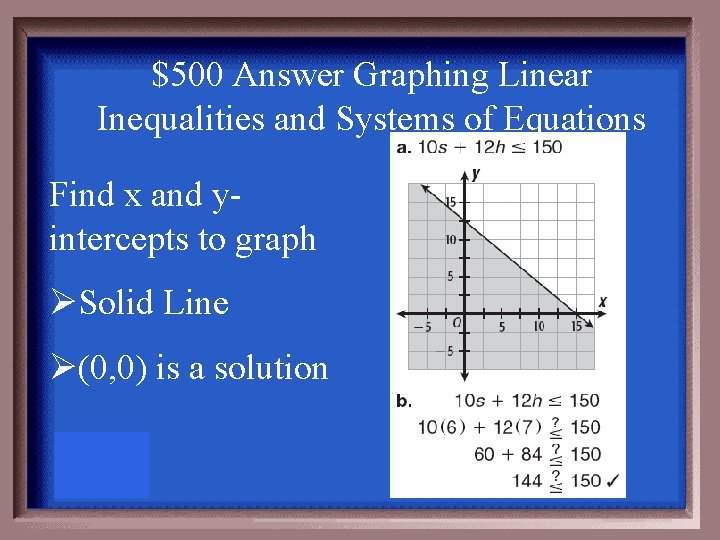
$500 Question Graphing Linear Inequalities and Systems of Equations

$500 Answer Graphing Linear Inequalities and Systems of Equations Find x and yintercepts to graph ØSolid Line Ø(0, 0) is a solution

$100 Question Miscellaneous The table shows an employee’s pay per hour. Determine if there is a direction variation between the pay and number of hours worked. If so, find the equation of direct variation

$100 Answer Miscellaneous You can use the ratio to check. 17/2 = 8. 5 and 34/4 = 8. 5 ratios are = (proportional) so it’s a direct variation The equation would be y = 8. 5 x

$200 Question Miscellaneous Solve the system by substitution x = 2 y + 6 y = -3 x + 4

$200 Answer Miscellaneous Could have also substituted top equation into the bottom.

$300 Question Miscellaneous Solve the system of equations x–y=4 x – 2 y = 10

$300 Answer Miscellaneous Could have used other ways to eliminate or you could have used the substitution or graphing methods Remember to check your answer by substituting solution into each original equation.

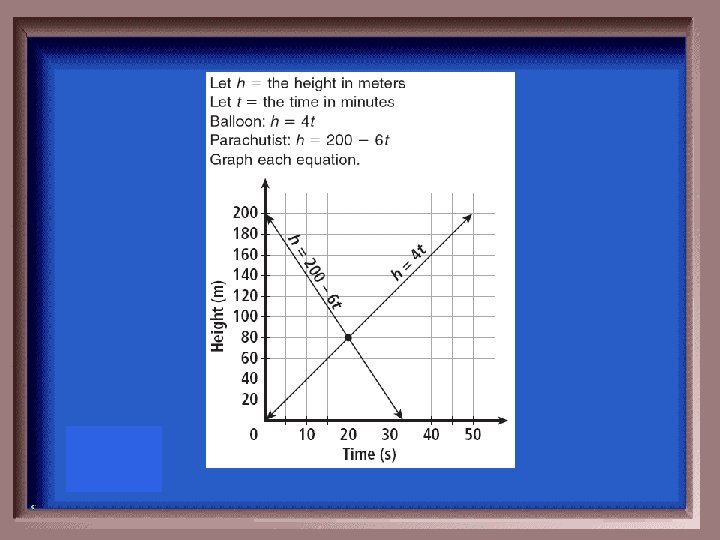
$400 Question Miscellaneous

$400 Answer Miscellaneous

$500 Question Miscellaneous Solve the system of equations by elimination

$500 Answer Miscellaneous Could have also eliminated the y’s Remember to check your answer by substituting solution into each original equation.