WorkEnergy Theorem and Conservation of Mechanical Energy From

Work-Energy Theorem and Conservation of Mechanical Energy From: http: //www. myteacherpages. com/webpages/MNeipp/files/work%20&%2 0 energy. ppt.

THE PRINCIPLE OF CONSERVATION OF ENERGY Energy can neither be created nor destroyed, but can only be converted from one form to another. * Disclaimer: This powerpoint presentation is a compilation of various works.

Mechanical Energy n Objects have mechanical energy if they are in motion and/or if they are at some position relative to a zero potential energy position

Total Mechanical Energy *Total Mechanical Energy: The sum of kinetic energy & all forms of potential energy 1. Kinetic Energy (Energy of motion) KE = ½ mv 2 2. Potential Energy (Stored energy of position) a. Gravitational PEg = mgh b. Elastic PEelastic = ½ kx 2

Mechanical Energy CONSERVATION OF MECHANICAL ENERGY: * In the absence of friction, mechanical energy is conserved, so the amount of mechanical energy remains constant MEi = MEf Initial mechanical energy = final mechanical energy (in the absence of friction) PEi + KEi = PEf + KEf mghi + ½ mvi 2 = mghf + ½ mvf 2

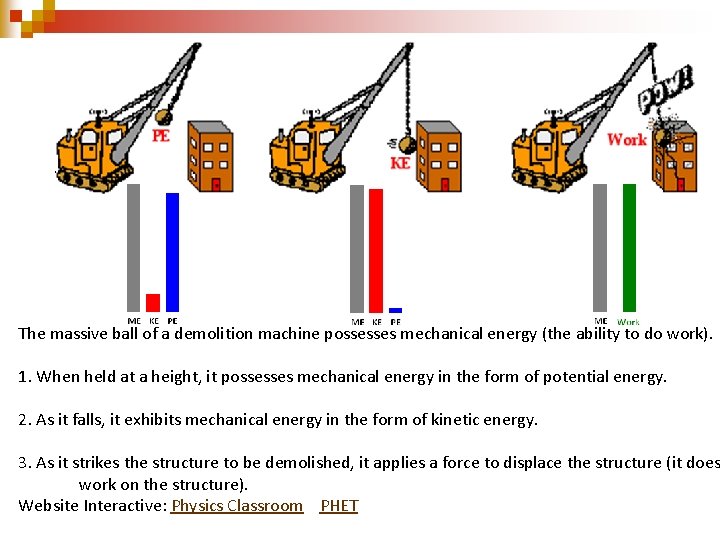
Mechanical Energy Ability to do Work n An object that possesses mechanical energy is able to do work Its mechanical energy enables that object to apply a force to another object in order to cause it to be displaced n Classic Example Massive wrecking ball of a demolition machine n

Mechanical Energy v Work is a force acting on an object to cause a displacement v In the process of doing work the object which is doing the work exchanges energy with the object upon which the work is done v When work is done up the object that object gains energy

Mechanical Energy n A weightlifter applies a force to cause a barbell to be displaced ¨ Barbell now possesses mechanical energy- all in the form of potential energy ** The energy acquired by the objects upon which work is done is known as mechanical energy

Mechanical Energy is the ability to do work… Massive wrecking ball of a demolition machine The wrecking ball is a massive object which is swung backwards to a high position and allowed to swing forward into a building structure or other object in order to demolish it Upon hitting the structure, the wrecking ball applies a force to it in order to cause the wall of the structure to be displaced Mechanical energy = ability to do work

The massive ball of a demolition machine possesses mechanical energy (the ability to do work). 1. When held at a height, it possesses mechanical energy in the form of potential energy. 2. As it falls, it exhibits mechanical energy in the form of kinetic energy. 3. As it strikes the structure to be demolished, it applies a force to displace the structure (it does work on the structure). Website Interactive: Physics Classroom PHET

Conservation of Energy Problem Starting from rest, a child zooms down a frictionless slide from an initial height of 3 m. What is her speed at the bottom of the slide? (Assume she has a mass of 25 kg)

Conservation of Energy Problem hi = 3 m hf = 0 m • • • vi = 0 m/s Slide is frictionless Mechanical energy is conserved Kinetic energy & potential energy = only forms of energy present • • m = 25 kg vf = ? KE = ½ mv 2 PEg = mgh Final gravitational potential energy = zero (Bottom of the slide) PEgf = 0 Initial gravitational potential energy Top of the slide PEgi = mghi (25 kg)(9. 8 m/s 2)(3 m) = 736 J

Conservation of Energy Problem hi = 3 m hf = 0 m • KEi = 0 Final Kinetic Energy • • vi = 0 m/s Initial Kinetic Energy = 0, because child starts at rest • • m = 25 kg vf = ? KEf = ½ mv 2 ½ (25 kg)v 2 f MEi = MEf PEi + KEi = PEf + Kef 736 J + 0 J = 0 J + (1/2)(25 kg)(v 2 f) vf = 7. 67 m/s

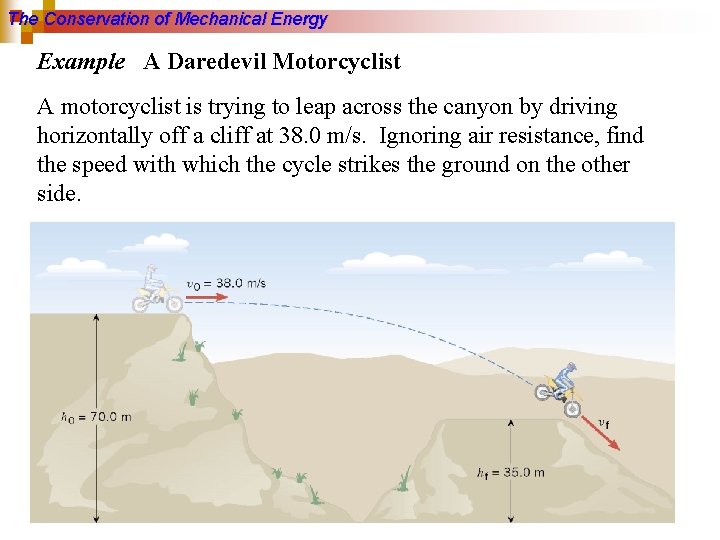
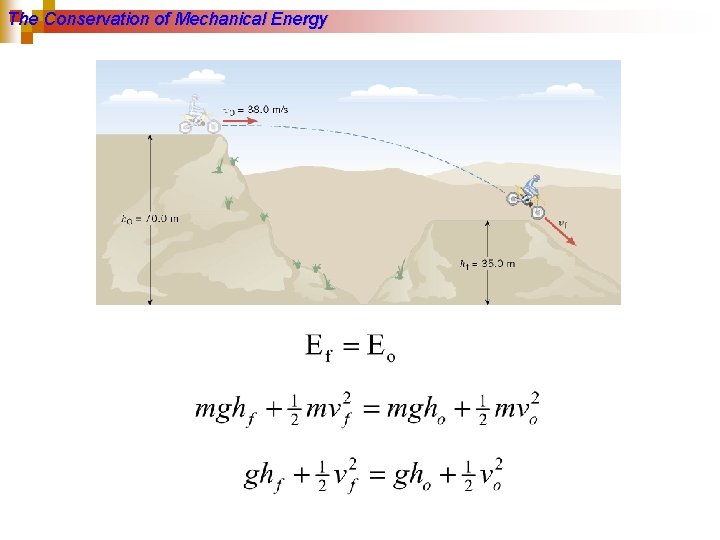
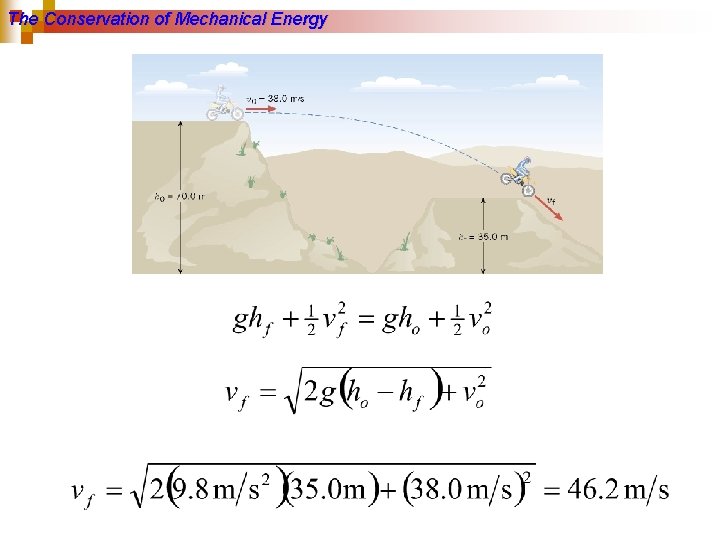
The Conservation of Mechanical Energy Example A Daredevil Motorcyclist A motorcyclist is trying to leap across the canyon by driving horizontally off a cliff at 38. 0 m/s. Ignoring air resistance, find the speed with which the cycle strikes the ground on the other side.

The Conservation of Mechanical Energy

The Conservation of Mechanical Energy

Work-Kinetic Energy Theorem Work-kinetic Energy Theorem: • Net work done on a particle equals the change in its kinetic energy (KE) W = ΔKE

Linking Work to Mechanical Energy WORK is a force acting upon an object to cause a displacement n When work is done upon an object, that object gains energy n Energy acquired by the objects upon which work is done is known as MECHANICAL ENERGY n

Work- Energy Theorem External Forces: Applied force, normal force, tension force, friction force and air resistance force Internal Forces: Gravity forces, spring forces, electrical forces and magnetic forces

PROBLEM n What is the soccer ball’s speed immediately after being kicked? Its mass is 0. 42 kg.

PROBLEM n What is the soccer ball’s speed immediately after being kicked? Its mass is 0. 42 kg. vi=0 W = F ∙ Δx W = (240 N) (0. 20 m) = 48 J W = ΔKE = 48 J KE = ½ mvf 2 - ½ mvi 2 = 48 J v 2 = 2(48 J)/0. 42 kg v = 15 m/s

Work-Kinetic Energy Theorem On a frozen pond, a person kicks a 10 kg sled, giving it an initial speed of 2. 2 m/s. How far does the sled move if the coefficient of kinetic friction between the sled and the ice is 0. 10? m = 10 kg vi = 2. 2 m/s vf = 0 m/s μk = 0. 10 d=?

Wnet = Δ KE = ½ mv 2 f – ½ mv 2 i Δ KE = 0 * Net work done is the final KE of the sled minus the initial KE. First find the work done by friction. Wfric = μk*mg*d*cosθ Wfric = (0. 10)(10 kg)(9. 81 m/s 2)(-1) * d = -9. 8 d * The force of kinetic friction is in the direction opposite of d θ = 180°. Cos(180)= -1 * Next find the KE of the sled in J. Sled comes to rest So, final KE = 0. All you have left is initial KE Δ KE= -1/2 mv 2 i 2

Work-Kinetic Energy Theorem Use the work-kinetic energy theorem, and solve for d Wnet = ΔKE -9. 8 N * d= -24 J d = 2. 4 m

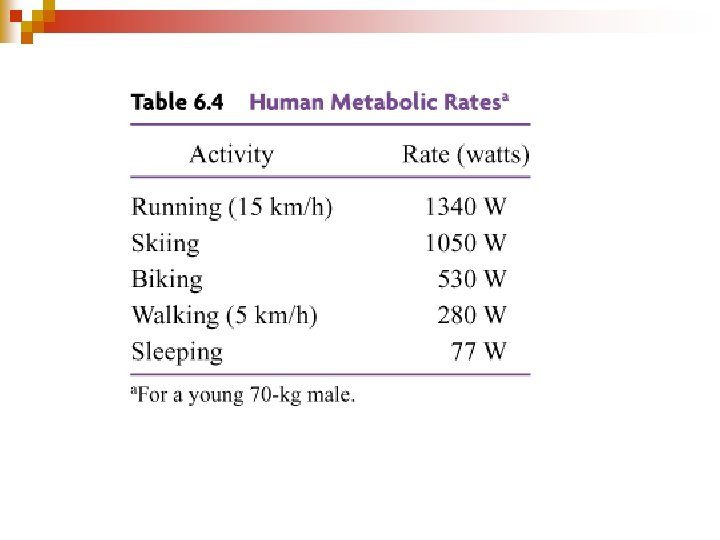
POWER SI Unit for Power: Watt (W) Defined as 1 joule per second (J/s) Horsepower = Another unit of power 1 hp = 746 watts

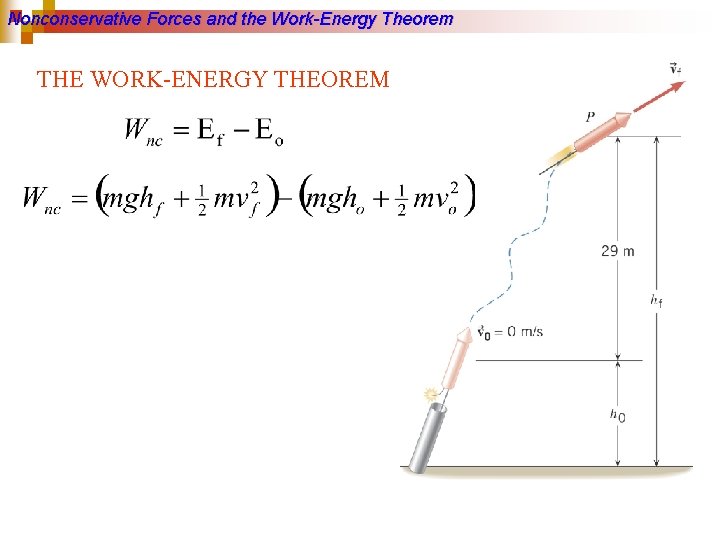
Nonconservative Forces and the Work-Energy Theorem THE WORK-ENERGY THEOREM

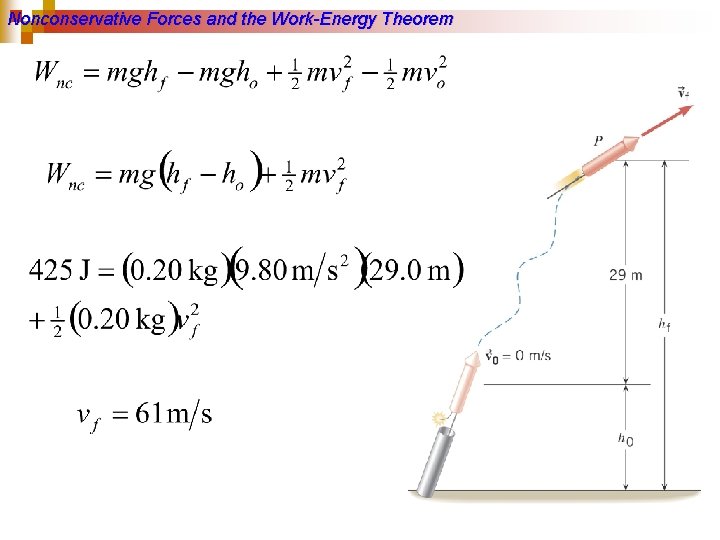
Nonconservative Forces and the Work-Energy Theorem Example Fireworks Assuming that the nonconservative force generated by the burning propellant does 425 J of work, what is the final speed of the rocket. Ignore air resistance. The mass of the rocket is 0. 2 kg.

Nonconservative Forces and the Work-Energy Theorem

POWER: * A quantity that measures the rate at which work is done or energy is transformed * Power = work / time interval P = W/Δt W = Fd P = Fd/Δt * Power = Force x speed P = Fv v = d/Δt

POWER SI Unit for Power: Watt (W) Defined as 1 joule per second (J/s) Horsepower = Another unit of power 1 hp = 746 watts

POWER PROBLEM A 193 kg curtain needs to be raised 7. 5 m, in as close to 5 s as possible. The power ratings for three motors are listed as 1 k. W, 3. 5 k. W, and 5. 5 k. W. What motor is best for the job?

POWER PROBLEM m = 193 kg Δt = 5 s d =7. 5 m P=? P = W/Δt = Fd/Δt = mgd/Δt = (193 kg)(9. 8 m/s 2)(7. 5 m)/5 s = 280 W 2. 8 k. W ** Best motor to use = 3. 5 k. W motor. The 1 k. W motor will not lift the curtain fast enough, and the 5. 5 k. W motor will lift the curtain too fast

Question A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3. 0 kg and the height of the seat top is 0. 45 meters, then what is the potential energy of the loaded cart at the height of the seat-top? PE = m*g*h PE = (3 kg ) * (9. 8 m/s/s) * (0. 45 m) PE = 13. 2 J

Question If a force of 14. 7 N is used to drag the loaded cart (from previous question) along the incline for a distance of 0. 90 meters, then how much work is done on the loaded cart? W = F * d * cos Theta W = 14. 7 N * 0. 9 m * cos (0 degrees) W = 13. 2 J (Note: The angle between F and d is 0 degrees because the F and d are in the same direction)