Systems of Linear Equations in Vector Form Prepared

Systems of Linear Equations in Vector Form Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Any system of linear equations can be put into matrix form: Or vector form: The vectors in the vector form of the equation are the columns of the matrix A in the matrix format. Here a few examples: This is a HOMOGENEOUS system because the right side is all 0. This is a NON-HOMOGENEOUS system because the right side is not all 0. Here we have fewer equations than unknowns. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Here are the vectors for this system. The vectors in the vector form of the equation are the columns of the matrix A in the matrix format. Row reduction yields: Here is the corresponding solution. The lack of a pivot in column three indicates a free variable, and an infinite # of solutions Rename x 3, call it ‘t’, and we get a vector solution (this is a 1 -dimensional subset of ℝ 3): Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

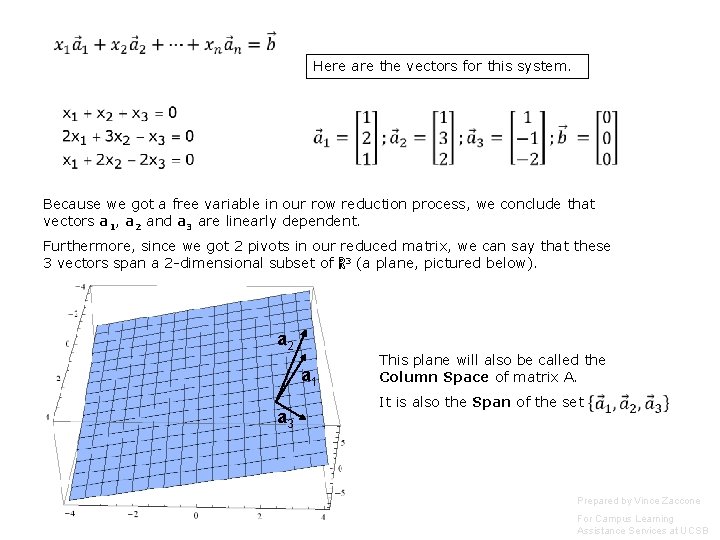
Here are the vectors for this system. Because we got a free variable in our row reduction process, we conclude that vectors a 1, a 2 and a 3 are linearly dependent. Furthermore, since we got 2 pivots in our reduced matrix, we can say that these 3 vectors span a 2 -dimensional subset of ℝ 3 (a plane, pictured below). a 2 a 1 a 3 This plane will also be called the Column Space of matrix A. It is also the Span of the set Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Here are the vectors for this system. Because we got a free variable in our row reduction process, we have infinitely many solutions to the system. The set of all solutions form a 1 -dimensional subspace of ℝ 3. Since this system is homogeneous, we call this solution set the Null Space of matrix A. The solution was written as a vector. The Null Space consists of all multiples of this vector. Geometrically, this space is a line in ℝ 3, pictured below. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

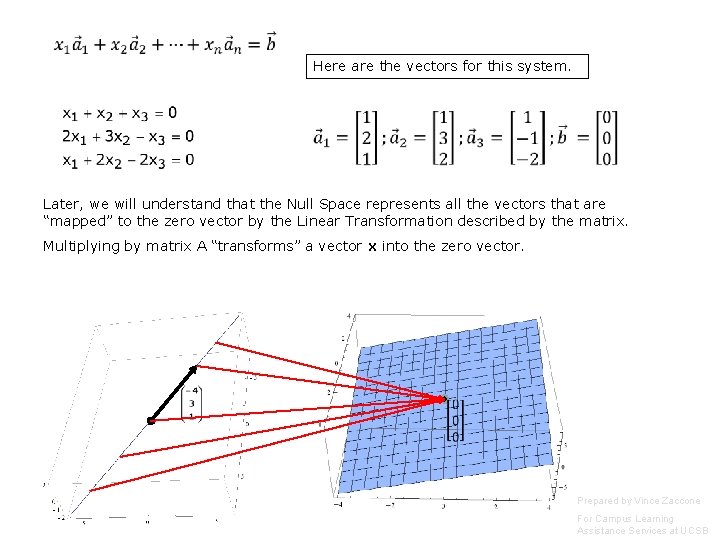
Here are the vectors for this system. Later, we will understand that the Null Space represents all the vectors that are “mapped” to the zero vector by the Linear Transformation described by the matrix. Multiplying by matrix A “transforms” a vector x into the zero vector. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Here are the vectors for this system. The vectors in the vector form of the equation are the columns of the matrix A in the matrix format. Row reduction yields: Here is the unique solution: This solution tells us the specific linear combination of a 1 a 2 and a 3 that adds up to the right side vector b. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

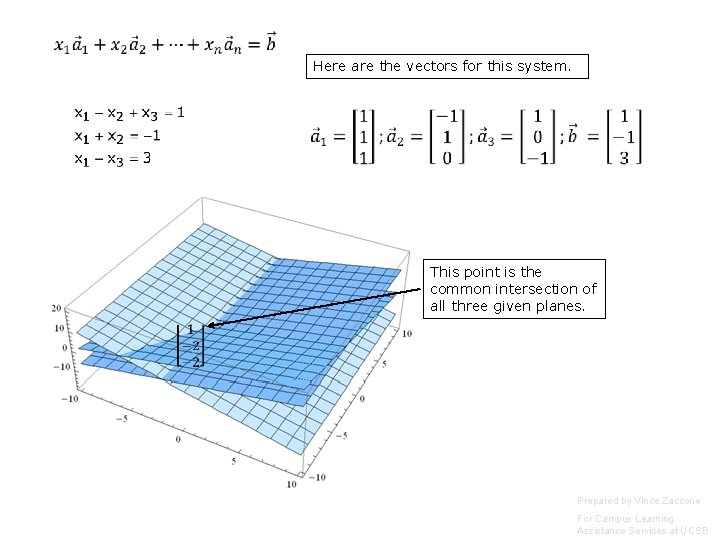
Here are the vectors for this system. This point is the common intersection of all three given planes. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Here are the vectors for this system. The vectors in the vector form of the equation are the columns of the matrix A in the matrix format. x 4 and x 5 are free variables Row reduction yields: Here is the corresponding solution. There are 2 free variables, so we get a 2 dimensional subset of ℝ 5. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB