Texture Mapping Aaron Bloomfield CS 445 Introduction to

Texture Mapping Aaron Bloomfield CS 445: Introduction to Graphics Fall 2006 (Slide set originally by David Luebke)

Overview Ø n n n n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 2

Texture Mapping: Motivation n n Scenes created with diffuse lighting look convincingly three-dimensional, but are flat, chalky, and “cartoonish” Phong lighting lets us simulate materials like plastic and (to a lesser extent) metal, but scenes still seem very cartoonish and unreal Big problem: polygons are too coarse-grained to usefully model fine surface detail Solution: texture mapping 3

Texture Mapping: Motivation n n Adding surface detail helps keep CG images from looking simple and sterile Explicitly modeling this detail in geometry can be very expensive n n Zebra stripes, wood grain, writing on a whiteboard Texture mapping pastes images onto the surfaces in the scene, adding realistic fine detail without exploding the geometry 4

5

Texture Mapping: Examples 6

Texture Mapping: Examples Doom III (ID Software) 7

Texture Mapping n n n In short: it is impractical to explicitly model fine surface detail with geometry Solution: use images to capture the “texture” of surfaces Texture maps can modulate many factors that affect the rendering of a surface n n n Color or reflectance (diffuse, ambient, specular) Transparency (smoke effects) What else? 8

Overview n Ø n n n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 9

Texture Mapping: Fundamentals n n A texture is typically a 2 -D image Can also be n n A 2 -D procedural texture A 3 -D procedural texture n n See video A 3 -D volumetric texture (rarely used) 10

Texture Mapping: Fundamentals n A texture is typically a 2 -D image n n Image elements are called texels Value stored at a texel affects surface appearance in some way n n Example: diffuse reflectance, shininess, transparency… The mapping of the texture to the surface determines the correspondence, i. e. , how the texture lies on the surface n n Mapping a texture to a triangle is easy (why? ) Mapping a texture to an arbitrary 3 -D shape is more complicated (why? ) 11

Texturing Fundamentals n n A texture is typically a 2 -D array of texels Mapping the texture to an arbitrary 3 -D shape is complex: 12
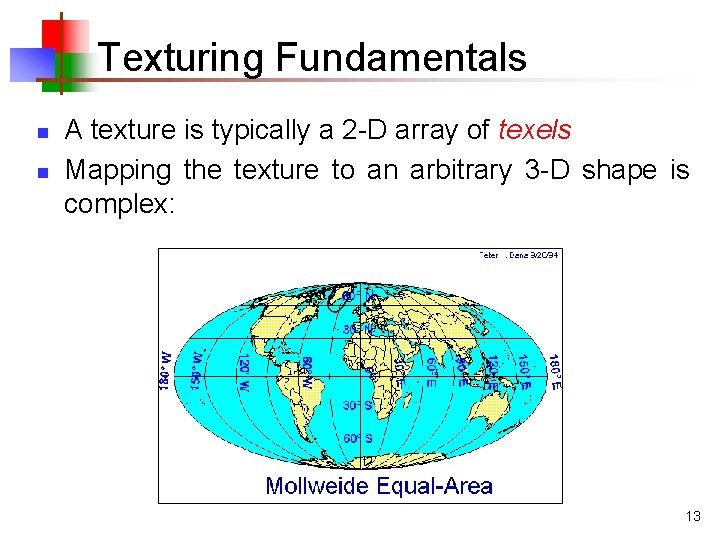
Texturing Fundamentals n n A texture is typically a 2 -D array of texels Mapping the texture to an arbitrary 3 -D shape is complex: 13

Texturing Fundamentals n n A texture is typically a 2 -D array of texels Mapping the texture to an arbitrary 3 -D shape is complex: 14

Texturing Fundamentals n n A texture is typically a 2 -D array of texels Mapping the texture to an arbitrary 3 -D shape is complex! http: //www. cs. virginia. edu/~gfx/Courses/2003/Intro. spring. 03/animations/unfold. mo v 15

How to map a texture n There a number of possibilities: n n n Flat Cube Tube (i. e. cylinder) Sphere The slides on the next slide are from http: //mediawiki. blender. org/index. php/Manual/Map_Input#2 D_to_3 D_Mapping 16
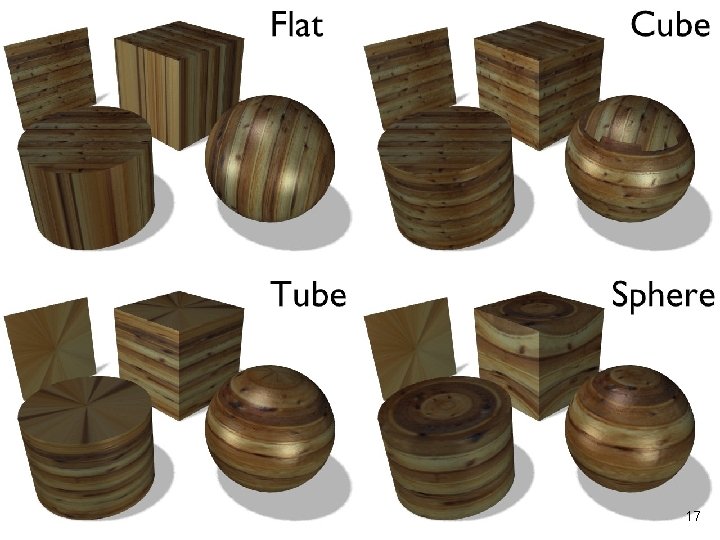
17

Overview n n Ø n n n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 18

Texture Mapping: Rendering n Rendering uses the mapping: n n n Find the visible surface at a pixel Find the point on that surface corresponding to that pixel Find the point in the texture corresponding to that point on the surface Use the parameters associated with that point on the texture to shade the pixel Using triangulated meshes reduces the problem to mapping a portion of the image to each triangle: 19
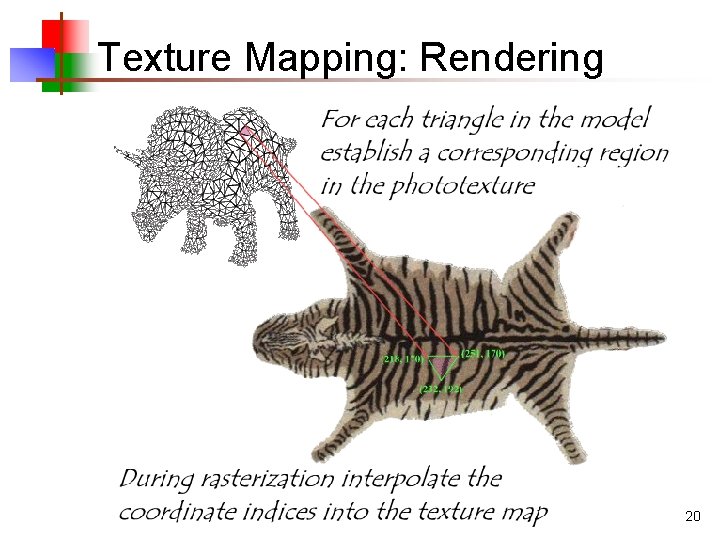
Texture Mapping: Rendering 20

Texture Mapping: User-Generated Mappings n For complex 3 -D objects, mapping textures is still something of an art…so we often let the user do it 21

Texture Mapping: Rendering n We typically parameterize the texture as a function in (u, v) n n For simplicity, normalize u & v to [0, 1] Associate each triangle with a texture Give each vertex of the triangle a texture coordinate (u, v) For other points on the triangle, interpolate texture coordinate from the vertices n n Much like interpolating color or depth But there’s a catch. . . 22

Naïve Texture Mapping n A first cut at a texture-mapping rasterizer: n For each pixel: n n Interpolate u & v down edges and across spans Look up nearest texel in texture map Color pixel according to texel color (possibly modulated by lighting calculations) Mc. Millan’s demo of this is at http: //graphics. lcs. mit. edu/classes/6. 837/F 98/Lecture 21/Slide 05. html n What artifacts do you see in this demo? 23

Naïve Texturing Artifacts n Another serious artifact is warping at the edges of triangles making up the mesh n A more obvious example: http: //graphics. lcs. mit. edu/classes/6. 837/F 98/Lecture 21/Slide 06. html n To address this, need to consider the geometry of interpolating parameters more carefully 24
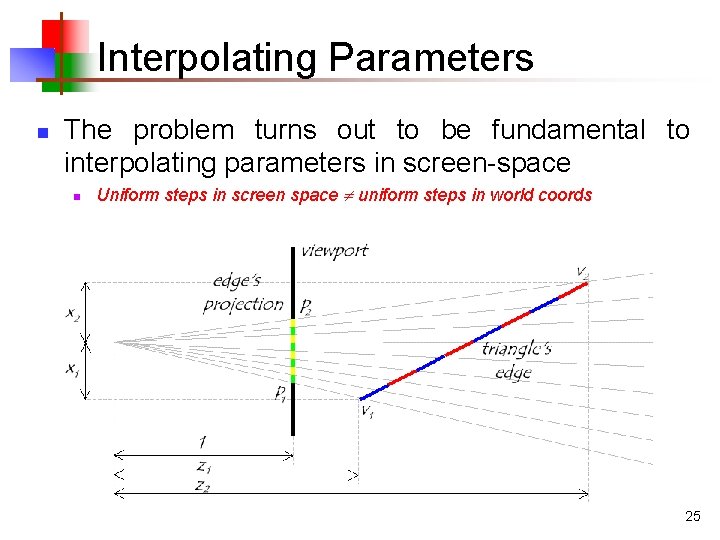
Interpolating Parameters n The problem turns out to be fundamental to interpolating parameters in screen-space n Uniform steps in screen space uniform steps in world coords 25

Interpolating Parameters n Perspective foreshortening is not getting applied to our interpolated parameters n n n Is this a problem with Gouraud shading? n n Parameters should be compressed with distance Linearly interpolating them in screen-space doesn’t do this Is everything I taught wrong? A: It can be, but we usually don’t notice (why? ) 26

Overview n n n Ø n n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 27

Perspective-Correct Interpolation n Skipping a bit of math to make a long story short… n n Rather than interpolating u and v directly, interpolate u/z and v/z n These do interpolate correctly in screen space n Also need to interpolate z and multiply per-pixel Problem: we don’t know z anymore Solution: we do know w 1/z So…interpolate uw and vw and w, and compute u = uw/w and v = vw/w for each pixel n This unfortunately involves a divide per pixel (Just 1? ) 28

Perspective-Correct Texturing n Known as perspective-correct texture mapping n Early PC cards and game consoles didn’t support it So how did they avoid the warping problem? n http: //graphics. lcs. mit. edu/classes/6. 837/F 98/Lecture 21/Slide 15. html n n As mentioned, other interpolation schemes really ought to use perspective correction n E. g. , Gouraud shading Generally get away without it because it is more important to be smooth than correct Java code fragment from Mc. Millan’s edgeequation triangle rasterizer: 29

Perspective-Correct Texturing: Code. . . Plane. Eqn(u. Plane, (u 0*w 0), (u 1*w 1), (u 2*w 2)); Plane. Eqn(v. Plane, (v 0*w 0), (v 1*w 1), (v 2*w 2)); Plane. Eqn(w. Plane, w 0, w 1, w 2); . . . for (y = y. Min; y <= y. Max; y += raster. width) { e 0 = t 0; e 1 = t 1; e 2 = t 2; u = tu; v = tv; w = tw; z = tz; boolean been. Inside = false; for (x = x. Min; x <= x. Max; x++) { if ((e 0 >= 0) && (e 1 >= 0) && (e 2 >= 0))) { int iz = (int) z; if (iz <= raster. zbuff[y+x]) { float denom = 1. 0 f / w; int uval = (int) (u * denom + 0. 5 f); uval = tile(uval, texture. width); int vval = (int) (v * denom + 0. 5 f); vval = tile(vval, texture. height); int pix = texture. get. Pixel(uval, vval); if ((pix & 0 xff 000000) != 0) { raster. pixel[y+x] = pix; raster. zbuff[y+x] = iz; } } been. Inside = true; } else if (been. Inside) break; e 0 += A 0; e 1 += A 1; e 2 += A 2; z += Az; u += Au; v += Av; w += Aw; } t 0 += B 0; t 1 += B 1; t 2 += B 2; tz += Bz; tu += Bu; tv += Bv; tw += Bw; } 30

Texture Tiling n n It is often handy to tile a repeating texture pattern onto a surface The previous code does this via tile(): int uval = (int) (u * denom + 0. 5 f); uval = tile(uval, texture. width); int vval = (int) (v * denom + 0. 5 f); vval = tile(vval, texture. height); int pix = texture. get. Pixel(uval, vval); int tile(int val, int size) { while (val >= size) val -= size; while (val < 0) val += size; } See http: //graphics. lcs. mit. edu/classes/6. 837/F 98/Lecture 21/Slide 18. html 31

Overview n n Ø n n n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 32

Texture Transparency n Mc. Millan’s code also includes a “quick fix” for handling transparent texture: if ((pix & 0 xff 000000) != 0) { raster. pixel[y+x] = pix; raster. zbuff[y+x] = iz; } n n Note that this doesn’t handle partial transparency (How might such partial transparency arise? ) Demo at: http: //graphics. lcs. mit. edu/classes/6. 837/F 98/Lecture 21/Slide 19. html 33

34

Texture Map Aliasing n Naive texture mapping looks blocky, pixelated n Problem: using a single texel to color each pixel: int uval = (int) (u * denom + 0. 5 f); int vval = (int) (v * denom + 0. 5 f); int pix = texture. get. Pixel(uval, vval); n Actually, each pixel maps to a region in texture n n If the pixel is larger than a texel, we should average the contribution from multiple texels somehow If the pixel is smaller than a texel, we should interpolate between texel values somehow Even if pixel size texel size, a pixel will in general fall between four texels An example of a general problem called aliasing 35

Texture Map Antialiasing n Use bilinear interpolation to average nearby texel values into a single pixel value (Draw it) n Find 4 nearest texture samples n n Round u & v up and down Interpolate texel values in u Interpolate resulting values in v Also addresses the problem of many pixels projecting to a single texel (Why? ) 36

Texture Map Antialiasing n What if a single pixel covers many texels? n Problem: sampling those texels at a single point (the center of the pixel): n n Produces Moire patterns in coherent texture (checkers) Leads to flicker or texture crawling as the texture moves 37

Moire Patterns 38

Texture Map Antialiasing n What if a single pixel covers many texels? n Approach: blur the image under the pixel, averaging the contributions of the covered texels n n But calculating which texels every pixel covers is way too expensive, especially as the texture is compressed Solution: pre-calculate lower-resolution versions of the texture that incorporate this averaging 39

Overview n n n Ø n n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 40
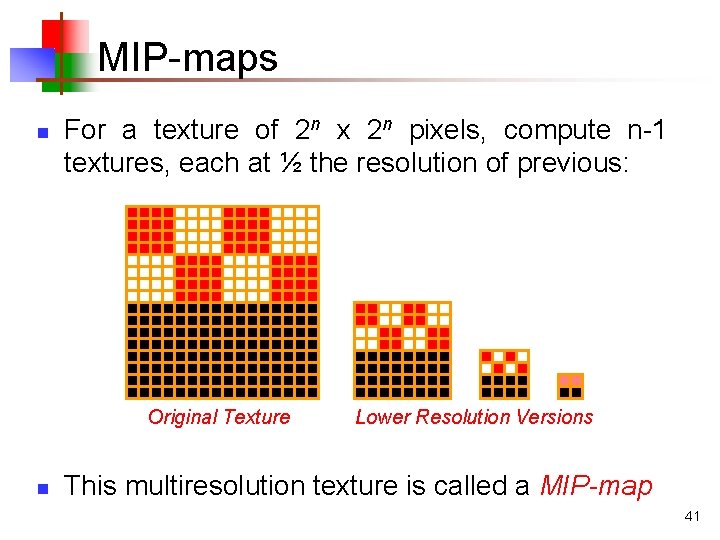
MIP-maps n For a texture of 2 n x 2 n pixels, compute n-1 textures, each at ½ the resolution of previous: Original Texture n Lower Resolution Versions This multiresolution texture is called a MIP-map 41

Generating MIP-maps n Generating a MIP-map from a texture is easy n n n For each texel in level i, average the values of the four corresponding texels in level i-1 If a texture requires n bytes of storage, how much storage will a MIP-map require? Answer: 4 n/3 42

Representing MIP-maps R G R G B B Trivia: MIP = Multum In Parvo (many things in a small place) 43

Using MIP-maps n Each level of the MIP-map represents a pre-blurred version of multiple texels n n A texel at level n represents 2 n original texels When rendering: n n n Figure out the texture coverage of the pixel (i. e. , the size of the pixel in texels of the original map) Find the level of the MIP map in which texels average approximately that many original texels Interpolate the value of the four nearest texels 44

Using MIP-maps n Even better: n n Likely, the coverage of the pixel will fall somewhere between the coverage of texels in two adjacent levels of the MIP map Find the pixel’s value in each of the two textures using two bilinear interpolations Using a third interpolation, find a value in between these two values, based on the coverage of the pixel versus each of the MIP-map levels This is (misleadingly? ) called trilinear interpolation 45

MIP-map Example n No filtering: n MIP-map texturing: 46

Can We Do Better? n n What assumption does MIP-mapping implicitly make? A: The pixel covers a square region of the texture n n More exactly, the compression or oversampling rate is the same in u and v Is this a valid assumption? Why or why not? 47

MIP-maps and Signal Processing n An aside: aliasing and antialiasing are properly topics in sampling theory n n Nyquist theorem, convolution and reconstruction, filters and filter widths Textures are particularly difficult because a tiled texture can easily generate infinite frequencies n n E. g. , a checkered plane receding to an infinite horizon Using a MIP-map amounts to prefiltering the texture image to reduce artifacts caused by sampling at too low a rate 48

Summed-Area Tables n A technique called summed-area tables lets us integrate texels covered by the pixel more exactly (but still quickly) n n Details in the book Example: MIP-map texturing Summed-area table texturing 49

Overview n n n Ø n Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 50

Texture Mapping Variations n In addition to the texture, we add the lighting model also: Texture as R, G, B: Texture with lighting: 51

Bump Mapping n The texture map can modulate the surface normal used for shading Sphere w/ diffuse texture Swirly bump map Sphere w/ diffuse texture and swirly bump map 52
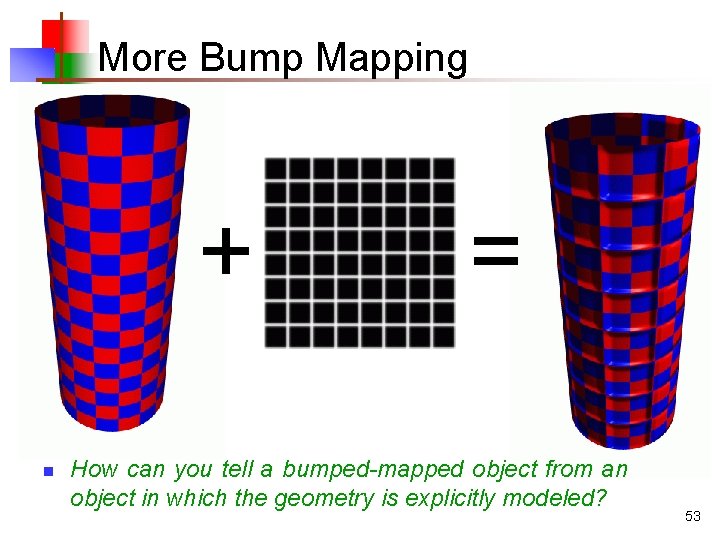
More Bump Mapping + n = How can you tell a bumped-mapped object from an object in which the geometry is explicitly modeled? 53

Another Bump Mapping Example n From Wikipedia + = 54

Displacement Map n A displacement map actually displaces the geometry n n Treats the texture as a height field to be applied to the surface Starting to appear in the interactive graphics pipeline n n First supported in Matrox Parhelia card Can sort of implement with beta drivers in ATI & NVIDIA cards Will soon appear in all cards Implemented by recursive subdivision of triangles/quads 55
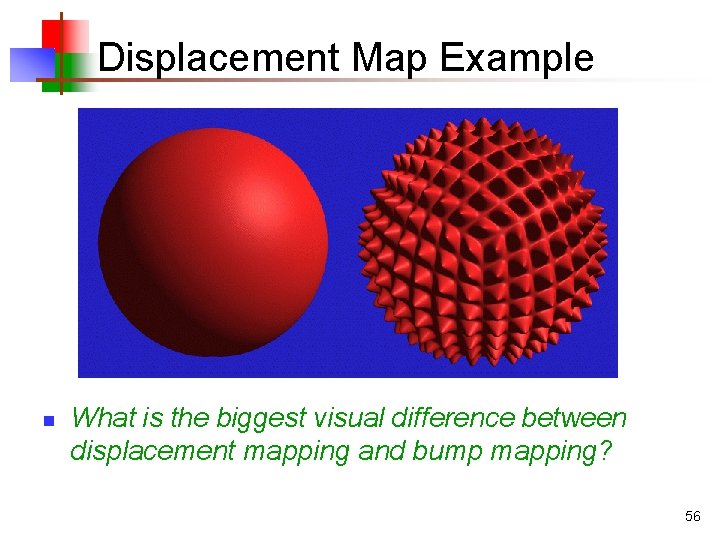
Displacement Map Example n What is the biggest visual difference between displacement mapping and bump mapping? 56

Overview n n n n Ø Motivation and Examples Fundamentals Algorithms Perspective-Correct Texturing Transparency and Anti-Aliasing MIP-Maps Bump and Displacement Maps Illumination Maps 57

Illumination Maps n Quake introduced illumination maps or light maps to capture lighting effects in video games Texture map: Light map Texture map + light map: 58

Illumination Maps n Illumination maps differ from texture maps in that they: n n Usually apply to only a single surface Are usually fairly low resolution Usually capture just intensity (1 value) rather than color (3 values) Illumination maps can be: n n Painted by hand: Disney’s Aladdin ride Calculated by a global illumination process: Nintendo 64 demo, modern level builders 59

Other Texture Applications n Lots of other interesting applications of the texturemap concept (we’ll return to some): n n n Shadow maps 3 -D textures (marble, wood, clouds) Procedural textures Environment maps & cube maps For a neat explanation of the first three (with cool applets, as usual) check out: http: //graphics. lcs. mit. edu/classes/6. 837/F 98/Lecture 22/Slide 21. html 60
- Slides: 60



















































































