Teora de Errores Topografa Introduccin En la vida

Teoría de Errores Topografía

Introducción • En la vida cotidiana la mayoría de las personas están acostumbradas a contar, pero no así a realizar mediciones. • La cantidad de personas presentes en este salón son p. e. 23, 36 y no 32. 9 • La topografía se encarga de medir cantidades cuyo valor exacto o verdadero no se puede determinar, como el caso de distancias, elevaciones, volúmenes.

Principio fundamental de la topografía Ninguna medición es exacta y nunca se conoce el valor verdadero de la cantidad que se mide.

• Aunque nunca se conocer el valor exacto de una cantidad que se mide, podemos saber de forma exacta cual debe ser la suma de un grupo de mediciones, p. e. la suma de los 3 ángulos internos de un triángulo debe ser igual a 180º, y la suma de los 4 ángulos internos de un rectángulo debe ser 360º y así sucesivamente.

• Sin embargo, se debe tener habilidad para ejecutar mediciones precisas, esto resulta obvio cuando pensamos en largos puentes, túneles, edificios altos, etc. ; pero también es necesario la precisión en los levantamientos topográficos.

Exactitud y Precisión • Exactitud, se refiere al grado de perfección que se obtiene en las mediciones. Representa que tan cerca se encuentra una medición determinada del valor verdadero. • Precisión, es el grado de refinamiento con el que se mide una determinada cantidad, es la cercanía de una medida a otra, si se mide una cantidad y los valores son muy cercanos entre sí, la precisión es alta.

Errores y Equivocaciones • No existe persona que tenga los sentidos tan desarrollados para medir cantidades de forma exacta y tampoco instrumentos con los cuales lograrlo, en consecuencia, todas las mediciones son imperfectas. • De esta forma, las diferencias entre las cantidades medidas y sus magnitudes verdaderas se conocen como errores o equivocaciones.

• Equivocaciones, es una diferencia con respecto al valor verdadero, causada por la falta de atención, pero puede eliminarse haciendo una revisión cuidadosa. • Error, es una diferencia respecto al valor verdadero, ocasionado por la imperfección de los sentidos de las personas, de los instrumentos usados o por efectos climáticos.

Fuentes de error • Las personas Los sentidos no son perfectos • Instrumentos Los instrumentos no son perfectos • Naturales Ocasionados por cambios de temperatura, viento y humedad

Clasificación de los errores • Errores groseros Producto de la falta de concentración del operador del equipo. • Errores sistemáticos Producto de la presencia de errores físicos o matemáticos, siempre se conoce su influencia, por lo general son pequeños. • Errores aleatorios o accidentales Obedecen a la falta de perfección de los elementos que conforman los instrumentos.

Tipos de errores accidentales • Error verdadero (Ei) Representa la diferencia entre el valor verdadero y el error medido. Ei = x – li X = Valor verdadero li = Medición

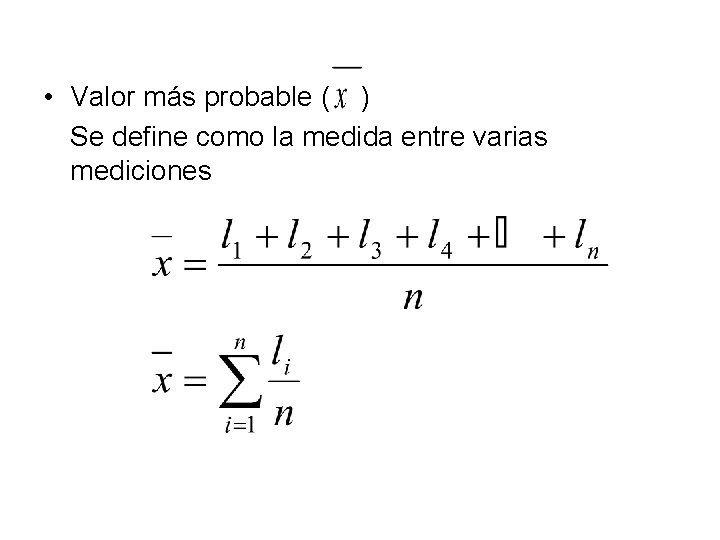
• Valor más probable ( ) Se define como la medida entre varias mediciones

• Error aparente ( i) Representa la diferencia entre el valor más probable de un grupo de mediciones y la medida en sí. Es el residuo de una observación individual (grado en que se desvía o aparta del promedio la cantidad). i= - li Si se tiene l 1, l 2, l 3, l 4, l 5 El valor más probable 1= 2= 3= 4= - l 1 Error aparente de la primera medición - l 2 Error aparente de la segunda medición - l 3 Error aparente de la tercera medición - l 4 Error aparente de la cuarta medición

Ejercicio Calcular el error aparente de las siguientes mediciones …. l 1=10, 20 m l 2=10, 30 m

• Error estándar (σ) y varianza (σ2) Son términos estadísticos que se emplean para expresar la precisión de un grupos de medidas. La ecuación de la desviación estándar es: σ es la desviación estándar error aparente es la suma de los cuadrados de los residuos individuales n es el número de observaciones La varianza es igual a σ2, el cuadrado de la desviación estándar.

“En topografía se considera a toda desviación como un error, y por ello normalmente se usa la expresión error estándar en vez de desviación estándar”

Interpretación del error estándar El error estándar establece los límites dentro de los cuales debe esperarse que caigan las mediciones 68. 27% de las veces. En otras palabras, si se repitió 10 veces una medición, debería esperarse que aproximadamente 7 de los resultados queden dentro de los límites establecidos por el error estándar y 3 de ellos caerían fuera de dichos límites. Otra interpretación es que una medición adicional tendría 68. 27% de probabilidad de caer dentro de los límites establecidos por el error estándar. Una tercera deducción es que el valor real o verdadero tiene 68. 27% de probabilidades de caer dentro de los límites del error estándar.

Errores de 50, 90 y 95% Se puede determinar la probabilidad de un error de cualquier porcentaje de probabilidad mediante la siguiente ecuación general. Ep=Cpσ En la cual Ep es el porcentaje de error y Cp es un factor numérico.

E 50 = 0, 6745σ E 90 = 1, 6449σ E 95 = 1, 9599σ El error de 50% (E 50) es el llamado error probable. Este valor establece los límites dentro de los cuales han de caer las mediciones 50% de las veces. En otras palabras, una medida tendrá la misma probabilidad de quedar dentro de estos límites que de caer fuera de ellos.

Ejemplo Supóngase que se ha medido 10 veces una línea, con los resultados a continuación. Se supone que estas mediciones ya se han corregido por todos los errores sistemáticos.

Pueden deducirse las siguientes conclusiones: 1. La longitud más probable es 1000, 45 m. 2. El error estándar de una sola medida es ± 0, 08 m. 3. La expectativa normal es que 68% de las veces, una longitud registrada estaría comprendida entre 1000, 37 y 1000, 53 m; es decir, que aproximadamente siete de los valores estarían comprendidos dentro de estos límites. (Realmente siete lo están. ) 4. El error probable (E 50) es ± 0, 05 m. Por tanto, puede anticiparse que la mitad, o sea cinco, de las medidas caerán dentro del intervalo 1000, 40 a 1000, 50. (Cuatro valores quedan ahí). 5. 90% de las veces una longitud medida no contendrá un error mayor de ± 0, 13 m, y su valor estaría dentro del intervalo de 1000, 32 y 1000, 58

6. El error de 95% sería ± 0, 15, y la longitud estaría comprendida entre 1000, 30 y 1000, 60 en el 95% de las veces. (Nótese que todas las medidas están, por cierto, dentro de los límites de ambos errores, el de 90% y el de 95%.

• Error de una suma La expresión para determinar el error de una suma de cantidades observadas independientemente es: En la cual E representa cualquier error específico; a, b y c son las medidas independiente.

Ejemplo Se mide una línea en tres partes, siendo los errores de éstas iguales a: ± 0, 012; ± 0, 028; y ± 0, 020 El error de la longitud total es: Se aplica un cálculo similar al error de cualquier producto, y en consecuencia, al error de un área.

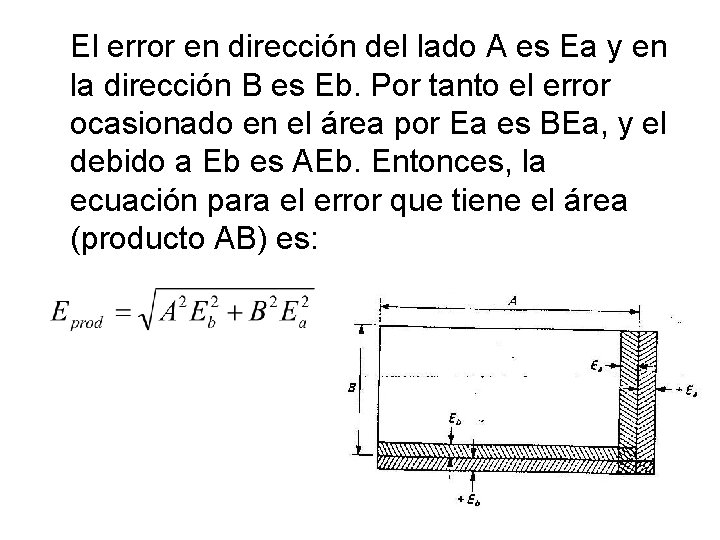
El error en dirección del lado A es Ea y en la dirección B es Eb. Por tanto el error ocasionado en el área por Ea es BEa, y el debido a Eb es AEb. Entonces, la ecuación para el error que tiene el área (producto AB) es:

Ejemplo Para un lote rectangular de 50, 00 ± 0, 01 x 100, 00 ± 0, 02 metros, el error que hay en el área es

• Error de una serie A veces se lee una serie de cantidades similares, como los ángulos de una poligonal, resultando cada medida con un error de aproximadamente la misma magnitud en todos los casos. Al error total de la suma de todas las cantidades medidas de una serie de esta naturaleza se le llama error de la serie, y se le designa por Eserie. En donde E representa al error en cada medida y n es el número de mediciones.

Ejemplo Supóngase que se mide con cinta de 50 m. , una distancia igual a 1 km, aplicando ciertas técnicas, se efectúa cada medición de 50 m con un error de ± 0, 005 m. Se desea conocer el error que se comete en la medición de 1 km.

• Error medio (εm) Ei = Error verdadero n = Número de errores verdaderos

• Error relativo Es una manera de expresar el error, con el fin de hacerlo más notable, se expresa en forma de fracciones. Por ejemplo, un error de diez (10) medidas cada cincuenta (50) significa que nos hemos equivocado 10 veces en 50 medidas realizadas.

Cifras significativas • Al registrar medidas, una indicación de la exactitud lograda es el número de dígitos (cifras significativas) que se registran. Por definición, el número de cifras significativas en cualquier valor incluye los dígitos positivos más uno que es un dígito estimado, y por tanto, cuestionable.

Por ejemplo. Una distancia registrada como 873, 52 se dice que tiene cinco cifras significativas; en este caso, los cuatro primeros dígitos son seguros y el último es cuestionable. Para ser congruentes con la teoría de errores, es esencial que los datos se registren con el número correcto de cifras significativas, si se descarta una cifra significativa al registrar un valor, se ha desperdiciado el tiempo empleado en lograr exactitud.

• A menudo, se confunde el número de cifras significativas con el número de cifras decimales. • Puede tener que usarse cifras decimales para conservar el número correcto de cifras significativas, pero aquéllas no indican por sí mismas las cifras significativas.

Ejemplo ü Dos cifras significativas: 24; 2, 4; 0, 24, 0, 0024, 0, 020 ü Tres cifras significativas: 364; 36, 4; 0, 000364; 0, 0240 ü Cuatro cifras significativas: 7621; 76, 21; 0, 0007621; 2. 400

• Para hacer una adición o sustracción debe redondearse la respuesta, reteniendo como última cifra significativa al dígito que se encuentra en la columna completa de cifras significativas que está más a la derecha. 46, 4012 57, 301 1, 02 1, 48 375, 0 629 422, 4 688

Redondeo de números Es el proceso de suprimir uno o más dígitos para que la respuesta sólo contenga aquéllos que sean significativos o necesarios en cálculos subsecuentes. Para tal efecto puede seguirse el procedimiento a continuación. 1. Cuando el dígito a despreciar sea menor a 5, se escribirá el número sin ese dígito. Así, 78, 374 se transforma en 78, 37. 2. Cuando el dígito a despreciar sea exactamente 5, se usará el siguiente número para el dígito precedente. Así, 78, 375 se transforma en 78, 38 y 78, 385 se redondeará también a 78, 38. 3. Cuando el dígito a despreciar sea mayor que 5, se escribirá el número con el dígito precedente aumentado en una cantidad. Así 78, 376 se convierte en 78, 38.

Aparición de errores aleatorios Supóngase que se realiza una medida de distancia de 10, 46 pulgadas con una escala en la que puede estimarse una lectura al centésimo, y que es correcta a ± 0, 05. en este caso, el valor real de la medida está comprendido entre 10, 41 y 10, 51; pudiendo ser: 10, 41; 10, 42; 10, 43, 10, 44; 10, 45; 10, 46; 10, 47; 10, 48; 10, 49; 10, 50; ó 10, 51. En consecuencia hay 11 posibles valores para la respuesta correcta. Este análisis puede suponer que todas lecturas tienen la misma posibilidad de ser correctas. La probabilidad de que cualquier respuesta sea correcta es, por tanto, de 1/11 ó 0, 0909.

Considérese una línea que requiere que se hagan dos medidas adyacentes con esta escala, teniendo cada una el mismo error posible. La respuesta, que es la suma de dos medidas, puede ser el total de cualquier par de 11 posibilidades para cada medición separada, teniendo todas igual probabilidad de ser correctas. Según los principios matemáticos, si un evento puede ocurrir de n maneras y otro de r modos, los dos eventos juntos pueden ocurrir de nr maneras. En las condiciones supuestas hay (11 x 11)=121 posibilidades. Al sumar las dos medidas el valor real estará comprendido entre -0, 10 y +0, 10. Sólo un par de posibles valores puede dar una diferencia de -0, 10, y ese es el para el cual la diferencia en cada medida es -0, 05.

Puede obtenerse un error de -0, 09 en dos formas, y es posible que haya una diferencia de -0, 05 en la primera lectura y una diferencia de -0, 04 en la segunda lectura, o bien, una diferencia de -0, 04 en la primera y una diferencia de -0, 05 en la segunda. Este análisis puede continuarse hasta obtener los siguientes resultados.

Si se toman tres medidas adyacentes de la misma manera, con una diferencia máxima de -0, 05 y +0, 05; las tres tendrían que estar fuera de realidad en -0, 05 ó +0, 05 para obtener una amplitud de error de -0, 15 a +0, 15 y por los principios matemáticos, el número total de probabilidades es 11 x 11=1331.

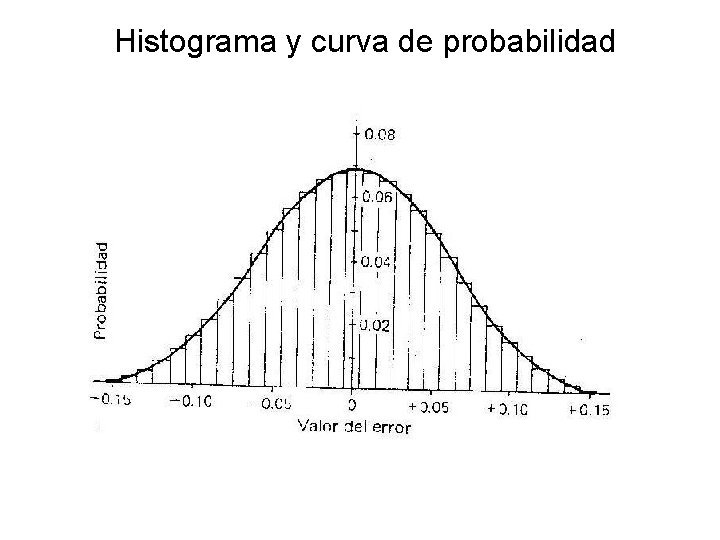
Histograma y curva de probabilidad