Temperature in relativistic dissipative fluids P Vn Department

















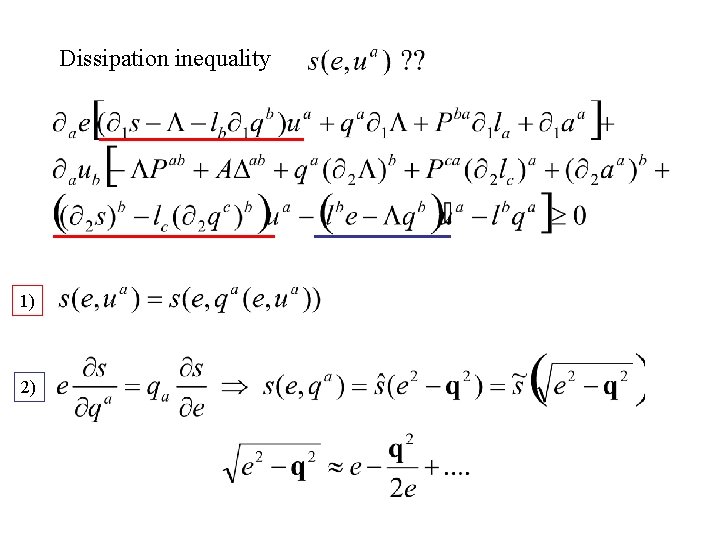









- Slides: 36

Temperature in relativistic dissipative fluids P. Ván Department of Theoretical Physics Research Institute of Particle and Nuclear Physics, Budapest, Hungary – Motivation Internal energy: – Problems with second order theories – Thermodynamics, fluids and stability – Generic stability of relativistic dissipative fluids – Temperature of moving bodies – Summary

Dissipative relativistic fluids Nonrelativistic Relativistic Local equilibrium (1 st order) Fourier+Navier-Stokes Eckart (1940), Tsumura-Kunihiro (2008) Beyond local equilibrium (2 nd order) Cattaneo-Vernotte, gen. Navier-Stokes etc… Israel-Stewart (1969 -72), Pavón-extended, Müller-Ruggieri, Geroch, Öttinger, Carter, etc. Eckart: Extended (Israel–Stewart – Pavón–Jou–Casas-Vázquez): (+ order estimates)

Remarks – The extended theories are not proved to be symmetric hyperbolic. – In Israel-Stewart theory the symmetric hyperbolicity conditions of the perturbation equations follow from the stability conditions. – Parabolic theories cannot be excluded – speed of the validity range can be small. They can be extended. – Fourier-Navier-Stokes limit. Relaxation to the (unstable) first order theory? (Geroch 1995, Lindblom 1995) – Generic stability is important.

Fourier-Navier-Stokes p Isotropic linear constitutive relations, <> is symmetric, traceless part Equilibrium: Linearization, …, Routh-Hurwitz criteria: Thermodynamic stability (concave entropy) Hydrodynamic stability

Stability and Second Law: Non-equilibrium thermodynamics: basic variables evolution equations (basic balances) Second Law Stability of homogeneous equilibrium Entropy ~ Lyapunov function Homogeneous systems (equilibrium thermodynamics): dynamic reinterpretation – ordinary differential equations clear, mathematically strict See e. g. Matolcsi, T. : Ordinary thermodynamics, Academic Publishers, 2005 Continuum systems partial differential equations – Lyapunov theorem is more technical Linear stability (of homogeneous equilibrium)

Stability conditions of the Israel-Stewart theory (Hiscock-Lindblom 1985)

Special relativistic fluids (Eckart): energy-momentum density particle density vector qa – momentum density or energy flux? ? General representations by local rest frame quantities. Eckart term

Second Law (Liu procedure) – first order weakly nonlocal: Entropy inequality with the conditions of energy-momentum and particle number balances as constraints: Consequences: State space: 1) 2) 3) Ván: JMMS, 2008, 3/6, 1161, (ar. Xiv: 07121437)

Modified relativistic irreversible thermodynamics: Internal energy: Eckart term

1) Thermostatics: Temperatures and other intensives are doubled: Different roles: Equations of state: Constitutive functions: Θ, M T, μ

2) Quasy-hyperbolic extension – relaxation of viscosity: Relaxation: There are no β derivatives.

Dissipative hydrodynamics < > symmetric traceless spacelike part linear stability of homogeneous equilibrium CONDITION: thermodynamic stability

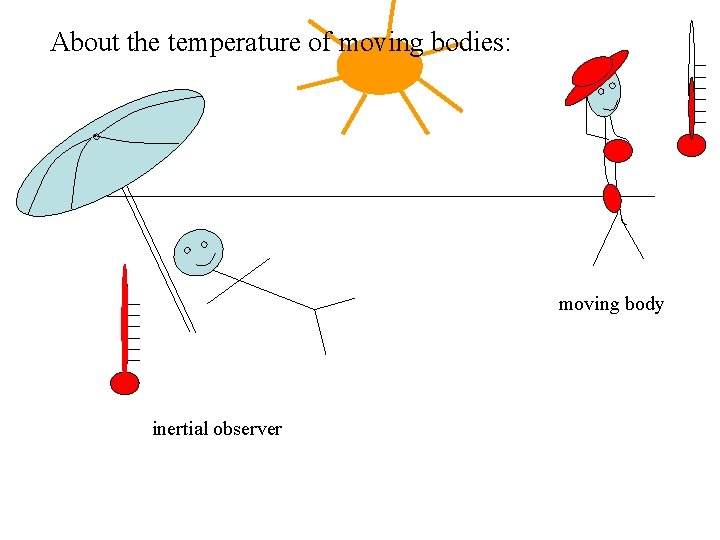
About the temperature of moving bodies: moving body inertial observer

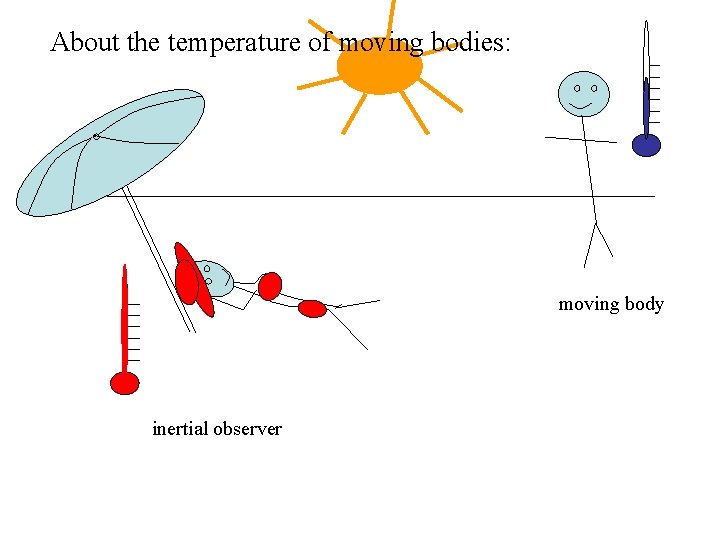
About the temperature of moving bodies: moving body inertial observer

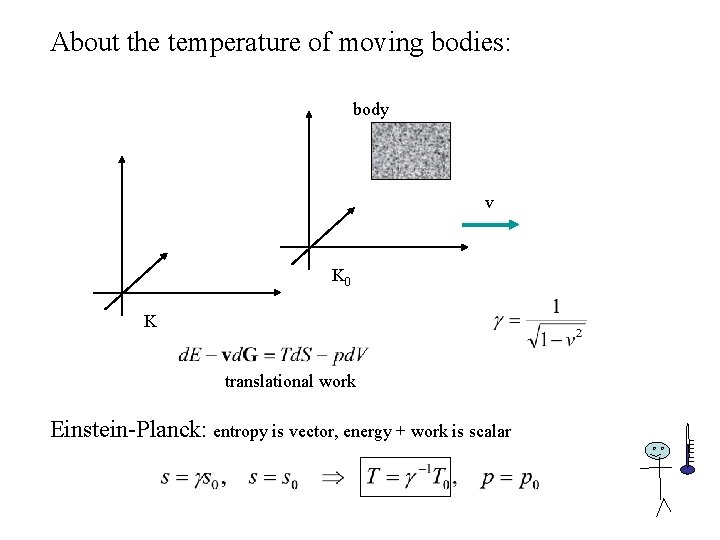
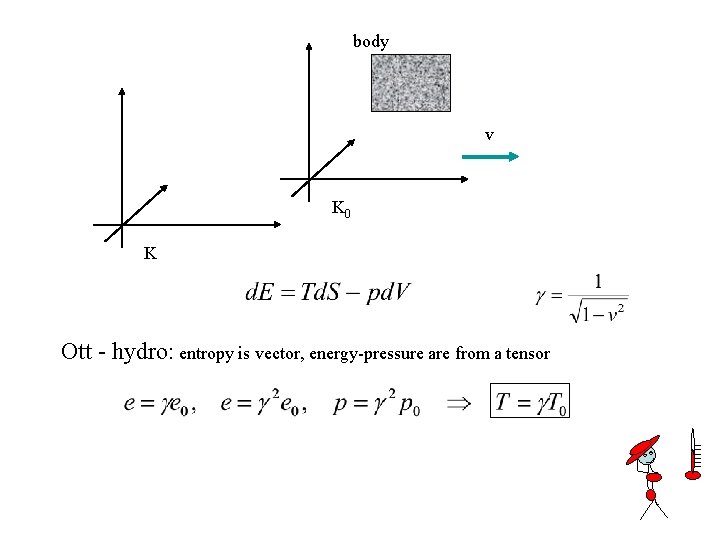
About the temperature of moving bodies: body v K 0 K translational work Einstein-Planck: entropy is vector, energy + work is scalar

body v K 0 K Ott - hydro: entropy is vector, energy-pressure are from a tensor

Integration, homogeneity: Ea energy-momentum vector Landsberg Einstein-Planck Ott

Hovewer, Gibbs relation gives more than the transformation properties! The real question is: Two bodies A and B have relative speed v. What must be the relation between their temperatures TA and TB, measured in their rest frames, if they are to be in thermal equilibrium? Thermal interaction requires uniform velocities. …

Summary – Extended – theories are not ultimate. energy ≠ internal energy → generic stability without extra conditions – hyperbolic(-like) extensions, solutions /Bíró, Molnár and Ván: PRC, (2008), 78, 014909 (ar. Xiv: 0805. 1061)/ – different temperatures in Fourier-law (equilibration) and in state functions out of local equilibrium → interpretation – general arguments (no Boltzmann) → universality

Thank you for your attention!

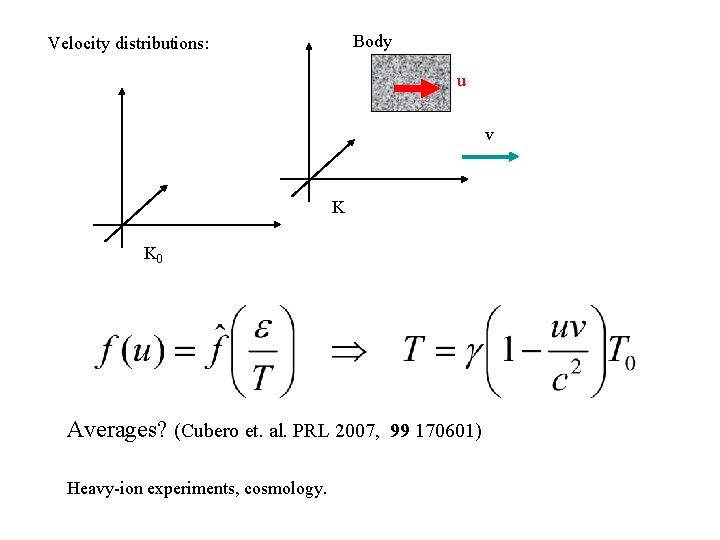
Body Velocity distributions: u v K K 0 Averages? (Cubero et. al. PRL 2007, 99 170601) Heavy-ion experiments, cosmology.

Liu procedure for relativistic fluids Thermodynamics – local rest frame – basic state (fields): – constitutive state: – constitutive functions: 4 -vector (temperature ? ) Solution of Liu equations ( are local):
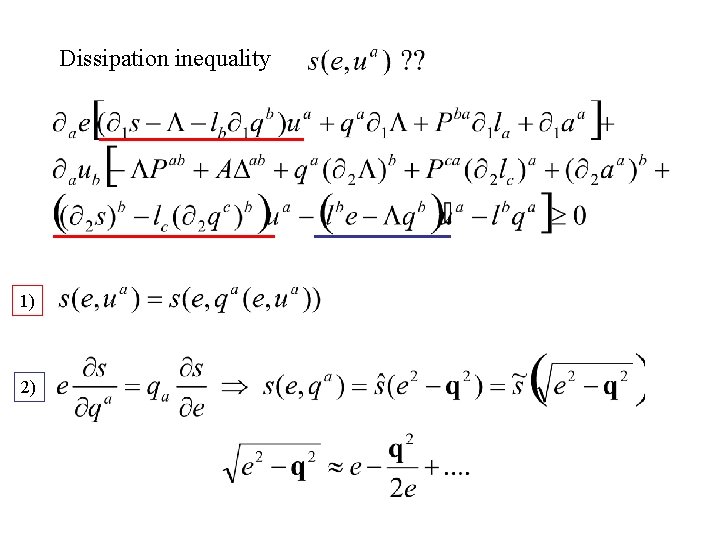
Dissipation inequality 1) 2)

Energy-momentum – momentum density and energy flux Landau choice:

Linearization

exponential plane-waves

Routh-Hurwitz: thermodynamic stability

Causality hyperbolic or parabolic? Well posedness Speed of signal propagation Hydrodynamic range of validity: ξ – mean free path τ – collision time Water at room temperature: More complicated equations, more spacetime dimensions, ….

Remarks on hyperbolicity 1) Hyperbolicity does not result in automatic causality, because the propagation speed of small perturbations can be large. hyperbolic causal 2) Parabolic equations and first order theories are not automatically excluded. The validity range of theory could prevent large speeds if the perturbations were relaxing fast. parabolic+stable causal 3) Instability in first order theories is not acceptable. Second order dissipative theories are corrections to first order stable theories.

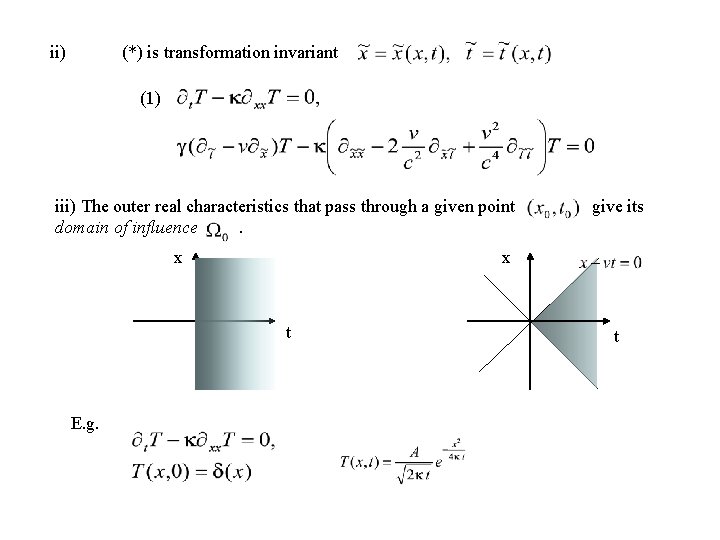
Causality hyperbolic or parabolic? Well posedness Speed of signal propagation Second order linear partial differential equation: Corresponding equation of characteristics: i) Hyperbolic equation: Parabolic equation: Elliptic equation: two distinct families of real characteristics one distinct families of real characteristics no real characteristics Well posedness: existence, unicity, continuous dependence on initial data. A characteristic Cauchy problem of (1) is well posed. (initial data on the characteristic surface: )

ii) (*) is transformation invariant (1) iii) The outer real characteristics that pass through a given point domain of influence. x x t E. g. give its t

Infinite speed of signal propagation? physics - mathematics Hydrodynamic range of validity: ξ – mean free path τ – collision time Water at room temperature: Fermi gas of light quarks at : More complicated equations, more spacetime dimensions, ….

Non-relativistic fluid mechanics local equilibrium, Fourier-Navier-Stokes n vi e qi Pij ki Thermodynamics p particle number density relative (3 -)velocity internal energy density internal energy (heat) flux pressure momentum density

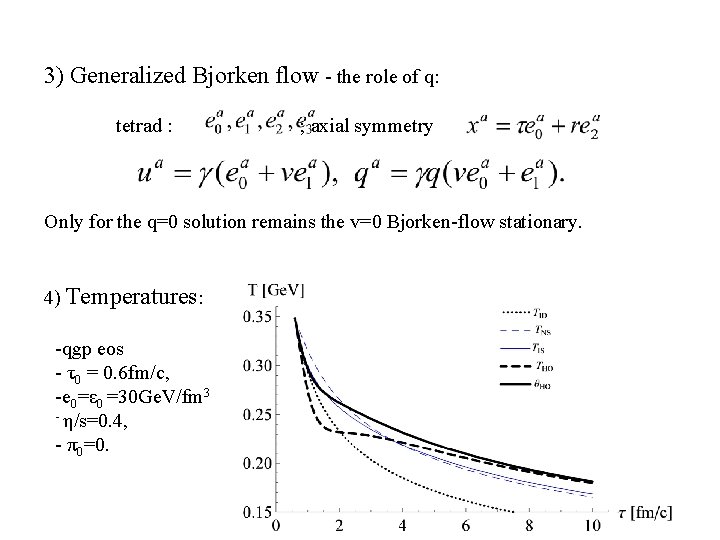
3) Generalized Bjorken flow - the role of q: tetrad : ; axial symmetry Only for the q=0 solution remains the v=0 Bjorken-flow stationary. 4) Temperatures: -qgp eos - τ0 = 0. 6 fm/c, -e 0=ε 0 =30 Ge. V/fm 3 - η/s=0. 4, - π0=0.

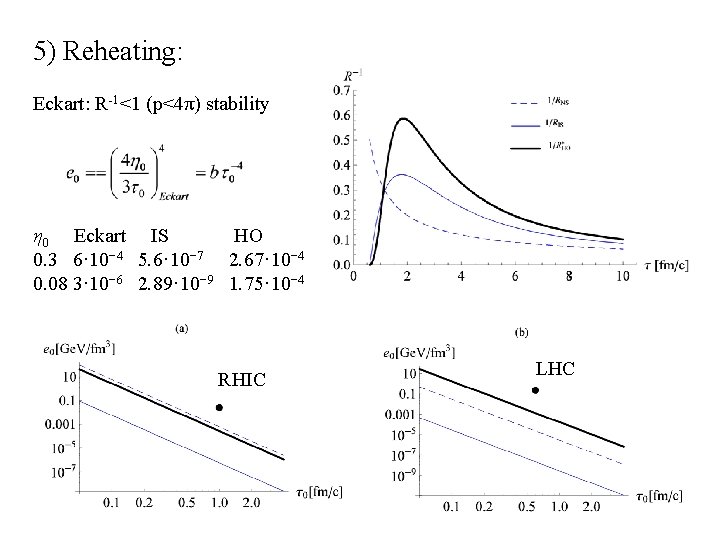
5) Reheating: Eckart: R-1<1 (p<4π) stability η 0 Eckart IS HO 0. 3 6· 10− 4 5. 6· 10− 7 2. 67· 10− 4 0. 08 3· 10− 6 2. 89· 10− 9 1. 75· 10− 4 RHIC LHC

About the temperature of moving bodies: moving body Sardegna inertial observer
 Forze dissipative
Forze dissipative Relativistic mean field theory
Relativistic mean field theory Cognitive-affective complexity
Cognitive-affective complexity Relativistic thinking example
Relativistic thinking example Relative speed of approach
Relative speed of approach Relativistic momentum
Relativistic momentum Relativistic doppler effect ppt
Relativistic doppler effect ppt Relativistic kinetic energy
Relativistic kinetic energy Length contraction
Length contraction Relativistic kinetic energy
Relativistic kinetic energy Relativistic equations of binet
Relativistic equations of binet Relativistic thinking example
Relativistic thinking example Relativistic momentum
Relativistic momentum Kinetic energy of a relativistic particle
Kinetic energy of a relativistic particle Bertrand postulate
Bertrand postulate Reflective and relativistic thinking
Reflective and relativistic thinking Derivation of relativistic mass
Derivation of relativistic mass Relativistic circular motion
Relativistic circular motion Kinetic energy of a relativistic particle
Kinetic energy of a relativistic particle General relativity equation
General relativity equation Difference between curie temperature and neel temperature
Difference between curie temperature and neel temperature Ferrimagnetism
Ferrimagnetism Difference between curie temperature and neel temperature
Difference between curie temperature and neel temperature Reynold’s transport theorem
Reynold’s transport theorem Euler's equation of motion derivation
Euler's equation of motion derivation Anaesthesit
Anaesthesit Dilution principle of measuring body fluids
Dilution principle of measuring body fluids 4/2/1 rule
4/2/1 rule Fluids physics problems and solutions
Fluids physics problems and solutions Fluids
Fluids Nsw health emergency flip chart
Nsw health emergency flip chart Bio fluids
Bio fluids What is rolling friction
What is rolling friction Fluid statics
Fluid statics Monometer equation
Monometer equation What is the upward force that fluids exert on all matter
What is the upward force that fluids exert on all matter Pgage
Pgage