System Planning 2013 Lecture 7 Optimization Appendix A

System Planning 2013 • • • Lecture 7: Optimization Appendix A Contents: – – General about optimization Formulating optimization problems Linear Programming (LP) Mixed Integer Linear Programming (MILP) 1

Optimization – General • Discipline in applied mathematics • Used when: – Want to maximize or minimize something (e. g. profit or cost) under various conditions (e. g. generation capacities, transmission limits) 2

Optimization – General Typical problems • In what sequence should parts be produced on a machine in order to minimize the change-over time? • How can a dress manufacturer lay out its patterns on rolls of cloth to minimize wasted material? • How many elevators should be installed in a new office building to achieve an acceptable expected waiting time? • What is the lowest-cost formula for chicken food which will provide required quantities of necessary minerals and other nutrients? • What is the generation plan for the power plants during the next six hours? 3

Optimization - General The general optimization problem: Defines the feasible set • f(x): • x: • g(x), h(x): • and : objective function optimization variables (vector) constraints (vectors) variabel limits (vector) 4

Optimization – Formulation of optimization problems: 1. Describe the problem in words: • 2. Define symbols • 3. Think through the problem Review the parameters and variables involved Write the problem mathematically • Translate the problem defined in words to mathematics 5

Optimization – Formulation The problem: A manufacturer owns a number of factories. How should the manufacturer ship his goods to the customers? ? 6

Optimization – Formulation 1. The problem in words: How should the merchandise be shipped in order to minimize the transportation costs? The following must be fulfilled: • The factories cannot produce more than their production capacities. • The customers must at least receive their demand 7

Optimization – Formulation 2. • • Define symbols: Index and parameters: m factories, factory i has capacity ai n customers, customer j demand bj units of the commodity The transportation cost from factory i to customer j is cij per unit Variables Let xij, i = 1. . . m, j = 1. . . n denote the number of units of the commodity shipped from factory i to customer j 8

Optimization – Formulation 3. Mathematical formulation: • Objective function Transportation cost: • Constraints Production capacity: Demand: Variable limits: 9

Optimization – Formulation The optimization problem: 10

LP – General Linear Programming problems (LP problems) • Class of optimization problems with linear objective function and constraints • All LP problems can be written as (standard form): 11

LP – General • LP problems will here be explained through examples (similar as in Appendix A) • Will have to look at the following: – – – – – Extreme points Slack variables Non existing solution Not active constraints No finite solution or unbounded problems Degenerated solution Flat optimum Duality Solution methods 12

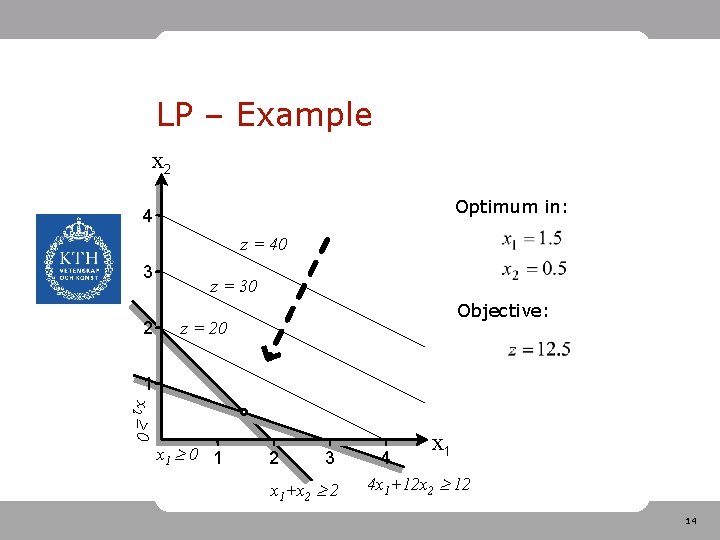
LP – Example • The problem: 13

LP – Example x 2 Optimum in: 4 z = 40 3 2 z = 30 Objective: z = 20 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 x 1 4 4 x 1+12 x 2 12 14

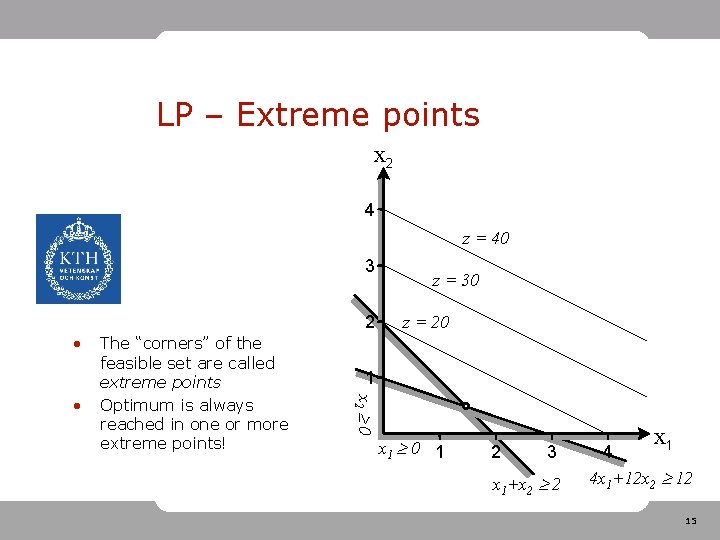
LP – Extreme points x 2 4 z = 40 3 2 • z = 20 1 x 2 0 • The “corners” of the feasible set are called extreme points Optimum is always reached in one or more extreme points! z = 30 x 1 0 1 2 3 x 1+x 2 2 x 1 4 4 x 1+12 x 2 12 15

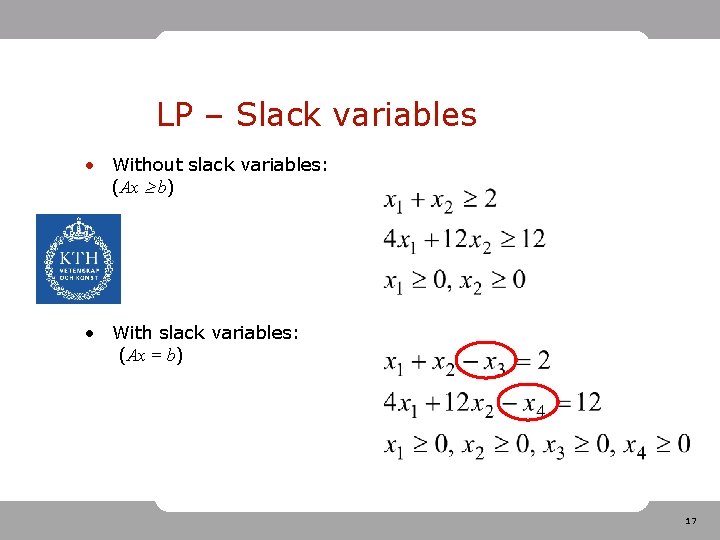
LP – Slack variables • LP problem on standard form: • Introduce slack variables in order to write inequality constraints using equality 16

LP – Slack variables • Without slack variables: (Ax b) • With slack variables: (Ax = b) 17

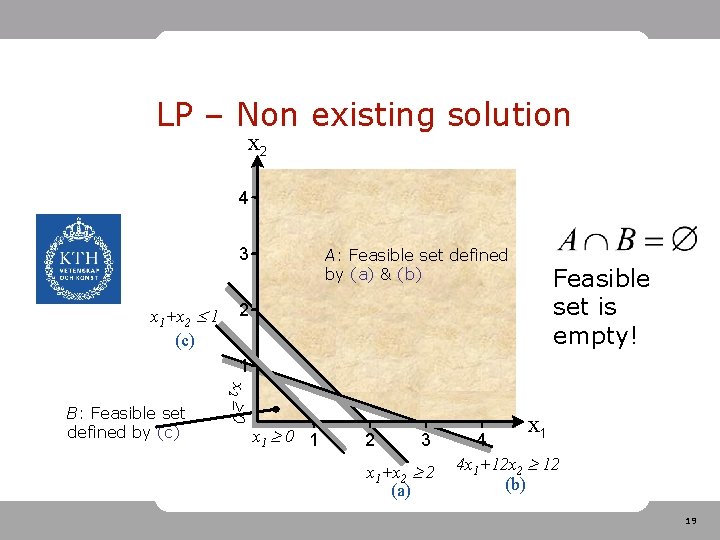
LP – Non existing solution • Can happen that the constraints makes no solution feasible! (Bad formulation of problem) New constraint 18

LP – Non existing solution x 2 4 3 x 1+x 2 1 (c) A: Feasible set defined by (a) & (b) Feasible set is empty! 2 1 x 2 0 B: Feasible set defined by (c) x 1 0 1 2 3 x 1+x 2 2 (a) x 1 4 4 x 1+12 x 2 12 (b) 19

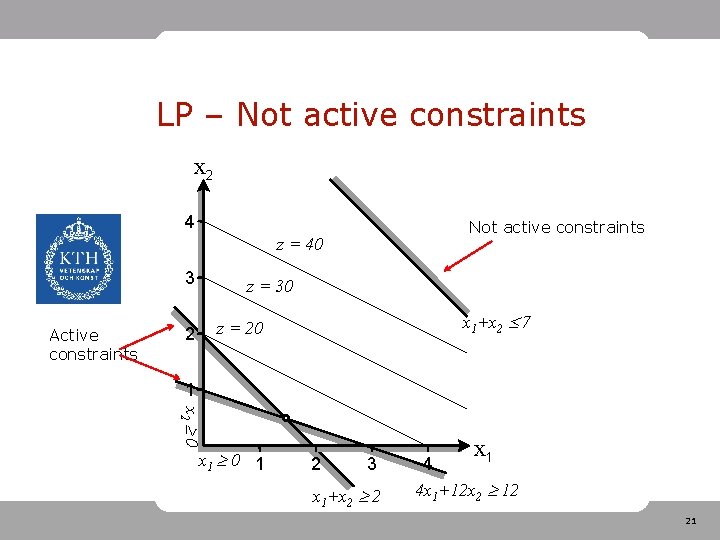
LP – Not active constraints • Some constraints might not be active in optimum. New constraint 20

LP – Not active constraints x 2 4 Not active constraints z = 40 3 Active constraints z = 30 x 1+x 2 7 z = 20 2 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 x 1 4 4 x 1+12 x 2 12 21

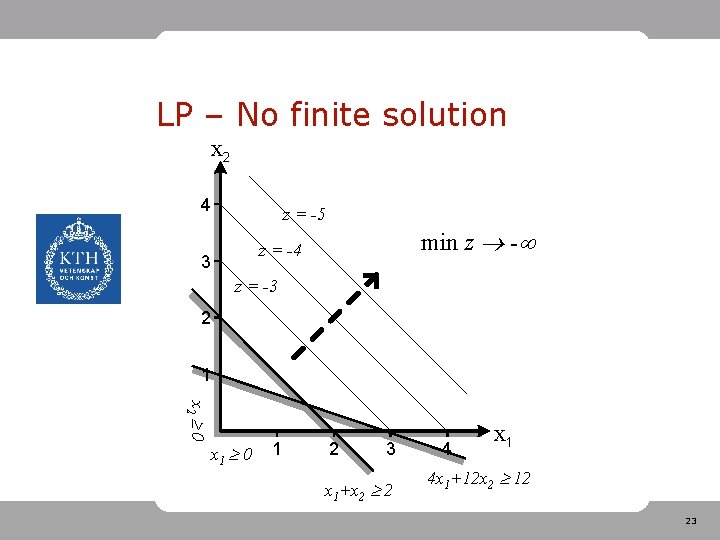
LP – No finite solution • If the constraints don’t limit the objective: | z| New objective function 22

LP – No finite solution x 2 4 z = -5 min z - z = -4 3 z = -3 2 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 4 x 1 4 x 1+12 x 2 12 23

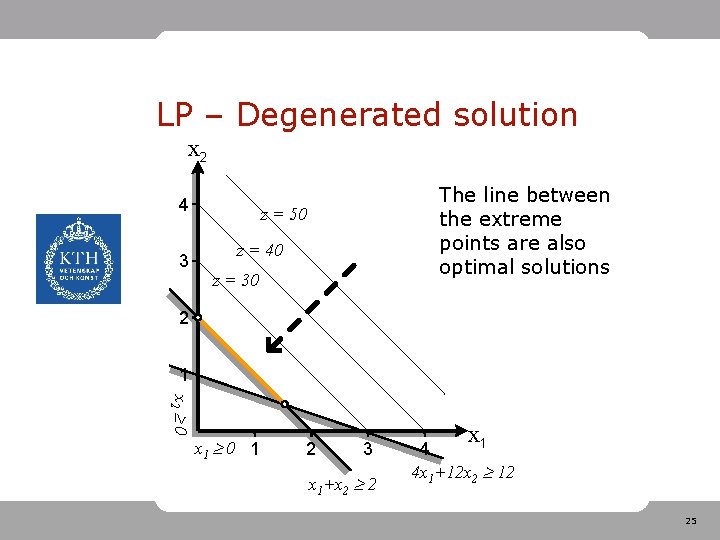
LP – Degenerated solution • More than one extreme point can be optimal. All linear combinations of these points are then also optimal New objective 24

LP – Degenerated solution x 2 4 3 The line between the extreme points are also optimal solutions z = 50 z = 40 z = 30 2 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 x 1 4 4 x 1+12 x 2 12 25

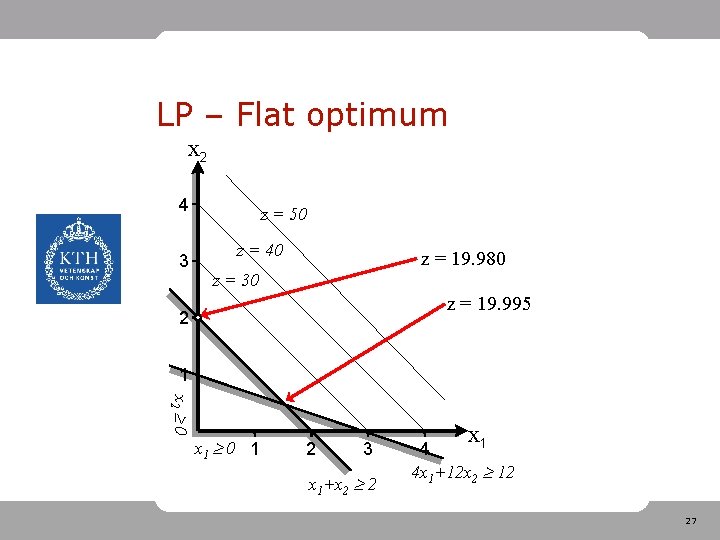
LP – Flat optimum • A number of extreme points can have almost the same objective function value. New objective 26

LP – Flat optimum x 2 4 3 z = 50 z = 40 z = 19. 980 z = 30 z = 19. 995 2 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 x 1 4 4 x 1+12 x 2 12 27

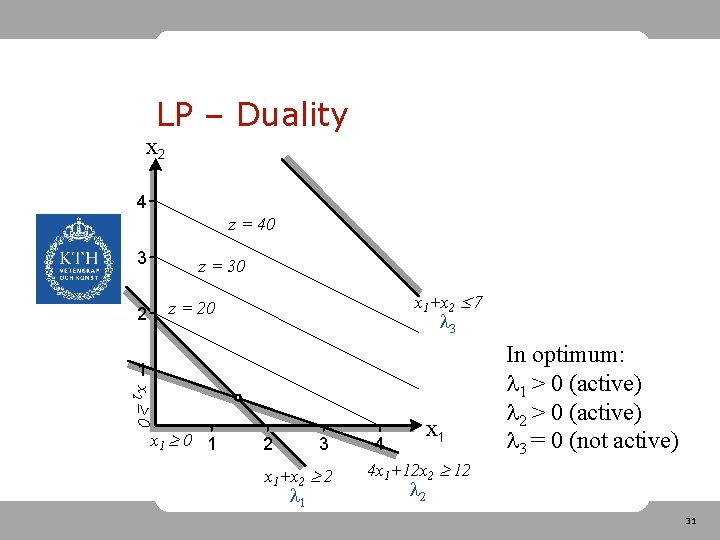
LP – Duality • All LP problems (primal problem) have a corresponding dual problem Primal problem: Dual problem: • are called dual variables 28

LP – Duality Theorem (strong duality): If the primal problem has an optimal solution, then also the dual problem has an optimal solution and the objective values of these solutions are the same. 29

LP – Duality • Q: What does the dual variables describe? • A: Dual variables = Marginal value of the constraint that the dual variable represents, i. e. how the objective function value changes when the right-hand side of the constraint changes One dual variable for each constraint! 30

LP – Duality x 2 4 z = 40 3 z = 30 x 1+x 2 7 z = 20 2 3 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 1 x 1 4 4 x 1+12 x 2 12 In optimum: 1 > 0 (active) 2 > 0 (active) 3 = 0 (not active) 2 31

LP – Duality • Dual variables • Small changes in right-hand side b • Change in objective function value z: z = T b 32

MILP – General Mixed Integer Linear Programming problems (MILP problems) • Class of optimization problems with linear objective function and constraints • Some variables can only take integer values 33

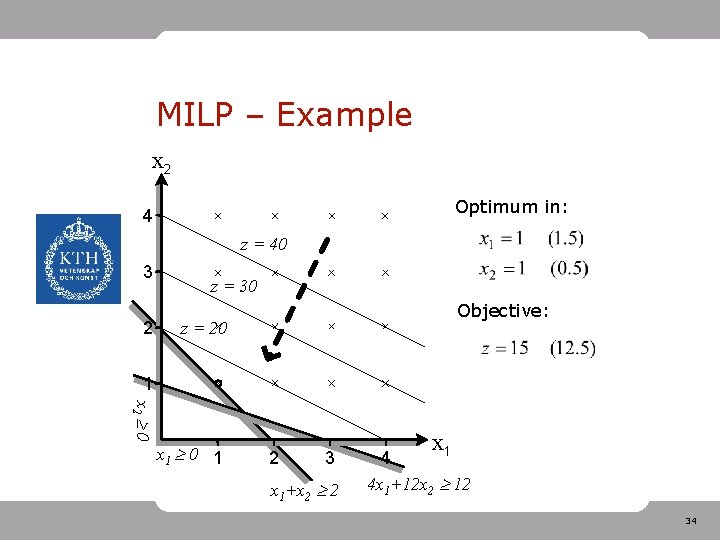
MILP – Example x 2 Optimum in: 4 z = 40 3 2 z = 30 Objective: z = 20 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 x 1 4 4 x 1+12 x 2 12 34

MILP – Solving • Easy to implement integer variables. • Hard to solve the problems. – Execution times can increase exponentially with the number of integer variables • Avoid integer variables if possible! • Special case of integer variables: Binary variables x {0, 1} 35

MILP – Example • • Minimize the cost for buying ”something” Variable, x: Quantity of ”something”, x 0. Not constant cost per unit - cost function. For example: Discount when buying more than a specified quantity: Cost [SEK] x 2 x 1 Split x into two different variables, x 1 and x 2. Observe that x 1≤ xb. Also note that both x 1 and x 2 are 0. xb Number of ”units” 36

MILP – Example Cost [SEK] x 2 x 1 xb Number of ”units” • Cheaper to buy in segment 2 Must force the problem to fill the first segment before entering segment 2. • Can be performed by introducing a binary variable. 37

MILP – Example Cost [SEK] • Let s be an integer variable indicating whether being in segment 1 or 2. x 2 x 1 • Introduce the following constraints: xb s=0 s=1 Number of ”units” where M is an arbitrarely large number. Check if s=0: Check if s=1: 38

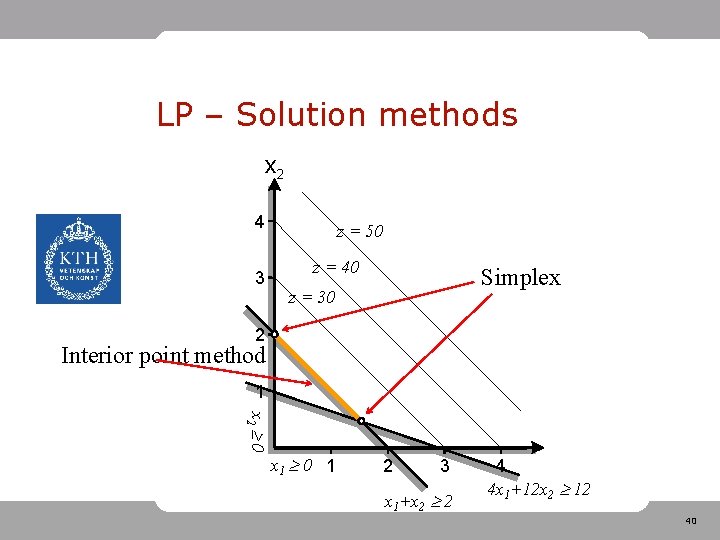
LP – Solution methods • Simplex: Returns optimum in extreme point (also when degenerated solution) • Interior point methods: If degenerated solution: Returns solution between two extreme points 39

LP – Solution methods x 2 4 3 z = 50 z = 40 Simplex z = 30 2 Interior point method 1 x 2 0 x 1 0 1 2 3 x 1+x 2 2 4 4 x 1+12 x 2 12 40

PROBLEM 11 - Solutions to LP problems Assume that readymade software is used to solve an LP problem. In which of the following cases do you get an optimal solution to the LP problem and in which cases do you have to reformulate the problem (or correct an error in the code). a) The problem has no feasible solution. b) The problem is degenerated. c) The problem does not have a finite solution. 41