Symmetry of Properties q Various properties Mechanical Electrical

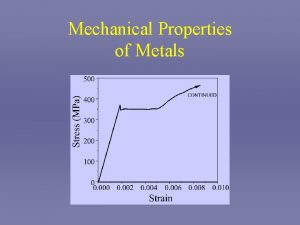
Symmetry of Properties q Various properties: Mechanical, Electrical, Magnetic, Thermal, etc. q Tensorial nature of properties. q Symmetry imposed restraints. Part of ü Neumann Principle ü Curie Principle ü Illustration of principles using Thermal, Electrical and Elastic properties MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: anandh@iitk. ac. in, URL: home. iitk. ac. in/~anandh http: //home. iitk. ac. in/~anandh/E-book. htm Advanced Reading Physical Properties of Crystals: Their Representation by Tensors and Matrices. J. F. Nye Clarendon Press, Oxford, 1985. Properties of Materials: Anisotropy, Symmetry, Structure. Robert E Newnham Oxford University Press, Oxford, 2005.

Overview of Properties For now we concern ourselves with properties of crystals q For every stimulus there is a natural response. E. g. : when electric field is applied to a dielectric material it can lead to electric polarization, when stresses develop inside a material, it can lead to strains, application of magnetic field can lead to magnetization. q In addition there can be cross-coupling terms, i. e. one kind of stimulus can lead to response*, which is not naturally associated with it. E. g. : application of pressure[1] can lead to electric polarization (piezoelectricity), presence of temperature difference can cause electrical potential difference (pyroelectricity), the electrical resistance is altered in the presence of a magnetic field (magnetoresistance). q A stimulus can be connected to a response via a material property. E. g. : M = . H, = E. , P = p. T. The material property has to be measured via experiments (or computed from more fundamental properties). q In reality the stimulus and response are tensors** (of various orders) and hence the material property is also a tensor of some rank (i. e. many values may be required to describe the property). The equations (as above) in tensorial form become: Mi = ij. Hj, ij = Eijkl kl, Pi = pi T. [1] The correct phraseology should be: “application of forces/constraints”. The application of forces can lead to stresses in the material, which can further cause electric polarization. Actually, pressure is a parameter better used in the context of fluids (and stress, a tensor, a better quantity for solids). The hydrostatic component of stress is “like the pressure”. * There could be more than one response. ** More on this soon.

Classification of material properties Overview of Properties (Cotd. ) Polar tensors (rank 0 -4) Axial tensors (rank 0 -4) Material Properties Transport properties § Relate flow to a gradient Properties with hysterisis § Involve domain wall motion Examples of 1 st to 4 th ranked tensor properties The number of subscripts denotes the order of the tensor

“Cross-coupling” effects & Heckmann diagrams q A stimulus can lead to effects, which are not naturally associated with it. E. g. stress can lead to electric polarization (piezoelectricity). q The “natural” effects and “cross-coupling” effects can be pictorially represented using Heckmann diagrams (as below).

Scalar, Vector and Tensor Quantities q To describe a property at a point inside the material we may require to specify just: a number (magnitude of that property like temperature or density), a magnitude and direction (i. e. 3 numbers in 3 D like for electric field or pyroelectric coefficient) or even more numbers. The number of values required is given by 3 n in 3 D (2 n in 2 D); where ‘n’ is called the rank of the tensor. q To understand why tensors are required let us consider a force ‘F’ (with a F) applied along the x-axis and ask the question*: “what will happen to the body? ”. q Clearly the information available is insufficient to answer unequivocally. If the forces are applied as in Fig. 1 b the body will elongate, while if applied as in Fig. 1 c the body will shear. q Hence, we need to specify the plane on which the force is acting. In case in Fig. 1 b the +F force is acting on the +x-plane along the +x direction this is written as Fxx. In Fig. 1 c the force +F is acting along the +y-plane along the +x direction written as Fyx. q This implies (in this example of mechanical deformation) two directions are required to specify the force (and hence determine its effect): (i) the direction of the plane normal and (ii) the direction of the force. q A combination of these forces Fxx & Fxy could also be acting on the body. F Fig. 1 a F Fig. 1 b F Fxx Note. For tension/compression: +F on +x face is positive and similarly, F force on x plane is also positive. For shear: shear causing clockwise rotation is positive. * For now we will assume that other forces are present to give us force and moment balance (i. e. equilibrium condition). Also note that force (F) is a vector and we are trying to understand its effect as a prelude to tensors. Fig. 1 c F Fyx

Q&A Give examples of axial and polar vectors. q Polar vectors: Force, Electric field, Polarization. q Axial vectors: Mechanical moment, Angular momentum, Curl of a polar vector. Some basic points. . . q A scalar does not require a coordinate system to define and hence is independent of the coordinate axes chosen. We require just one number at each point for a scalar. q A vector can be represented by its components along a set of coordinate axes. We require three numbers in 3 D at each point to specify a vector. A change in the coordinate axes system (change in the angle between the basis vectors, translation/rotation of the basis vectors) will change the components along the axes; but, will the vector itself will remain unchanged. q The transformation of a vector (rotation, inversion, mirror, etc. ) can be carried out using a transformation matrix. q A second rank tensor can also can be represented by its components along a set of coordinate axes. It can be visualized as a combination of two directions. We require nine numbers in 3 D at each point to specify a second rank tensor. A change in the coordinate axes system will change the components along the axes; but, will the tensor itself will remain unchanged. q The transformation of a second rank tensor can be carried out using two transformation We will repeat some of these concepts soon. matrices.

Tensors of various ranks q Tensors can be used to describe: (i) fields (field tensors) or (ii) properties (property tensors). q These tensors can belong to various ranks: zeroth rank, first rank, second rank, etc. § E. g. Temperature field is a scalar field, where each point in space is described by one number the ‘T’ at that point (T(x, y, z)). Scalar fields are tensor fields of rank-0. On the other hand some fields require more numbers to be specified at each point in space. § Electric field (polar vector) and Magnetic field (axial vector) require three numbers (in 3 D) to be specified at each point. These 3 numbers are the components along the coordinate axes and give the direction and magnitude of the vector. Such a field is a vector field. Vectors are tensors of rank-1. § Some other fields require more numbers to be specified. E. g. to describe the state of stress at a point, we need 9 numbers (in 3 D) in general (stress being a symmetric tensor we actually need only 6 numbers). Stress is a tensor of rank-2. Q&A q Why do we need coordinate transformations? We have already seen (Matrix representation of symmetry operators) that symmetry operators can be written as transformation matrices; which involve operations like rotation (about a crystallographic axis), inversion (about an inversion centre usually the centre of the unit cell) and mirror (about a plane usually passing through lattice points are exactly between lattice points). * Note: only one number needed at each point. If there is a to point variation of temperature a set of T have to be specified for each (x, y, z) which gives rise to the temperature field.

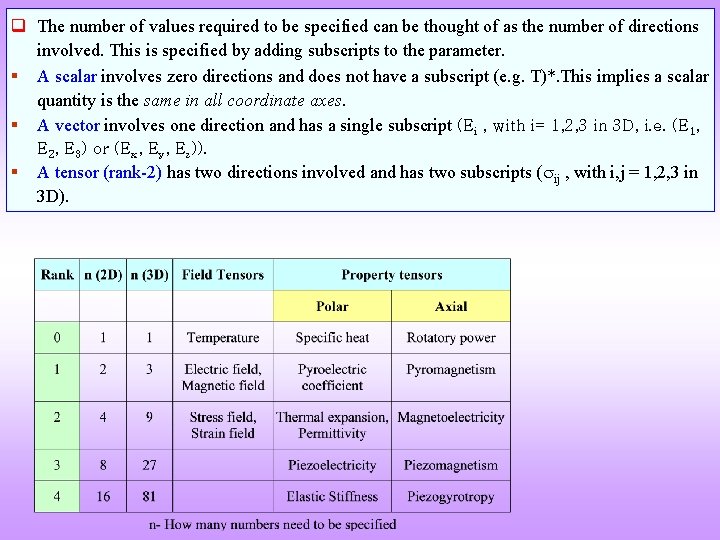
q The number of values required to be specified can be thought of as the number of directions involved. This is specified by adding subscripts to the parameter. § A scalar involves zero directions and does not have a subscript (e. g. T)*. This implies a scalar quantity is the same in all coordinate axes. § A vector involves one direction and has a single subscript (Ei , with i= 1, 2, 3 in 3 D, i. e. (E 1, E 2, E 3) or (Ex, Ey, Ez)). § A tensor (rank-2) has two directions involved and has two subscripts ( ij , with i, j = 1, 2, 3 in 3 D).

Vectors and their transformations q The direction and magnitude of a vector (vector is a first rank tensor) is same in any coordinate system. Let us consider a vector P in (x, y) coordinate axes with intercepts (Px, Py). Let us consider rotation of axes by an angle (using z-axis) as in the figure below. q The new intercepts along the coordinate axes (Px’ , Py’) can be related to the old ones (x, y) by a transformation matrix (aij). Needless to say the magnitude and direction of the vector remains unchanged during the rotation of the coordinate system only the intercepts (x, y) along the coordinate axes change. The aij are nothing but the direction cosines between the new and the old axes. q For a certain specific orientation ( = 0) the component along y-axis (or for that matter the x-axis) will be zero. These equations can be written as: Using Einstein’s summation convention Transformation Matrix

In this equation ‘i’ is free index and ‘j’ is the dummy index (over which the sum is performed) i=1, 2 & j = 1, 2 (here the ‘=‘ means ‘takes values of’ ). ‘x’, ‘y’ can also b replaced with indices ‘ 1’, ‘ 2’. In 3 D the aij will be a 3× 3 matrix and the equation using direction cosines (as in table below) can be written as: The condensed equation (in 3 D) still remains the same except that i = 1, 2, 3 & j = 1, 2, 3 Direction cosines (3 D) The reverse transformation Sometimes we need to go from the old to the new coordinate system*. In this case the equations turn out to be: Note the position of the dummy index now (in aji) Q&A Which is the vector we are transforming here? q The vector we have considered could be a field vector, like a stimulus or a response (E or P); or could be a property vector like pyroelectric coefficient (p). * Hey! Can’t I just call the new old and the old new?

Transformation of Tensors q As mentioned before there are two kinds of tensors (here we are keeping our focus on 2 nd and higher rank tensors): (i) field tensors and (ii) property tensors. Many material/physical properties have a tensorial nature (i. e. are tensors). q The effect of symmetry on physical properties can be determined by how the tensor transforms under a symmetry operation. q The magnitude of a property in any arbitrary direction can be evaluated by transforming the tensor. q As expected, under the action of a symmetry operator of a crystal the Tensor properties do not change. q Scalar such as Temperature is same in all coordinates. So, if the temperature is ‘T’ at a point in space, it is still same whatever coordinates we choose. q We have already seen how vectors transform; now let us see how 2 nd rank tensors transform (due to coordinate transformation). Let us consider a vector (pi) related to another vector (qj) via a tensor (Tij). [p & q could be fields as we shall see later]. Let p, q be polar vectors for now. In matrix form Using Einstein summation convention ‘i’ is free index and ‘j’ is the dummy index (over which the sum is performed) Continued…

We have used only two concepts here: (i) vector transformation from one coordinate axes to another. (ii) Stimulus (qj) leading to response (pi) via a property tensor (Tij) We have (1) (2) The vector pi (or pk) transforms to the new coordinate system as: In terms of the alternate indices (1) can be written as: (3) The vector qi (or qk) transforms to the old coordinate system from new as: (4) Putting together equations (2, 3, 4): That is: Now this is nothing but the relation between p and q in the new coordinate system (the ‘’’ system). This implies that the quantity in the brackets must be Tij’ The tensor in the primed coordinate system. This is the transformation of a second order property tensor from ‘old’ to ‘new’ coordinate axes. For the transformation of a vector we had one matrix here we have two. ‘i, j’ are free indices and ‘k, l’ are dummy indices (over which the sum is performed)

Alternate Matrix method for Tensor Transformation We have noted that we can transform 2 nd rank tensors using the relation A alternate matrix form of this equation is also very useful, which can be derived as below. The relations we have already seen are: Vectors from old to new coordinate system One vector to another in old coordinate system § For a orthogonal matrix the transpose is the inverse: (a)T = (a) 1 One vector to another in new coordinate system Next we substitute one by one these relations to identify [T’] Don’t get confused by the two Ts (one is for Tensor and other for transpose) Noting that: We get:

Notes on transformation matrices § The new set of axes is related to the old set by three direction cosines (3 nos. ). This implies that not all the 9 terms in the transformation matrices (aij) are independent and only 3 are independent. This implies that there must be 6 relations between the (aij). § As each row in the (aij) matrix represents a direction of a vector with respect to 3 orthogonal axes (i. e as direction cosines), we have three relations of the type: Cos 2α+ Cos 2β+ Cos 2 = 1. § As any row represents one of the orthogonal directions, product of any two rows is zero. Determinant of the transformation matrices For a transformation that leaves the handedness of +1 an axis unchanged (e. g. a rotation) 1 For a transformation that changes the handedness of an axis (e. g. a inversion or mirror) § The determinant of any orthogonal matrix is either +1 or − 1. § All the matrices associated with symmetry operations (rotations, inversion, mirror) are orthogonal. § The value of the determinant is 1, as these transformations should not change the magnitude of the vector.

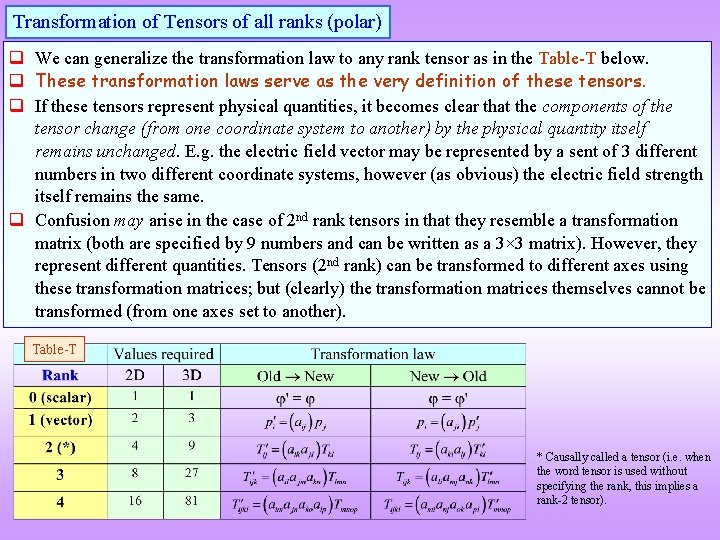
Transformation of Tensors of all ranks (polar) q We can generalize the transformation law to any rank tensor as in the Table-T below. q These transformation laws serve as the very definition of these tensors. q If these tensors represent physical quantities, it becomes clear that the components of the tensor change (from one coordinate system to another) by the physical quantity itself remains unchanged. E. g. the electric field vector may be represented by a sent of 3 different numbers in two different coordinate systems, however (as obvious) the electric field strength itself remains the same. q Confusion may arise in the case of 2 nd rank tensors in that they resemble a transformation matrix (both are specified by 9 numbers and can be written as a 3× 3 matrix). However, they represent different quantities. Tensors (2 nd rank) can be transformed to different axes using these transformation matrices; but (clearly) the transformation matrices themselves cannot be transformed (from one axes set to another). Table-T * Causally called a tensor (i. e. when the word tensor is used without specifying the rank, this implies a rank-2 tensor).

Polar and axial tensor properties of rank 0, 1, 2, 3 and 4

Symmetry of property & symmetry of a crystal q In a amorphous material there is no symmetry at the atomic level. This implies that there is no preferred direction in a glass i. e. glasses are isotropic* (any property measured along any direction will have the same value). q On the other hand crystals can** be anisotropic (i. e. properties can be direction dependent). q It is perhaps obvious that the symmetry of a property should have$ the symmetry of the crystal ($as we shall see soon this is actually ‘at least the symmetry of the crystal’). E. g. for a crystal with 4 mm symmetry a property measured along +x will have the same value as that along +y. E. g. if a field is applied along +x and the current is measured along +x (Jx) this will be equal to the current measured along +y (if field is applied along +y). q We expect from 4 -fold symmetry and inversion centre (mirrors) present: J+x = J+y = J x = J y ** Will it really be anisotropic or not will depend on other factors (including the rank of the tensor and the symmetry of the crystal) and will be considered later. * It is important to note that glasses with no symmetry at the atomic level have the highest symmetry with respect to properties!

Neumann principle* q We have already noted that the symmetry of a property should be equal to that of the crystal. q However, a property may have higher symmetry. So the correct statement is: the symmetry of a property can be equal to that or greater than that of the crystal. Other statements of the Neumann principle. q Symmetry elements of a physical property of a crystal must include all the symmetry elements of its point group (all its rotational axes, mirror planes, etc. ). Examples of a property having a higher symmetry (than the point group symmetry). We will understand the details soon. q All properties that can be represented by tensors of rank up to 2 are isotropic for cubic crystals. E. g. electrical conductivity of cubic crystals is isotropic. * A closely related principle is the Curie Principle (Curie Principle).

How to use Symmetry & Neumann principle to determine the number of independent constants in a property tensor? 1) Start with the property tensor (say in matrix form). 2) Reduce the number of independent components based on any constrains out the symmetry of the crystal (e. g. symmetry of the stimulus, response, energy considerations, etc. ). List out the independent components at the end of all these considerations. 3) Use the appropriate transformation law based on the rank of the tensor (Table-T). Use alternate matrix based transformation rules where applicable (and easier). 4) Apply the appropriate transformation matrices corresponding to the symmetry operators of the crystal (only the bare minimum symmetry operators need to be used (the generator matrices)). In some cases where direct application of transformation principles are possible, the same can be used (e. g. a 3 -fold along [111] in cubic crystals takes: x y, y z & z x). 5) After the application of each transformation, apply Neumann’s principle. I. e. the transformed components must be equal to the original components. Based on this determine the ‘equal’ components of the property tensor and the zero components. These steps will become clear once we take up some actual solved examples in this chapter.

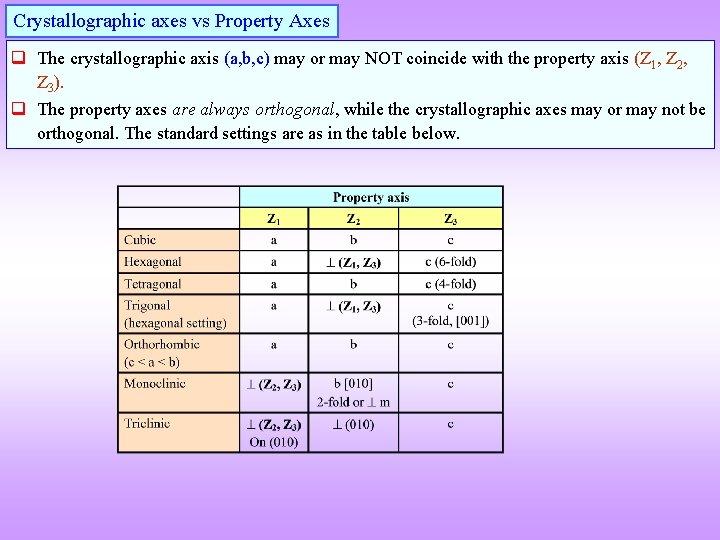
How to understand anisotropy? q Let us start with a toy model to ‘visualize’ anisotropy in crystals. If the glass ball is pulled as shown then it will not move along the direction of pull, but will move along the direction as marked. I. e. even if the stimulus is along ‘P’, the response is along ‘A’. P Tension Shear A q We can think of two alternate ways to understand anisotropy: The direction of the response is different from the direction of the stimulus (if electric field is applied along ‘S’ direction of a crystal the current may flow along ‘R’). The response may involve other terms than the ‘natural’ expectation due to the stimulus (e. g. if a crystal is stretched along ‘F’, it may shear in addition to being elongated).

Funda Check What can happen if we pull, bend or twist an anisotropic crystal? q If we pull the crystal it may elongate and shear. q If we bend the crystal using pure bending moments, it may bend and twist. q If we twist the crystal using pure torsional moments, it may twist and bend. q The words in red are not the natural responses to the applied load. q In an isotropic material only the green responses will exist.

How is that a block of Copper is isotropic (say with respect to its elastic properties)? Origin of isotropy at the level of the microstructure and partial anisotropy in crystalline materials q At the level of the crystal structure (in a single crystal), a given property may be isotropic due to Neumann’s principle (e. g. cubic crystals like Na. Cl are optically isotropic). However, isotropy may also arise due to spatial averaging of properties at the level of the microstructure. q A single crystal of Cu will be anisotropic with respect to its elastic properties (we will see later that 3 independent elastic constants are required: E 11, E 12, E 44). q However, a block of Cu is polycrystalline with multiple grains oriented randomly: thus there is no preferred direction for the Cu block and its elastic properties are isotropic* (we require only two independent moduli: E (Young’s modulus) and (Poisson’s ratio) to describe the its elastic response). q In a wire of Cu, the grains may not be oriented randomly and such a material is said to possess crystallographic texture. I. e. in a textured material there is (some degree of) preferential orientation of grains. Texture can develop during rolling, extrusion, wiredrawing, thin film growth, etc. q In textured materials, the anisotropy present at the level of the single crystal is partially recovered. Atomic structure level Single crystals Origin of Isotropy Due to Neumann’s principle * Assuming that the block has many grains and hence all orientations are represented. Microstructure level Also for textured materials

Stimulus and Response q q q We can apply various kinds of stimuli on a material (like Force, Electric Field, Magnetic Field, Temperature difference, etc. ). These fields may give rise to natural responses (like elongation, electric current or polarization, magnetization, heat flow, etc. ). However, we may also get responses which are usually associated with other kinds of stimuli. E. g. the application of pressure may lead to the polarization of the crystal (Piezo-electric effect) or the application of a magnetic field may lead to strain in the material (magnetostriction). A material/physical property connects the stimulus to the response. The stimulus response plot may be linear, non-linear or may even show hysteresis. The physical property connecting a stimulus of rank-p to a response of rank-q will be of rank -(p+q). E. g. in the table below stimulus jk is of rank-2, response Pi is of rank-1 and the property dijk is of rank-3. (As stated before)

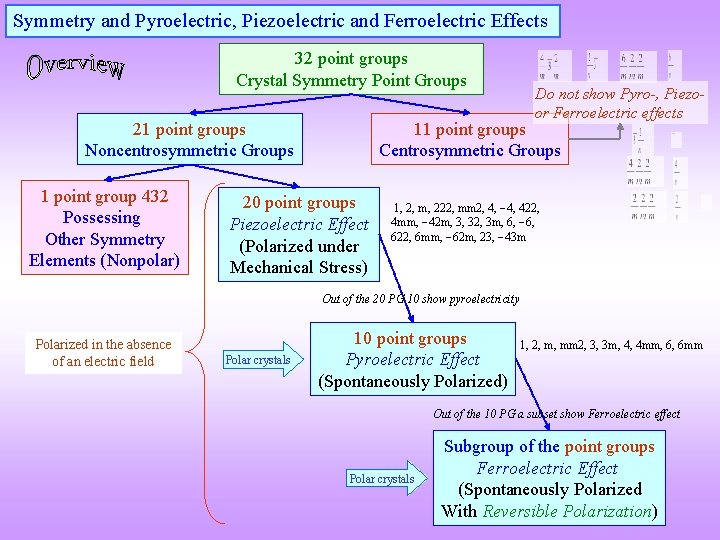
Crystallographic axes vs Property Axes q The crystallographic axis (a, b, c) may or may NOT coincide with the property axis (Z 1, Z 2, Z 3). q The property axes are always orthogonal, while the crystallographic axes may or may not be orthogonal. The standard settings are as in the table below.

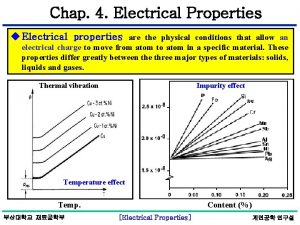
Electrical Properties q The response of an electric field on a material can be: (i) motion of charges (electrons or ions), (ii) polarization. In metals electrons flow on the application of an electric field, while in materials like solid electrolytes ions carry the current. Materials which lack free charges are called di-electrics (should have been called dia-electrics, which would have made it consistent with dia-magnetics). In dielectrics, the internal field weakly opposes the external field (like in diamagnetic materials the internal magnetic field weakly opposes the external field). q In some crystals the centre of mass of the positive charges does not coincide with the centre of mass of negative charges, leading to a net electric dipole. These crystals are spontaneously polarized in the absence of an external field polar materials. Such crystals lack a centre of symmetry (inversion centre). q In piezoelectric, pyroelectric and ferroelectric materials the polarization is spontaneous, i. e. it exists in the absence of an external electric field.

q Polar materials come in two types: § (i) those in which the reversal in field direction can reverse the direction of spontaneous polarization (called Ferro-electrics) and § (ii) those in which this does not happen. Ferroelectric materials show a hysteresis in the electric field-polarization plot. In general, materials which show hysteresis in stimulus-response plots are called Ferroics. q In certain crystals pressure (mechanical stress) can lead polarization (or change in polarization if the crystal already has spontaneous polarization). These materials are termed as Piezoelectric. It is also possible that electric field can lead to mechanical strain in the material this is termed as Inverse Piezoelectric effect. Both of these effects are “crosscoupling terms” as we had seen when we discussed Hartmann diagrams. q In the next slide we consider the effect of symmetry on piezo-, pyro- and ferro- electric properties. We will see that out of the 32 point groups only 20 have the potential to show piezoelectric properties. The point groups with centre of symmetry (11 nos. ) cannot show piezoelectric effect, as centre of mass of the +ve and ve ions will coincide in these cases. Only 10 of these 20 show the pyroelectric effect. A subset of these 10 point groups show the ferroelectric effect. q In Ferroelectric materials some ions may be displaced by ~0. 1Å.

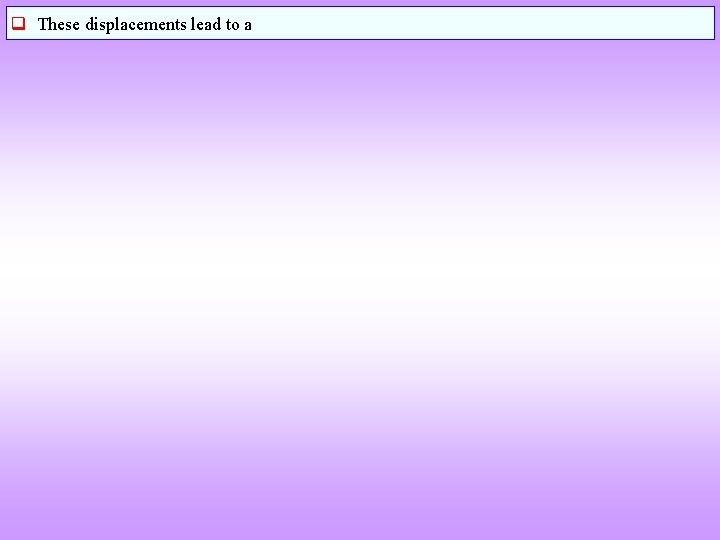
Symmetry and Pyroelectric, Piezoelectric and Ferroelectric Effects 32 point groups Crystal Symmetry Point Groups 21 point groups Noncentrosymmetric Groups 1 point group 432 Possessing Other Symmetry Elements (Nonpolar) Do not show Pyro-, Piezoor Ferroelectric effects 11 point groups Centrosymmetric Groups 20 point groups Piezoelectric Effect (Polarized under Mechanical Stress) 1, 2, m, 222, mm 2, 4, 422, 4 mm, 42 m, 3, 32, 3 m, 6, 622, 6 mm, 62 m, 23, 43 m Out of the 20 PG 10 show pyroelectricity Polarized in the absence of an electric field Polar crystals 10 point groups Pyroelectric Effect (Spontaneously Polarized) 1, 2, m, mm 2, 3, 3 m, 4, 4 mm, 6, 6 mm Out of the 10 PG a subset show Ferroelectric effect Polar crystals Subgroup of the point groups Ferroelectric Effect (Spontaneously Polarized With Reversible Polarization)

q These displacements lead to a

Pyroelectricity q On heating/cooling in some materials (like tourmaline*, gallium nitride (Ga. N) based materials, caesium nitrate (Cs. NO 3), Lithium tantalate (Li. Ta. O 3, Li. Nb. O 3)) voltage develops, this phenomenon is called pyroelectricity. On heating/cooling charge develops on the opposite faces of crystals lacking centre of inversion. q Heating leads to shift in atomic positions so as to lead to a voltage. q As temperature change (stimulus) does NOT have a directionality, the response (polarization) must correspond to the symmetry of the crystal. q All pyroelectric materials are also piezoelectric, but the vice-versa is not true. q The temperature change ( T) is related to the polarization (P) by: § Pi → polarization vector [C/m 2] § pi → pyro-electric coefficient (polar first rank tensor/vector property) [C/m 2/K] § Pi is a polar vector, which transforms as: * Common black tourmaline has a nominal formula Na. Fe 2+3 Al 6 Si 6 O 18(BO 3)3(OH)

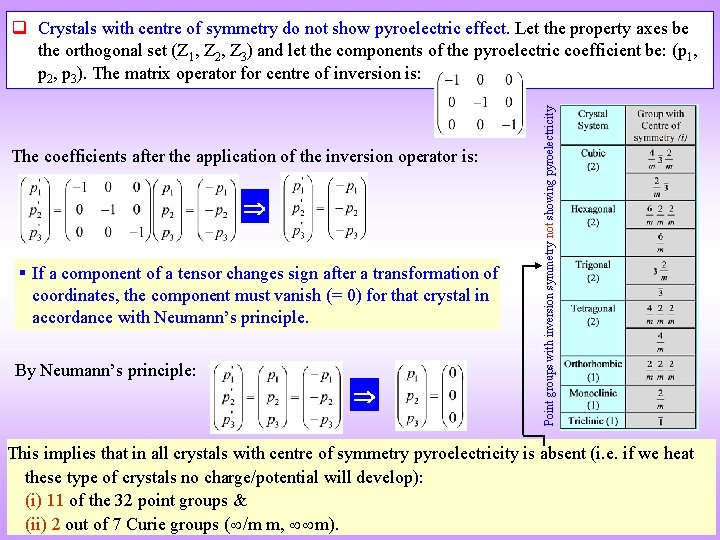
The coefficients after the application of the inversion operator is: § If a component of a tensor changes sign after a transformation of coordinates, the component must vanish (= 0) for that crystal in accordance with Neumann’s principle. By Neumann’s principle: Point groups with inversion symmetry not showing pyroelectricity q Crystals with centre of symmetry do not show pyroelectric effect. Let the property axes be the orthogonal set (Z 1, Z 2, Z 3) and let the components of the pyroelectric coefficient be: (p 1, p 2, p 3). The matrix operator for centre of inversion is: This implies that in all crystals with centre of symmetry pyroelectricity is absent (i. e. if we heat these type of crystals no charge/potential will develop): (i) 11 of the 32 point groups & (ii) 2 out of 7 Curie groups ( /m m, m).

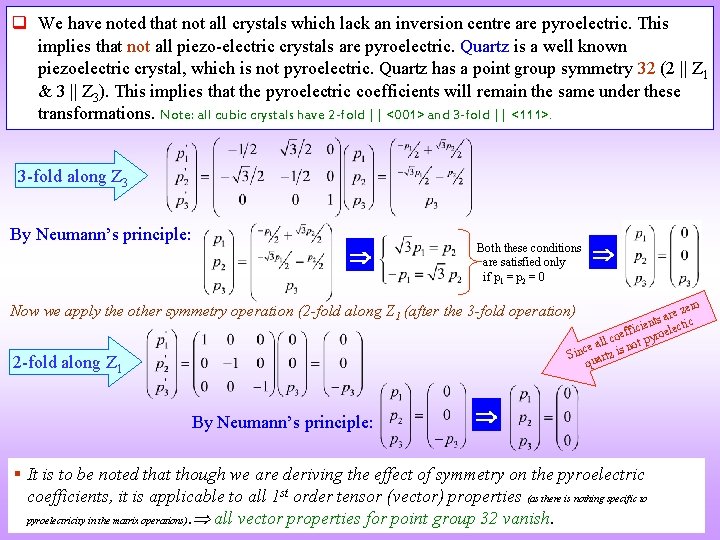
q We have noted that not all crystals which lack an inversion centre are pyroelectric. This implies that not all piezo-electric crystals are pyroelectric. Quartz is a well known piezoelectric crystal, which is not pyroelectric. Quartz has a point group symmetry 32 (2 || Z 1 & 3 || Z 3). This implies that the pyroelectric coefficients will remain the same under these transformations. Note: all cubic crystals have 2 -fold || <001> and 3 -fold || <111>. 3 -fold along Z 3 By Neumann’s principle: Both these conditions are satisfied only if p 1 = p 2 = 0 ero re z a s c nt icie oelecti f f e r o y all c s not p e c i n Si rtz qua Now we apply the other symmetry operation (2 -fold along Z 1 (after the 3 -fold operation) 2 -fold along Z 1 By Neumann’s principle: § It is to be noted that though we are deriving the effect of symmetry on the pyroelectric coefficients, it is applicable to all 1 st order tensor (vector) properties (as there is nothing specific to pyroelectricity in the matrix operations). all vector properties for point group 32 vanish.

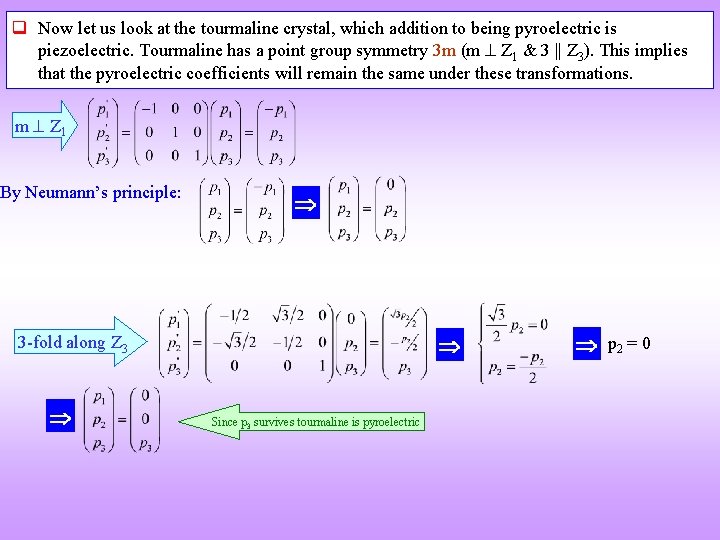
q Now let us look at the tourmaline crystal, which addition to being pyroelectric is piezoelectric. Tourmaline has a point group symmetry 3 m (m Z 1 & 3 || Z 3). This implies that the pyroelectric coefficients will remain the same under these transformations. m Z 1 By Neumann’s principle: 3 -fold along Z 3 Since p 3 survives tourmaline is pyroelectric p 2 = 0

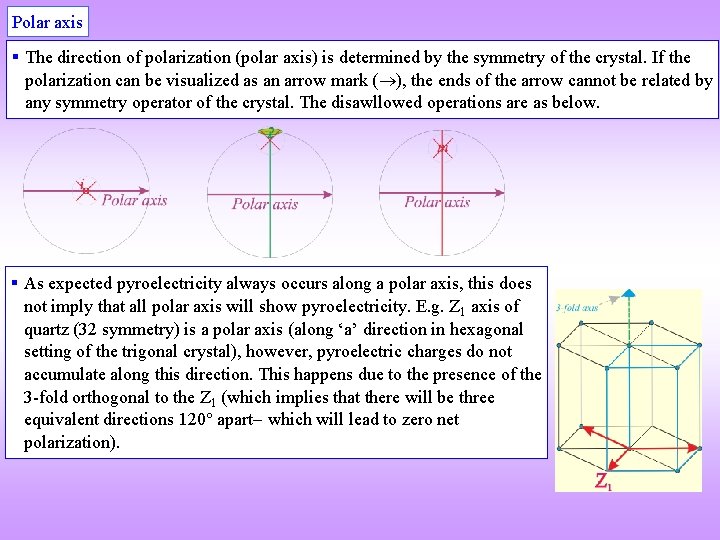
Polar axis § The direction of polarization (polar axis) is determined by the symmetry of the crystal. If the polarization can be visualized as an arrow mark ( ), the ends of the arrow cannot be related by any symmetry operator of the crystal. The disawllowed operations are as below. § As expected pyroelectricity always occurs along a polar axis, this does not imply that all polar axis will show pyroelectricity. E. g. Z 1 axis of quartz (32 symmetry) is a polar axis (along ‘a’ direction in hexagonal setting of the trigonal crystal), however, pyroelectric charges do not accumulate along this direction. This happens due to the presence of the 3 -fold orthogonal to the Z 1 (which implies that there will be three equivalent directions 120 apart which will lead to zero net polarization).

How to locate the Polar axis? § If vectors are drawn from the origin to each of the equivalent points and the resultant obtained, this will be along the polar direction. Examples are shown for point groups m and 2. q If the vectoral sum leads to a zero resultant then there will be no net polarization and hence no polar direction. E. g. for the point group 2/m.

Pyroelectricity in cubic materials q All cubic crystals have 2 -fold || <001> and 3 -fold || <111>. 3 -fold along <111> will take x y, y z & z x. 3 -fold along [111] By Neumann’s principle: Now we apply the other symmetry operation (2 -fold along Z 1 (after the 3 -fold operation) 2 -fold along Z 1 By Neumann’s principle: § It is to be noted that though we are deriving the effect of symmetry on the pyroelectric coefficients, it is applicable to all 1 st order tensor (vector) properties (as there is nothing specific to pyroelectricity in the matrix operations). In cubic crystals first rank tensor properties vanish.

Pyroelectricity in textured materials q Suppose we are not considering a single crystal but a material with texture with m symmetry (a strong electric field along Z 3, which aligns domains parallel to Z 3). Will pyrolectricity survive in the textured material? || Z 3 By Neumann’s principle: If equality in row-1 and row -2 are to be applicable for all values m Z 1 Since p 3 survives the textured material with m symmetry is pyroelectric

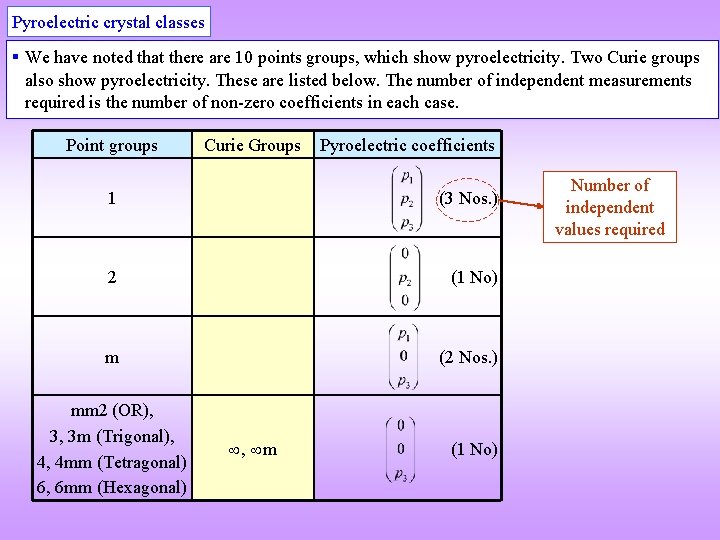
Pyroelectric crystal classes § We have noted that there are 10 points groups, which show pyroelectricity. Two Curie groups also show pyroelectricity. These are listed below. The number of independent measurements required is the number of non-zero coefficients in each case. Point groups Curie Groups Pyroelectric coefficients 1 (3 Nos. ) 2 (1 No) m (2 Nos. ) mm 2 (OR), 3, 3 m (Trigonal), 4, 4 mm (Tetragonal) 6, 6 mm (Hexagonal) , m (1 No) Number of independent values required

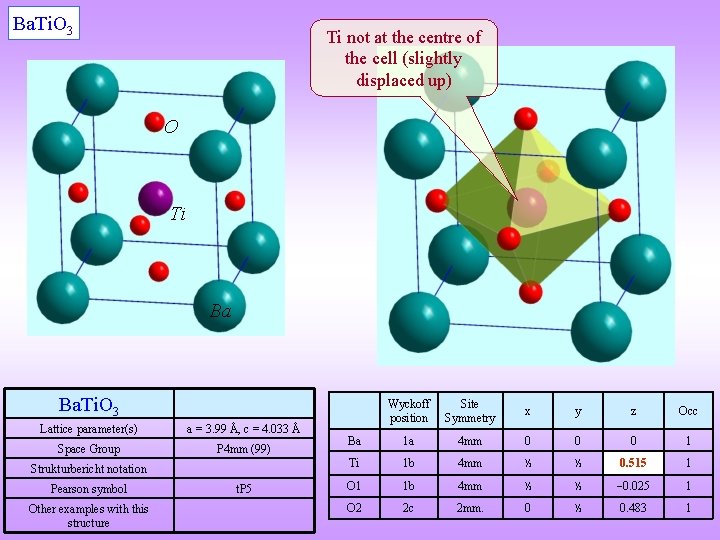
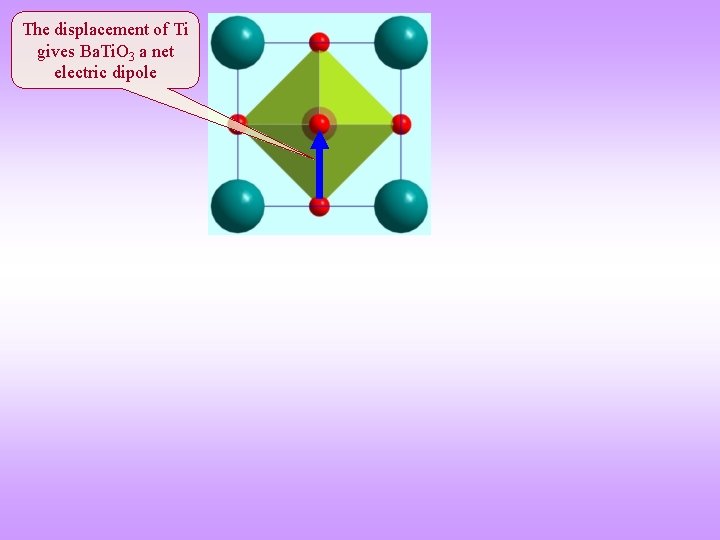
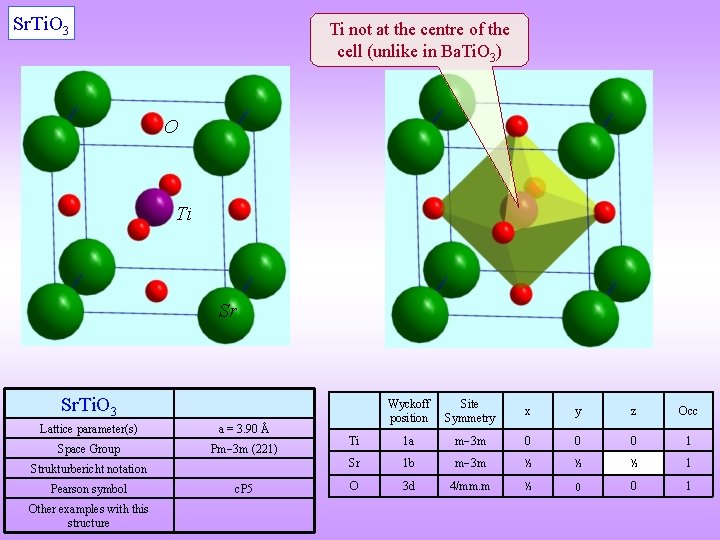
Ferroelectricity With special reference to Perovskites q Ba. Ti. O 3 (a model material w. r. t to ferroelectricity) has a cubic structure with centre of symmetry above 120 C and hence has no permanent dipole moment. Below 120 C the crystal structure is tetragonal, with the ‘Ti’ shifted from the centroid of the octahedra formed by ‘O’. This is an example of a Perovskite structure, which have a general formula ABO 3 (other examples are: Sr. Ti. O 3, KTa. O 3, Sr. Sn. O 3, and many more). q In fact Ba. Ti. O 3 [(Ba+2 Ti+4) (O 2)3] can exist in hexagonal, cubic, tetragonal, orthorhombic, and rhombohedral crystal structures. All of these phases exhibit the ferroelectric effect except the cubic phase (with an inversion centre). q Not all Perovskites are ferroelectric, Sr. Ti. O 3 (at RT) with centre of symmetry is cubic (c. P 5, Pm 3 m) and is not a ferroelectric material. In Ba. Ti. O 3 the Ti+4 ion is slightly smaller than the space given by the octahedral position and hence the ion slightly shifts along one of the <001> directions; thus lowering the symmetry of the crystal to tetragonal. This further introduces a permanent dipole to the structure. Note: Sr. Ti. O 3 becomes tetragonal at low T (below 168 C). q Regions within the material where the electric dipoles are parallely oriented (say along [001]) form a ferroelectric domain. In neighbouring domains the dipole may be oriented along one of the other members of the <001> family (e. g. [010]). q Different Perovskites can exhibit a variety of properties like they can be: dielectric (Ca. Ti. O 3), ferroelectric (Ba. Ti. O 3), piezoelectric (Pb(Zr, Ti)O 3), semiconducting ((Ba, La)Ti. O 3), superconducting, etc. (they can even show GMR effect). It is to be noted that some of these compounds have alloying in one of the sublattices and some depend on off-stoichiometry for their properties.

Ba. Ti. O 3 q The structure below 120 is tetragonal (next slide for figures and data) with the Ti+4 ion slightly displaced towards one of the <001> directions.

Ba. Ti. O 3 Ti not at the centre of the cell (slightly displaced up) O Ti Ba Ba. Ti. O 3 Lattice parameter(s) a = 3. 99 Å, c = 4. 033 Å Space Group P 4 mm (99) Strukturbericht notation Pearson symbol Other examples with this structure t. P 5 Wyckoff position Site Symmetry x y z Occ Ba 1 a 4 mm 0 0 0 1 Ti 1 b 4 mm ½ ½ 0. 515 1 O 1 1 b 4 mm ½ ½ 0. 025 1 O 2 2 c 2 mm. 0 ½ 0. 483 1

The displacement of Ti gives Ba. Ti. O 3 a net electric dipole

Sr. Ti. O 3 Ti not at the centre of the cell (unlike in Ba. Ti. O 3) O Ti Sr Sr. Ti. O 3 Lattice parameter(s) a = 3. 90 Å Space Group Pm 3 m (221) Strukturbericht notation Pearson symbol Other examples with this structure c. P 5 Wyckoff position Site Symmetry x y z Occ Ti 1 a m 3 m 0 0 0 1 Sr 1 b m 3 m ½ ½ ½ 1 O 3 d 4/mm. m ½ 0 0 1

Piezoelectricity

Thermal Expansion q When a material is heated it usually expands* (conversely a material will contract on cooling). The strains introduced are stress free strains (i. e. the body will be stress free in the expanded state, in the absence of any external constraints). q Since the stimulus ( T) has no directions involved, the response (thermal strains) must correspond to the symmetry of the crystal. This implies that none of the symmetry elements of a crystal can be destroyed during free thermal expansion. q Thermal expansion (strains) can be related to the temperature change by: 2 nd rank tensor (field) Scalar Thermal expansion coefficient 2 nd rank tensor (material property) Written in full q As strain is a symmetric tensor**, so is the tensor representing the coefficient of thermal expansion. Note that the strain components are scaled-up versions of the coefficients of thermal expansion (with appropriate change in units). * Examples to the contrary exist (in some materials coefficient of thermal expansion may be negative in some temperature regimes). ** In usual materials.

Thermal strains along principal directions § The directions of principal strains will coincide with the principal directions of αij. Along the principal directions the strains are: § This implies that a sphere in the crystal will become an ellipsoid (the strain ellipsoid) on heating/cooling. This is illustrated in the 2 D example below, wherein the new lengths along x 1 & x 2 are: (1+α 1 T) & (1+α 2 T). heat § The coefficient of bulk expansion is: (α 11 + α 22 + α 33) = (α 1 + α 2 + α 3) is an invariant.

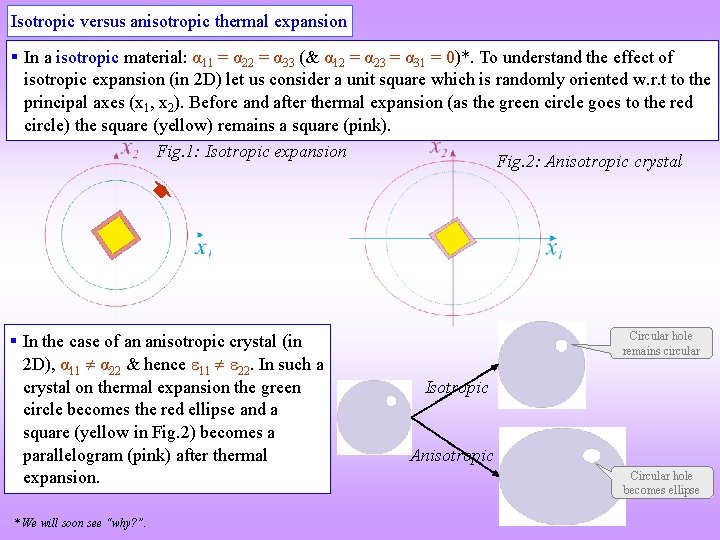
Isotropic versus anisotropic thermal expansion § In a isotropic material: α 11 = α 22 = α 33 (& α 12 = α 23 = α 31 = 0)*. To understand the effect of isotropic expansion (in 2 D) let us consider a unit square which is randomly oriented w. r. t to the principal axes (x 1, x 2). Before and after thermal expansion (as the green circle goes to the red circle) the square (yellow) remains a square (pink). Fig. 1: Isotropic expansion Fig. 2: Anisotropic crystal § In the case of an anisotropic crystal (in 2 D), α 11 α 22 & hence 11 22. In such a crystal on thermal expansion the green circle becomes the red ellipse and a square (yellow in Fig. 2) becomes a parallelogram (pink) after thermal expansion. * We will soon see “why? ”. Circular hole remains circular Isotropic Anisotropic Circular hole becomes ellipse

Symmetry imposed restrictions on the number of independent coefficients We have noted before that axes transformations can be carried out by: Let us consider a cubic crystal with (4/m 3 2/m) symmetry (highest available for cubic crystals) 4 -fold along Z 3 Like in tetragonal crystals By Neumann’s principle: § If a crystal had only a 4 -fold axis then, two independent coefficients would survive: α 11 & α 33. This implies that all tetragonal crystals have only two independent coefficients (out of a possible 6). § It is to be noted that though we are deriving the effect of symmetry on thermal expansion coefficients, it is applicable to all 2 nd order tensor properties (as there is nothing specific to thermal expansion coefficient in the matrix operations).

Now we apply the other symmetry operation m Z 3 (after the 4 -fold operation) m Z 3 We got no reduction in the number of coefficients based on the mirror plane. Now we try the 3 -fold along [111]. 3 -fold || [111] Which is present in all cubic crystals By Neumann’s principle: § This implies that for (4/m 3 2/m) crystals there is only one independent coefficient. § We could have change the order of the operations (i. e. we could have operated the 3 -fold first) and this should not make any difference. Also, we could have operated the 3 instead of the 3 -fold (as this is available for the (4/m 3 2/m) crystals.

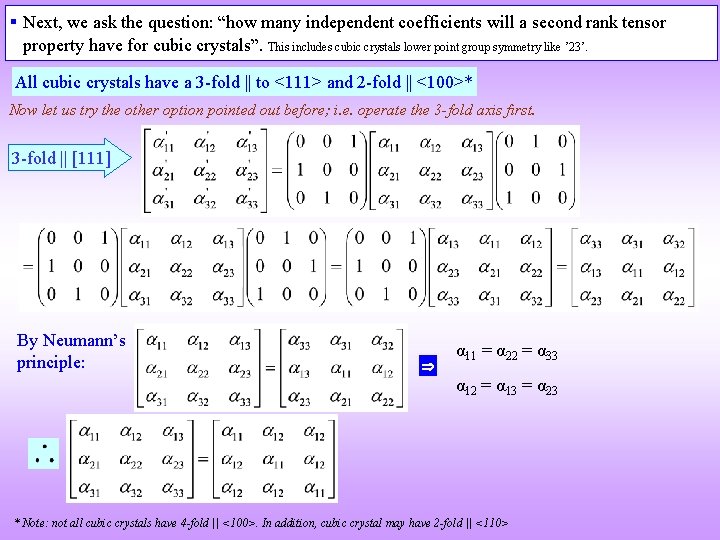
§ Next, we ask the question: “how many independent coefficients will a second rank tensor property have for cubic crystals”. This includes cubic crystals lower point group symmetry like ’ 23’. All cubic crystals have a 3 -fold || to <111> and 2 -fold || <100>* Now let us try the other option pointed out before; i. e. operate the 3 -fold axis first. 3 -fold || [111] By Neumann’s principle: α 11 = α 22 = α 33 α 12 = α 13 = α 23 * Note: not all cubic crystals have 4 -fold || <100>. In addition, cubic crystal may have 2 -fold || <110>

Next we operate the 2 -fold || [001] By Neumann’s principle: α 12 = 0 All cubic crystals are isotropic with respect to second rank tensor properties (require only one independent constant).

Centrosymmetry in 2 nd rank tensor properties q Let us consider a vector stimulus qj connected to a vector response pi via a tensor property Tij. Let us reverse the direction of the stimulus, this will reverse the direction of the response without affecting Tij. q This implies that all second rank tensor properties are centrosymmetrical. Reversing stimulus

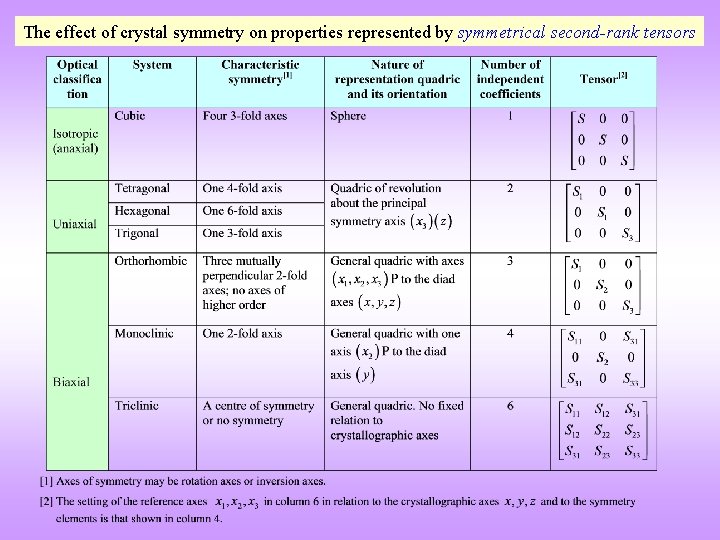
The effect of crystal symmetry on properties represented by symmetrical second-rank tensors

4 th Order Tensor Properties (mechanics) q The stresses are related to strains by Hooke’s law via the 4 th order tensor properties: Stiffness (Eijkl) and Compliance (Sijkl). Note: Usually ‘C’ is the symbol for stiffness and the symbol for compliance is not ‘C’ and confusing with ‘Stiffness’! q Being 4 th order tensors there are 3× 3× 3× 3 (= 81) components (in 3 D). Not all these components are independent. The number of independent components reduces 81 to 36 given that stress and strain are symmetric tensors. For diagonal terms: is a symmetric tensor: q S 1112 & S 1121 always occur together and cannot be experimentally separated and keeping this in view S 1112 is assumed to be equal to S 1121. For off-diagonal terms: As 12 = 21 As ‘ij’ & ‘kl’ refer to strain & stress tensors which have 6 independent components (3 D) 9× 9 If all components are independent Thus not all components are independent 6× 6

The single index notation for stress & strain Voigt’s notation q Sometimes the indices are condensed (from 2 to 1) according to the notation as below. The two index notation is the matrix notation and has to be converted back to tensor notation so that transformations can be carried out (as usual for tensors). Only one symmetric half of the matrix is written Tensor Matrix This will lead to condensed notation version of the stress-strain relation (matrix form) E. g. Tensor Matrix

q Further reduction in the number of independent moduli is possible using the concept of strain energy of a hyper-elastic material. If ‘W’ is the strain energy per unit volume: q Let us consider the specific case where the only stress applied is 11 (= 1 in condensed index notation) and the body is in plane strain condition (i. e. 13, 23 & 33 are zero). The strain energy is given by (Taylor series expansion for small strain in a hyperelastic material): Zero if no residual strain Zero if no residual stress Ignoring higher order terms and observing that the quantity in blue font is Eijkl Noting that the order of differentiation does not matter Eijkl is a symmetric tensor

Effect of symmetry elements on Eijkl q We have noted that even for crystals without any symmetry, only 21 of the 81 possible elastic constants are independent. For crystals with symmetry this number is further reduced. Let us consider a tetragonal crystal with 4 symmetry. q The 4 -fold will take: (a) (b), (b) ( a), (c). Matrix of surviving coefficients is shaded blue only 7 independent terms survive: E 1111, E 3333, E 1122, E 1133, E 1313, E 1212, E 1112. 1131=1113=2223=2232= 1113 all these coefficients are zero 2213=1123=1132=2231=2213 all these coefficients are zero 3331=3332=3323= 3313= 3331 all these coefficients are zero 2312=3221=1321=3112= 3221 all these coefficients are zero 3312= 3321= 3312 all these coefficients are zero 2331= 1332= 3213= 2331 all these coefficients are zero

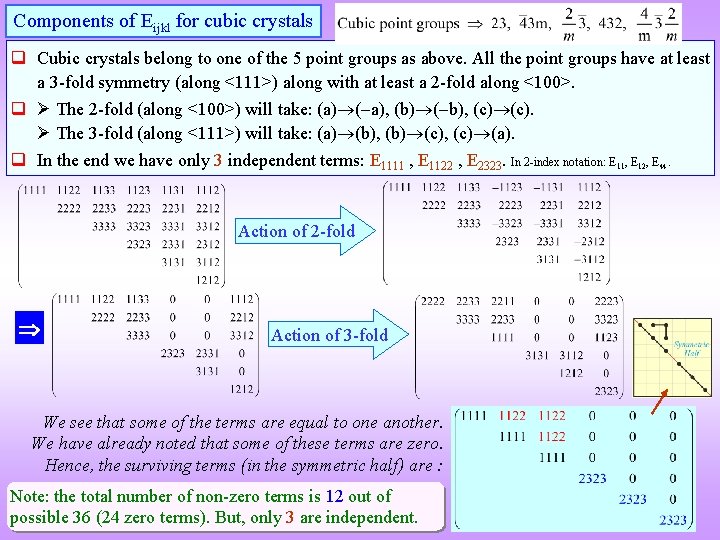
Components of Eijkl for cubic crystals q Cubic crystals belong to one of the 5 point groups as above. All the point groups have at least a 3 -fold symmetry (along <111>) along with at least a 2 -fold along <100>. q The 2 -fold (along <100>) will take: (a) ( a), (b) ( b), (c). The 3 -fold (along <111>) will take: (a) (b), (b) (c), (c) (a). q In the end we have only 3 independent terms: E 1111 , E 1122 , E 2323. In 2 -index notation: E 11, E 12, E 44. Action of 2 -fold Action of 3 -fold We see that some of the terms are equal to one another. We have already noted that some of these terms are zero. Hence, the surviving terms (in the symmetric half) are : Note: the total number of non-zero terms is 12 out of possible 36 (24 zero terms). But, only 3 are independent.

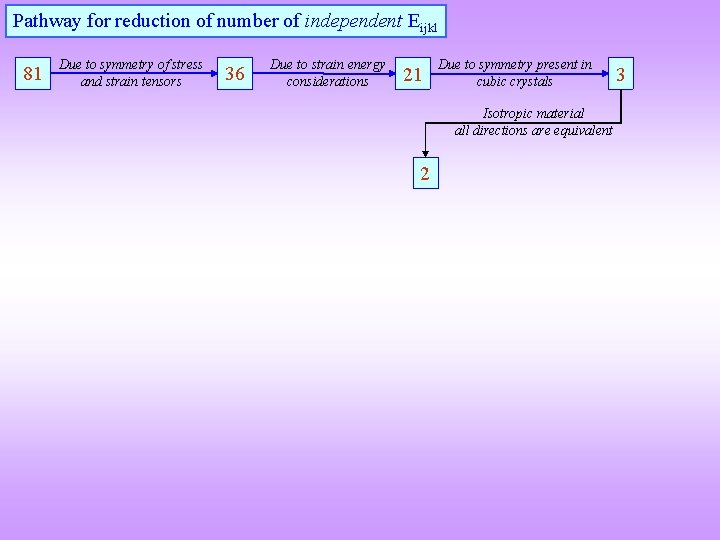
Pathway for reduction of number of independent Eijkl 81 Due to symmetry of stress and strain tensors 36 Due to strain energy considerations 21 Due to symmetry present in cubic crystals Isotropic material all directions are equivalent 2 3

Curie* Principle Click here for introduction to Curie groups q When certain stimuli lead to certain responses, the symmetry elements of the stimuli should be seen in the response. Alternate statement: “the symmetries of the causes are to be found in the effects”. q A crystal subjected to certain stimulus will display only those symmetry elements, which are common to the crystal without the stimulus and the stimulus without the crystal. q In terms of groups this can be written as: q The symmetry of the crystal in the presence of the stimulus is the intersection group of the symmetry of the crystal (in the absence of the stimulus) with the symmetry of the stimulus (in the absence of the crystal). q R, G, S are point groups (and not space groups). § Let us consider a cubic crystal with 4/m 3 2/m symmetry, which is loaded along [111] direction. The symmetry of the stimulus is m (‘conical’ symmetry). The symmetry of the strained crystal is 3 m (the common symmetry to both the crystal and the stimulus). * Pierre Curie, 1894.

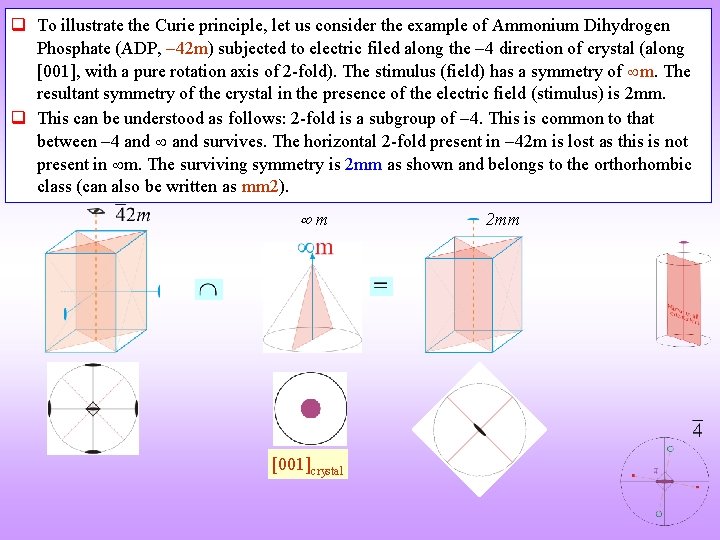
q To illustrate the Curie principle, let us consider the example of Ammonium Dihydrogen Phosphate (ADP, 42 m) subjected to electric filed along the 4 direction of crystal (along [001], with a pure rotation axis of 2 -fold). The stimulus (field) has a symmetry of m. The resultant symmetry of the crystal in the presence of the electric field (stimulus) is 2 mm. q This can be understood as follows: 2 -fold is a subgroup of 4. This is common to that between 4 and survives. The horizontal 2 -fold present in 42 m is lost as this is not present in m. The surviving symmetry is 2 mm as shown and belongs to the orthorhombic class (can also be written as mm 2). m [001]crystal 2 mm

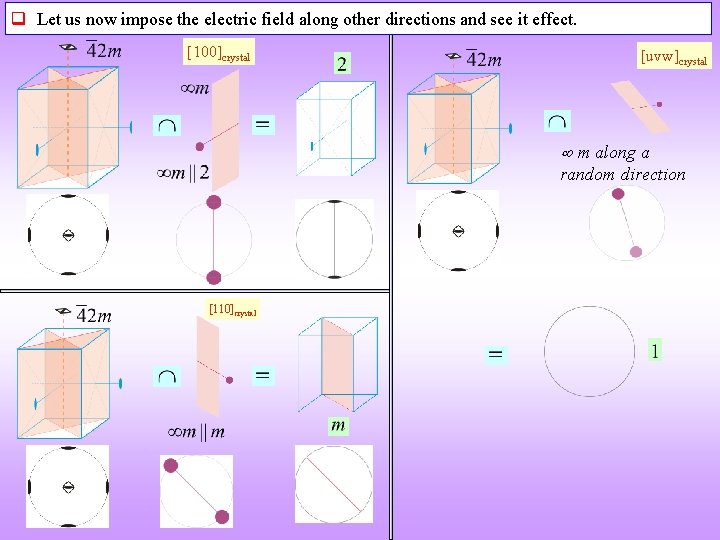
q Let us now impose the electric field along other directions and see it effect. [100]crystal [uvw]crystal m along a random direction [110]crystal

Taking partial derivatives (1 st wrt to 22 then wrt 11) 1 Now reversing the order of the partial derivatives (1 st wrt to 11 then wrt 22 ) 2 Since the order of differentiation should not matter as far as the energy density (W) is concerned, (1) = (2). This implies E 1122 = E 2211.

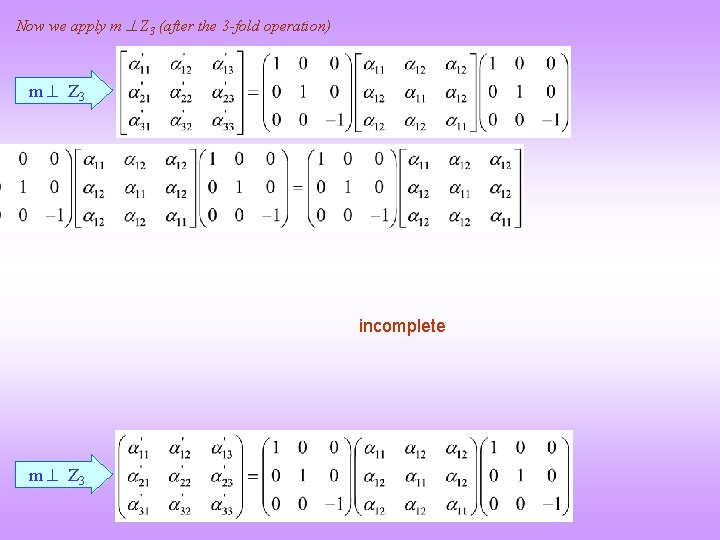
Now we apply m Z 3 (after the 3 -fold operation) m Z 3 incomplete m Z 3

End

In ppt Get cif file