Sugrkvets raycasting raytracing SzirmayKalos Lszl Kpszintzis pixel Loklis

Sugárkövetés: ray-casting, ray-tracing Szirmay-Kalos László

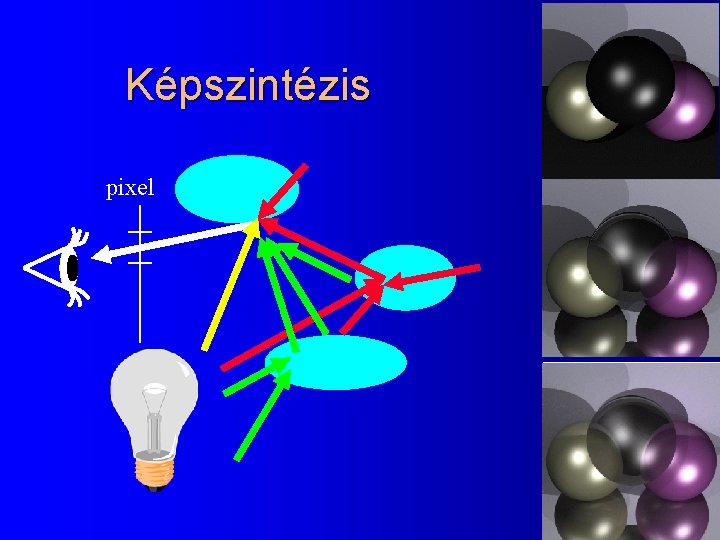
Képszintézis pixel

Lokális illuminációs módszer L(x, )=Le(x, )+ L(h(x, - ), ) fr ( ’, x, ) cos ’d ’ l A jobb oldali radiancia: – fényforrások emissziója l Fényforrások fényének egyszeri visszaverődését számítjuk L (x, )=Le(x, )+ Llightsource fr ( ’, x, ) cos ’d ’ Le(y, ’)

Absztrakt fényforrás modellek: az integrálást megspórolják l l l Ambiens fényforrás: La constant – ambiens visszaverődési modell: Lref = La ka – konstans égbolt fény modell: Lref = La a(x, view dir) Irány fényforrások: egyetlen irányba sugároz, a fénysugarak párhuzamosak, az intenzitás független a pozíciótól Pozicionális fényforrás: egyetlen pontból sugároz, az intenzitás a távolság négyzetével csökken d irány pozicionális

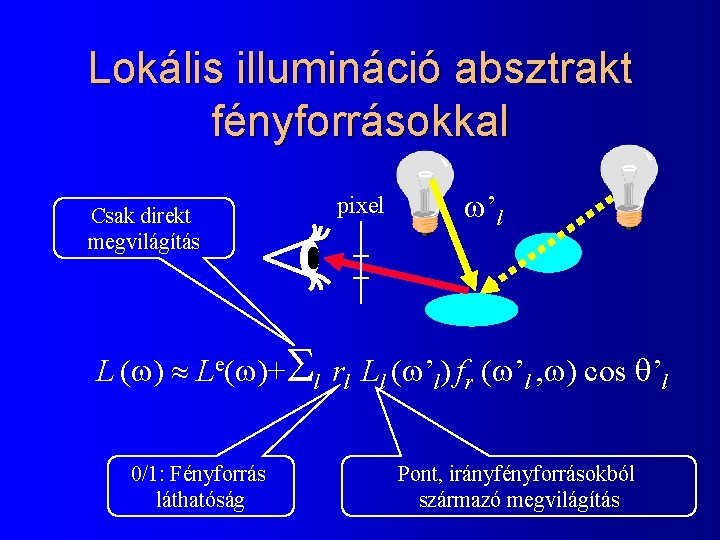
Lokális illumináció absztrakt fényforrásokkal Csak direkt megvilágítás pixel ’l L ( ) Le( )+Sl rl Ll ( ’l) fr ( ’l , ) cos ’l 0/1: Fényforrás láthatóság Pont, irányfényforrásokból származó megvilágítás

Ambiens tag Lokális illumináció + ambiens tag L ( ) Le( )+Sl rl Ll ( ’l) fr ( ’l , ) cos ’l + ka La

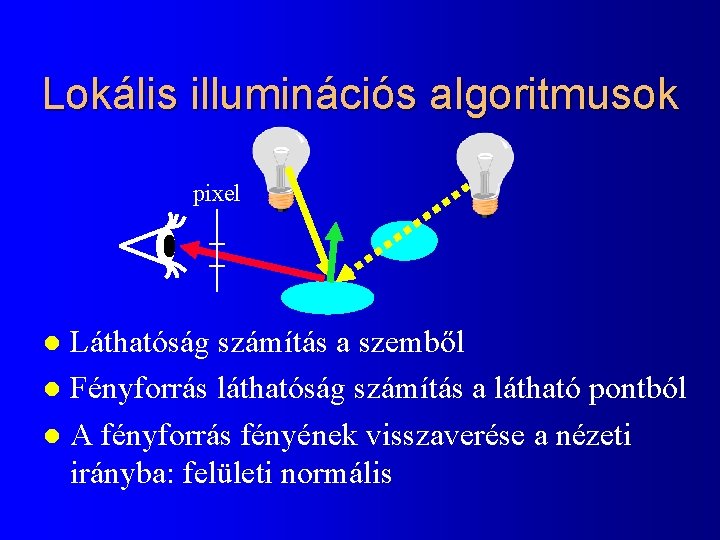
Lokális illuminációs algoritmusok pixel Láthatóság számítás a szemből l Fényforrás láthatóság számítás a látható pontból l A fényforrás fényének visszaverése a nézeti irányba: felületi normális l

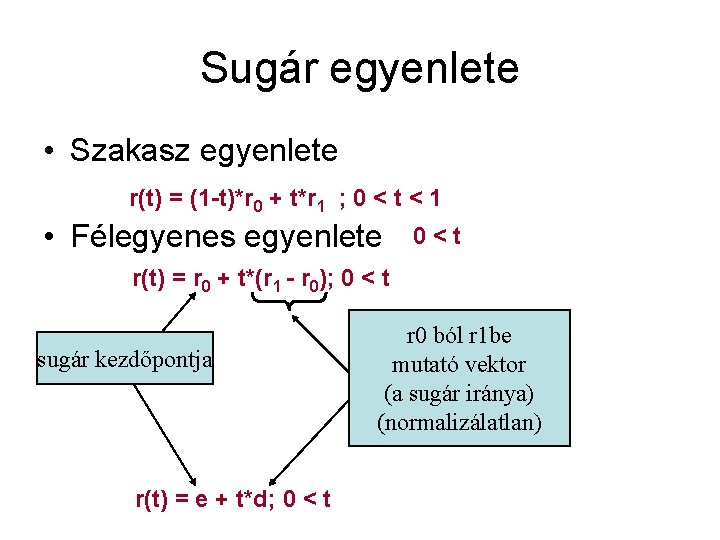
Sugár egyenlete • Szakasz egyenlete r(t) = (1 -t)*r 0 + t*r 1 ; 0 < t < 1 • Félegyenes egyenlete 0<t r(t) = r 0 + t*(r 1 - r 0); 0 < t sugár kezdőpontja r(t) = e + t*d; 0 < t r 0 ból r 1 be mutató vektor (a sugár iránya) (normalizálatlan)

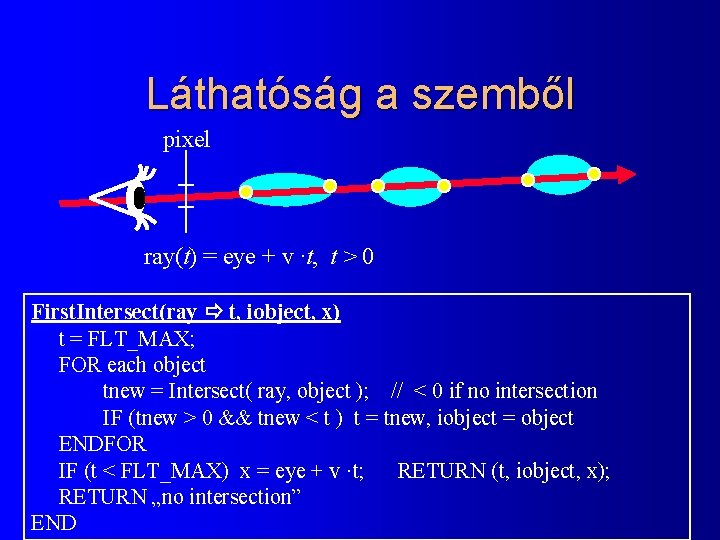
Láthatóság a szemből pixel ray(t) = eye + v ·t, t > 0 First. Intersect(ray t, iobject, x) t = FLT_MAX; FOR each object tnew = Intersect( ray, object ); // < 0 if no intersection IF (tnew > 0 && tnew < t ) t = tnew, iobject = object ENDFOR IF (t < FLT_MAX) x = eye + v ·t; RETURN (t, iobject, x); RETURN „no intersection” END

Metszéspont számítás gömbbel |r - center |2 = R 2 r R center Nincs gyök 1 gyök 2 gyök |ray(t) - center |2 = R 2 (v ·v) t 2 + 2 ((eye-center) ·v) t +((eye-center) ·(eye-center))- R 2 = 0 Wanted: minimum pozitív megoldás Felületi normális: (ray(t) - center)/R

Kvadratikus felületek x Kvadratikus felület: [x, y, z, 1] A y = 0 z 1 Ellipszoid 2 2 z 2 x y + + -1=0 a 2 b 2 c 2 Végtelen kúp x 2 y 2 2 2 + - z =0 2 a b Másodfokú egyenlet Végtelen henger x 2 y 2 + 2 - 1 =0 2 a b

Példa: sugár metszéspontja kvadratikus felülettel • Felület egyenlete legyen 3 x 2 + 2 xy + z 2 + 2 z - 7 = 0 • Ugyanez mátrixformában xyz 1 3 0 0 0 2 0 0 0 0 1 2 0 -7 x y z 1 =0

Sugár egyenlete • A sugár kezdőpontja legyen E = [0 1 0] és az iránya D = [1 1 0] x(t) = ex + dxt = 0 + 1 t = t y(t) = ey + dyt = 1 + 1 t = 1 + t z(t) = ez + dzt = 0 + 0 t = 0 • Írjuk vissza ebbe: másodfokú egyenlet (-b √(b 2 -4 ac))/2 a 3 x 2 + 2 xy + z 2 + 2 z - 7 = 0 3*t*t + 2*t*(1+t) + 0*0 + 2*0 - 7 = 0 3 t 2 + 2 t -7 = 0 ebből a legkisebb 5 t 2 + 2 t - 7 = 0 pozitív t=1 t = [-2 √(2*2 - 4*5*(-7))] /(2*5) = [-2 √ 144]/10 = [-2 12]/10; t 1= -1. 4, t 2 = 1

Metszéspont • Sugár egyenletébe t=1 x(t) = ex + dxt = 0 + 1 t = 1 y(t) = ey + dyt = 1 + 1 t = 1 + t = 2 z(t) = ez + dzt = 0 + 0 t = 0 • A metszéspont [1 2 0]ban van

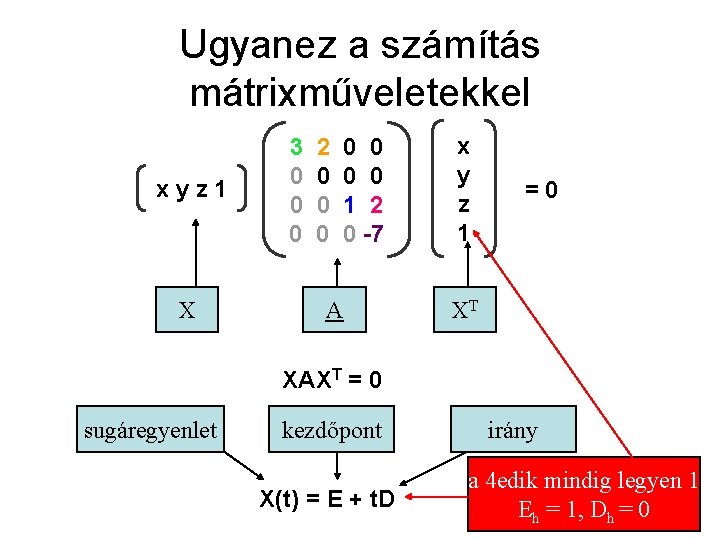
Ugyanez a számítás mátrixműveletekkel xyz 1 X 3 0 0 0 2 0 0 0 0 1 2 0 -7 A x y z 1 =0 XT XAXT = 0 sugáregyenlet kezdőpont X(t) = E + t. D irány a 4 edik mindig legyen 1 Eh = 1, Dh = 0

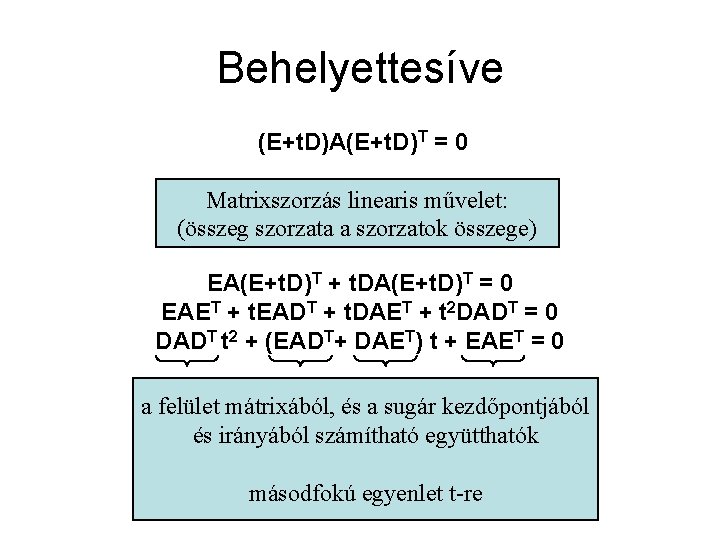
Behelyettesíve (E+t. D)A(E+t. D)T = 0 Matrixszorzás linearis művelet: (összeg szorzata a szorzatok összege) EA(E+t. D)T + t. DA(E+t. D)T = 0 EAET + t. EADT + t. DAET + t 2 DADT = 0 DADT t 2 + (EADT+ DAET) t + EAET = 0 a felület mátrixából, és a sugár kezdőpontjából és irányából számítható együtthatók másodfokú egyenlet t-re

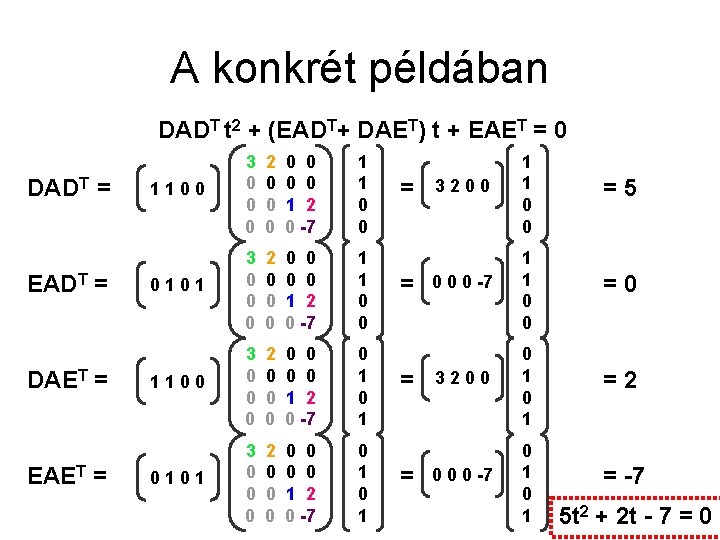
A konkrét példában DADT t 2 + (EADT+ DAET) t + EAET = 0 DADT = EADT = DAET = EAET = 1100 3 0 0 0 2 0 0 0 0 1 2 0 -7 1 1 0 0 0101 3 0 0 0 2 0 0 0 0 1 2 0 -7 1 1 0 0 1100 3 0 0 0 2 0 0 0 0 1 2 0 -7 0 1 0101 3 0 0 0 2 0 0 0 0 1 2 0 -7 0 1 = = 3200 1 1 0 0 =5 0 0 0 -7 1 1 0 0 =0 3200 0 1 =2 0 0 0 -7 0 1 = -7 5 t 2 + 2 t - 7 = 0

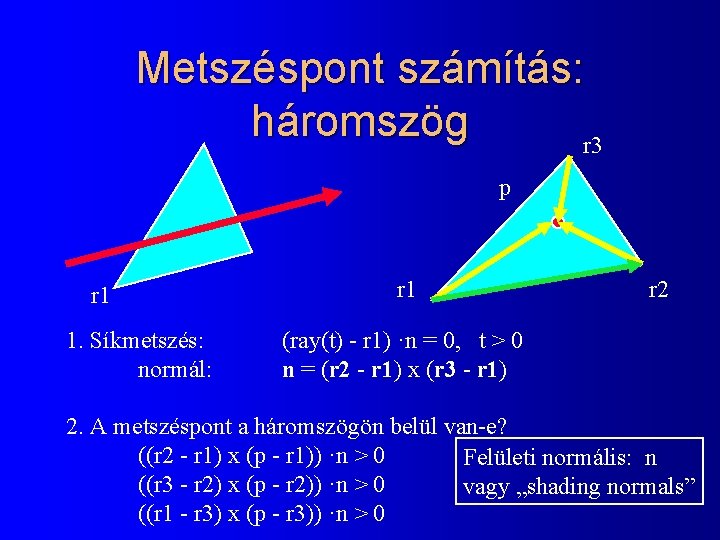
Metszéspont számítás: háromszög r 3 p r 1 1. Síkmetszés: normál: r 1 r 2 (ray(t) - r 1) ·n = 0, t > 0 n = (r 2 - r 1) x (r 3 - r 1) 2. A metszéspont a háromszögön belül van-e? ((r 2 - r 1) x (p - r 1)) ·n > 0 Felületi normális: n ((r 3 - r 2) x (p - r 2)) ·n > 0 vagy „shading normals” ((r 1 - r 3) x (p - r 3)) ·n > 0

Példa: hsz-sugár metszéspont • Sugár kezdőpont [0 2 0], irány [0 0 1] • Háromszög csúcsai: – [0 3 2], [1 1 1], [-1 2 1] • Hsz síkjának egyenlete – normál n = ([1 1 1] - [0 3 2])×([-1 2 1] - [0 3 2]) = [1 -2 -1]×[-1 -1 -1] = [1 2 -3] – síkegyenet Ax + By + Cz + D = 0 x + 2 y - 3 z + D = 0 – egyik csúcsot [1 1 1] beírva kapjuk Dt 1 + 2 - 3 + D = 0; x + 2 y - 3 z = 0

Sík-sugár metszéspont • Sík • Sugár x + 2 y - 3 z = 0 x = 0 + 0 t = 0 y = 2 + 0 t = 2 z = 0 + 1 t = t • Sugár beírva a síkba 0 + 2 - 3 t = 0 t = 2/3 • Metszéspont (t vissza a sugáregyenletbe) [0 2 2/3]

[0 2 2/3] [0 3 2], [1 1 1], [-1 2 1] Benne van-e a hszben ((r 2 - r 1) x (p - r 1)) ·n > 0 ((r 3 - r 2) x (p - r 2)) ·n > 0 ((r 1 - r 3) x (p - r 3)) ·n > 0 [1 -2 -1]×[-1 1 -1/3] = [5/3 4/3 -1]·[1 2 -3] = 5/3 + 8/3 + 3 > 0 stb… ha mind igaz, a pont bent van a hszben ha nem, a sugár nem metszi a hszt

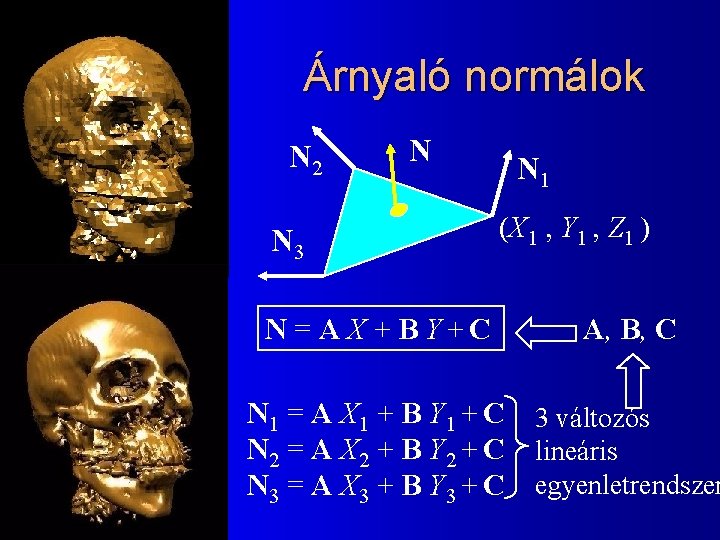
Árnyaló normálok N 2 N N 3 N 1 (X 1 , Y 1 , Z 1 ) N = A X + B Y+C A, B, C N 1 = A X 1 + B Y 1 + C N 2 = A X 2 + B Y 2 + C N 3 = A X 3 + B Y 3 + C 3 változós lineáris egyenletrendszer

Parametrikus felületek r(u, v), u, v in [0, 1] ray(t) = eye + v ·t, t > 0 r(u, v) = ray(t) Egyenlet megoldás: u, v, t Teszt: 0< u, v < 1, t>0 r(0, 0) r(0, 0. 5) r(0. 5, 0) r(1, 0) r(0, 1) r(0. 5, 0. 5) r(1, 1) Rekurzív tesszelláció

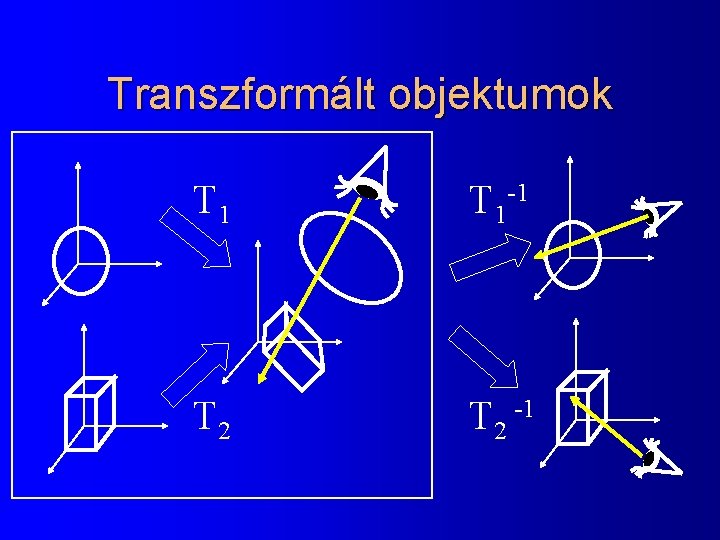
Transzformált objektumok T 1 -1 T 2 -1

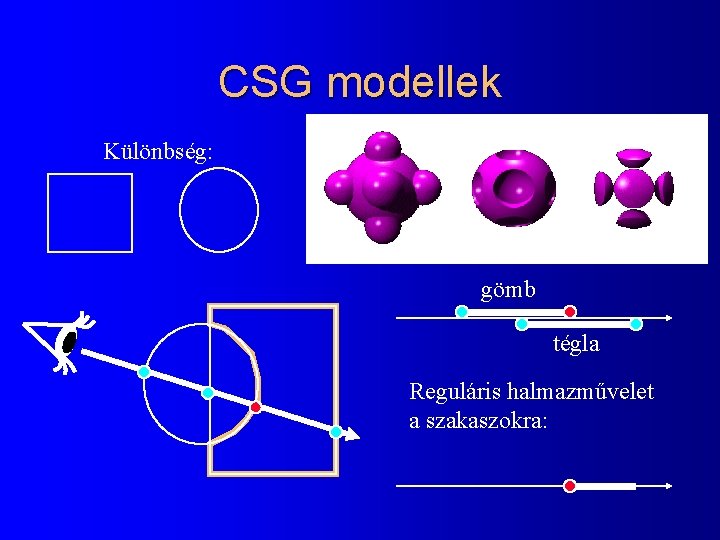
CSG modellek Különbség: gömb tégla Reguláris halmazművelet a szakaszokra:

Ray-casting képek Lokális illumináció valós idő Lokális illumináció + árnyékok 0. 1 sec … 1 sec

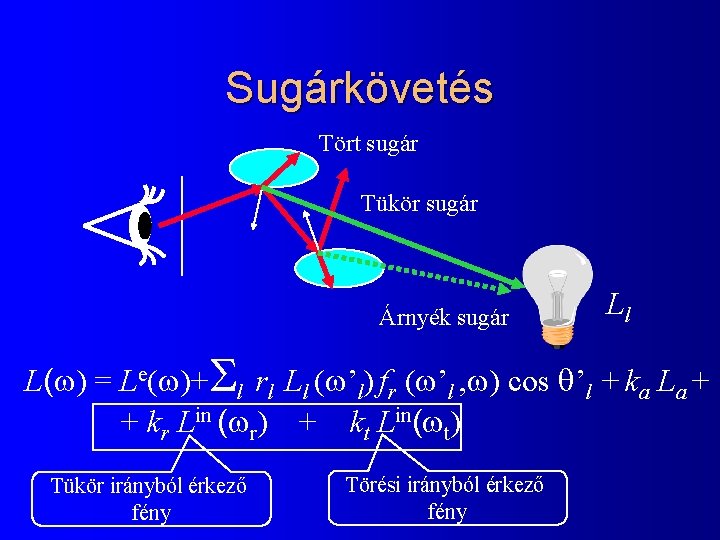
Sugárkövetés Tört sugár Tükör sugár Árnyék sugár Ll L( ) = Le( )+Sl rl Ll ( ’l) fr ( ’l , ) cos ’l + ka La + + kr Lin ( r) + kt Lin( t) Tükör irányból érkező fény Törési irányból érkező fény

Sugárkövetés lépései l A szembe a pixel irányából érkező sugársűrűség – Adott irányba látható felületi pont és normálvektor – A felületi pontból látható fényforrások – A felületi pontban a tükör és törési irány – A tükör irányból érkező sugársűrűség – A törési irányból érkező sugársűrűség Rekurzió – Az árnyalási egyenlet kiértékelése

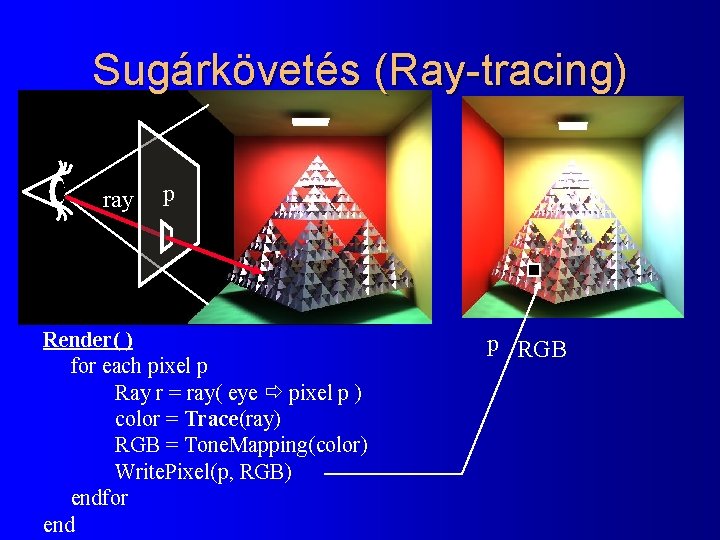
Sugárkövetés (Ray-tracing) ray p Render( ) for each pixel p Ray r = ray( eye pixel p ) color = Trace(ray) RGB = Tone. Mapping(color) Write. Pixel(p, RGB) endfor end p RGB

Sugárkövetés: Trace függvény Color Trace( ray ) ray IF (First. Intersect(ray object, x)>0 ) RETURN La ENDIF color = Le (x, -ray. dir) color += Direct Lightsource(x, -ray. dir) IF ( kr > 0 ) THEN Reflect. Dir( ray, reflected ray) color += kr · Trace( reflected ray ) ENDIF IF ( kt > 0 && Refract. Dir( ray, refracted ray ) ) color += kt · Trace( refracted ray ) ENDIF RETURN color x

Sugárkövetés: Trace függvény Color Trace( ray, d) IF d > dmax THEN RETURN La IF (First. Intersect(ray object, x) > 0) RETURN La ENDIF color = Le (x, -ray. dir) color += Direct Lightsource(x, -ray. dir) IF ( kr > 0 ) THEN Reflect. Dir( ray, reflected ray) color += kr · Trace( reflected ray, d+1 ) ENDIF IF ( kt > 0 && Refract. Dir( ray, refracted ray ) ) color += kt · Trace( refracted ray, d+1 ) ENDIF RETURN color ray x

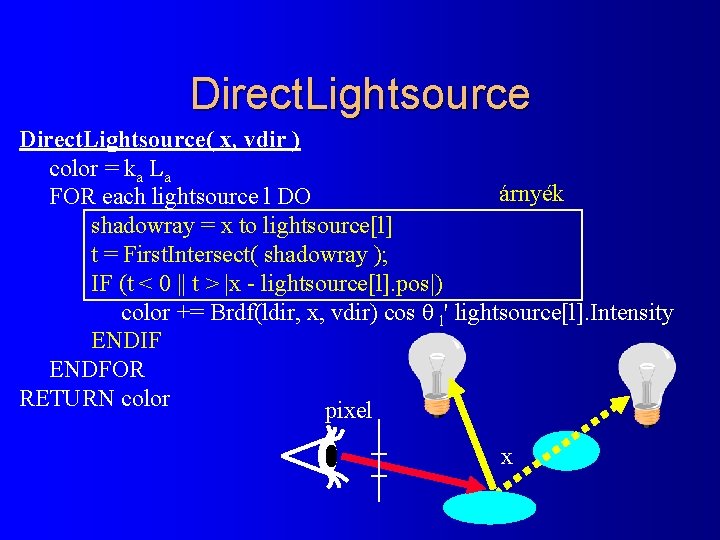
Direct. Lightsource( x, vdir ) color = ka La árnyék FOR each lightsource l DO shadowray = x to lightsource[l] t = First. Intersect( shadowray ); IF (t < 0 || t > |x - lightsource[l]. pos|) color += Brdf(ldir, x, vdir) cos l' lightsource[l]. Intensity ENDIF ENDFOR RETURN color pixel x

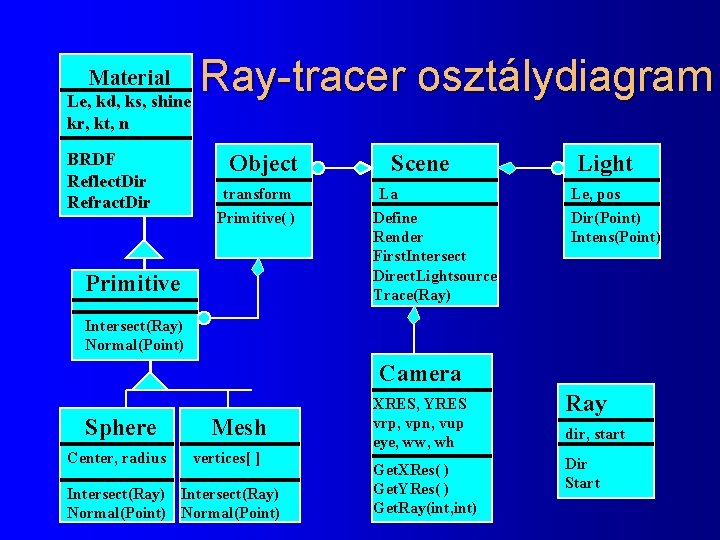
Ray-tracer osztálydiagram Le, kd, ks, shine Material kr, kt, n BRDF Reflect. Dir Refract. Dir Object transform Primitive( ) Primitive Scene La Define Render First. Intersect Direct. Lightsource Trace(Ray) Light Le, pos Dir(Point) Intens(Point) Intersect(Ray) Normal(Point) Camera Sphere Center, radius Mesh vertices[ ] Intersect(Ray) Normal(Point) XRES, YRES vrp, vpn, vup eye, ww, wh Ray Get. XRes( ) Get. YRes( ) Get. Ray(int, int) Dir Start dir, start

Sugárkövetés: eredmény Számítási idő Pixelszám x Objektumszám x (Fényforrás szám+1)

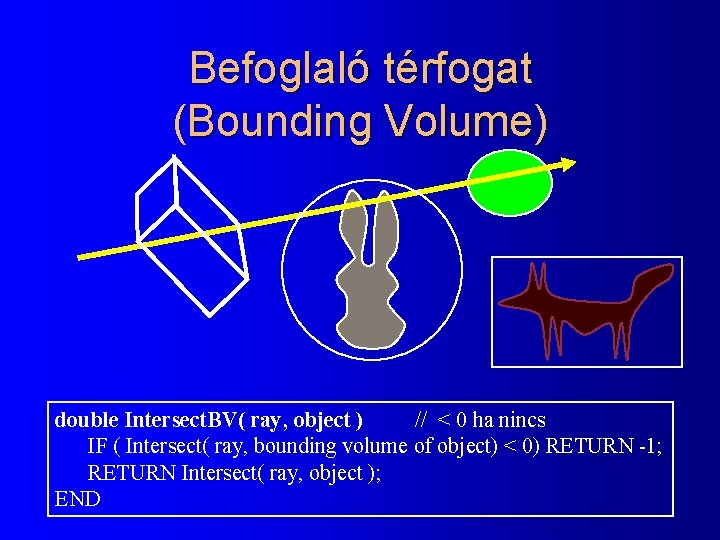
Befoglaló térfogat (Bounding Volume) double Intersect. BV( ray, object ) // < 0 ha nincs IF ( Intersect( ray, bounding volume of object) < 0) RETURN -1; RETURN Intersect( ray, object ); END

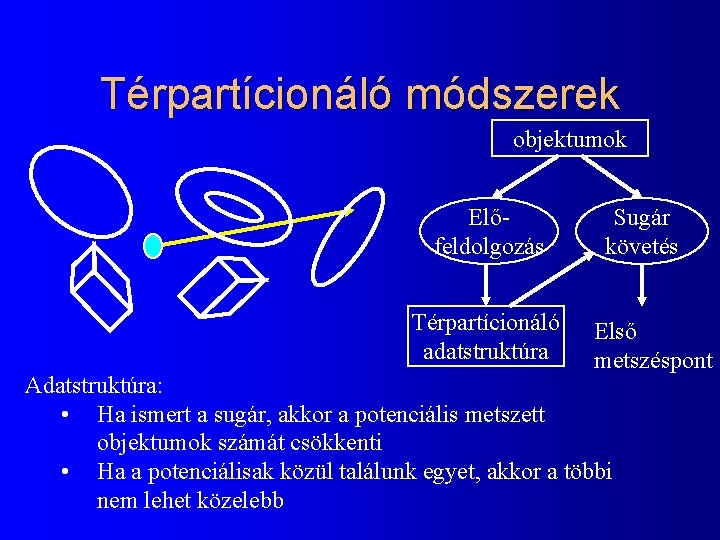
Térpartícionáló módszerek objektumok Előfeldolgozás Térpartícionáló adatstruktúra Sugár követés Első metszéspont Adatstruktúra: • Ha ismert a sugár, akkor a potenciális metszett objektumok számát csökkenti • Ha a potenciálisak közül találunk egyet, akkor a többi nem lehet közelebb

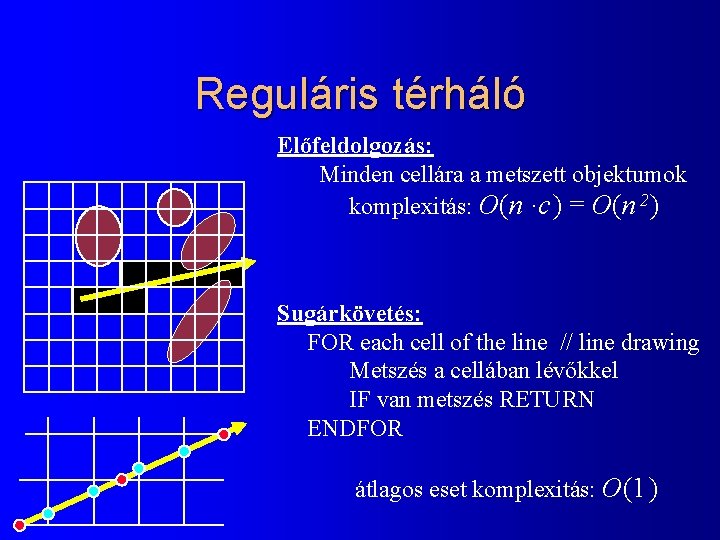
Reguláris térháló Előfeldolgozás: Minden cellára a metszett objektumok komplexitás: O(n ·c ) = O(n 2) Sugárkövetés: FOR each cell of the line // line drawing Metszés a cellában lévőkkel IF van metszés RETURN ENDFOR átlagos eset komplexitás: O(1 )

Cellák bejárására algoritmus Nyilvántartjuk, mely t sugárparaméternél lépjük át a következő x, y, z irányú cellahatároló síkot, (Cx, Cy, Cz) a cellaméret – kezdetben Ix = Ex / Cx változás ebben a cellában vagyunk Tx = (Ix+1)Cx/Dx ennél a t értéknél lépünk Ix += 1 Tx += Cx/Dx Tx, Ty, Tz; kiválasztjuk a legkisebbet frissítjük I-t és T-t

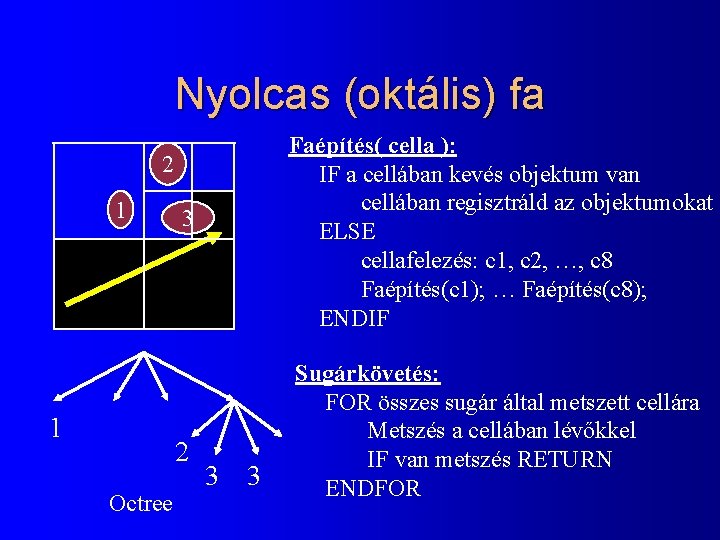
Nyolcas (oktális) fa Faépítés( cella ): IF a cellában kevés objektum van cellában regisztráld az objektumokat ELSE cellafelezés: c 1, c 2, …, c 8 Faépítés(c 1); … Faépítés(c 8); ENDIF 2 1 1 3 2 Octree 3 3 Sugárkövetés: FOR összes sugár által metszett cellára Metszés a cellában lévőkkel IF van metszés RETURN ENDFOR

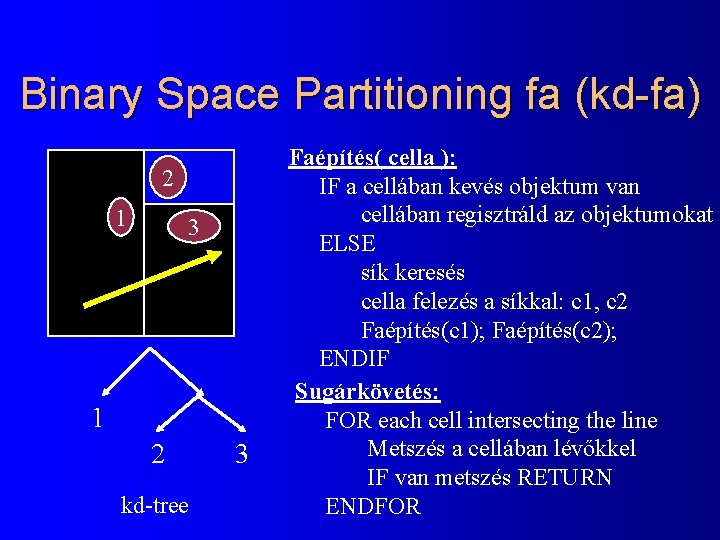
Binary Space Partitioning fa (kd-fa) 2 1 3 1 2 kd-tree 3 Faépítés( cella ): IF a cellában kevés objektum van cellában regisztráld az objektumokat ELSE sík keresés cella felezés a síkkal: c 1, c 2 Faépítés(c 1); Faépítés(c 2); ENDIF Sugárkövetés: FOR each cell intersecting the line Metszés a cellában lévőkkel IF van metszés RETURN ENDFOR