Stats 2022 n NonParametric Approaches to Data Chp

Stats 2022 n Non-Parametric Approaches to Data Chp 15. 5 & Appendix E

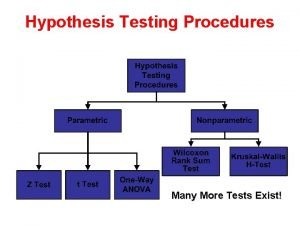
Outline Chp 15. 5 Spearman Correlation Example alternative to Pearson correlation Appendix E Mann - Whitney U-Test Example Wilcoxon signed-rank test Example Kruskal – Wallace Test Friedman Test independent measures t test repeated-measures t test independent measures ANOVA) (repeated measures ANOVA)

A note on ordinal scales • An ordinal scale : Example – Grades

A note on ordinal scales Ordinal scales allow ranking Example – Grades

Why use ordinal scales? • Some data is easier collected as ordinal – –

The case for ranking data 1. Ordinal data needs to be ranked before it can be tested (via non-parametric tests) 2. Transforming data through ranking can be a useful tool

The case for ranking data Ranking data (rank transform) can be a useful tool – If assumptions of a test are not (or cannot be) met… – Common if data has: • Non linear relationship … • Unequal variance… • High variance … – Data sometimes requires rank transformation for analysis

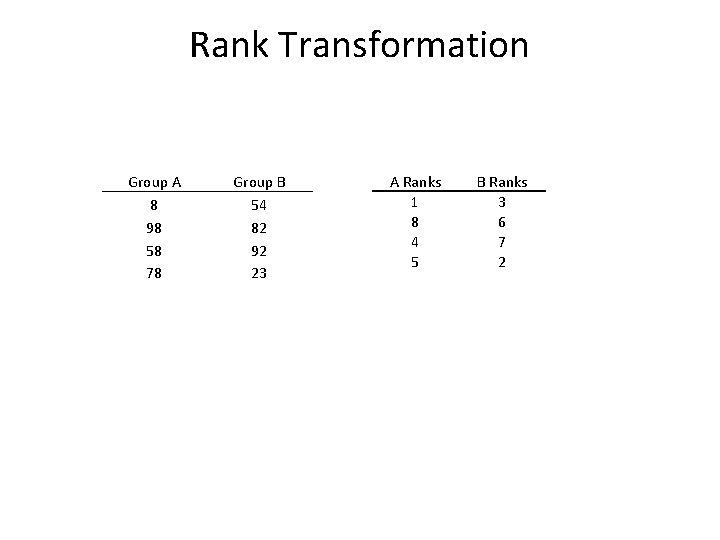
Rank Transformation Group A 8 98 58 78 Group B 54 82 92 23 A Ranks 1 8 4 5 B Ranks 3 6 7 2

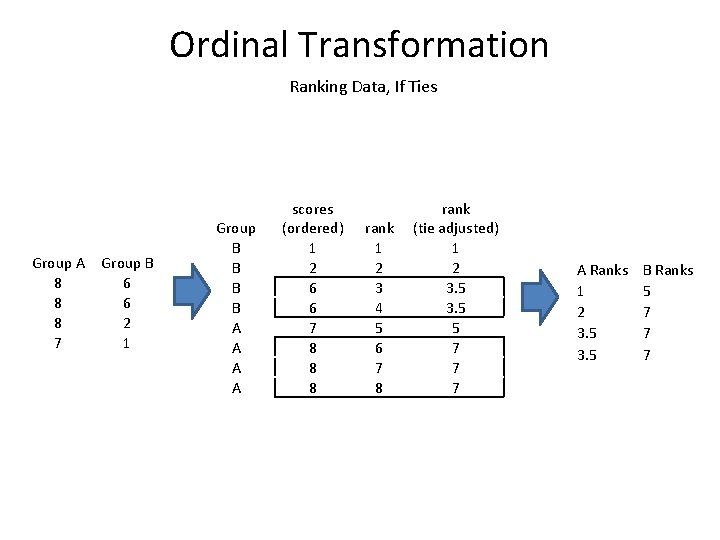
Rank Transformation What if ties? . . Group A 8 8 8 7 Group B 6 6 2 1

Ordinal Transformation Ranking Data, If Ties Group A Group B 8 6 8 2 7 1 Group B B A A scores (ordered) 1 2 6 6 7 8 8 8 rank 1 2 3 4 5 6 7 8 rank (tie adjusted) 1 2 3. 5 5 7 7 7 A Ranks 1 2 3. 5 B Ranks 5 7 7 7

Chp 15. 5 Spearman Correlation

Spearman Correlation Only requirement – ability to rank order data • Data already ranked • Rank transformed data Rank transform useful if relationship non-linear…

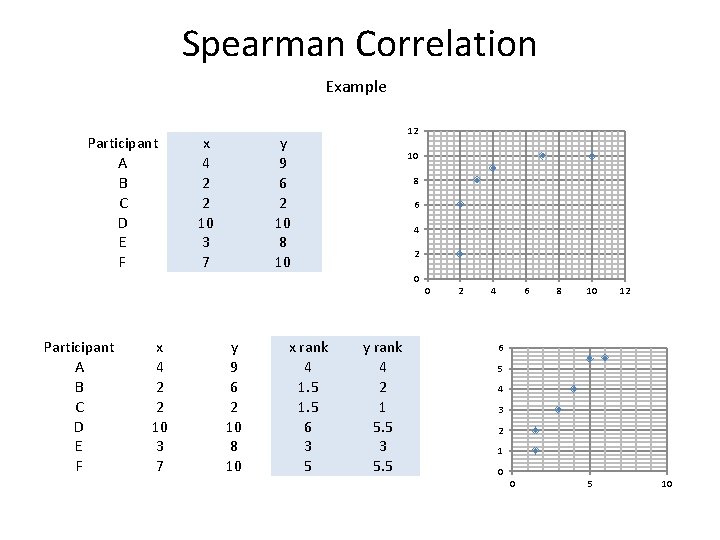
Spearman Correlation Example Participant A B C D E F x 4 2 2 10 3 7 12 y 9 6 2 10 8 10 10 8 6 4 2 0 0 Participant A B C D E F x 4 2 2 10 3 7 y 9 6 2 10 8 10 x rank 4 1. 5 6 3 5 y rank 4 2 1 5. 5 3 5. 5 2 4 6 8 10 12 6 5 4 3 2 1 0 0 5 10

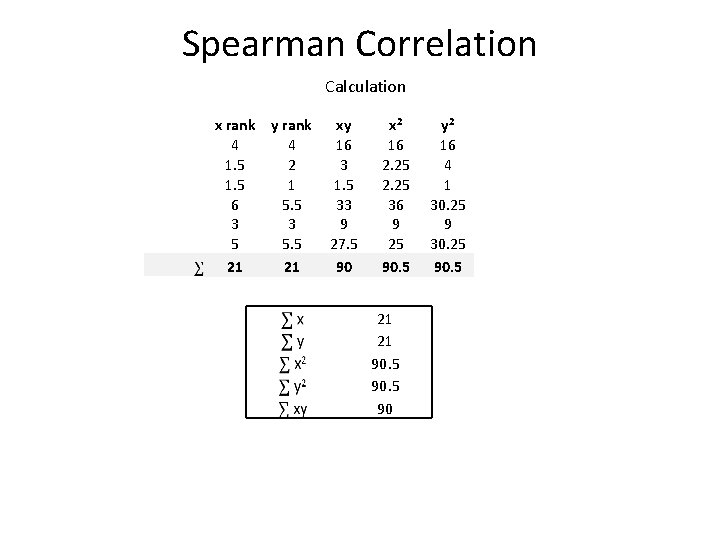
Spearman Correlation Calculation x rank y rank 4 4 1. 5 2 1. 5 1 6 5. 5 3 3 5 5. 5 21 21 xy 16 3 1. 5 33 9 27. 5 90 x 2 16 2. 25 36 9 25 90. 5 21 21 90. 5 90 y 2 16 4 1 30. 25 90. 5

Spearman Correlation Calculation 21 21 90. 5 90

Spearman Correlation Special Formula x rank y rank 4 4 1. 5 2 1. 5 1 6 5. 5 3 3 5 5. 5 D 0 0. 5 -0. 5 0 0. 5 D 2 0 0. 25 0 1

Spearman Correlation Special Formula x rank y rank 4 4 1. 5 2 1. 5 1 6 5. 5 3 3 5 5. 5 v. s. D 0 0. 5 -0. 5 0 0. 5 D 2 0 0. 25 0 1

Hypothesis testing with spearman • Same process as Pearson – (still using table B. 7)

Appendix E Mann - Whitney U-Test Wilcoxon signed-rank test Kruskal – Wallace Test Friedman Test

Mann - Whitney U-Test – Requirements • • – Hypotheses: • •

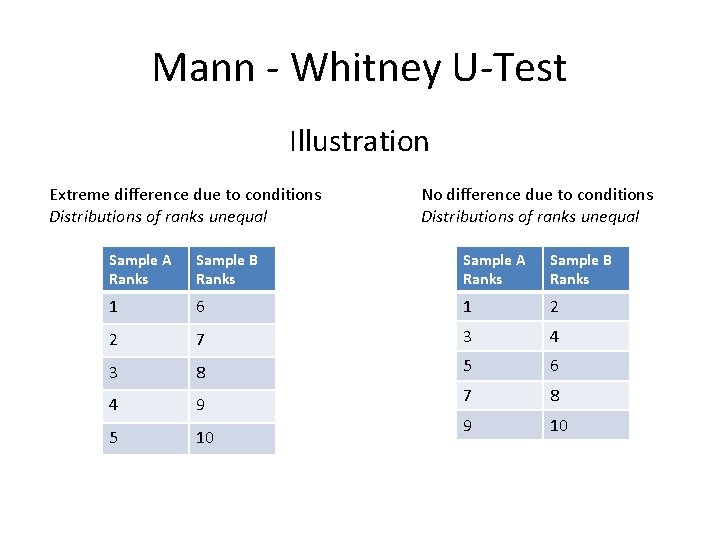
Mann - Whitney U-Test Illustration Extreme difference due to conditions Distributions of ranks unequal No difference due to conditions Distributions of ranks unequal Sample A Ranks Sample B Ranks 1 6 1 2 2 7 3 4 3 8 5 6 4 9 7 8 5 10 9 10

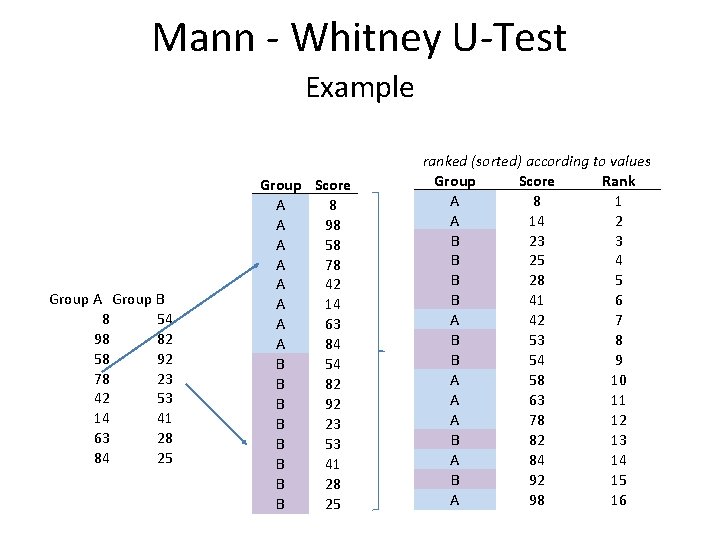
Mann - Whitney U-Test Example Group A Group B 8 54 98 82 58 92 78 23 42 53 14 41 63 28 84 25 Group Score A 8 A 98 A 58 A 78 A 42 A 14 A 63 A 84 B 54 B 82 B 92 B 23 B 53 B 41 B 28 B 25 ranked (sorted) according to values Group Score Rank A 8 1 A 14 2 B 23 3 B 25 4 B 28 5 B 41 6 A 42 7 B 53 8 B 54 9 A 58 10 A 63 11 A 78 12 B 82 13 A 84 14 B 92 15 A 98 16

Mann - Whitney U-Test Computing U by hand Group A A B B A A A B A Rank 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 A Ranks B Ranks 1 3 2 4 7 5 10 6 11 8 12 9 14 13 16 15 A Ranks 1 2 7 10 11 12 14 16 UA verify: U=27 0 0 4 6 6 6 7 8 37 8*8= 64 B Ranks 3 4 5 6 8 9 13 15 UB 37+27=64 2 2 3 3 6 7 27

Mann - Whitney U-Test Computing U via formula A Ranks B Ranks 1 3 2 4 7 5 10 6 11 8 12 9 14 13 16 15 73 63 U=27

Mann - Whitney U-Test Evaluating Significance with U H 0: H 1: U=27 alpha = 0. 05, 2 tails, df(8, 8) Critical value = 13 U > critical value, we fail to reject the null The ranks are equally distributed between samples

Mann - Whitney U-Test Write-Up The original scores were ranked ordered and a Mann-Whitney U-test was used to compare the ranks for the n = 8 participants in treatment A and the n = 8 participants in treatment B. The results indicate no significant difference between treatments, U = 27, p >. 05, with the sum of the ranks equal to 27 for treatment A and 37 for treatment B.

Mann - Whitney U-Test Evaluating Significance Using Normal Approximation With n>20, the MW-U distribution tends to approximate a normal shape, and so, can be evaluated using a z-score statistic as an alternative to the MW-U table. U=27 Note: n not > 20!

Mann - Whitney U-Test Evaluating Significance Using Normal Approximation alpha = 0. 05 2 tails Critical value: z = ± 1. 96 -0. 5251 is not in the critical region Fail to reject the null.

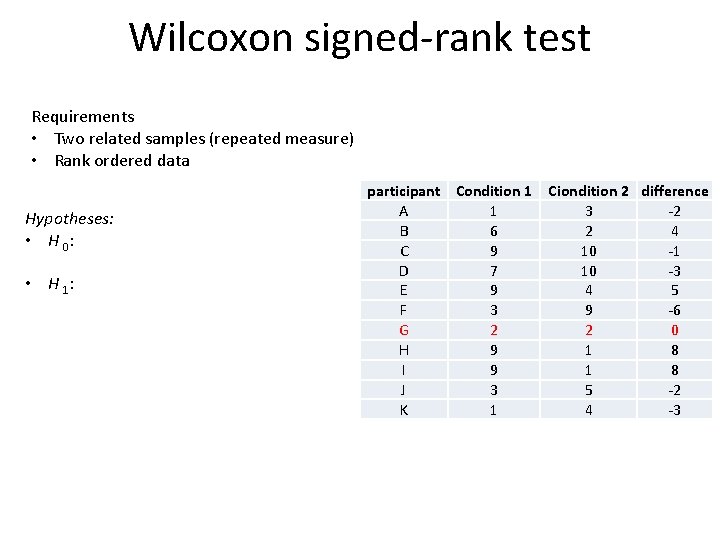
Wilcoxon signed-rank test Requirements • Two related samples (repeated measure) • Rank ordered data Hypotheses: • H 0: • H 1: participant Condition 1 A 1 B 6 C 9 D 7 E 9 F 3 G 2 H 9 I 9 J 3 K 1 Ciondition 2 difference 3 -2 2 4 10 -1 10 -3 4 5 9 -6 2 0 1 8 5 -2 4 -3

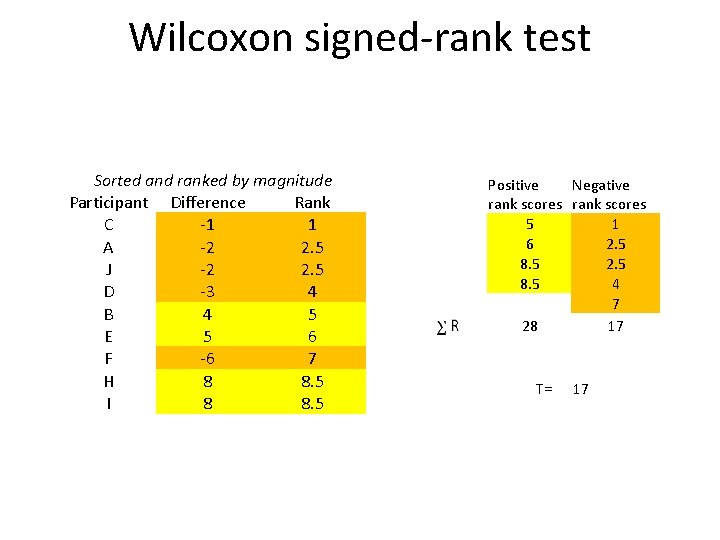
Wilcoxon signed-rank test Participant A B C D E F H I J K Difference -2 4 -1 -3 5 -6 8 8 -2 -3 Sorted and ranked by magnitude Participant Difference Rank C -1 1 A -2 2. 5 J -2 2. 5 D -3 4 B 4 5 E 5 6 F -6 7 H 8 8. 5 I 8 8. 5

Wilcoxon signed-rank test Sorted and ranked by magnitude Participant Difference Rank C -1 1 A -2 2. 5 J -2 2. 5 D -3 4 B 4 5 E 5 6 F -6 7 H 8 8. 5 I 8 8. 5 Positive Negative rank scores 5 1 6 2. 5 8. 5 4 7 28 17 T= 17

Wilcoxon signed-rank test n=10 alpha =. 05 two tales critical value = 8 T= 17 T obtained > critical value, fail to reject the null The difference scores are not systematically positive or systematically negative.

Wilcoxon signed-rank test Write up The 11 participants were rank ordered by the magnitude of their difference scores and a Wilcoxon T was used to evaluate the significance of the difference between treatments. One sample was removed due to having a zero difference score. The results indicate no significant difference, n = 10, T = 17, p <. 05, with the positive ranks totaling 28 and the negative ranks totaling 17.

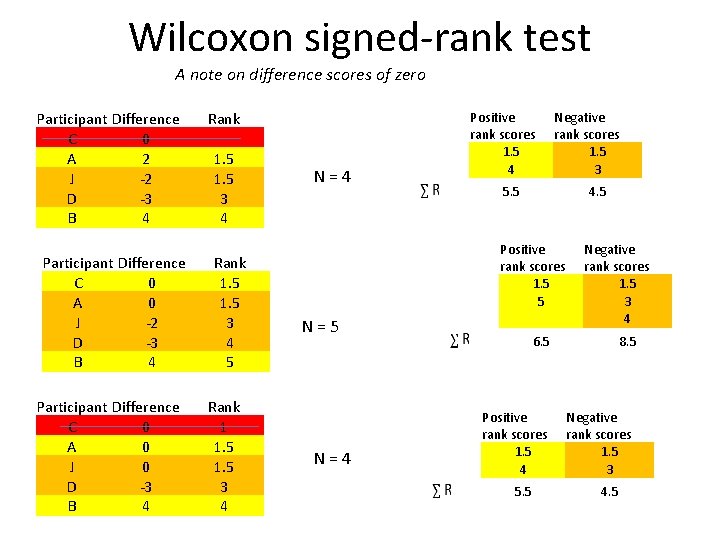
Wilcoxon signed-rank test A note on difference scores of zero Participant Difference C 0 A 2 J -2 D -3 B 4 Participant Difference C 0 A 0 J 0 D -3 B 4 Rank 1. 5 3 4 5 Rank 1 1. 5 3 4 N=4 Positive rank scores 1. 5 4 Negative rank scores 1. 5 3 5. 5 4. 5 Positive rank scores 1. 5 5 N=4 Negative rank scores 1. 5 3 4 6. 5 Positive rank scores 1. 5 4 5. 5 8. 5 Negative rank scores 1. 5 3 4. 5

Wilcoxon signed-rank test Evaluating Significance Using Normal Approximation T= 17 n= 10 Note: n not > 20!

Wilcoxon signed-rank test Evaluating Significance Using Normal Approximation alpha = 0. 05 2 tails Critical value: z = ± 1. 96 -0. 21847 is not in the critical region Fail to reject the null.

Interim Summary Calculation of Mann-Whitney or Wilcoxon is fair game on test. When to use Mann-Whitney or Wilcoxon • If data is already ordinal or ranked • If assumptions of parametric test are not met

Kruskal – Wallace Test • Alternative to independent measures ANOVA • Expands Mann – Whitney • Requirements • Null –

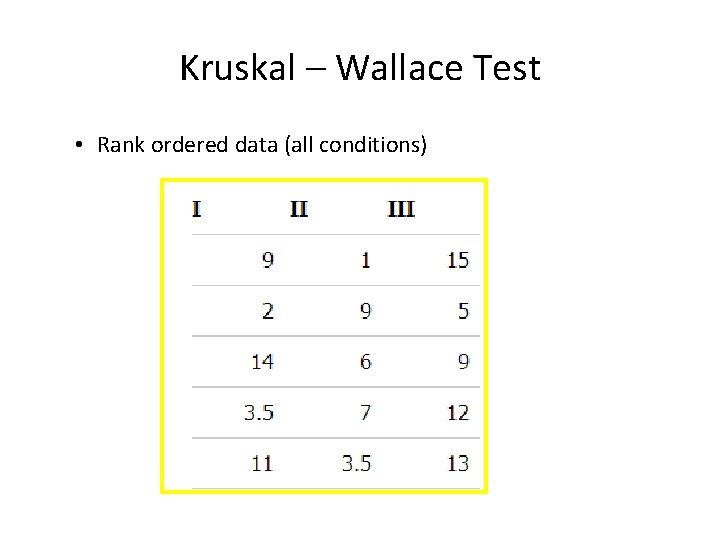
Kruskal – Wallace Test • Rank ordered data (all conditions)

Kruskal – Wallace Test For each treatment condition • n: n for each group • T: sum of ranks for each group Overall • N: Total participants Statistic identified with H Distribution approximates same distribution as chi-squared (i. e. use the chi squared table)

Friedman Test • Alternative to repeated measures ANOVA • Expands Wilcoxon test • Requirements • Null

Friedman Test • Rank ordered data (within each participant)

Friedman Test •

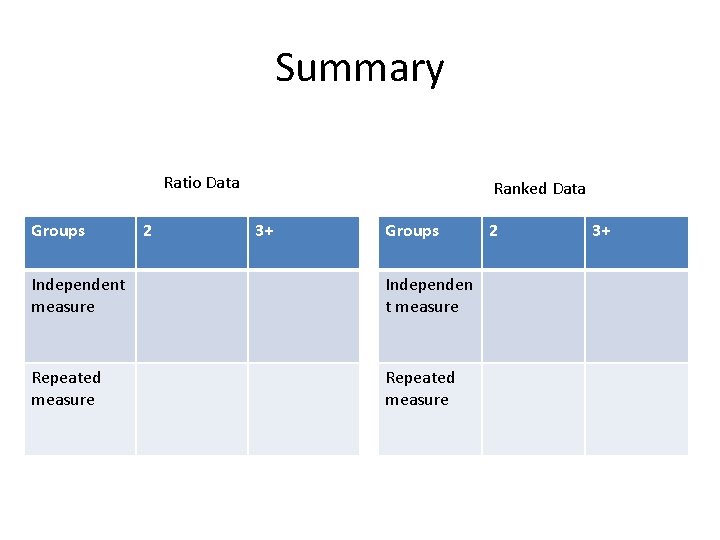
Summary Ratio Data Groups 2 Ranked Data 3+ Groups Independent measure Independen t measure Repeated measure 2 3+