Stats 346 3 Stats 848 3 Multivariate Data








































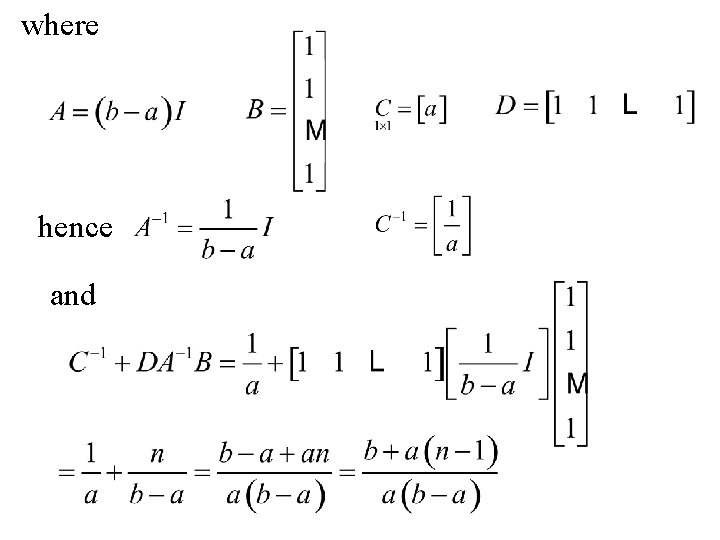

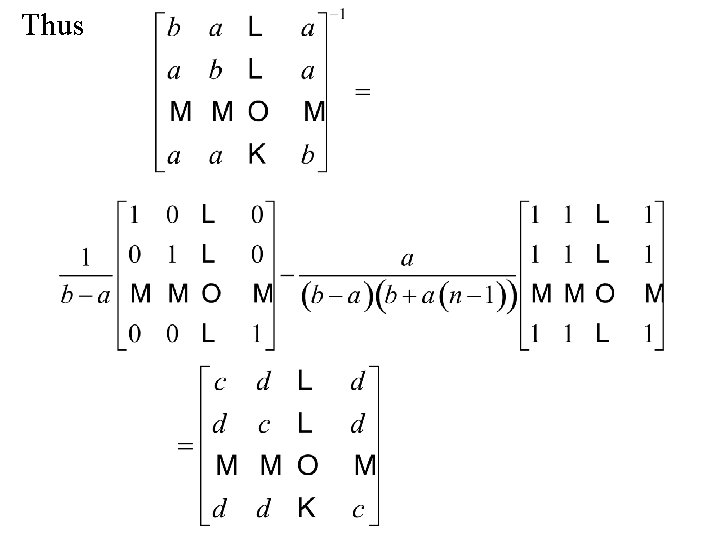
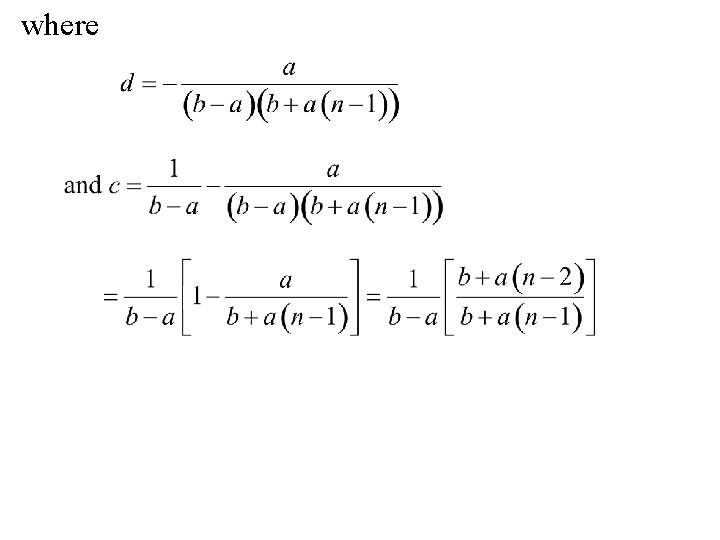
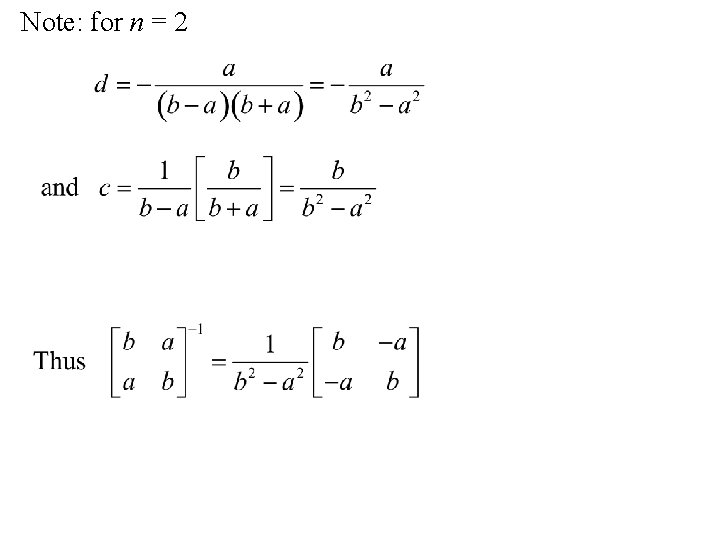
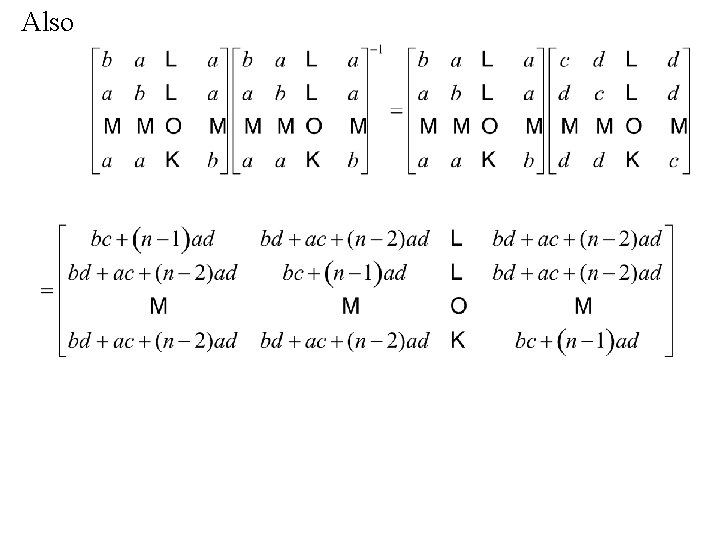
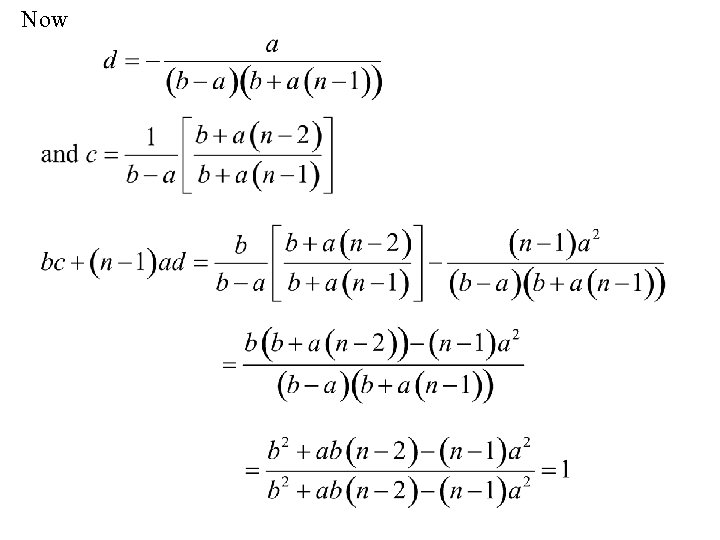




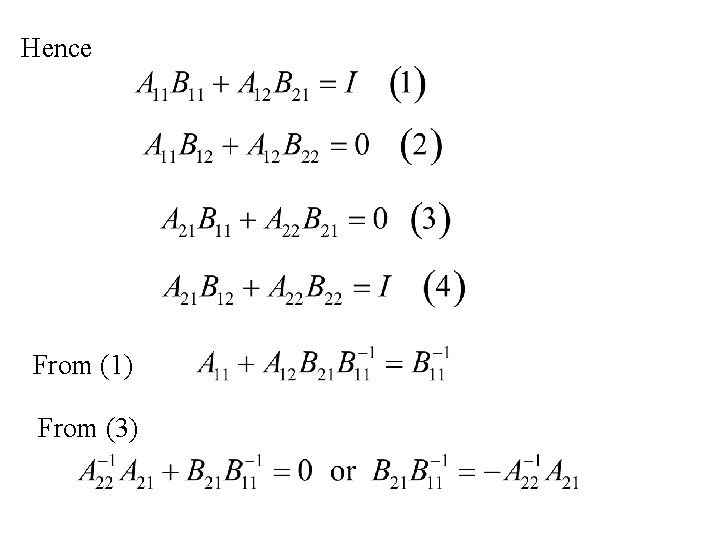

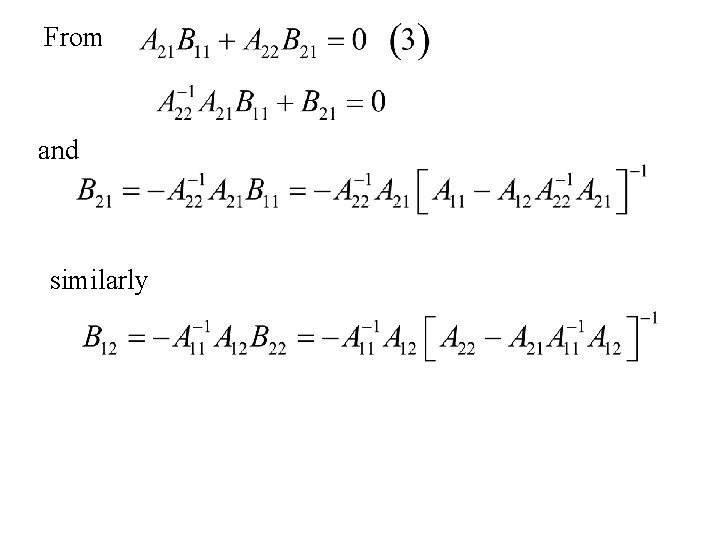

















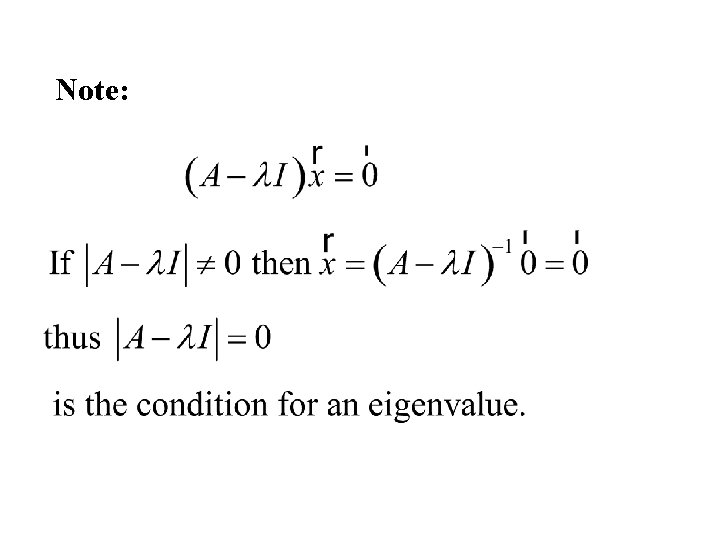





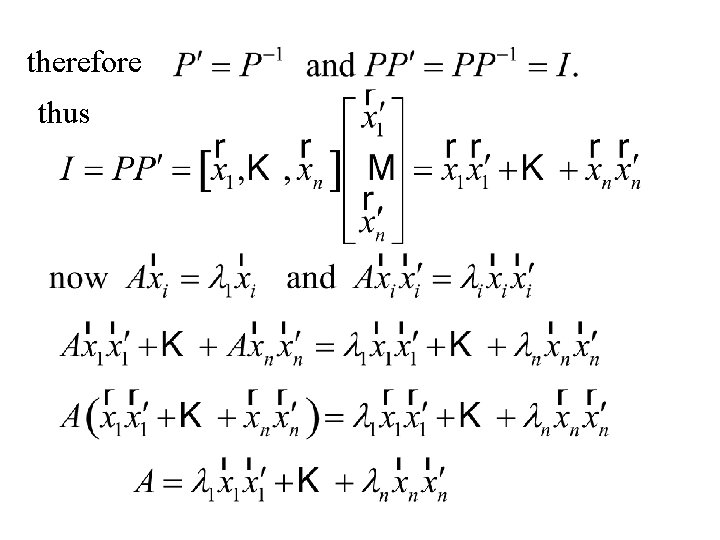
















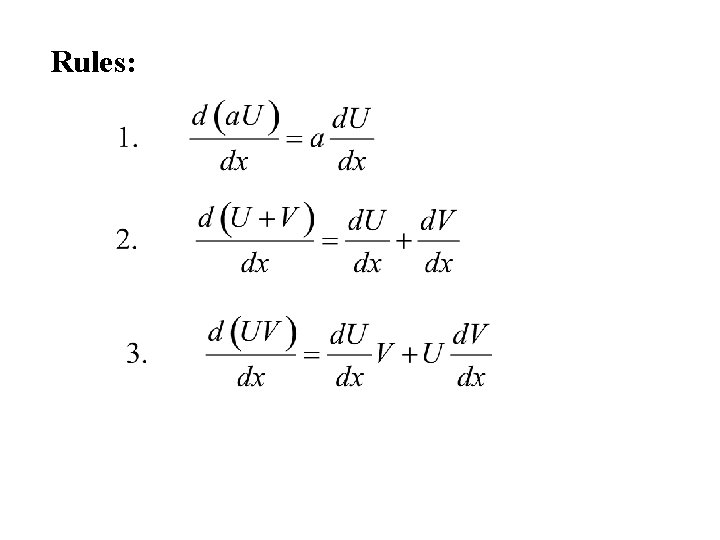
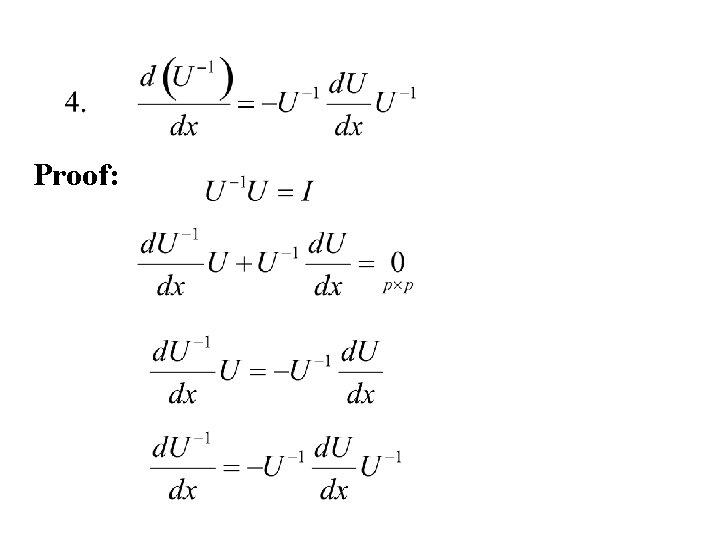
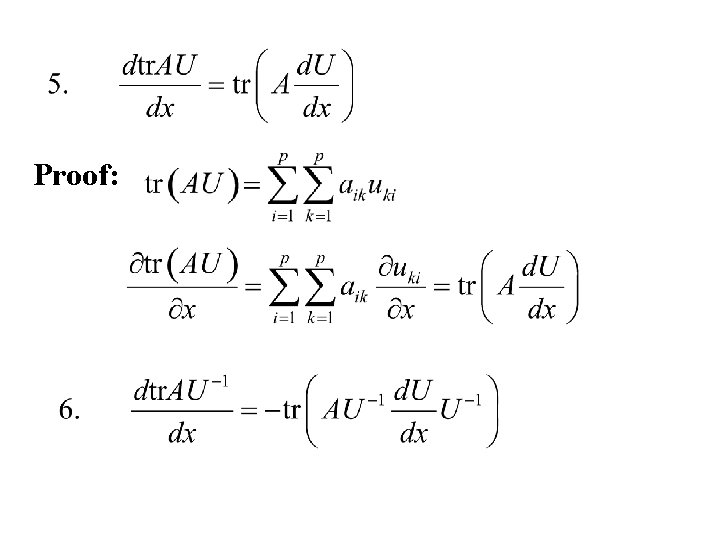







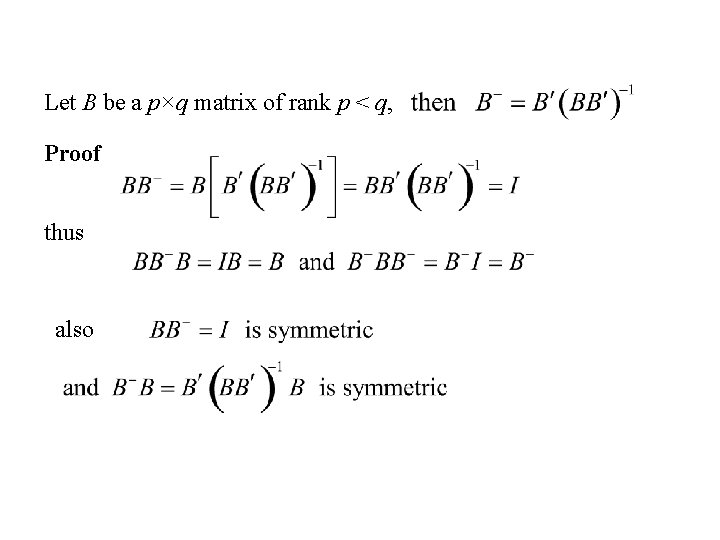
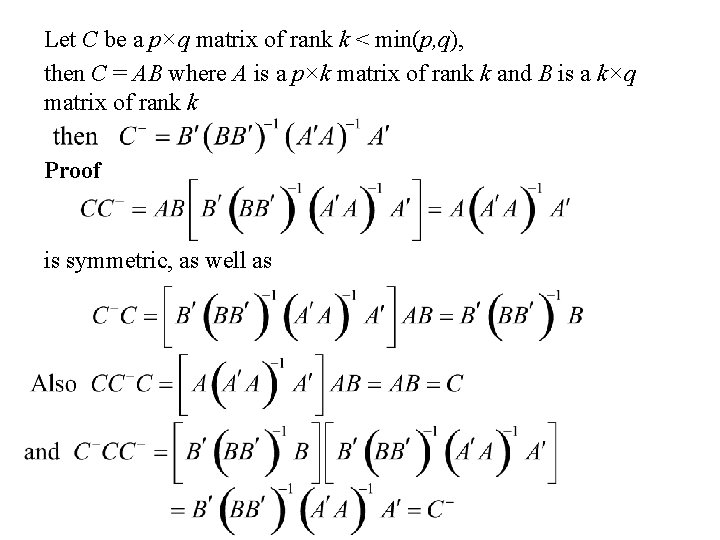

- Slides: 117

Stats 346. 3 Stats 848. 3 Multivariate Data Analysis

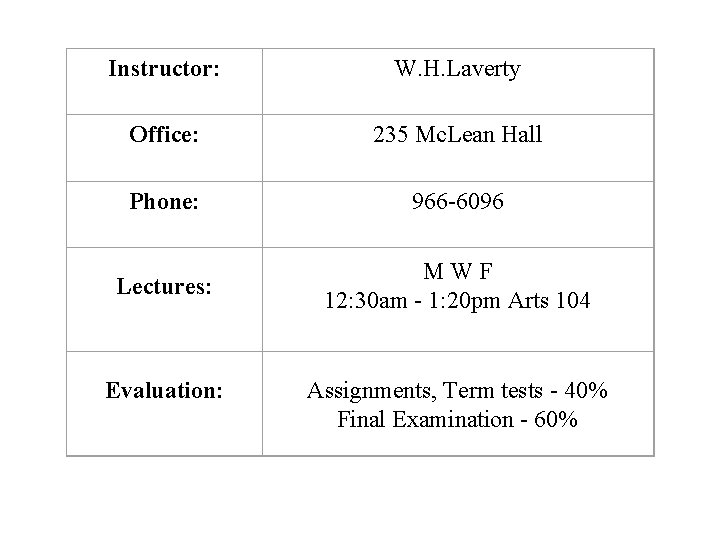
Instructor: W. H. Laverty Office: 235 Mc. Lean Hall Phone: 966 -6096 Lectures: MWF 12: 30 am - 1: 20 pm Arts 104 Evaluation: Assignments, Term tests - 40% Final Examination - 60%

Dates for midterm tests: 1. Friday, February 08 2. Friday, March 22 Each test and the Final Exam are Open Book Students are allowed to take in Notes, texts, formula sheets, calculators (laptop computers. )

Text: Stat 346 –Multivariate Statistical Methods – Donald Morrison Not Required - I will give a list of other useful texts that will be in the library

Bibliography 1. Cooley, W. W. , and Lohnes P. R. (1962). Multivariate Procedures for the Behavioural Sciences, Wiley, New York. 2. Fienberg, S. (1980), Analysis of Cross-Classified Data , MIT Press, Cambridge, Mass. 3. Fingelton, B. (1984), Models for Category Counts , Cambridge University Press. 4. Johnson, R. A. and Wichern D. W. Applied Multivariate Statistical Analysis , Prentice Hall. 5. Morrison, D. F. (1976), Multivariate Statistical Methods , Mc. Graw-Hill, New York. 6. Seal, H. (1968), Multivariate Statistical Analysis for Biologists , Metheun, London 7. Alan Agresti (1990) Categorical Data Analysis, Wiley, New York.

• The lectures will be given in Power Point • They are now posted on the Stats 346 web page

Course Outline

Introduction

Review of Linear Algebra and Matrix Analysis Chapter 2 Review of Linear Statistical Theory Chapter 1

Multivariate Normal distribution • Multivariate Data plots • Correlation - sample estimates and tests • Canonical Correlation Chapter 3

Mean Vectors and Covariance matrices • Single sample procedures • Two sample procedures • Profile Analysis Chapter 4

Multivariate Analysis of Variance (MANOVA) Chapter 5

Classification and Discrimination • Discriminant Analysis • Logistic Regression (if time permits) • Cluster Analysis Chapters 6

The structure of correlation • Principal Components Analysis (PCA) • Factor Analysis Chapter 9

Multivariate Multiple Regression (if time permits) References TBA

Discrete Multivariate Analysis (if time permits) References: TBA

Introduction

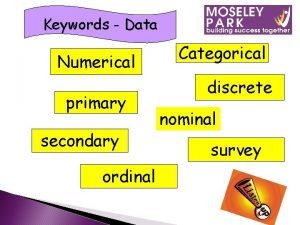
Multivariate Data • • • We have collected data for each case in the sample or population on not just one variable but on several variables – X 1, X 2, … Xp This is likely the situation – very rarely do you collect data on a single variable. The variables maybe 1. Discrete (Categorical) 2. Continuous (Numerical) • The variables may be 1. Dependent (Response variables) 2. Independent (Predictor variables)

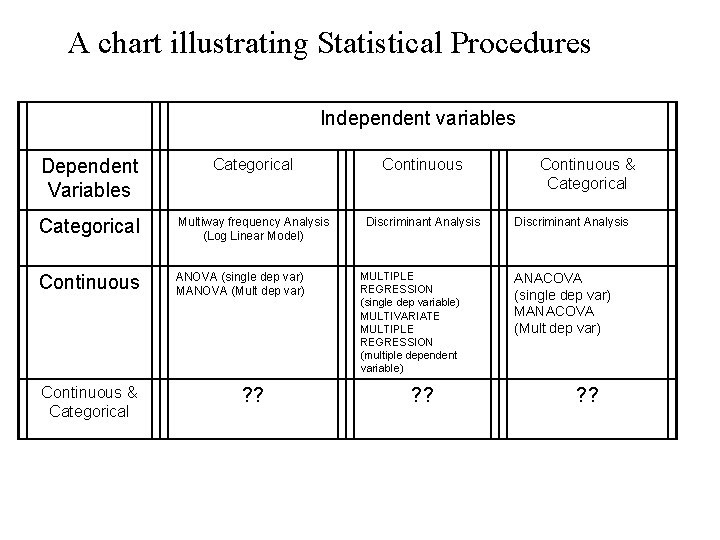
A chart illustrating Statistical Procedures Independent variables Dependent Variables Categorical Continuous Categorical Multiway frequency Analysis (Log Linear Model) Discriminant Analysis Continuous ANOVA (single dep var) MANOVA (Mult dep var) Continuous & Categorical ? ? MULTIPLE REGRESSION (single dep variable) MULTIVARIATE MULTIPLE REGRESSION (multiple dependent variable) ? ? Continuous & Categorical Discriminant Analysis ANACOVA (single dep var) MANACOVA (Mult dep var) ? ?

Multivariate Techniques can be classified as follows: 1. Techniques that are direct analogues of univariate procedures. • • • There are univariate techniques that are then generalized to the multivariate situarion e. g. The two independent sample t test, generalized to Hotelling’s T 2 test ANOVA (Analysis of Variance) generalized to MANOVA (Multivariate Analysis of Variance)

2. Techniques that are purely multivariate procedures. • • Correlation, Partial correlation, Multiple correlation, Canonical Correlation Principle component Analysis, Factor Analysis - These are techniques for studying complicated correlation structure amongst a collection of variables

3. Techniques for which a univariate procedures could exist but these techniques become much more interesting in the multivariate setting. • Cluster Analysis and Classification - • Here we try to identify subpopulations from the data Discriminant Analysis - In Discriminant Analysis, we attempt to use a collection of variables to identify the unknown population for which a case is a member

An Example: A survey was given to 132 students • Male=35, • Female=97 They rated, on a Likert scale • 1 to 5 • their agreement with each of 40 statements. All statements are related to the Meaning of Life

Questions and Statements

Statements - continued



Cluster Analysis of n = 132 university students using responses from Meaning of Life questionnaire (40 questions)

Discriminant Analysis of n = 132 university students into the three identified populations

A Review of Linear Algebra With some Additions

Matrix Algebra Definition An n × m matrix, A, is a rectangular array of elements n = # of columns m = # of rows dimensions = n × m

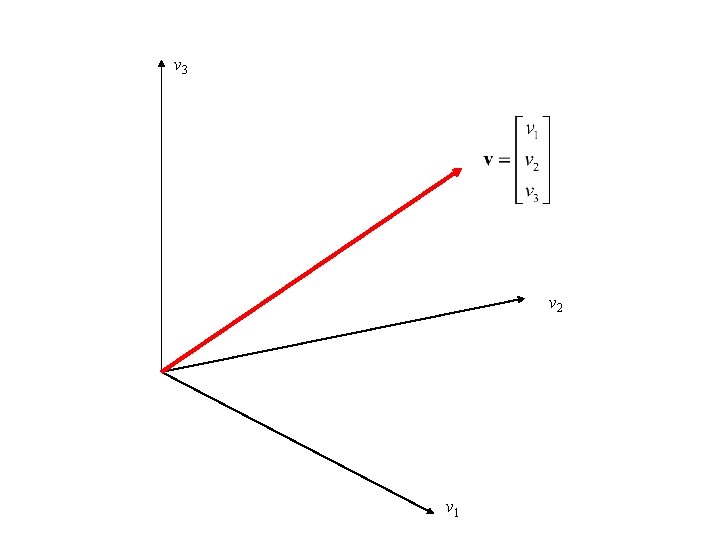
Definition A vector, v, of dimension n is an n × 1 matrix rectangular array of elements vectors will be column vectors (they may also be row vectors)

A vector, v, of dimension n can be thought a point in n dimensional space

v 3 v 2 v 1

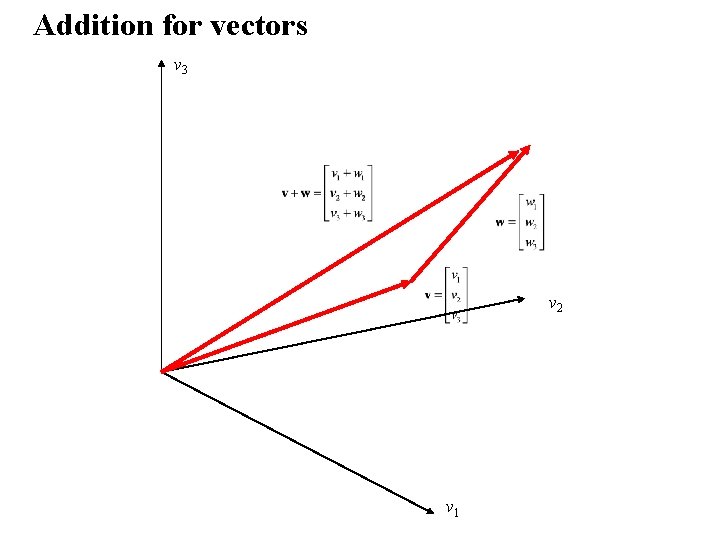
Matrix Operations Addition Let A = (aij) and B = (bij) denote two n × m matrices Then the sum, A + B, is the matrix The dimensions of A and B are required to be both n × m.

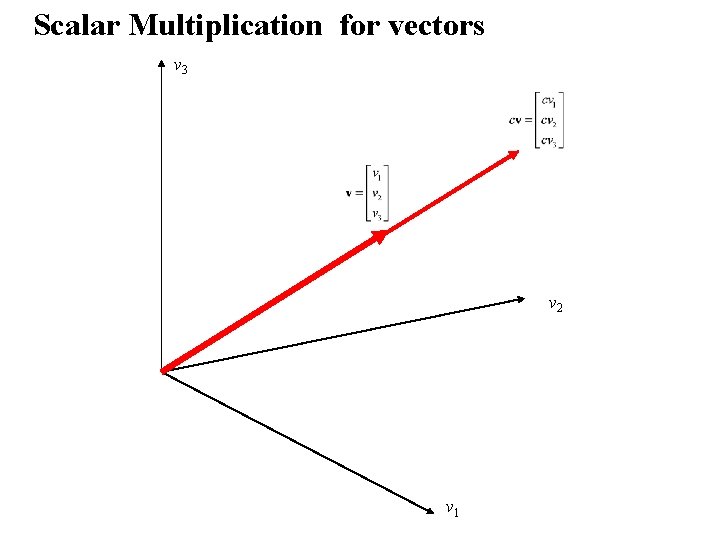
Scalar Multiplication Let A = (aij) denote an n × m matrix and let c be any scalar. Then c. A is the matrix

Addition for vectors v 3 v 2 v 1

Scalar Multiplication for vectors v 3 v 2 v 1

Matrix multiplication Let A = (aij) denote an n × m matrix and B = (bjl) denote an m × k matrix Then the n × k matrix C = (cil) where is called the product of A and B and is denoted by A∙B

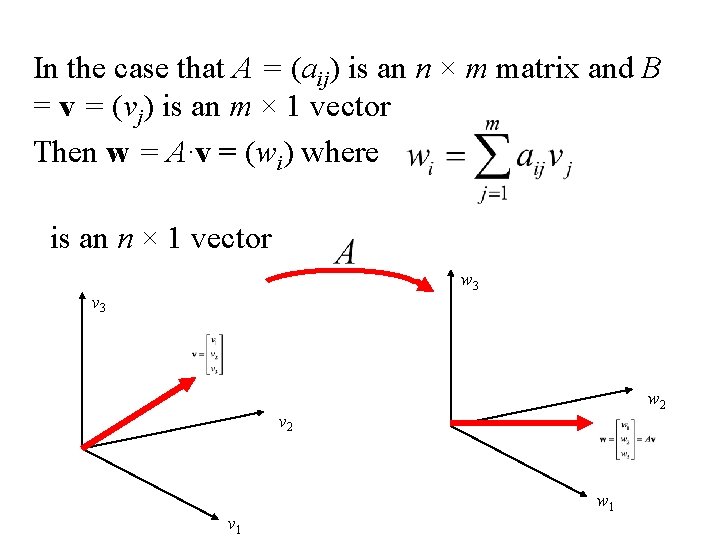
In the case that A = (aij) is an n × m matrix and B = v = (vj) is an m × 1 vector Then w = A∙v = (wi) where is an n × 1 vector w 3 v 3 w 2 v 1 w 1

Definition An n × n identity matrix, I, is the square matrix Note: 1. AI = A 2. IA = A.

Definition (The inverse of an n × n matrix) Let A denote the n × n matrix Let B denote an n × n matrix such that AB = BA = I, If the matrix B exists then A is called invertible Also B is called the inverse of A and is denoted by A-1

The Woodbury Theorem where the inverses

Proof: Let Then all we need to show is that H(A + BCD) = (A + BCD) H = I.


The Woodbury theorem can be used to find the inverse of some pattern matrices: Example: Find the inverse of the n × n matrix
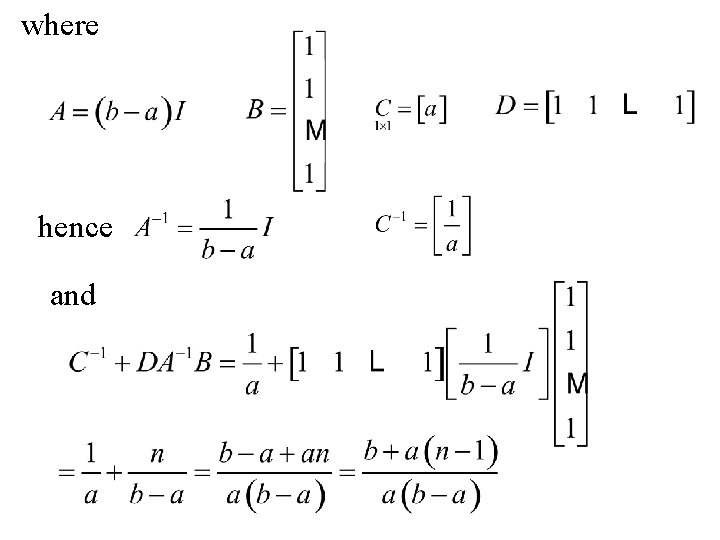
where hence and

Thus Now using the Woodbury theorem
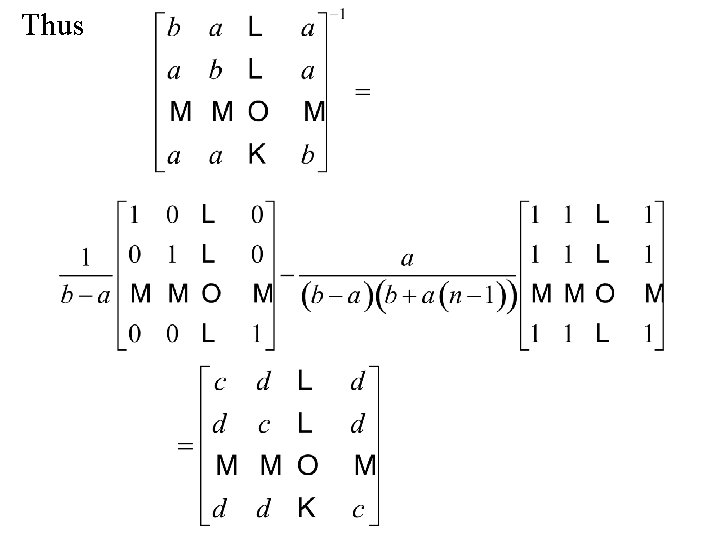
Thus
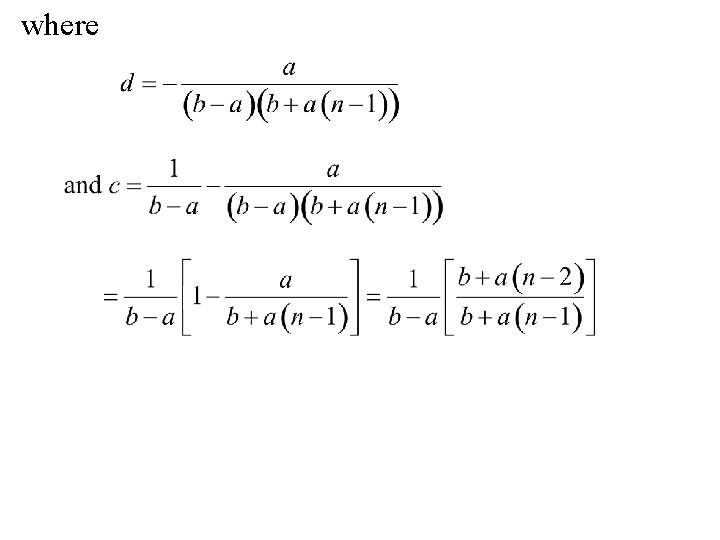
where
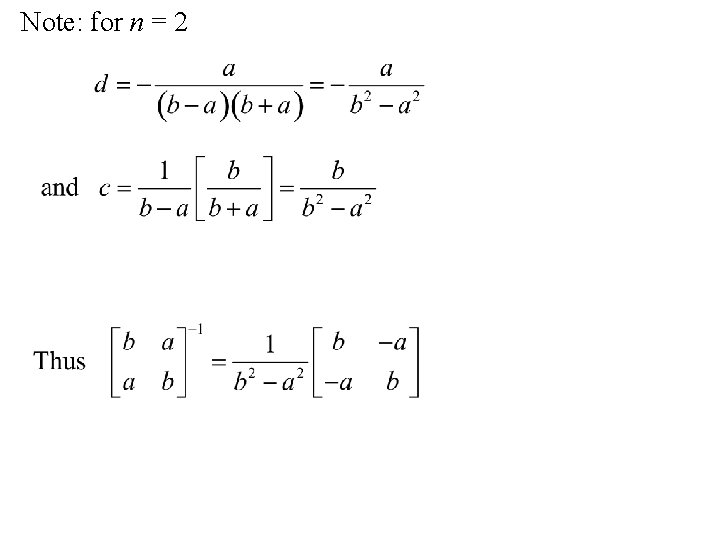
Note: for n = 2
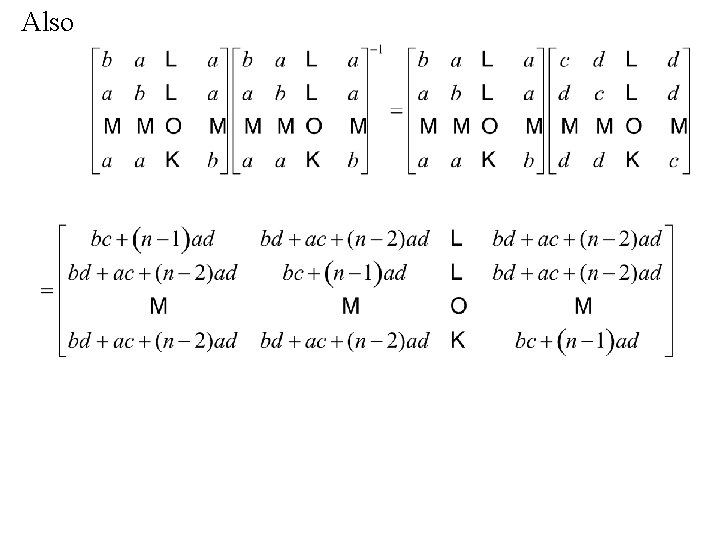
Also
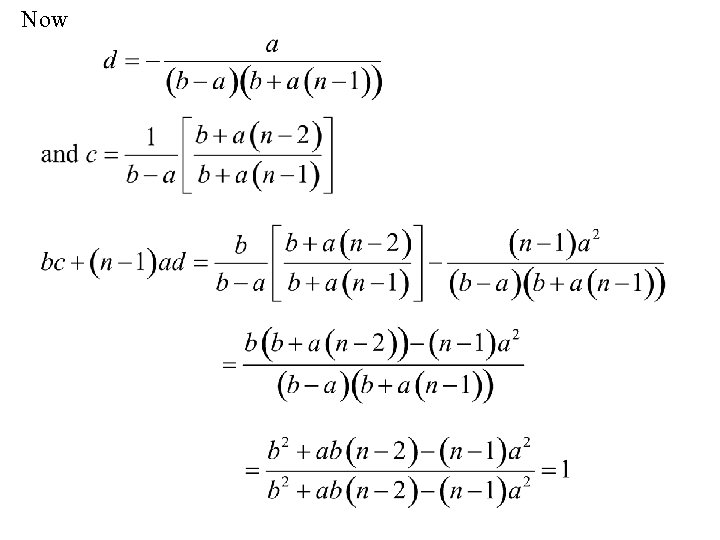
Now

and This verifies that we have calculated the inverse

Block Matrices Let the n × m matrix be partitioned into sub-matrices A 11, A 12, A 21, A 22, Similarly partition the m × k matrix

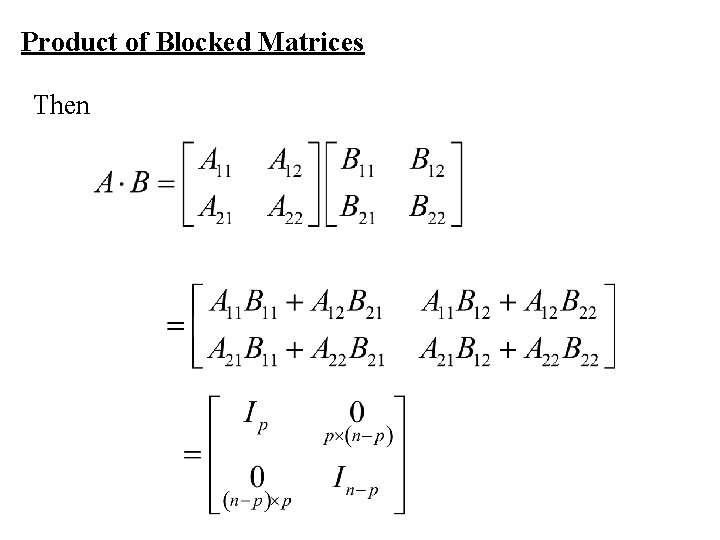
Product of Blocked Matrices Then

The Inverse of Blocked Matrices Let the n × n matrix be partitioned into sub-matrices A 11, A 12, A 21, A 22, Similarly partition the n × n matrix Suppose that B = A-1

Product of Blocked Matrices Then
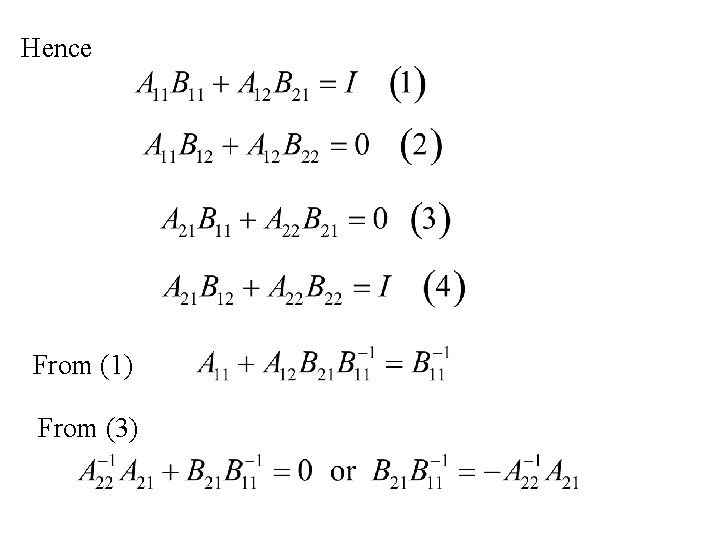
Hence From (1) From (3)

Hence or using the Woodbury Theorem Similarly
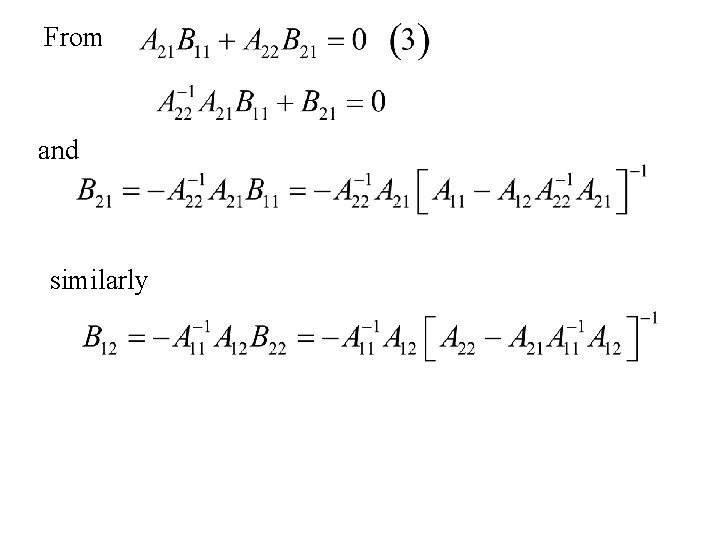
From and similarly

Summarizing Let Suppose that A-1 = B then

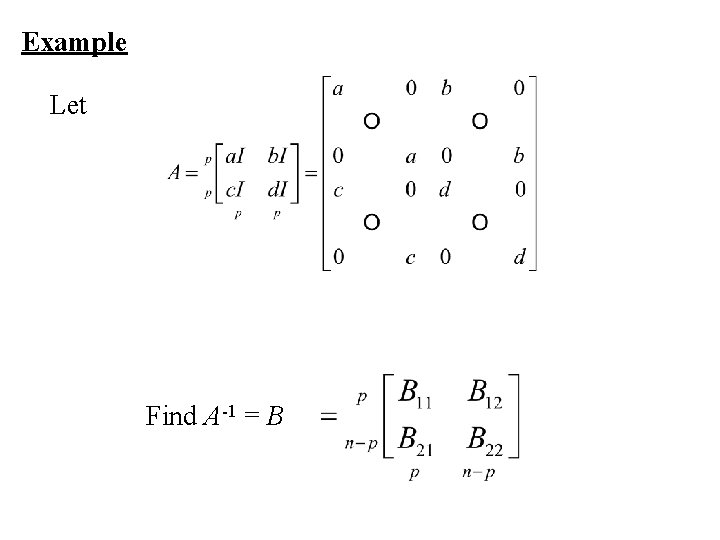
Example Let Find A-1 = B


The transpose of a matrix Consider the n × m matrix, A then the m × n matrix, (also denoted by AT) is called the transpose of A

Symmetric Matrices • An n × n matrix, A, is said to be symmetric if Note:

The trace and the determinant of a square matrix Let A denote then n × n matrix Then

also where

Some properties

Some additional Linear Algebra

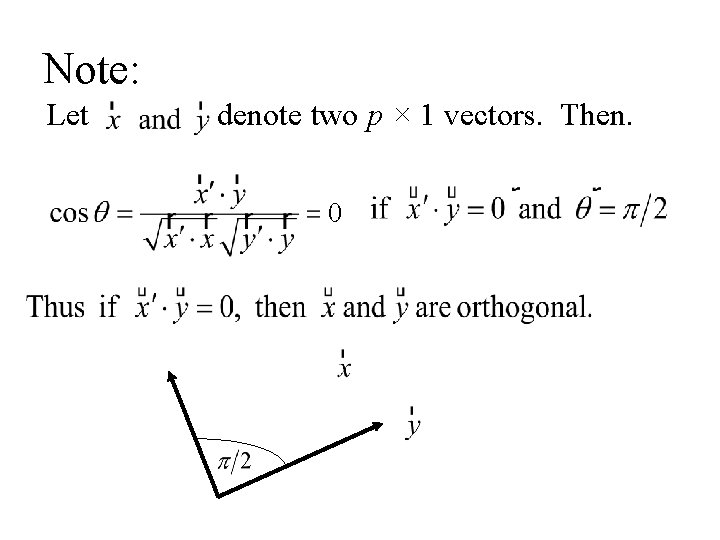
Inner product of vectors Let denote two p × 1 vectors. Then.

Note: Let denote two p × 1 vectors. Then.

Note: Let denote two p × 1 vectors. Then. 0

Special Types of Matrices 1. Orthogonal matrices – A matrix is orthogonal if P'P = PP' = I – In this cases P-1=P'. – Also the rows (columns) of P have length 1 and are orthogonal to each other

Suppose P is an orthogonal matrix then Let denote p × 1 vectors. Orthogonal transformation preserve length and angles – Rotations about the origin, Reflections

Example The following matrix P is orthogonal

Special Types of Matrices (continued) 2. Positive definite matrices – A symmetric matrix, A, is called positive definite if: – A symmetric matrix, A, is called positive semi definite if:

If the matrix A is positive definite then

Theorem The matrix A is positive definite if

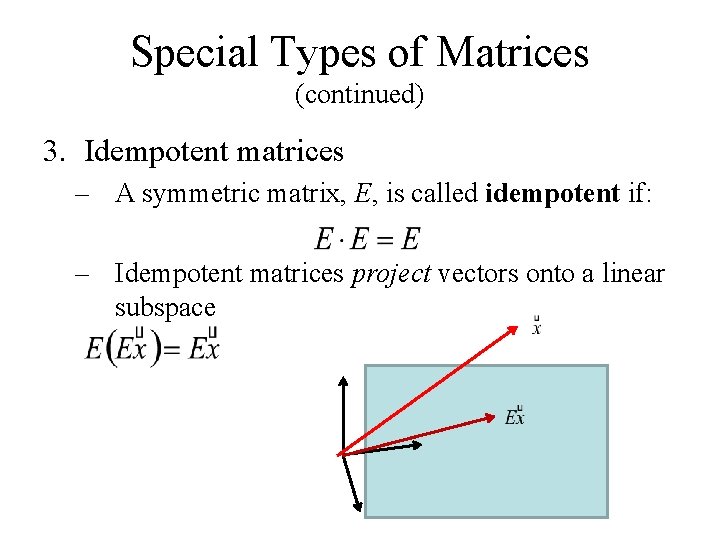
Special Types of Matrices (continued) 3. Idempotent matrices – A symmetric matrix, E, is called idempotent if: – Idempotent matrices project vectors onto a linear subspace

Definition Let A be an n × n matrix Let then l is called an eigenvalue of A and is called an eigenvector of A and
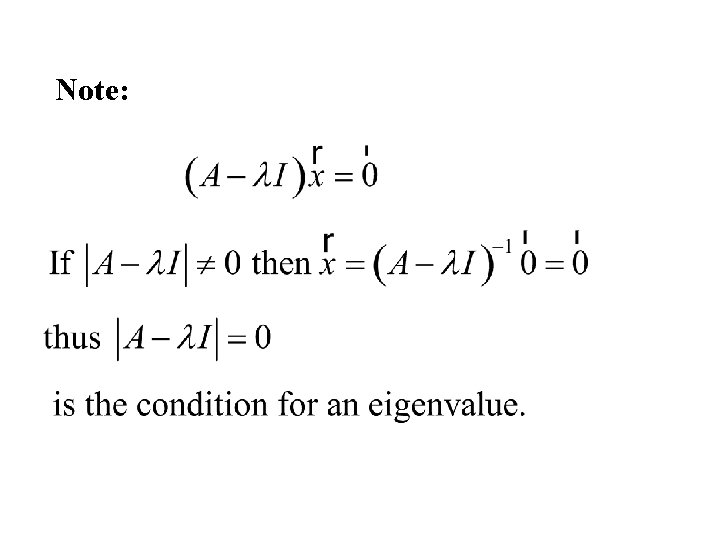
Note:

= polynomial of degree n in l. Hence there are n possible eigenvalues l 1, … , ln

Thereom If the matrix A is symmetric then the eigenvalues of A, l 1, … , ln, are real. Thereom If the matrix A is positive definite then the eigenvalues of A, l 1, … , ln, are positive. Proof A is positive definite if Let be an eigenvalue and corresponding eigenvector of A.

Thereom If the matrix A is symmetric and the eigenvalues of A are l 1, … , ln, with corresponding eigenvectors If li ≠ lj then Proof: Note

Thereom If the matrix A is symmetric with distinct eigenvalues, l 1, … , ln, with corresponding eigenvectors Assume

proof Note and P is called an orthogonal matrix
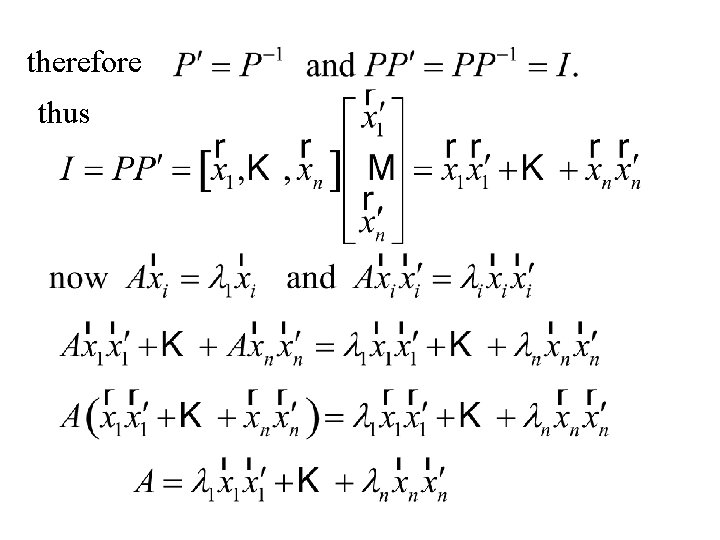
therefore thus

Comment The previous result is also true if the eigenvalues are not distinct. Namely if the matrix A is symmetric with eigenvalues, l 1, … , ln, with corresponding eigenvectors of unit length

An algorithm for computing eigenvectors, eigenvalues of positive definite matrices • Generally to compute eigenvalues of a matrix we need to first solve the equation for all values of l. – |A – l. I| = 0 (a polynomial of degree n in l) • Then solve the equation for the eigenvector

Recall that if A is positive definite then It can be shown that and that

Thus for large values of m The algorithim 1. Compute powers of A - A 2 , A 4 , A 8 , A 16 , . . . 2. Rescale (so that largest element is 1 (say)) 3. Continue until there is no change, The resulting matrix will be 4. Find 5. Find

To find 6. Repeat steps 1 to 5 with the above matrix to find 7. Continue to find

Example A=

Differentiation with respect to a vector, matrix

Differentiation with respect to a vector Let denote a p × 1 vector. Let function of the components of. denote a

Rules 1. Suppose

2. Suppose

Example 1. Determine when is a maximum or minimum. solution

2. Determine when is a maximum if Assume A is a positive definite matrix. solution l is the Lagrange multiplier. This shows that is an eigenvector of A. Thus is the eigenvector of A associated with the largest eigenvalue, l.

Differentiation with respect to a matrix Let X denote a q × p matrix. Let f (X) denote a function of the components of X then:

Example Let X denote a p × p matrix. Let f (X) = ln |X| Solution Note Xij are cofactors = (i, j)th element of X-1

Example Let X and A denote p × p matrices. Let f (X) = tr (AX) Solution

Differentiation of a matrix of functions Let U = (uij) denote a q × p matrix of functions of x then:
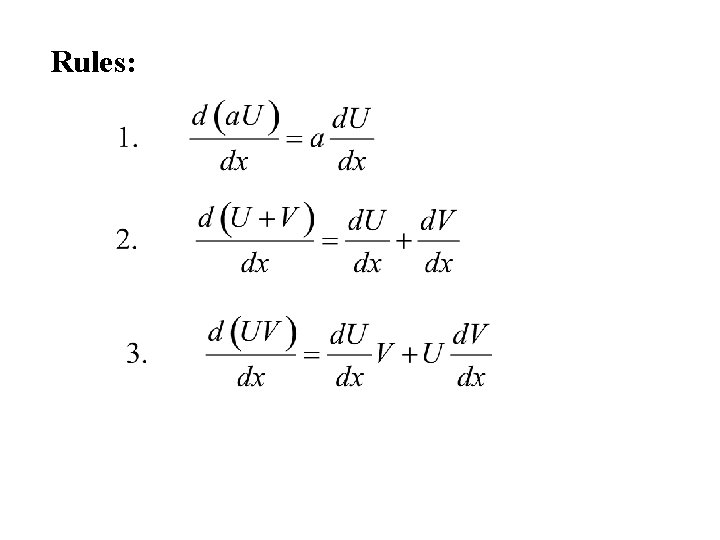
Rules:
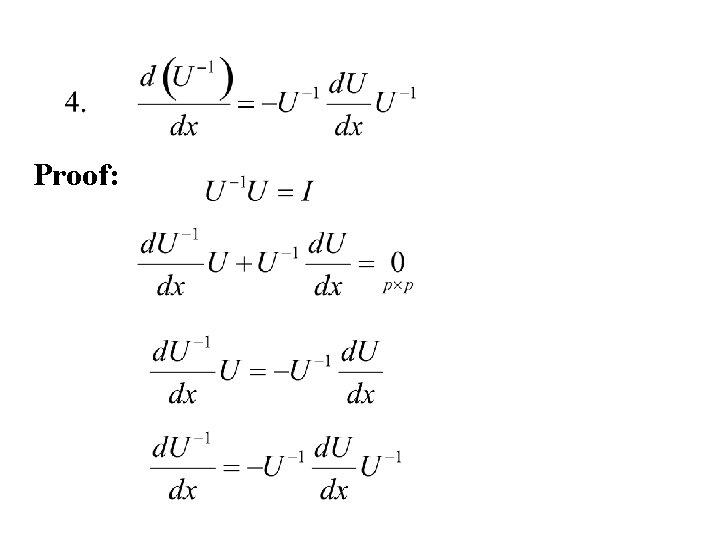
Proof:
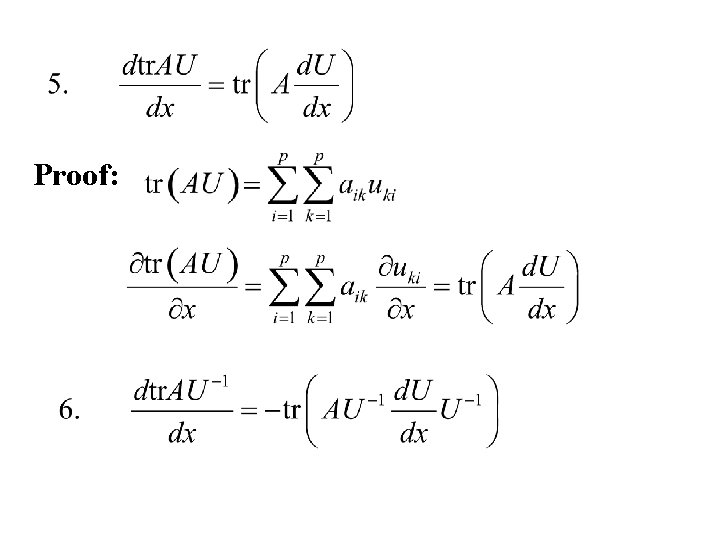
Proof:

Proof:

The Generalized Inverse of a matrix

Recall B (denoted by A-1) is called the inverse of A if AB = BA = I • A-1 does not exist for all matrices A • A-1 exists only if A is a square matrix and |A| ≠ 0 • If A-1 exists then the system of linear equations has a unique solution

Definition B (denoted by A-) is called the generalized inverse (Moore – Penrose inverse) of A if 1. ABA = A 2. BAB = B 3. (AB)' = AB 4. (BA)' = BA Note: A- is unique Proof: Let B 1 and B 2 satisfying 1. ABi. A = A 2. Bi. ABi = Bi 3. (ABi)' = ABi 4. (Bi. A)' = Bi. A

Hence B 1 = B 1 AB 2 AB 1 = B 1 (AB 2)'(AB 1) ' = B 1 B 2'A'B 1'A'= B 1 B 2'A' = B 1 AB 2 AB 2 = (B 1 A)(B 2 A)B 2 = (B 1 A)'(B 2 A)'B 2 = A'B 1'A'B 2 = A'B 2= (B 2 A)'B 2 = B 2 AB 2 = B 2 The general solution of a system of Equations The general solution where is arbitrary

Suppose a solution exists Let

Calculation of the Moore-Penrose g-inverse Let A be a p×q matrix of rank q < p, Proof thus also
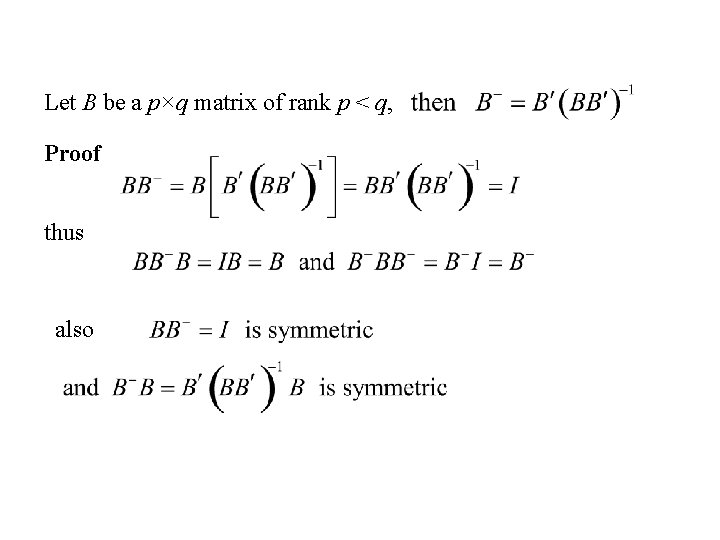
Let B be a p×q matrix of rank p < q, Proof thus also
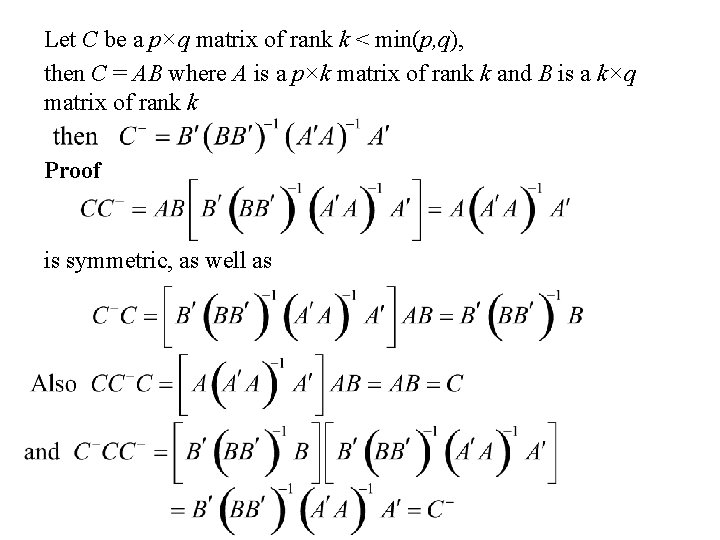
Let C be a p×q matrix of rank k < min(p, q), then C = AB where A is a p×k matrix of rank k and B is a k×q matrix of rank k Proof is symmetric, as well as

References 1. Matrix Algebra Useful for Statistics, Shayle R. Searle 2. Mathematical Tools for Applied Multivariate Analysis, J. Douglas Carroll, Paul E. Green
 Stats-346
Stats-346 848 932 2254
848 932 2254 16 9 in pixels
16 9 in pixels Ist 346
Ist 346 Byk 333
Byk 333 Cranial nerves 346
Cranial nerves 346 37.62 rounded to the nearest hundredth
37.62 rounded to the nearest hundredth Lei 11.346/2006
Lei 11.346/2006 625 to the nearest ten
625 to the nearest ten Rd 346 2011
Rd 346 2011 Ley 14 346
Ley 14 346 Cipher of 346
Cipher of 346 Differentialgleichung logistisches wachstum
Differentialgleichung logistisches wachstum Multivariate binomial distribution
Multivariate binomial distribution Multivariate pdf
Multivariate pdf What is multivariate analysis
What is multivariate analysis Linear regression spss interpretation
Linear regression spss interpretation Maximum likelihood function
Maximum likelihood function Maximum a posteriori estimation for multivariate gaussian
Maximum a posteriori estimation for multivariate gaussian Multivariate pdf
Multivariate pdf Bivariate vs multivariate
Bivariate vs multivariate Multiple variance analysis
Multiple variance analysis Manova with repeated measures
Manova with repeated measures Univariate vs multivariate logistic regression
Univariate vs multivariate logistic regression Multivariate methods in machine learning
Multivariate methods in machine learning Nature of multivariate analysis
Nature of multivariate analysis Multivariate verfahren psychologie
Multivariate verfahren psychologie Multivariate analysis of variance and covariance
Multivariate analysis of variance and covariance Univariate vs multivariate
Univariate vs multivariate A and b is
A and b is Advanced and multivariate statistical methods
Advanced and multivariate statistical methods Multivariate descriptive statistics
Multivariate descriptive statistics Multivariate analysis
Multivariate analysis Multivariate statistics for the environmental sciences
Multivariate statistics for the environmental sciences Multivariate statistical analysis
Multivariate statistical analysis Multivariate analysis
Multivariate analysis Multivariate histogram
Multivariate histogram Multivariate analysis
Multivariate analysis Multivariate pattern analysis
Multivariate pattern analysis Statistics complement rule
Statistics complement rule Experimental unit stats
Experimental unit stats Privisol
Privisol It&m stats
It&m stats Vampires prey on panama extreme language
Vampires prey on panama extreme language Stats p hat
Stats p hat Modality stats
Modality stats Chapter 24 paired samples and blocks
Chapter 24 paired samples and blocks When we take a census we attempt to collect data from
When we take a census we attempt to collect data from Chapter 7 ap stats review
Chapter 7 ap stats review Stats symbols
Stats symbols Mrs daniels ap stats
Mrs daniels ap stats Jared derksen
Jared derksen Stats refund
Stats refund Standard error of slope formula
Standard error of slope formula What are experimental units in stats
What are experimental units in stats Stats 330
Stats 330 Riak cs stats
Riak cs stats Parameter vs statistic definition
Parameter vs statistic definition Non fiction signposts
Non fiction signposts Stats$sql_summary
Stats$sql_summary Mcommerce stats
Mcommerce stats Stat 134
Stat 134 Mendeley stats
Mendeley stats Disjoint events
Disjoint events Ap stats experimental design
Ap stats experimental design Does the moon rotate
Does the moon rotate Stats canada
Stats canada Standard error of difference between two proportions
Standard error of difference between two proportions Ap stats chapter 17 sampling distribution models
Ap stats chapter 17 sampling distribution models Chapter 6 ap statistics test
Chapter 6 ap statistics test Ap stats chapter 16
Ap stats chapter 16 Stats tree diagram
Stats tree diagram Ap stats chapter 17 sampling distribution models
Ap stats chapter 17 sampling distribution models Questioning stance
Questioning stance Stats for beginners
Stats for beginners Tiger woods
Tiger woods Iqv stats calculator
Iqv stats calculator Ogive graph definition
Ogive graph definition Ap stats chapter 10 understanding randomness
Ap stats chapter 10 understanding randomness Ap stats chapter 14
Ap stats chapter 14 Stats
Stats Webmetrics integration
Webmetrics integration Stats 330
Stats 330 Statsmodels.stats.weightstats.ztest
Statsmodels.stats.weightstats.ztest My stats lab
My stats lab Stats
Stats In cc stats
In cc stats Combined standard deviation formula
Combined standard deviation formula Hurricane florence stats
Hurricane florence stats Time really
Time really Ap stats
Ap stats Statistics variance
Statistics variance Stats table psychology
Stats table psychology 3 big questions
3 big questions Numbers and stats
Numbers and stats Stats 361
Stats 361 Stats
Stats Example of testing hypothesis
Example of testing hypothesis Stats table psychology
Stats table psychology Dbms_stats.copy_table_stats
Dbms_stats.copy_table_stats Meg joseph
Meg joseph Ohio university stats
Ohio university stats Stats 330
Stats 330 Freesurfer roi
Freesurfer roi Stats
Stats Arl statistics instructions
Arl statistics instructions Usable data definition
Usable data definition Subjective data for fever
Subjective data for fever Spatial data and attribute data
Spatial data and attribute data Ukuran pemusatan data dan penyebaran data
Ukuran pemusatan data dan penyebaran data Data sekunder
Data sekunder Spatial data and attribute data
Spatial data and attribute data Validity of data collection
Validity of data collection Data-data monitoring lingkungan merupakan gambaran dari
Data-data monitoring lingkungan merupakan gambaran dari Difference between data guard and active data guard
Difference between data guard and active data guard What are secondary keywords
What are secondary keywords Respiration meaning in bengali
Respiration meaning in bengali Discrete vs continuous data
Discrete vs continuous data