Statistical ZeroKnowledge Arguments Statistically Hiding Commitments from Any

Statistical Zero-Knowledge Arguments & Statistically Hiding Commitments from Any One-Way Function Minh Nguyen Shien Jin Ong Salil Vadhan Harvard University Iftach Haitner Omer Reingold Weizmann Institute

Assumptions for Cryptography § One-way functions ) – Pseudorandom generators [Hastad-Impagliazzo-Levin-Luby 90]. – Pseudorandom functions & private-key cryptography [Goldreich-Goldwasser-Micali 84] – Commitment schemes [Naor 89]. – Zero-knowledge proofs for NP [Goldreich-Micali. Wigderson 86]. – Digital signatures [Rompel 90]. § Almost all cryptographic tasks ) one-way functions. [Impagliazzo-Luby 89, Ostrovsky-Wigderson 93] § Some tasks not “black-box reducible” to one-way fns. – Public-key encryption [Impagliazzo-Rudich 89]

Main Results One-Way Functions ) Statistical ZK Arguments for NP & Statistically Hiding Commitments – Resolves an open problem posed by [Naor-Ostrovsky-Venkatesan-Yung 92]. – OWF implied by commitments & ZK for hard-on-avg problems [Impagliazzo-Luby 89, Ostrovsky-Wigderson 93]. – Key to unconditional results about ZK Arguments [Ong-Vadhan 07].

outline § Introduction § Commitments & ZK § Constructions from OWF with structure § Construction from any OWF § ZK ´ “Instance-Dependent” Commitments § Open Problems

outline § Introduction § Commitments & ZK § Constructions from OWF with structure § Construction from any OWF § ZK ´ “Instance-Dependent” Commitments § Open Problems

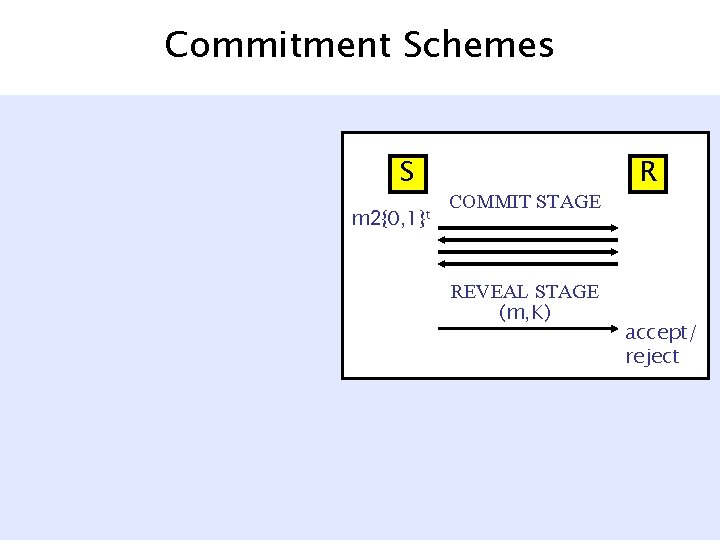
Commitment Schemes S m 2{0, 1}t COMMIT STAGE REVEAL STAGE (m, K) R accept/ reject

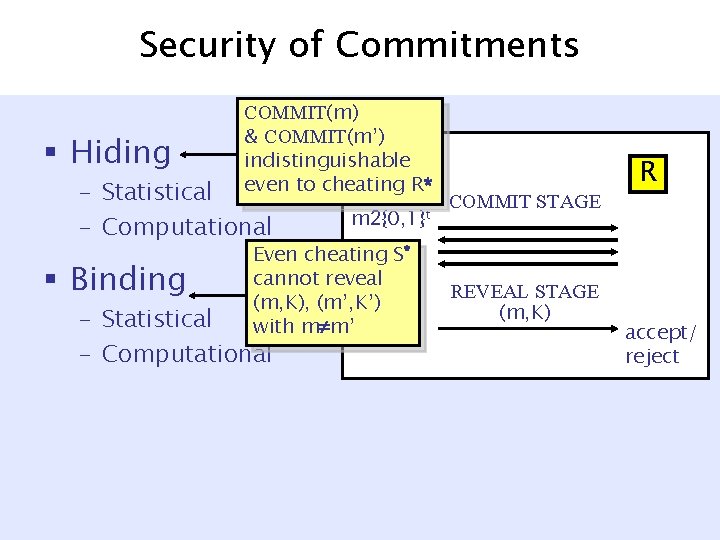
Security of Commitments § Hiding COMMIT(m) & COMMIT(m’) indistinguishable S even to cheating R* – Statistical – Computational § Binding m 2{0, 1}t Even cheating S* cannot reveal (m, K), (m’, K’) with m m’ – Statistical – Computational COMMIT STAGE REVEAL STAGE (m, K) R accept/ reject

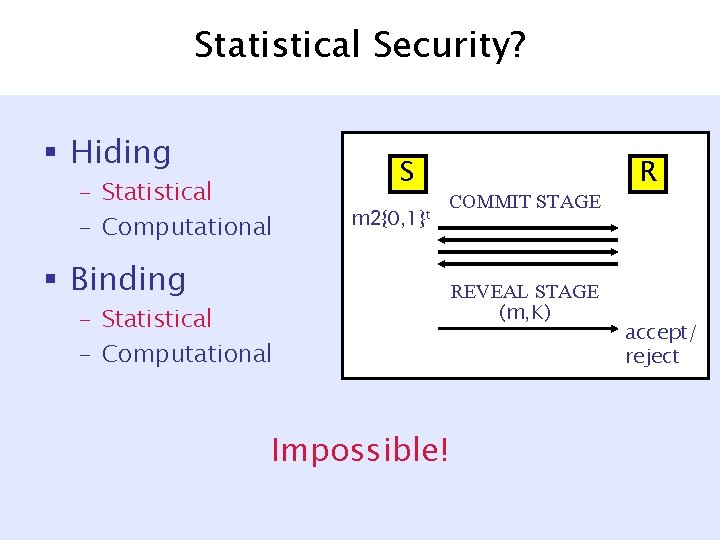
Statistical Security? § Hiding – Statistical – Computational S m 2{0, 1}t COMMIT STAGE § Binding – Statistical – Computational Impossible! REVEAL STAGE (m, K) R accept/ reject

Statistical Binding § Hiding – Statistical – Computational § Binding – Statistical – Computational S m 2{0, 1}t COMMIT STAGE REVEAL STAGE (m, K) Thm [HILL 90, Naor 91]: One-way functions ) Statistically Binding Commitments R accept/ reject

Statistical Hiding § Hiding – Statistical – Computational § Binding – Statistical – Computational S m 2{0, 1}t COMMIT STAGE REVEAL STAGE (m, K) This work: One-way functions ) Statistically Hiding Commitments R accept/ reject

Benefit of Statistical Hiding In most protocols that use commitments: § Binding only required during protocol execution – Depends on adversary’s current capabilities – Safe to be computational § Hiding may matter long after execution – Adversary may gain computational resources – Hardness assumption may be broken – Statistical hiding ) “everlasting secrecy”

Example: Zero Knowledge for NP [Goldreich-Micali-Wigderson 86] Hiding ) Zero Knowledge – Verifier learns nothing other than x 2 L Binding ) Soundness – Prover cannot convince verifier if x L Corollary: One-Way Functions ) Statistical Zero Knowledge Arguments for NP [Brassard-Chaum-Crepeau 88] P 6 1 2 3 5 4 (1, 4) V

Complexity of Statistically Hiding Commitments number-theoretic assumptions [GMR, BKK] claw-free perm [BCC] stat. hiding commitments ] [GK [GM R, Da mg ard [NY] ] collision-resistant hash functions

Complexity of Statistically Hiding Commitments ] [GK claw-free perm regular OWF VY ] 92 [NY] KK M S 05 ] NO [ one-way perm stat. hiding commitments H [GMR, BKK] [BCC] [H number-theoretic assumptions collision-resistant hash functions

Complexity of Statistically Hiding Commitments ] [GK claw-free perm VY ] 92 05 ] NO H K [H OR W TH IS regular OWF one-way function [NY] KK [ one-way perm stat. hiding commitments S [GMR, BKK] [BCC] M number-theoretic assumptions collision-resistant hash functions

Overview of the construction stat hiding One-way “ 1 -out-of-2 function [NOV 06] [HR 07] binding” stat hiding comp binding

outline § Introduction § Commitments & ZK § Constructions from OWF with structure § Construction from any OWF § ZK ´ “Instance-Dependent” Commitments § Open Problems

Structured One-Way Functions § f : {0, 1}n! {0, 1}n is one-way function if: – Computable in poly-time. – If xÃ{0, 1}n, no poly-time algorithm can find a preimage of f(x) w/nonneg. prob. § Regular OWF: f-1(y) same size for all y 2 f({0, 1}n). § One-Way Permutation: f a permutation.

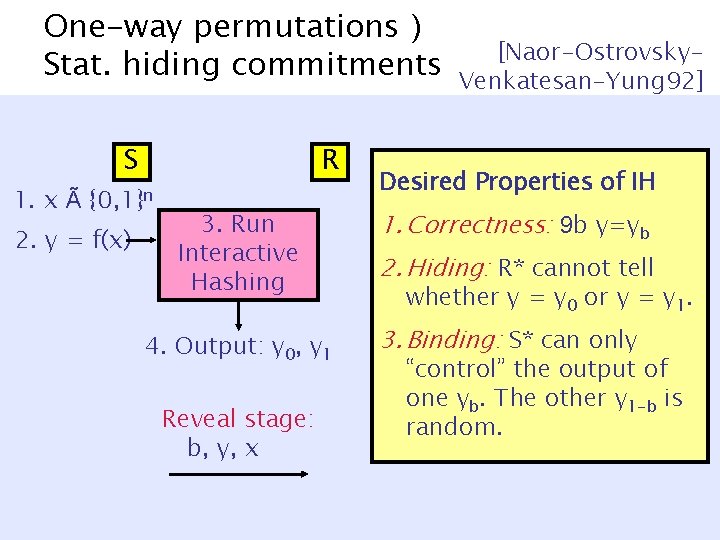
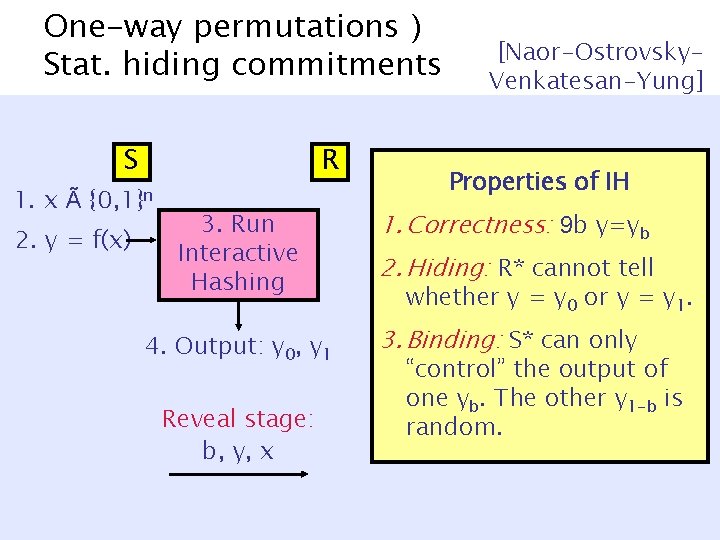
One-way permutations ) Stat. hiding commitments S 1. x à R {0, 1}n 2. y = f(x) [Naor-Ostrovsky. Venkatesan-Yung 92] Desired Properties of IH 3. Run Interactive Hashing 1. Correctness: 9 b y=yb 4. Output: y 0, y 1 3. Binding: S* can only Reveal stage: b, y, x 2. Hiding: R* cannot tell whether y = y 0 or y = y 1. “control” the output of one yb. The other y 1 -b is random.

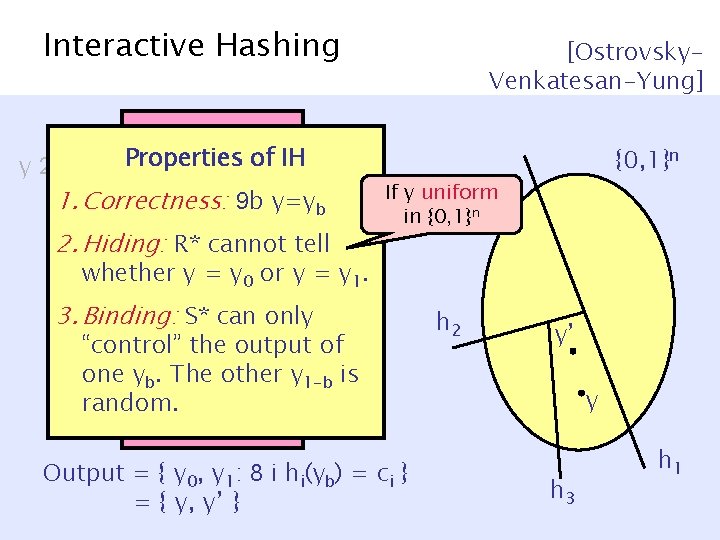
Interactive Hashing y 2 {0, 1}n S [Ostrovsky. Venkatesan-Yung] 3. Run Interactive Hashing h 1 {0, 1}n R c 1 = h 1(y) … hn-1 h 2 y’ y cn-1 = hn-1(y) Output = { y 0, y 1: 8 i hi(yb) = ci } = { y, y’ } h 3 h 1

Interactive Hashing y 2 3. Run Interactive of {0, 1}n Properties Hashing IH 1. Correctness: h 9 b y=yb S [Ostrovsky. Venkatesan-Yung] 1 R 2. Hiding: R* cannot tell {0, 1}n If y uniform in {0, 1}n … c 1 y==h 1 y(y)or y = y. whether 0 1 3. Binding: S* can only “control” the output of h one yb. Then-1 other y 1 -b is random. cn-1 = hn-1(y) Output = { y 0, y 1: 8 i hi(yb) = ci } = { y, y’ } h 2 y’ y h 3 h 1

One-way permutations ) Stat. hiding commitments S 1. x à R {0, 1}n 2. y = f(x) [Naor-Ostrovsky. Venkatesan-Yung] Properties of IH 3. Run Interactive Hashing 1. Correctness: 9 b y=yb 4. Output: y 0, y 1 3. Binding: S* can only Reveal stage: b, y, x 2. Hiding: R* cannot tell whether y = y 0 or y = y 1. “control” the output of one yb. The other y 1 -b is random.

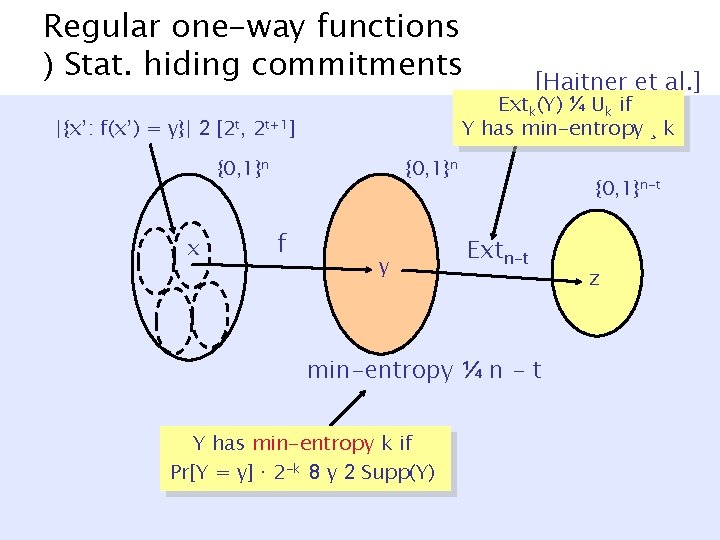
Regular one-way functions ) Stat. hiding commitments Extk(Y) ¼ Uk if Y has min-entropy ¸ k |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n x [Haitner et al. ] {0, 1}n f y {0, 1}n-t Extn-t min-entropy ¼ n - t Y has min-entropy k if Pr[Y = y] · 2 -k 8 y 2 Supp(Y) z

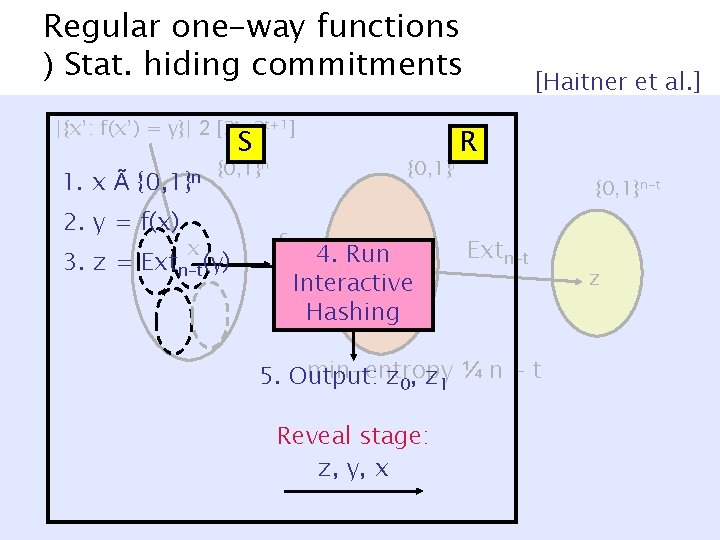
Regular one-way functions ) Stat. hiding commitments |{x’: f(x’) = y}| 2 [2 t, 2 t+1] S 1. x à {0, 1}n 2. y = f(x) x {0, 1}n 3. z = Extn-t(y) {0, 1}l f 4. Runy Interactive Hashing [Haitner et al. ] R {0, 1}n-t Extn-t min-entropy 5. Output: z 0, z 1 ¼ n - t Reveal stage: z, y, x z

Regular one-way functions ) Stat. hiding commitments [Haitner et al. ] |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n x {0, 1}l f y {0, 1}n-t Extn-t z min-entropy ¼ n - t Hiding: When x à {0, 1}n, z = Ext(f(x)) is close to uniform.

Regular one-way functions ) Stat. hiding commitments [Haitner et al. ] |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n x {0, 1}l f y {0, 1}n-t Extn-t z’ z ¢ 2 n-t Binding: Inverting Extn-t±f for ¢ 2 n-t strings in Z space ) Inverting f for ¢ 2 n-t¢ 2 t = ¢ 2 n strings in X space.

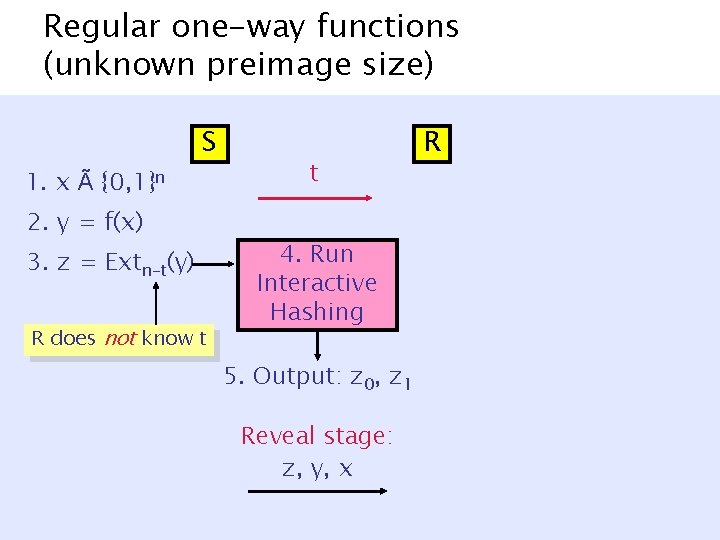
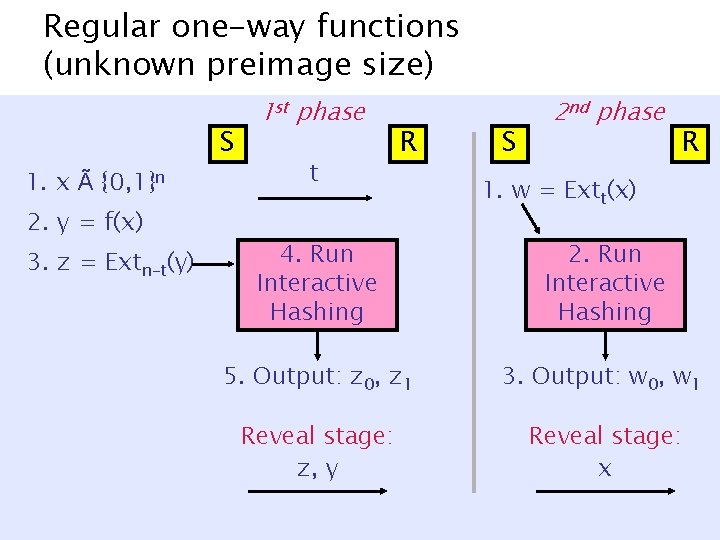
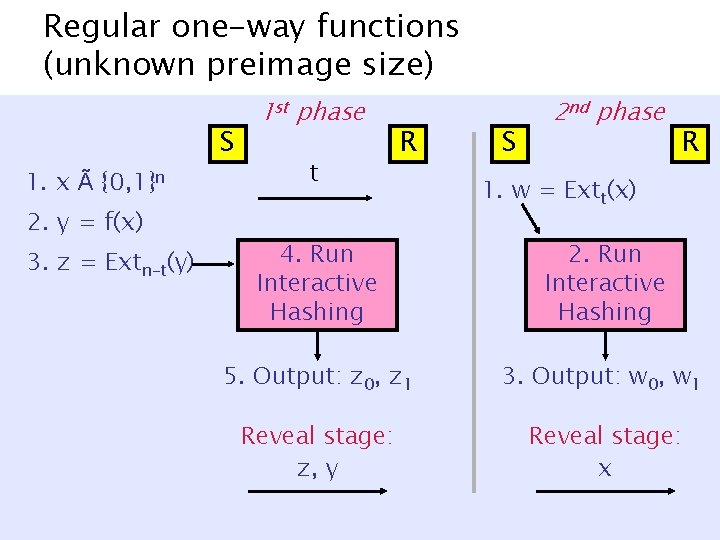
Regular one-way functions (unknown preimage size) S 1. x à {0, 1}n 2. y = f(x) 3. z = Extn-t(y) R does not know t t 4. Run Interactive Hashing 5. Output: z 0, z 1 Reveal stage: z, y, x R

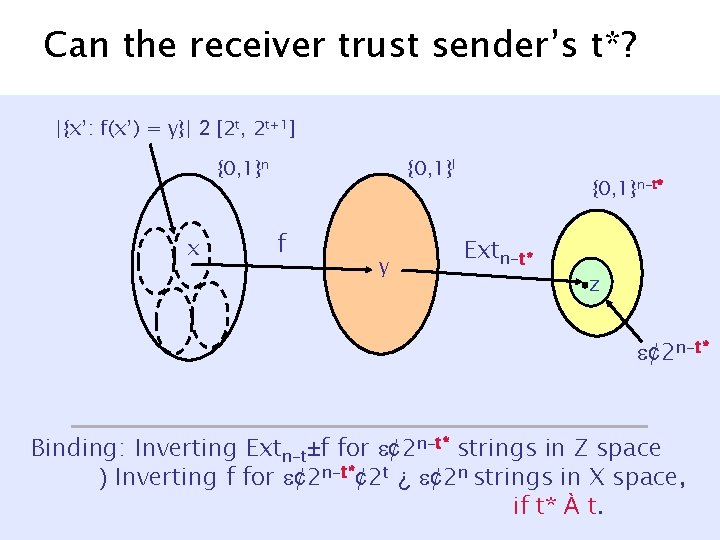
Can the receiver trust sender’s t*? |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n x {0, 1}l f y {0, 1}n-t* Extn-t* z ¢ 2 n-t* Binding: Inverting Extn-t±f for ¢ 2 n-t* strings in Z space ) Inverting f for ¢ 2 n-t*¢ 2 t ¿ ¢ 2 n strings in X space, if t* À t.

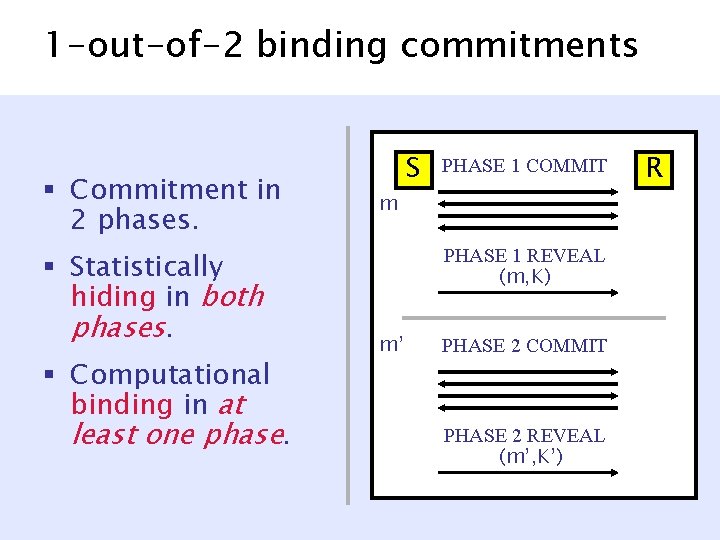
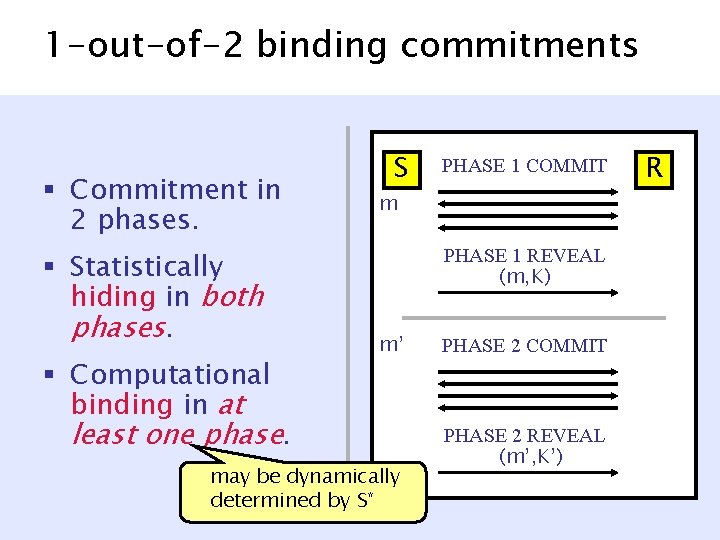
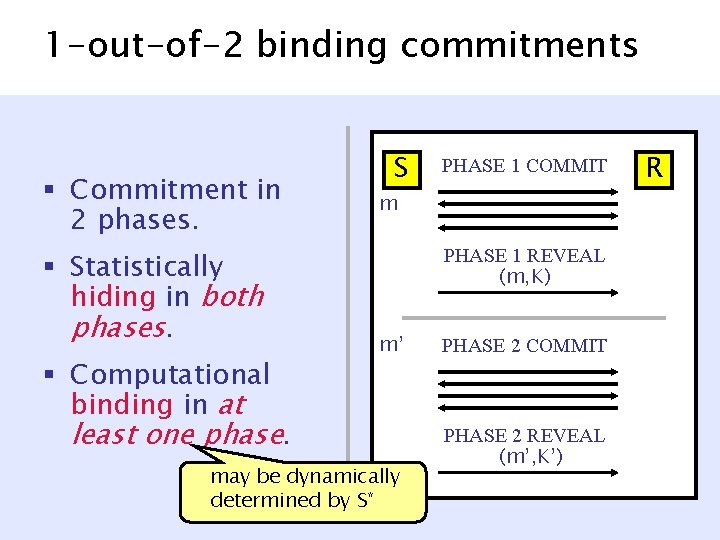
1 -out-of-2 binding commitments [Nguyen-Vadhan 06] § Commitment in 2 phases. § Statistically hiding in both phases. § Computational binding in at least one phase. S PHASE 1 COMMIT m PHASE 1 REVEAL (m, K) m’ may be dynamically determined by S* PHASE 2 COMMIT PHASE 2 REVEAL (m’, K’) R

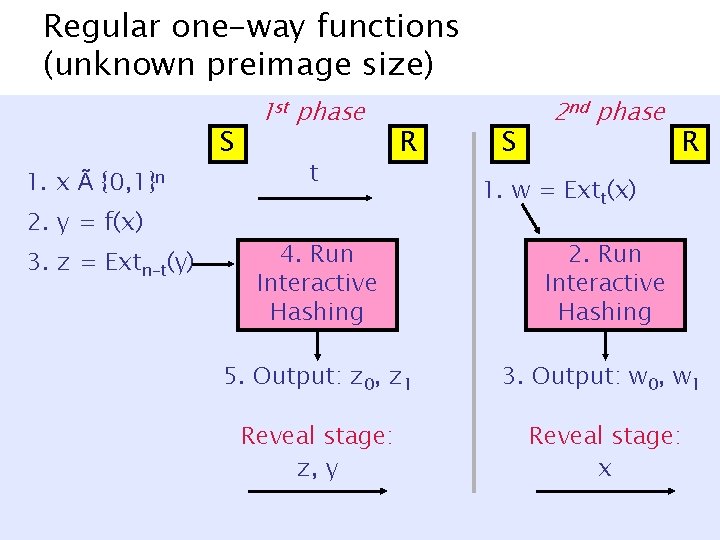
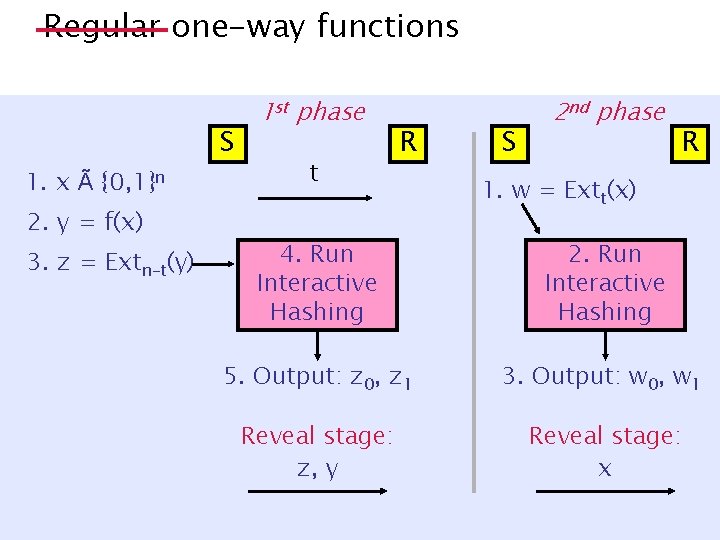
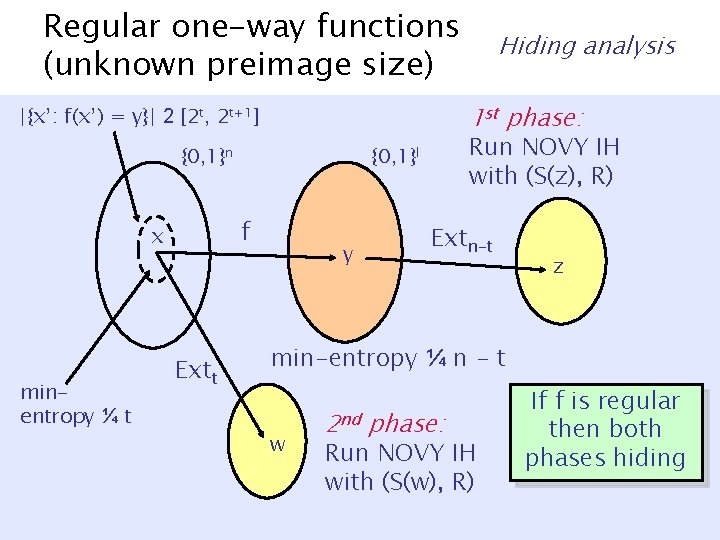
Regular one-way functions (unknown preimage size) S 1. x à {0, 1}n 2. y = f(x) 3. z = Extn-t(y) 1 st phase t R S 2 nd phase R 1. w = Extt(x) 4. Run Interactive Hashing 2. Run Interactive Hashing 5. Output: z 0, z 1 3. Output: w 0, w 1 Reveal stage: z, y Reveal stage: x

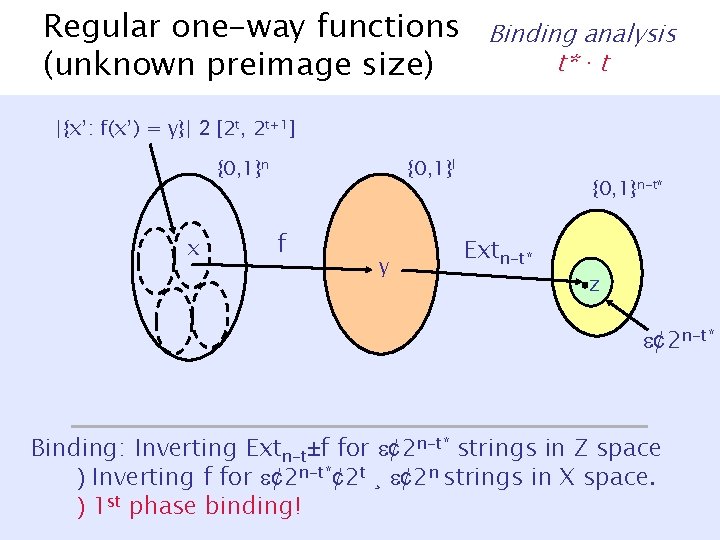
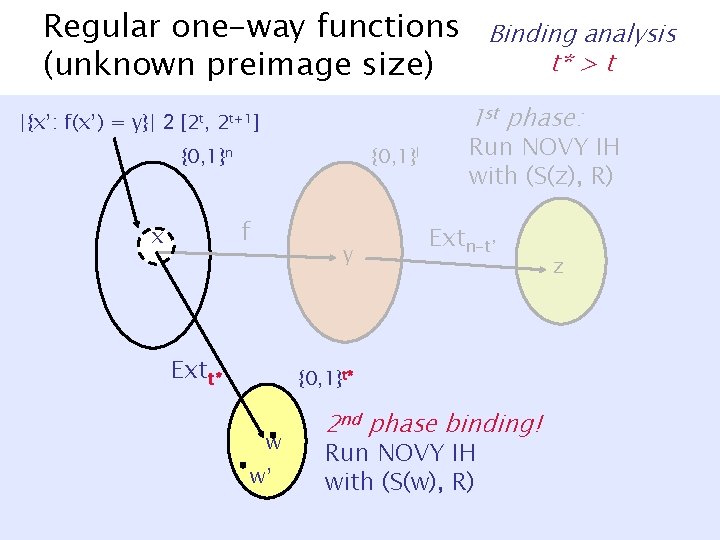
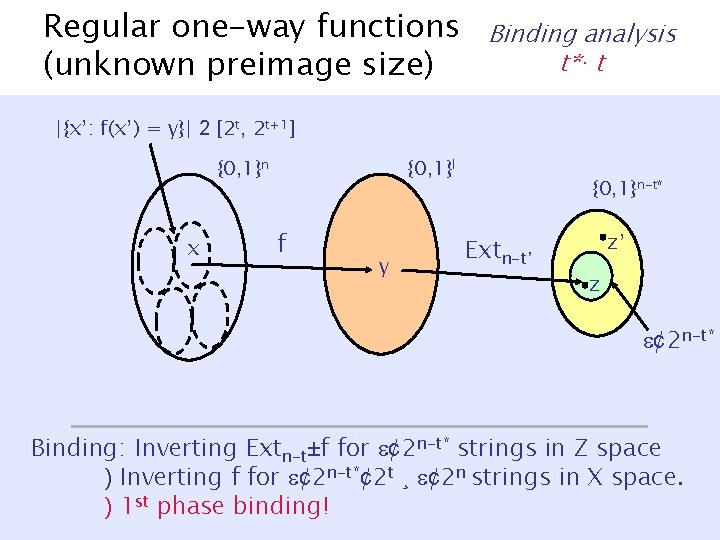
Regular one-way functions (unknown preimage size) Binding analysis t* · t |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n x {0, 1}l f y {0, 1}n-t* Extn-t* z ¢ 2 n-t* Binding: Inverting Extn-t±f for ¢ 2 n-t* strings in Z space ) Inverting f for ¢ 2 n-t*¢ 2 t ¸ ¢ 2 n strings in X space. ) 1 st phase binding!

Regular one-way functions (unknown preimage size) 1 st phase: |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n {0, 1}l f x Binding analysis t* > t y Extt* Run NOVY IH with (S(z), R) Extn-t’ {0, 1}t* w w’ 2 nd phase binding! Run NOVY IH with (S(w), R) z

1 -out-of-2 binding commitments § Commitment in 2 phases. § Statistically hiding in both phases. § Computational binding in at least one phase. m S PHASE 1 COMMIT PHASE 1 REVEAL (m, K) m’ PHASE 2 COMMIT PHASE 2 REVEAL (m’, K’) R

Regular one-way functions (unknown preimage size) S 1. x à {0, 1}n 2. y = f(x) 3. z = Extn-t(y) 1 st phase t R S 2 nd phase R 1. w = Extt(x) 4. Run Interactive Hashing 2. Run Interactive Hashing 5. Output: z 0, z 1 3. Output: w 0, w 1 Reveal stage: z, y Reveal stage: x

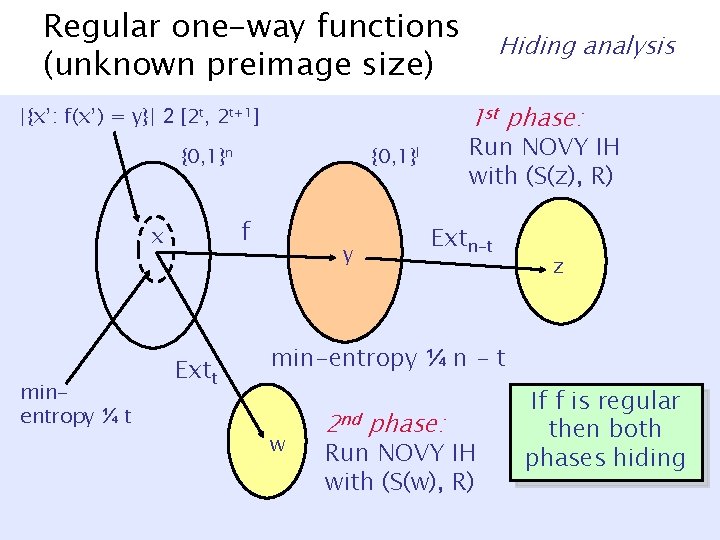
Regular one-way functions (unknown preimage size) 1 st phase: |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n minentropy ¼ t Extt Run NOVY IH with (S(z), R) {0, 1}l f x Hiding analysis y Extn-t z min-entropy ¼ n - t w 2 nd phase: Run NOVY IH with (S(w), R) If f is regular then both phases hiding

outline § Introduction § Commitments & ZK § Constructions from OWF with structure § Construction from any OWF § ZK ´ “Instance-Dependent” Commitments § Open Problems

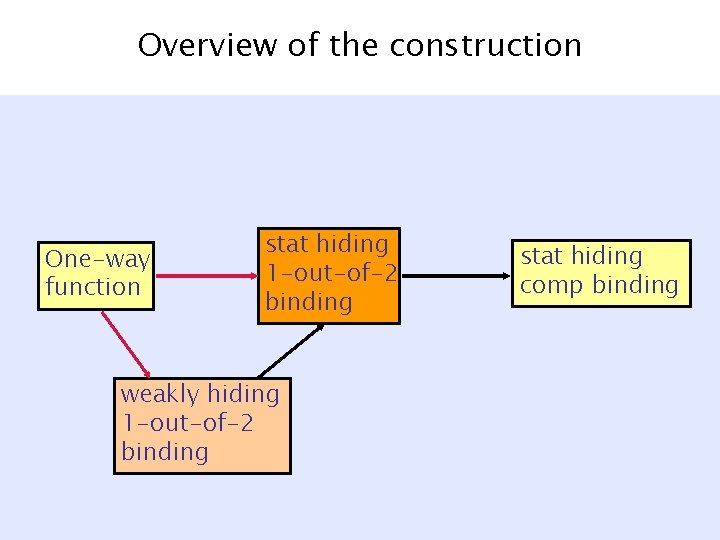
Overview of the construction One-way function stat hiding 1 -out-of-2 binding weakly hiding 1 -out-of-2 binding stat hiding comp binding

Regular one-way functions (unknown preimage size) S 1. x à {0, 1}n 2. y = f(x) 3. z = Extn-t(y) 1 st phase t R S 2 nd phase R 1. w = Extt(x) 4. Run Interactive Hashing 2. Run Interactive Hashing 5. Output: z 0, z 1 3. Output: w 0, w 1 Reveal stage: z, y Reveal stage: x

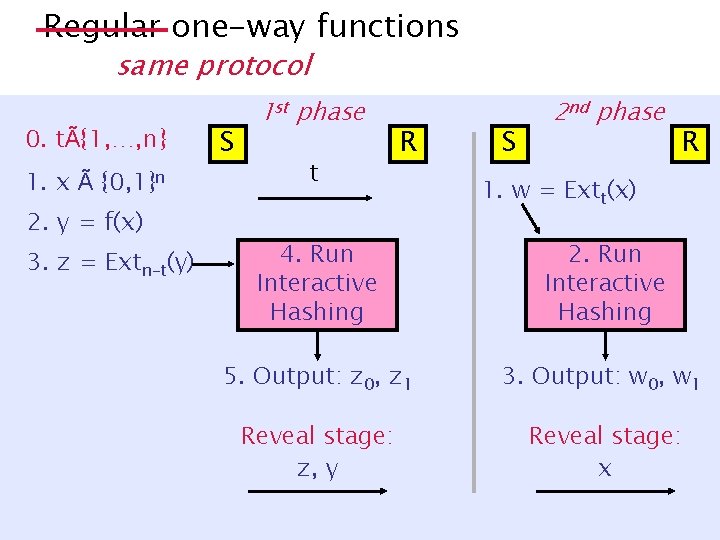
Regular one-way functions same protocol 0. tÃ{1, …, n} 1. x à {0, 1}n 2. y = f(x) 3. z = Extn-t(y) S 1 st phase t R S 2 nd phase R 1. w = Extt(x) 4. Run Interactive Hashing 2. Run Interactive Hashing 5. Output: z 0, z 1 3. Output: w 0, w 1 Reveal stage: z, y Reveal stage: x

Regular one-way functions (unknown preimage size) Binding analysis t*· t |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n x {0, 1}l f y {0, 1}n-t* Extn-t’ z’ z ¢ 2 n-t* Binding: Inverting Extn-t±f for ¢ 2 n-t* strings in Z space ) Inverting f for ¢ 2 n-t*¢ 2 t ¸ ¢ 2 n strings in X space. ) 1 st phase binding!

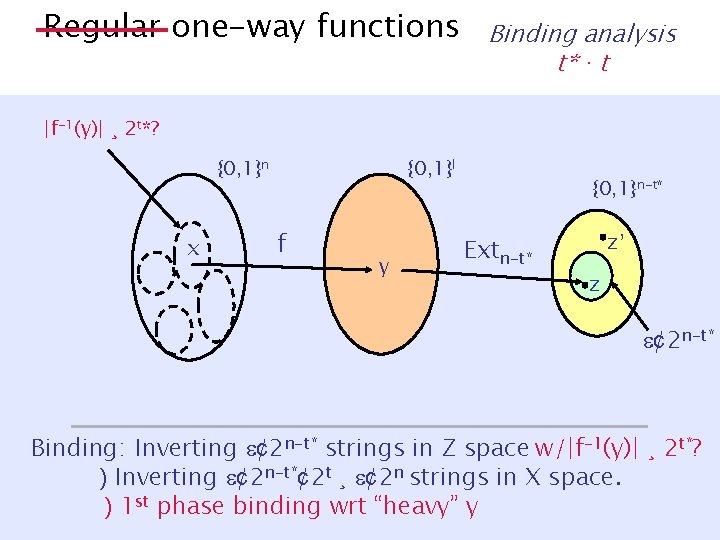
Regular one-way functions Binding analysis t* · t |f-1(y)| ¸ 2 t*? {0, 1}n x {0, 1}l f y {0, 1}n-t* Extn-t* z’ z ¢ 2 n-t* Binding: Inverting ¢ 2 n-t* strings in Z space w/|f-1(y)| ¸ 2 t*? ) Inverting ¢ 2 n-t*¢ 2 t ¸ ¢ 2 n strings in X space. ) 1 st phase binding wrt “heavy” y

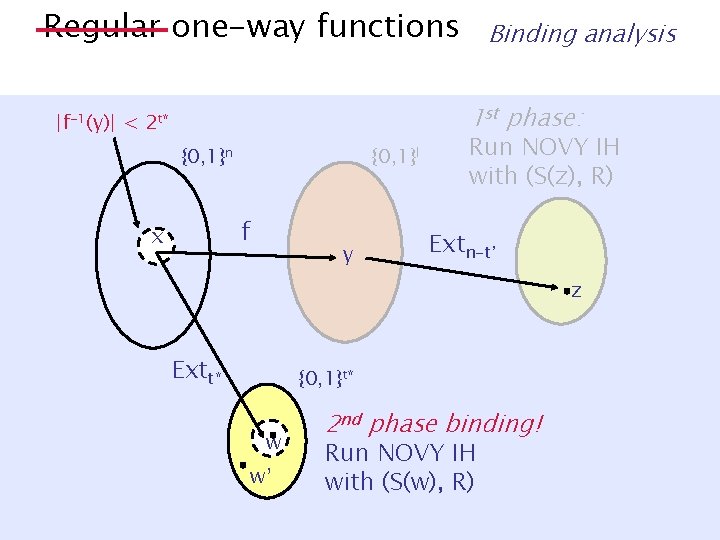
Regular one-way functions Binding analysis 1 st phase: |f-1(y)| < 2 t* {0, 1}n {0, 1}l f x y Run NOVY IH with (S(z), R) Extn-t’ z Extt* {0, 1}t* w w’ 2 nd phase binding! Run NOVY IH with (S(w), R)

1 -out-of-2 binding commitments § Commitment in 2 phases. § Statistically hiding in both phases. § Computational binding in at least one phase. S PHASE 1 COMMIT m PHASE 1 REVEAL (m, K) m’ may be dynamically determined by S* PHASE 2 COMMIT PHASE 2 REVEAL (m’, K’) R

Regular one-way functions (unknown preimage size) S 1. x à {0, 1}n 2. y = f(x) 3. z = Extn-t(y) 1 st phase t R S 2 nd phase R 1. w = Extt(x) 4. Run Interactive Hashing 2. Run Interactive Hashing 5. Output: z 0, z 1 3. Output: w 0, w 1 Reveal stage: z, y Reveal stage: x

Regular one-way functions (unknown preimage size) 1 st phase: |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n minentropy ¼ t Extt Run NOVY IH with (S(z), R) {0, 1}l f x Hiding analysis y Extn-t z min-entropy ¼ n - t w 2 nd phase: Run NOVY IH with (S(w), R) If f is regular then both phases hiding

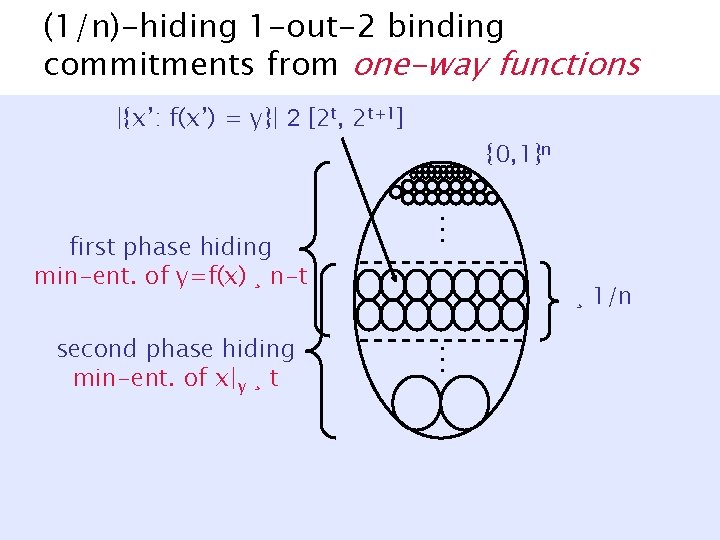
(1/n)-hiding 1 -out-2 binding commitments from one-way functions |{x’: f(x’) = y}| 2 [2 t, 2 t+1] ¸ 1/n … second phase hiding min-ent. of x|y ¸ t … first phase hiding min-ent. of y=f(x) ¸ n-t {0, 1}n

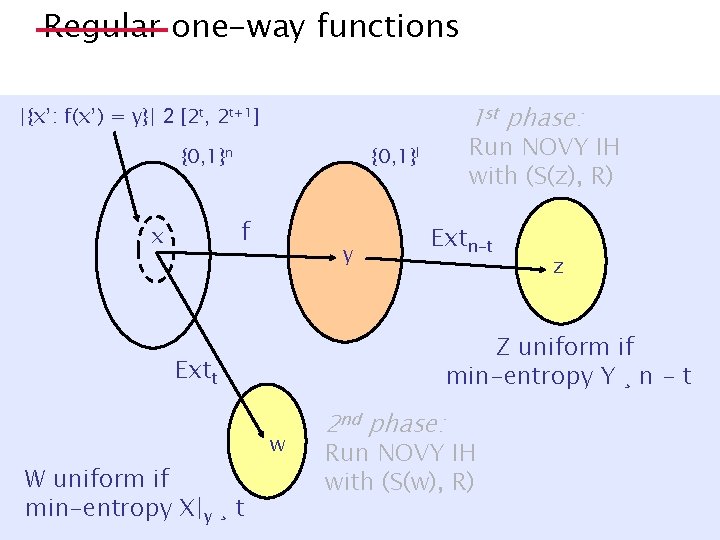
Regular one-way functions (unknown preimage size) 1 st phase: |{x’: f(x’) = y}| 2 [2 t, 2 t+1] {0, 1}n f x Run NOVY IH with (S(z), R) {0, 1}l y Extn-t Z uniform if min-entropy Y ¸ n - t Extt w W uniform if min-entropy X|y ¸ t z 2 nd phase: Run NOVY IH with (S(w), R)

Overview of the construction UOWHF [Rompel 90] One-way function stat hiding 1 -out-of-2 binding (1/n)-hiding 1 -out-of-2 binding stat hiding comp binding

(1/n)-hiding ) (1)-hiding § Amplify in O(log n) stages – Each time -hiding 2 -hiding – Inspired by [Reingold 05, Dinur 06] § Each Stage – O(1) repetitions of protocol. – Combine using interactive hashing [OVY, CCM, DHRS]. – Lose O(1) bits in message length. • Nonstandard measures of hiding & binding quality. • Start & end with O(log n)-bit messages.

(1)-hiding ) statistically hiding § Amplify in 1 more stage § Each Stage – poly(n) repetitions of protocol. – Combine using interactive hashing. – Gain poly(n) bits in message length. • Standard measures of hiding & binding quality. • End with poly(n)-bit messages.

Overview of the construction One-way function stat hiding 1 -out-of-2 binding (1/n)-hiding 1 -out-of-2 binding stat hiding comp binding

Overview of the construction UOWHF [Rompel 90] One-way function stat hiding 1 -out-of-2 binding (1/n)-hiding 1 -out-of-2 binding © stat hiding comp binding

1 -out-of-2 binding commitments § Commitment in 2 phases. § Statistically hiding in both phases. § Computational binding in at least one phase. S PHASE 1 COMMIT m PHASE 1 REVEAL (m, K) m’ may be dynamically determined by S* PHASE 2 COMMIT PHASE 2 REVEAL (m’, K’) R

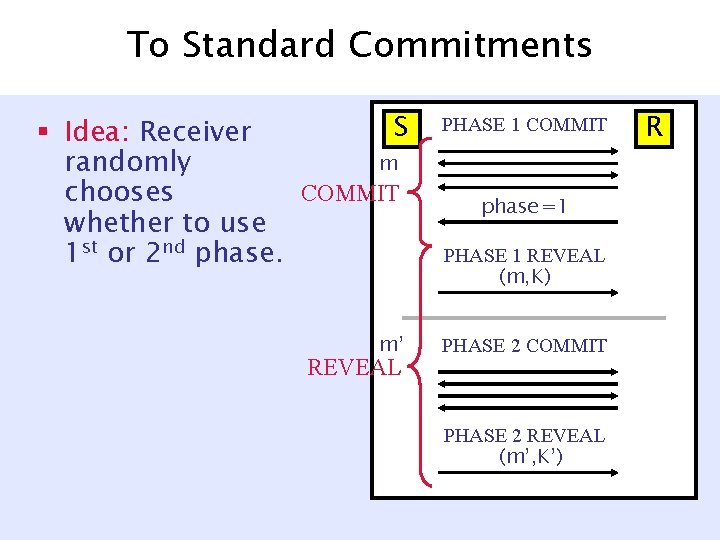
To Standard Commitments S § Idea: Receiver m randomly COMMIT chooses whether to use 1 st or 2 nd phase. PHASE 1 COMMIT m’ PHASE 2 COMMIT REVEAL phase =1 PHASE 1 REVEAL (m, K) PHASE 2 REVEAL (m’, K’) R

To Standard Commitments § Idea: Receiver randomly chooses whether to use 1 st or 2 nd phase. S PHASE 1 COMMIT m phase =2 COMMIT § Problem: Sender m’ may decide which phase to break after choice of phase. REVEAL PHASE 1 REVEAL (m, K) PHASE 2 COMMIT PHASE 2 REVEAL (m’, K’) R

To Standard Commitments § Fix: Have sender provide a “collisionresistant” hash of m S m – Determines m (computationally). – Enough entropy left in m to extract a random secret. – At most one value of m allows breaking Phase 2 binding. ) only need UOWHF PHASE 1 COMMIT h h(m) phase (m, K) m’ PHASE 2 COMMIT PHASE 2 REVEAL (m’, K’) R

Overview of the construction UOWHF [Rompel 90] One-way function stat hiding 1 -out-of-2 binding (1/n)-hiding 1 -out-of-2 binding © stat hiding comp binding

outline § Introduction § Commitments & ZK § Constructions from OWF with structure § Construction from any OWF § ZK ´ “Instance-Dependent” Commitments § Open Problems

Instance-Dependent Commitments Thm [OV 07]: For every L 2 NP, L has ZK protocol iff L has i. d. commitments [IOS 94]. x (S, R) s. t. x 2 L ) (S, R) hiding x L ) (S, R) binding Moreover, stat/comp ZK $ stat/comp hiding proof/argument $ stat/comp binding Previously partial results [D 89, D 93, O 91, OW 93, MV 03, V 04, NV 06, KMS 07]

Instance-Dependent Commitments Thm [OV]: For every L 2 NP, L has ZK protocol iff L has i. d. commitments. stat/comp ZK $ stat/comp hiding proof/argument $ stat/comp binding Proof overview ()): § 9 characterizations of all 4 ZK classes in terms of SZKP and “i. d. OWFs” [V 04, OV 07]. § i. d. OWFs ) i. d. commitments [HILL 90, N 91, NOV 06, HR 07]. § SZKP i. d. commitments by combining – i. d. 1 -out-of-2 binding commitments [NV 06] – i. d. UOWHFs [OV]

Open Problems § Simplify the construction. § Better (sub-polynomial) round complexity. – Requires non-black-box construction, even for one-way permutations [HHRS 07]. § Complexity of other crypto primitives. – Noninteractive zero knowledge for NP. – Chosen-ciphertext secure encryption.

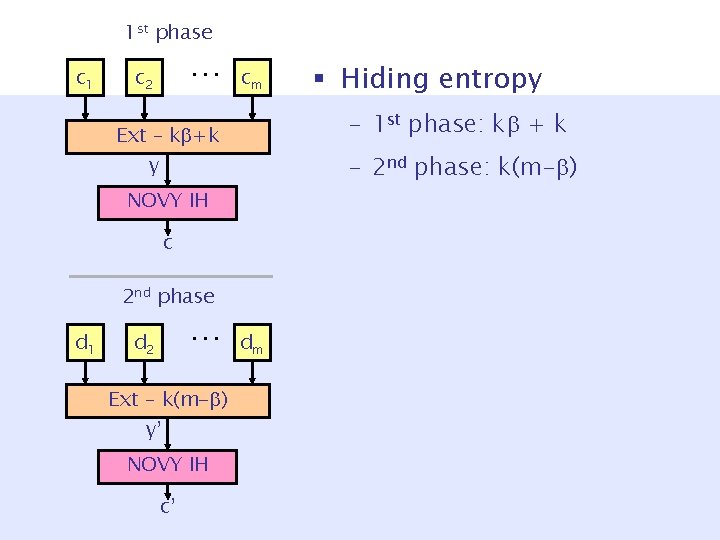
Pr[both phases hiding] = = 1/n c 1 1 st phase commitment d 1 2 nd phase commitment c 1 & d 1 are both k-bit strings Properties: 1. Either first or second phase hiding. 2. Both phases stat. hiding w. p. ¸ . 3. 1 -out-2 comp. binding.

Pr[both phases hiding] = = 1/n hiding entropy k( + 1) = k + k + 1 hiding in 1 st phase c 1 c 2 … cm ci & di are k-bit strings k(m - ) d 1 d 2 … dm m - hiding in 2 nd phase Pr[( +1) 1 st hiding & (m- ) 2 nd hiding] ¼ m ¢ (m-½) = (m½ ) > 2 , for m large enough constant.

1 st phase c 1 … c 2 cm – 1 st phase: k + k Ext – k +k y – 2 nd phase: k(m- ) NOVY IH c 2 nd phase d 1 … d 2 Ext – k(m- ) y’ NOVY IH c’ § Hiding entropy dm

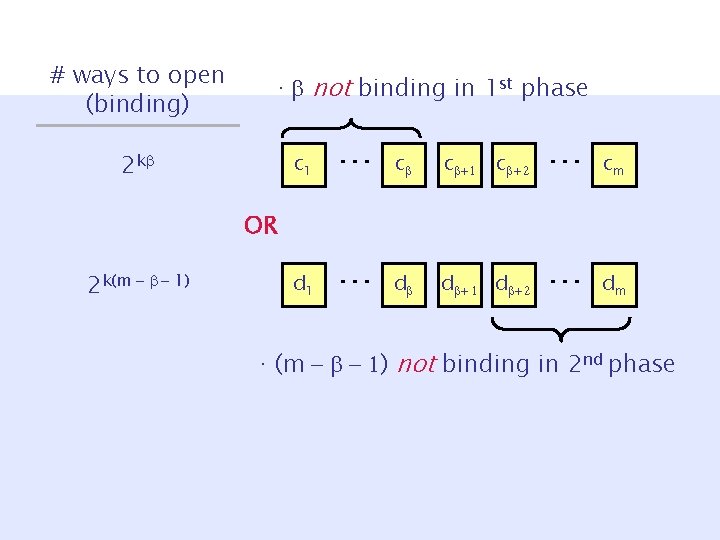
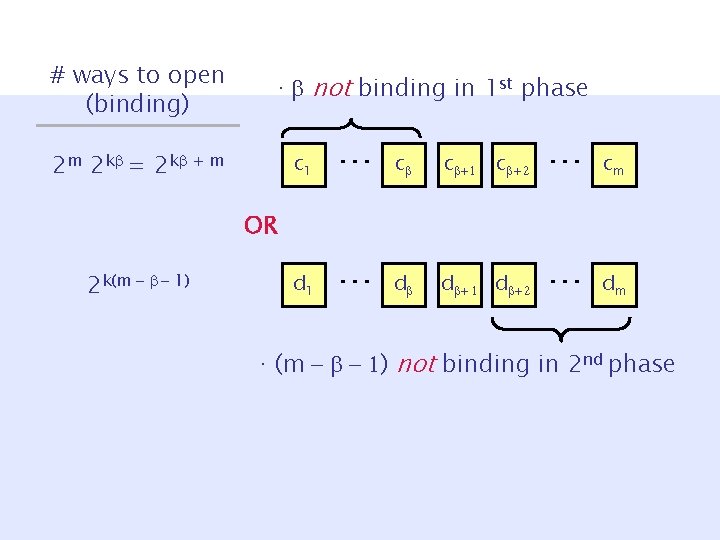
# ways to open (binding) · not binding in 1 st phase 2 k c 1 … c c +1 c + 2 … cm d 1 … d d + 1 d + 2 … dm OR 2 k(m - - 1) · (m - - 1) not binding in 2 nd phase

# ways to open (binding) · not binding in 1 st phase 2 m 2 k = 2 k + m c 1 … c c +1 c + 2 … cm d 1 … d d + 1 d + 2 … dm OR 2 k(m - - 1) · (m - - 1) not binding in 2 nd phase

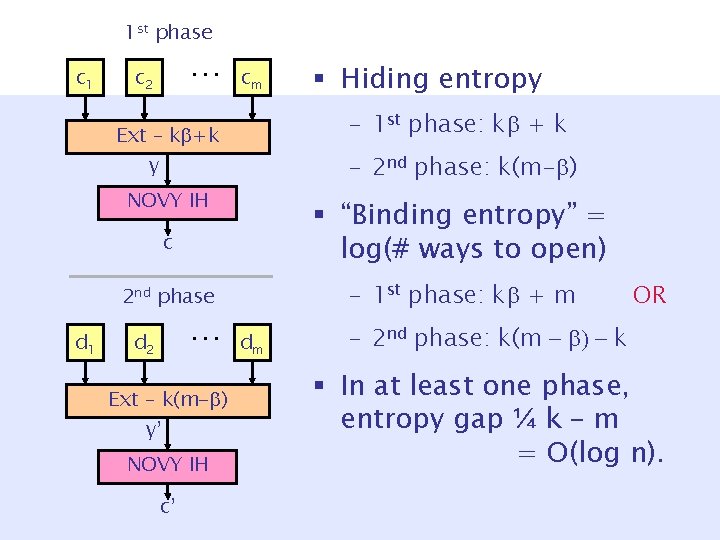
1 st phase c 1 … c 2 cm – 1 st phase: k + k Ext – k +k y – 2 nd phase: k(m- ) NOVY IH § “Binding entropy” = log(# ways to open) c – 1 st phase: k + m 2 nd phase d 1 … d 2 Ext – k(m- ) y’ NOVY IH c’ § Hiding entropy dm OR – 2 nd phase: k(m - ) - k § In at least one phase, entropy gap ¼ k – m = O(log n).

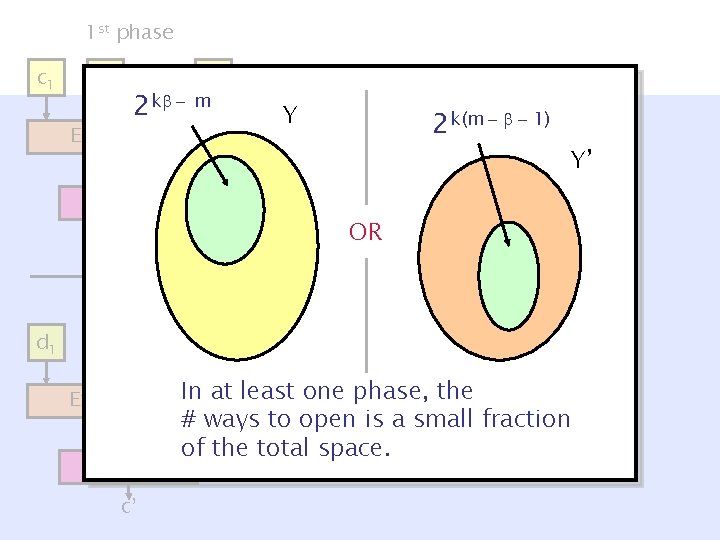
1 st phase c 1 c 2 … cm 2 k - m Ext – k( +1) y § Hiding entropy c d 1 § # ways to open (binding) phase … d 2 Y’ – 1 st phase: k( +1) – 2 nd. OR phase: k(m- ) NOVY IH 2 nd Pr[( +1) 1 st phase hiding & Y(m- ) 2 nd phase 1) 2 k(m - -hiding] dm – 1 st phase: 2 m 2 k ’=2 k( ’ - m/k) – 2 nd phase: 2 k(m- ’) § In at least one phase, Ext – k(m- )In at least one phase, the ¼fraction k–m # ways toentropy open is agap small y’ NOVY IH c’ of the total space. = O(log n).

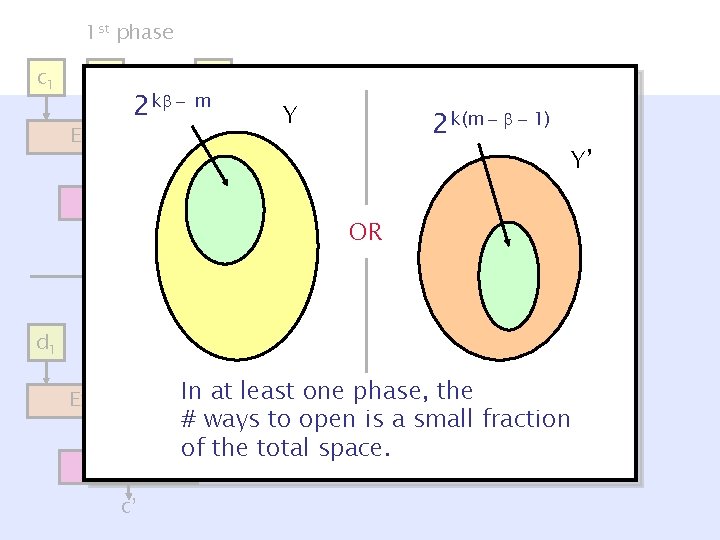
1 st phase c 1 c 2 … cm 2 k - m Ext – k( +1) y § Hiding entropy c d 1 § # ways to open (binding) phase … d 2 Y’ – 1 st phase: k( +1) – 2 nd. OR phase: k(m- ) NOVY IH 2 nd Pr[( +1) 1 st phase hiding & Y(m- ) 2 nd phase 1) 2 k(m - -hiding] dm – 1 st phase: 2 m 2 k ’=2 k( ’ - m/k) – 2 nd phase: 2 k(m- ’) § In at least one phase, Ext – k(m- )In at least one phase, the ¼fraction k–m # ways toentropy open is agap small y’ NOVY IH c’ of the total space. = O(log n).